基于膜计算和粒子群的煤矿移动机器人动态窗口算法研究
兰世豪,韩涛,黄友锐,徐善永
(安徽理工大学 电气与信息工程学院, 安徽 淮南 232000)
0 引言
随着煤矿开采智能化、无人化的发展,煤矿移动机器人在煤矿运输、救援、勘测等方面得到了快速发展[1]。良好的自主导航技术是煤矿移动机器人在煤矿复杂、未知环境中正常工作的保障,而自主导航技术的研究与路径规划算法的研究密不可分,局部路径规划算法是应对复杂动态环境的良好解决办法[2]。
经典的局部路径规划算法有bug避障算法[3]、人工势场法[4]、增强向量场直方图法[5-6]等,它们在简单环境中可以实时避开障碍物,但面对狭长走廊或密集障碍物时,算法会出现抖动或陷入局部极值,导致规划路径不合理和安全度降低。且以上算法规划出路径后,需根据规划好的路径计算移动机器人行驶的速度,才能用于实际移动机器人运动,不能直接产生移动机器人行驶所需的速度。为此,D.Fox等[7]提出了动态窗口算法(Dynamic Window Algorithm,DWA),该算法在考虑机器人动力学约束和环境因素的基础上,直接产生一组机器人下一时刻行驶的避障速度,但是在复杂环境中要输出准确最优速度,需要对速度空间进行多组均匀等分采样并评价比较,这就导致算法评价的速度过慢且无法产生最优速度。P. Saranrittichai等[8]提出了区域动态窗口算法,将算法模拟轨迹上的障碍物扩大到临近轨迹,增加了机器人搜索附近障碍物的能力,避免了机器人撞到一些靠近轨迹但不在轨迹上的障碍物,该算法具有良好的鲁棒性,但难以解决面对复杂障碍物时规划路径实时性差的问题。A. Maroti等[9]提出了一种考虑机器人自身尺寸和U型障碍物开口宽度关系的改进动态窗口算法,在一定程度上解决了局部极小值问题,但在机器人行驶速度过快时,算法不能及时输出最优速度,导致机器人易陷入U型障碍物内。王永雄等[10]提出了自适应参数动态窗口算法,算法评价函数中的速度权值可随环境自适应变化,以使机器人获取最佳的运动速度,有效提升了算法的评价速度和机器人穿越复杂环境的能力,但在复杂环境中,机器人自身速度过快时,规划轨迹的速度相对较慢,甚至会出现绕行或碰撞[11]。
针对上述问题,本文提出了一种基于膜计算(Membrane Computing,MC)和粒子群(Particle Swarm Optimization,PSO)的煤矿移动机器人动态窗口算法(MCPSO-DWA)。该算法将DWA中煤矿移动机器人的速度限制空间转换为坐标空间,将煤矿移动机器人的速度坐标看作粒子位置,利用粒子群算法将速度空间从均匀等分采样变为随机采样,减少采样速度的组数,再利用膜计算的膜内更新和膜间交流规则对粒子群进行优化,加快种群寻优速度。利用DWA中的适应度函数对采样的粒子进行评价并比较,根据种群最优和每个粒子的历史最优更新粒子位置和速度[12-14],当种群迭代次数或粒子适应度值达到一定条件时,输出粒子位置,即煤矿移动机器人下一时刻最佳运动速度,从而使煤矿移动机器人面对复杂环境时能快速规划出更加合理的路径。
1 基于膜计算的粒子群算法
1.1 粒子群算法
粒子群(PSO)算法是一种基于群体协作的随机搜索算法,通过粒子间的不断协作和种群迭代来寻找最优解。每个粒子根据自身的位置和相应的适应度函数来评价自身的适应度值,根据粒子的适应度值来确定每个粒子的历史最优位置和种群最优的粒子位置,并利用它们来更新粒子位置和速度[15]。更新后粒子的位置和速度如下:
(1)
(2)
式中:xie(n+1)和xie(n)分别为种群在第n+1次和第n次迭代时第i个粒子在e维的位置;vie(n+1)和vie(n)分别为种群在第n+1次和第n次迭代中第i个粒子在e维的速度;w为惯性权重[16],wmin和wmax分别为惯性权重的最小值和最大值,N为最大迭代次数;c1和c2为学习因子;r1和r2为[0,1]之间的随机数;pie(n)和pge(n)分别为种群第n次迭代时第i个粒子在e维的历史最优位置和种群在e维上的历史最优位置。
1.2 基于膜计算的粒子群算法


图1 MCPSO工作流程Fig.1 Work flow of MCPSO
基于膜计算的并行计算能力,m个基本膜内的粒子同时进行搜索并产生各基本膜内的全局最优,再通过比较得到种群的全局最优。基于膜计算的粒子群算法可以在保证粒子寻优精度的同时提高种群寻优速度。
2 基于膜计算和粒子群的动态窗口算法
2.1 传统动态窗口算法
传统动态窗口算法(DWA)是根据煤矿移动机器人在环境中的位置和自身速度约束,将煤矿移动机器人的局部轨迹规划转换为速度选择问题,选取煤矿移动机器人最优轨迹对应的速度来驱动机器人做下一时刻的运动[20-21]。
煤矿移动机器人先根据自身速度和环境的约束对自身采样速度进行一定的限制。煤矿移动机器人的速度限制用速度集表示为
Va={(v,ω)|0≤v≤vmax,-ωmax≤ω≤ωmax}
(3)
式中:v,ω分别为煤矿移动机器人的线速度和角速度;vmax,ωmax分别为煤矿移动机器人的最大线速度和角速度。
受电动机力矩影响,煤矿移动机器人存在最大加减速度,所以,在固定时间间隔θt内,煤矿移动机器人允许的最大速度变化范围为
(4)

考虑煤矿移动机器人的安全性,在以最大加减速度下进行速度变化行驶过程中,煤矿移动机器人要与障碍物保持安全的距离。要让煤矿移动机器人在碰撞到障碍物之前停止运动,其速度必须在一定的范围内。
(5)
式中dist(v,ω)为煤矿移动机器人当前模拟轨迹与障碍物之间的距离。
最终煤矿移动机器人的行驶速度集合为
Vf=Va∩Vg∩Vz
(6)
速度采样后,对速度空间以固定的步进进行速度采样,并对采样的速度进行评价,评价函数为
H(v,ω)=α×heading(v,ω)+β×dist(v,ω)+γ×velocity(v,ω)
(7)
式中:heading(v,ω)为煤矿移动机器人以当前采样速度行驶到达模拟轨迹末端时的煤矿移动机器人朝向与目标点之间的角度差;velocity(v,ω)为采样速度中的线速度;α,β,γ为3个权值参数,评价速度之前先将目标函数的3个参数归一化处理为[0,1]之间的参数,避免某个参数权重较大而影响速度的评价质量。
通过评价函数H(α=0.4,β=0.2,γ=0.4)对机器人的速度空间[(0,2)m/s;(-50,50)rad/s]以步进(0.01 m/s,0.2 rad/s)进行评价和比较,最大H值对应的(v,ω)即为煤矿移动机器人下一时刻行驶的线速度和角速度。基于DWA的煤矿移动机器人运动轨迹如图2所示,图中黑色正方形和圆形为经过膨化后的障碍物。
从图2可看出,煤矿移动机器人在面对复杂稠密障碍物时无法穿越并出现了绕行情况,增加了煤矿移动机器人的总行驶路程。

图2 基于DWA的煤矿移动机器人运动轨迹Fig.2 Mine mobile robot trajectory based on DWA
2.2 基于膜计算和粒子群的动态窗口算法
DWA在复杂环境中规划路径不合理,规划效率低,其原因为算法评价函数对其速度采样空间评价的速度太慢,无法及时产生最优速度,导致煤矿移动机器人穿越稠密障碍物时规划路径不合理。为此,本文提出了基于膜计算和粒子群的动态窗口算法(MCPSO-DWA),利用MCPSO对DWA中速度空间进行采样并评价,最终得出煤矿移动机器人下一时刻行驶的最优速度。
2.2.1 算法设计
将煤矿移动机器人的速度限制区域Vf转换为坐标区域,以v和ω为横坐标和纵坐标建立坐标系,如图3所示,其中(vmin,vmax)和(-ωmax,ωmax)分别为煤矿移动机器人的限制速度范围,阴影部分S为煤矿移动机器人的速度限制区域。将S转换为粒子群算法中粒子的搜索区域,其中(vmin,vmax)和(-ωmax,ωmax)为粒子搜索边界,将S中坐标点(v,ω)转换为粒子对应的位置X。粒子在S中不断更新位置和速度,最终输出最优粒子对应的位置(v,ω),即MCPSO-DWA输出的最优行驶速度。

图3 速度限制区域坐标Fig.3 Coordinate of speed limit area
初始化一个单层膜结构,其中包括1个表层膜和m个基本膜。在区域S中,初始化选取Q个粒子,每个粒子的位置代表机器人的一个速度位置坐标,粒子位置和速度的初始化公式为
X=[(vmax,ωmax)-(vmin,-ωmax)]×r+(vmin,ωmax)
(8)
V=[(vmax,ωmax)-(vmin,ωmax)]×0.1×(2r-1)
(9)
式中:X和V分别为粒子初始位置和速度;r为[0,1]之间的随机数。
将Q个粒子均匀分配到m个基本膜当中,每个基本膜内含有D个粒子,第k(k=1,2,…,m)个基本膜内的第d(d=1,2,…,D)个粒子的初始速度为Vkd,初始位置为Xkd。利用评价函数(式(7))对各基本膜内的粒子进行评价,根据每个粒子对应评价函数的得分比较得出每个基本膜内的全局最优,将各基本膜内全局最优对应的粒子输出到表层膜中进行比较,得到种群全局最优,各基本膜内粒子根据表层膜返回的种群全局最优和自身历史最优进行位置和速度的更新,整个种群不断迭代更新,直到种群输出最优粒子的位置,即煤矿移动机器人下一时刻的行驶速度。煤矿移动机器人不断根据单位采样周期内输出的最优速度进行行驶,并判断是否到达终点。
2.2.2 算法流程
MCPSO-DWA流程如图4所示。
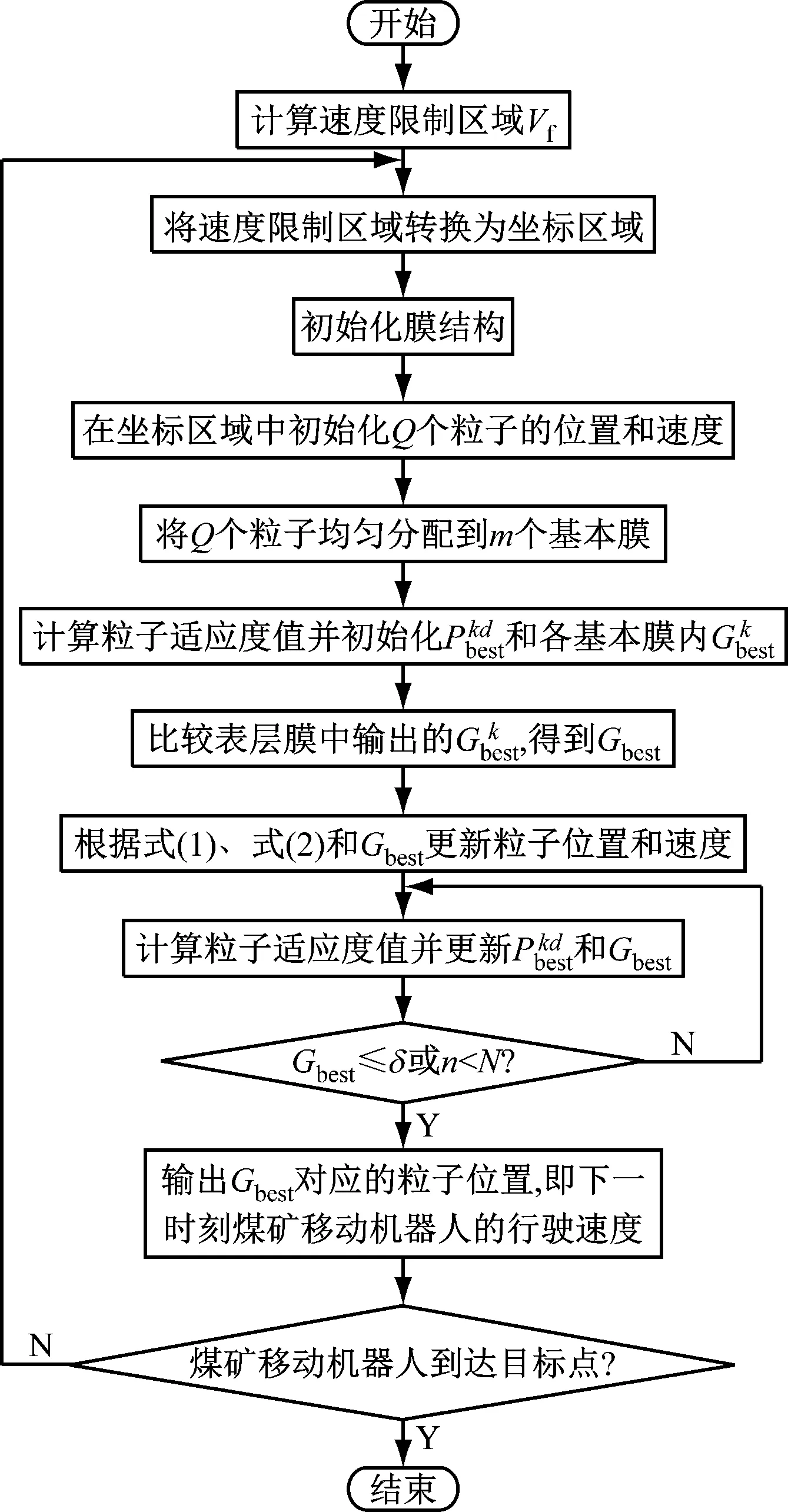
图4 MCPSO-DWA流程Fig.4 MCPSO-DWA flow
(1) 根据煤矿移动机器人自身动力学约束和传感器接收的环境信息产生煤矿移动机器人的速度限制区域Vf。
(2) 将速度限制区域Vf转换为坐标区域。
(3) 初始化单层膜结构,其结构包括1个表层膜和m个基本膜;在速度限制区域Vf中随机选取Q个粒子,根据式(8)和式(9)产生粒子的位置和速度,并均匀分配到m个基本膜中,表层膜为空;设定学习因子c1,c2和惯性权重wmin,wmax,最大迭代次数N,适应度函数阈值δ。

(8) 膜内种群不断迭代更新,直到达到最大迭代次数或者种群全局最优Gbest的适应度值达到δ,停止迭代,输出此时Gbest对应粒子的位置坐标,即煤矿移动机器人下一时刻行驶的避障速度,否则返回步骤(3)。
(9) 执行输出的避障速度,并判断煤矿移动机器人是否达到目标点,若达到,则停止煤矿移动机器人运动,否则返回步骤(1),继续搜索下一时刻的最优避障速度,直到达到终点。
2.2.3 算法应用
MCPSO-DWA改进了传统DWA速度空间中速度的采样方式,利用MCPSO变均匀等分采样为随机采样,将采样的速度模拟为煤矿移动机器人下一时刻的行驶轨迹,再结合煤矿移动机器人接收到的复杂环境信息,对每条模拟轨迹进行评价,多次迭代并产生煤矿移动机器人下一时刻行驶的最优速度。要达到煤矿移动机器人根据连续时间段间隔内输出的最优速度进行路径规划,就要求算法在固定时间间隔内及时产生煤矿移动机器人下一时刻的最优行驶速度,煤矿移动机器人用最优速度行驶,并按固定时间间隔进行一次最优行驶速度的更新,使煤矿移动机器人在连续时间间隔内都可以采用最优速度行驶,实现实时的局部避障规划,以保证煤矿移动机器人在煤矿复杂多变的环境中安全高效行驶。
3 实验结果及分析
为验证MCPSO-DWA的有效性,分别在不同复杂度的环境中,对比MCPSO-DWA和DWA的性能,对煤矿移动机器人行驶的路程、时间和穿越密集障碍物的能力等进行比较和分析。
3.1 实验参数设定
利用Python 3.7进行实验仿真,构建的基本地图如图2所示,在此基础上验证煤矿移动机器人遇到障碍物时规划路径的能力。
MCPSO-DWA的相关参数配置见表1,在速度坐标区域中共选取20个粒子,并均匀分配到4个基本膜中。根据煤矿移动机器人的实际情况配置DWA参数,见表2,对障碍物进行半径为0.5 m的膨化处理。

表1 MCPSO-DWA参数配置Table 1 Parameters configuration of MCPSO-DWA

表2 DWA参数配置Table 2 Parameters configuration of DWA
3.2 仿真实验与分析
为验证MCPSO-DWA在不同场景的适应能力,先在4种不同复杂度环境的地图上对算法性能进行验证,4种环境的复杂度依次增加,在环境3和环境4中,障碍物密集度不断提升。煤矿移动机器人在4种环境中利用DWA和MCPSO-DWA规划的最优路径对比如图5所示;煤矿移动机器人在4种环境中按照MCPSO-DWA和DWA规划路径行驶时的总步数与每步评价次数对比如图6所示。MCPSO-DWA运行步数和每步迭代次数的关系如图7所示。
从图5(a)、图5(b)可看出,在环境1和环境2中,DWA和MCPSO-DWA都可以穿越障碍物,规划出比较合理路径。从图6(a)、图6(b)可看出,在环境1和环境2中规划路径时,DWA迭代的总步数分别为58和75,由表2中DWA相关参数所决定,故每步对应评价次数均为800;在环境1和环境2中规划路径时,MCPSO-DWA迭代的总步数分别为64和70,每步对应评价次数为种群在速度坐标区域迭代搜索时,当种群中Gbest的值达到要求阈值,种群所迭代的次数n乘以粒子数Q的值。从图7可看出MCPSO-DWA运行步数和每步迭代次数的关系,其中由环境1和环境2对应折线可得MCPSO-DWA运行每步的迭代次数为5~30,结合图6(a)和6(b)可看出,每步评价次数为100~600,
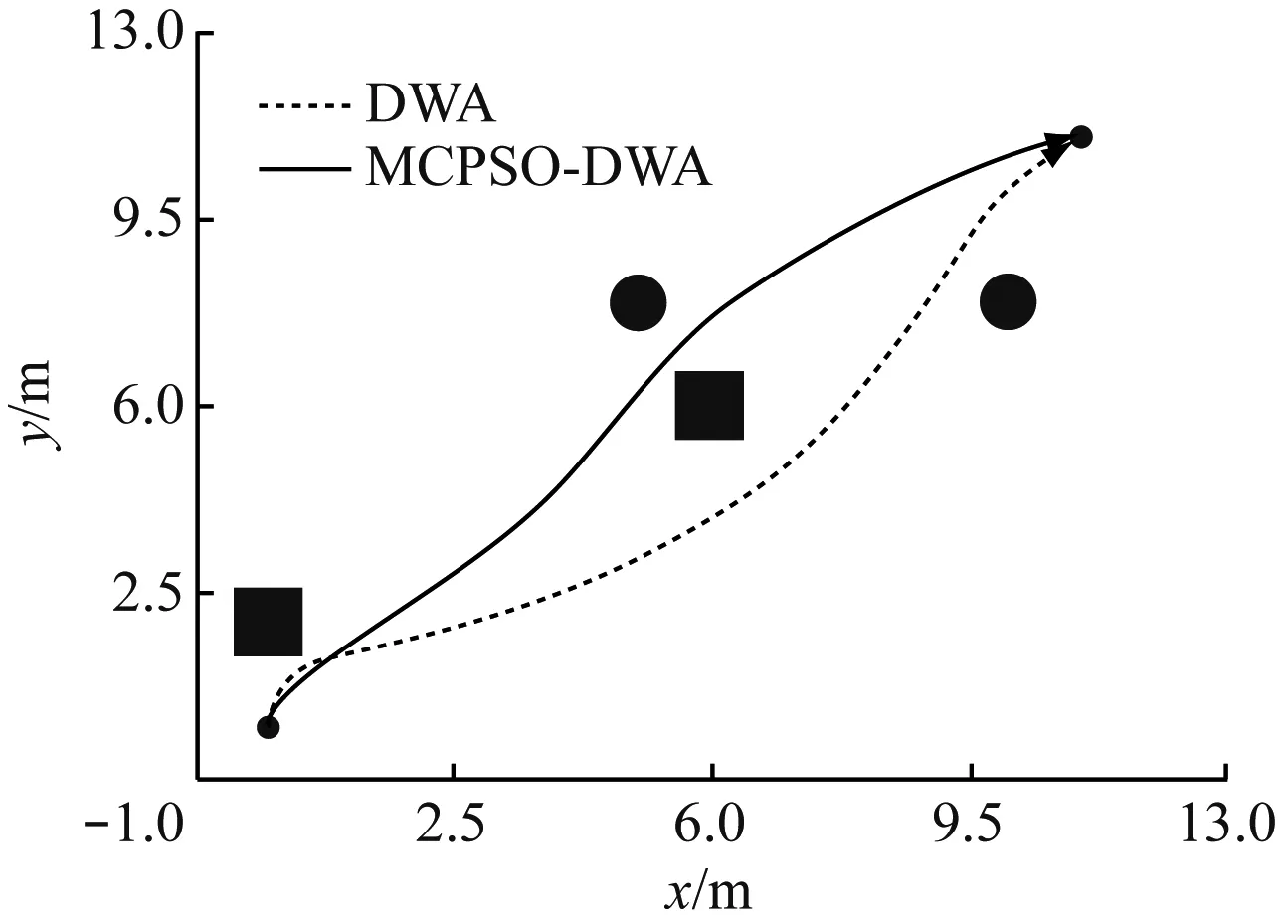
(a) 环境1中2种算法规划路径对比

(a) 环境1中2种算法规划步数与评价次数对比
低于DWA每步评价次数。从图5(c)和图5(d)可看出, MCPSO-DWA规划出的路径明显比DWA规划出的路径更加合理,面对稠密障碍物, MCPSO-DWA规划的路径可以安全穿越;从图6(c)和图6(d)可看出,MCPSO-DWA迭代总步数分别为76和124,也分别少于DWA迭代总步数83和165。同时从图7中的环境3、环境4对应折线和图6(c)、图6(d)可看出, MCPSO-DWA运行每步的迭代次数为10~35,每步评价次数为200~700,也均少于DWA每步800次的评价次数。

图7 MCPSO-DWA规划步数与每步迭代次数的关系Fig.7 Relationship between the number of planning steps and the number of iterations per step of MCPSO-DWA
表3给出了DWA和MCPSO-DWA在以上环境中规划路径的数据对比。从表3可看出,对于简单的环境1, MCPSO-DWA规划路径的时间和总步数虽然不占优势,但规划路径的长度比DWA要短8.77%;对于一般复杂度的环境2和环境3, MCPSO-DWA规划路径用时分别比DWA规划路径用时要少8.66%和15.53%,并且规划路径的长度也比DWA规划路径长度短2.30%和6.71%;对于复杂环境4, MCPSO-DWA相比DWA在总步数减少41步的情况下,规划时间减少31.55%,规划路径长度减少10.02%。
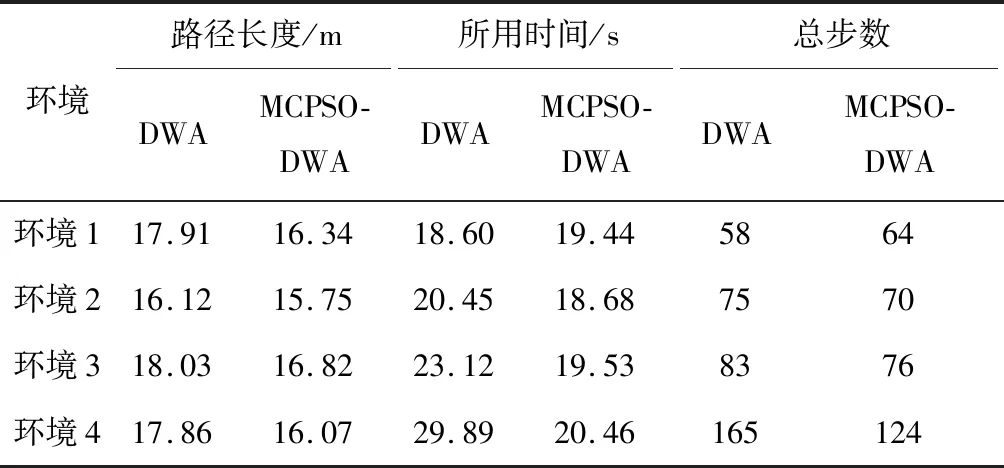
表3 不同环境规划路径数据对比Table 3 Data comparison of planning paths in different environments
由表3中DWA和MCPSO-DWA规划路径长度和用时可知煤矿移动机器人在不同场景中的行驶速度,见表4。从表4可知,在简单环境1中,煤矿移动机器人采用DWA规划路径时行驶速度比MCPSO-DWA快0.12 m/s,但在复杂度增加的后3种环境中,煤矿移动机器人利用MCPSO-DWA规划路径时行驶速度分别比DWA快0.05,0.08,0.19 m/s。这表明MCPSO-DWA在复杂环境中能规划出更合理的路径,同时可以提升煤矿移动机器人的导航效率。
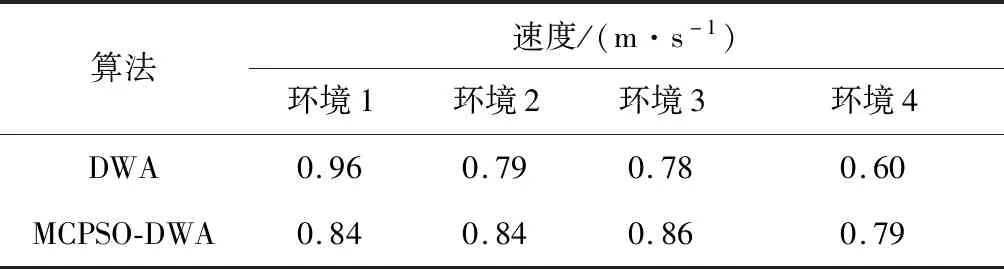
表4 不同环境行驶速度对比Table 4 Comparison of driving speed in different environments
多种路径规划算法在含有U型障碍物的环境中难以逃离U型开口,陷入局部极值。鉴于自适应动态窗口算法(Adaptive-DWA,A-DWA)在复杂环境中规划路径合理性和适应性强的特点,本文在相同含有U型障碍物环境中利用MCPSO-DWA,A-DWA和 DWA进行路径规划,并对比其合理性,用以验证MCPSO-DWA在特殊U型障碍物场景中的适应性。在含有U型障碍物环境中3种算法规划的最优路径对比如图8所示。从图8可看出,DWA和A-DWA在运行过程中面对U型障碍物时未能绕行,在U型障碍物内发生碰撞, MCPSO-DWA可以成功绕过U型开口,到达终点。这说明MCPSO-DWA在不同复杂度环境中都可以进行合理的路径规划,不仅可缩短规划路径的长度,还可明显减少规划路径总步数和时间。
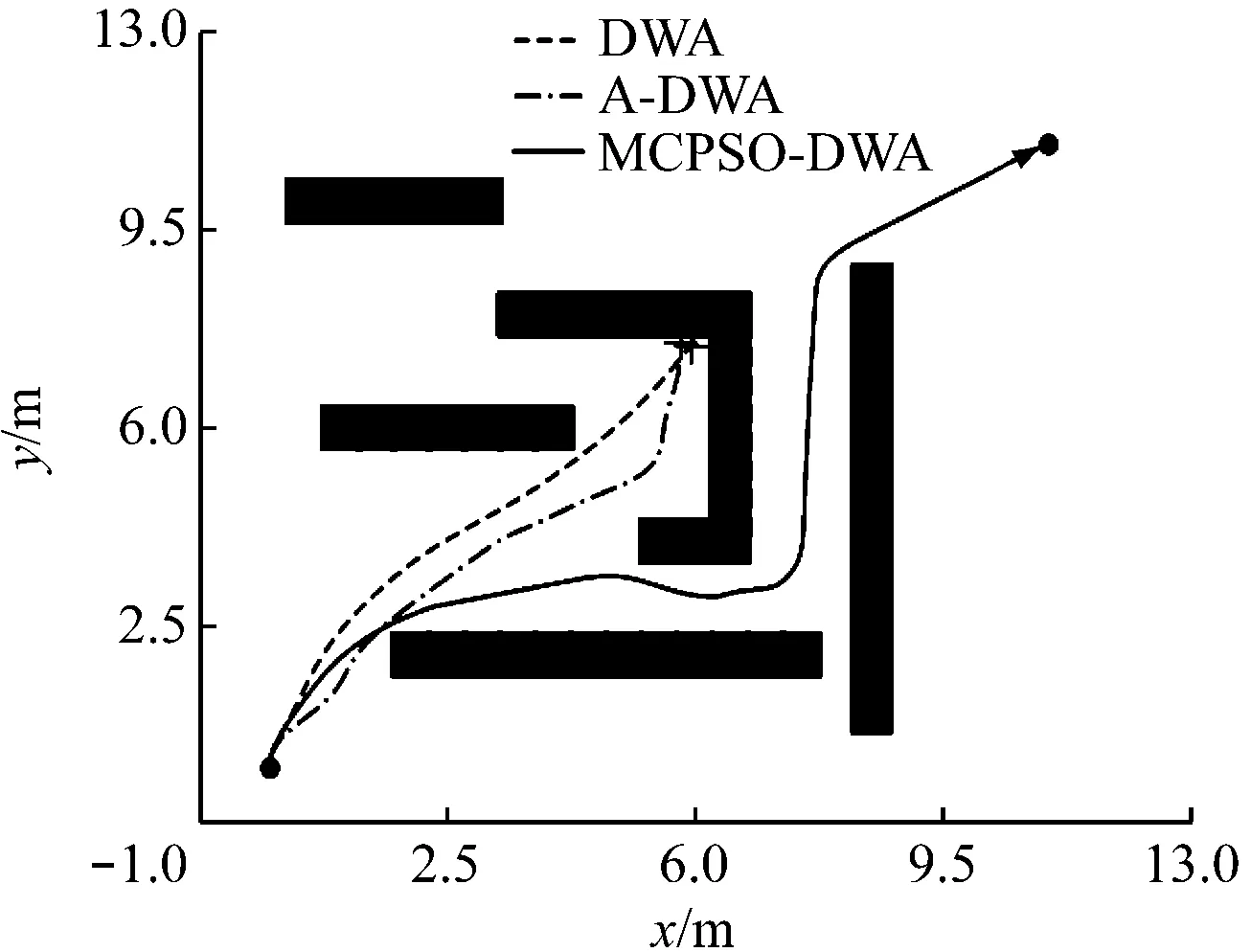
图8 U型障碍物环境中3种算法规划的最优路径对比Fig.8 Comparison of optimal planning paths of three algorithms in U-shaped obstacle environment
4 结语
针对煤矿移动机器人采用传统DWA在复杂环境中规划路径不合理和规划速度慢的问题,提出了基于膜计算和粒子群的煤矿移动机器人动态窗口算法(MCPSO-DWA),该算法通过基于膜计算的粒子群算法对煤矿移动机器人的速度限制区域进行优化,提高了速度采样的随机性和规划路径的合理性,煤矿移动机器人可根据连续时间段间隔内输出的最优速度进行路径规划。实验结果表明,在复杂环境规划路径时,与传统DWA相比,MCPSO-DWA在降低规划步数和每步评价次数的同时,可缩短7%~10%规划路径长度和9%~32%的规划时间,并可适应含U型障碍物的特殊环境。

