基于LM算法的近似核FFT频率拟合算法
周小宁,王立权,朱伟华,闫宏雁,张 宇
(上海机电工程研究所,上海 201109)
0 引 言
单比特测频技术是射频回波模拟器中的一项关键技术,测频结果用于多普勒频率的合成,测频精度会直接影响目标运动速度模拟的准确度,因此提高测频精度对模拟器的性能提升具有重要意义[1-2]。单比特测频技术采用高速模数转换(ADC)(1~4 bit)采样和近似核快速傅里叶变换(FFT)算法引起了系统的非线性[3-4],导致Rife、Quinn等常规频率拟合算法测频精度有限。为此,许多学者做了进一步研究。肖正阳提出的高斯拟合估计法在带宽为2 GHz下测频精度达到1 MHz左右[5]。祝俊、唐斌等人提出了一种基于傅里叶系数内插的频率估计算法,避免了常规算法的复数运算[5-6]。但上述2种算法在频率估计精度方面仍然具有一定的提升空间。
本文在Rife算法的基础上提出了一种基于LM(Levenberg-Marquardt)算法的近似核FFT频率拟合算法,通过特征分类和LM算法[7-9]求解非线性回归问题,实现频率估计。仿真表明,本算法的均方根误差(RMSE)比Rife算法、Quinn算法以及高斯拟合等算法更接近克拉美罗界(CRLB)[6,10],测频精度更高。
1 近似核FFT
在单比特测频中,ADC的量化位数和近似核阶数共同决定了系统的动态范围,由此可以确定两者之间的约束关系[11]:
(1)
ADC位数和近似核阶数并不是越大越好,当ADC位数大于2以及近似核阶数高于8时,系统的动态性能提升有限。因此,这里选择2 bit ADC和8阶近似核作为研究条件。本文利用一种基于半圆的优化近似核代替基于正方形的常规近似核,降低量化噪声,有利于系统的动态性能。近似核结构如图1所示。
2 算法原理
2.1 算法模型构建
Rife算法通过建立最大谱线和次大谱线幅度比R与频率偏差δ之间的理论关系实现频率估计:
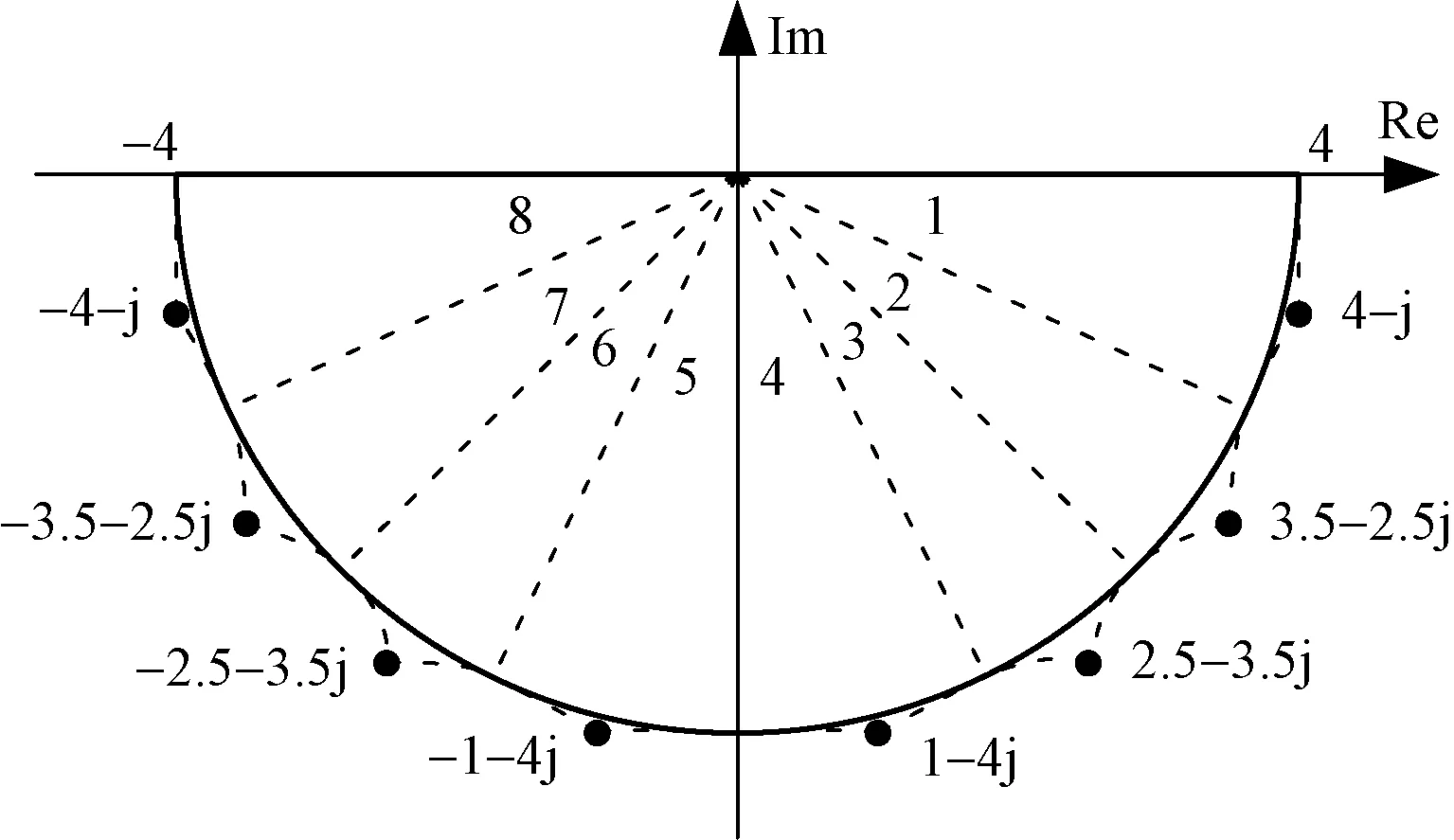
图1 基于半圆的8阶优化近似核
(2)
由于该理论关系建立在常规FFT的基础上,并未考虑近似核算法的影响,在单比特测频系统中应用Rife算法会出现较大偏差,如图2所示。
从图2中可以看出,对于常规FFT,应用Rife算法后频率估计值与理论值基本重合,拟合精度高;而在单比特测频系统中,由于近似核算法的非线性影响,频率偏差理论值呈非对称状态,拟合精度不高。
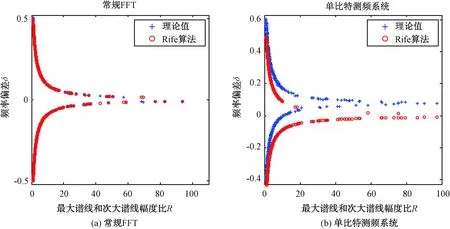
图2 Rife算法频率估计对比图
由此,在Rife算法理论模型的基础上,构建算法模型:
(3)
式中:δ为频率偏差值;R为最大谱线和次大谱线幅度比;xi为待求解的参数。
根据算法模型,首先选取合适的特征及特征值实现频率偏差的分类,在此基础上,通过非线性最小二乘法实现曲线的拟合。
2.2 频率偏差分类
从图2观察可知,R与δ存在一对二的映射关系,在频率拟合时,根据R值无法确定δ的大小。为了简化分析,将图中较大的曲线标为类别1,较小的标为类别2。这样,在测定R值的情况下,需要选择合适的特征以及特征值对频率偏差δ所属类别进行准确区分。
由Rife算法和Quinn算法可知,信号频谱中最大谱线和次大谱线的幅度以及相位与δ值有直接关系。用Aa和Ab分别表示最大谱线及右邻谱线的幅度,φa和φb表示最大谱线及右邻谱线的相位。选择Aa-Ab、φa-φb及φa/φb3种特征进行仿真分析,结果如图3所示。
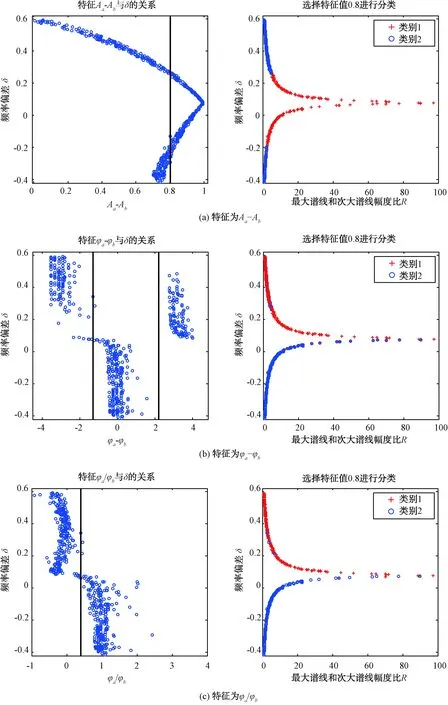
图3 不同特征下频率偏差分类效果图
从仿真结果来看,图3(a)中两类数据点无法有效区分;图3(b)、3(c)中除了个别点以外都能够被区分开来。由此可见,特征Aa-Ab不能对频率偏差实现分类,特征φa-φb和φa/φb均能够满足分类要求,而前者需要设置2个特征值,后者仅需要一个。简单起见,选择特征φa/φb对频率偏差实现分类。
考虑到噪声对分类结果的影响,设置不同的噪声水平对分类性能展开仿真,结果如表1所示。
从表1可以看出,随着噪声水平的提升,分类正确概率有所降低,但依然在98%以上;当信噪比大于15 dB后,分类正确概率达到99%以上,且在不同信噪比下,特征值均稳定在0.41左右,故不需要随着噪声的高低而自适应变化。
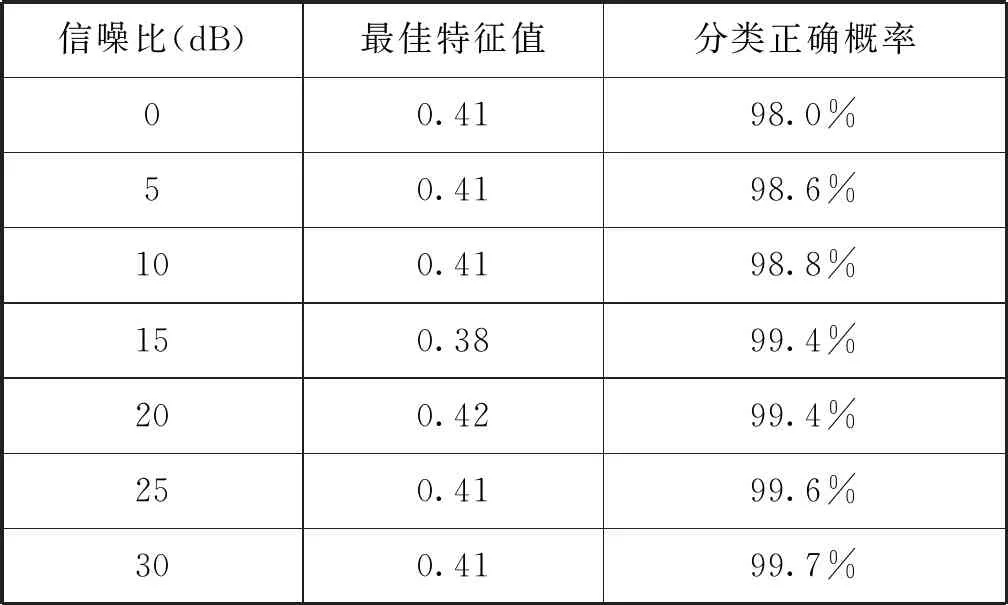
表1 不同信噪比下的特征值和分类正确概
2.3 模型参数求解
由式(3)知,算法模型为非线性方程,只能通过非线性最小二乘法求解未知参数。非线性最小二乘法的求解算法主要有高斯-牛顿法、LM算法和最速下降法,其中LM算法通过阻尼因子自适应调整达到收敛特性,兼顾了高斯-牛顿法和最速下降法两者的优点,具有前者的局部收敛性和后者的全局特性[9],所以,这里采用LM算法进行求解。
采用LM算法求解时,需要由式(3)构建目标函数(代价函数):
(4)
式中:x为待求解的参数向量;Ri和δi分别为输入和输出测量值;m为样本点数。
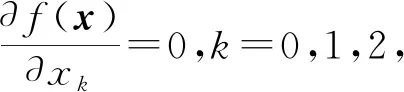
(5)
对于三元非线性方程组,构建雅可比矩阵,记为:
(6)
为了求解式(5)所示的非线性方程组,将其进行泰勒级数展开,通过参数向量x逐次迭代实现求解。设参数向量x的初值为x(0),第k次迭代和第k+1次迭代后的值分别为x(k)和x(k+1),则有算式:
F(x)≈F′(x(k))+J(x(k))(x(k+1)-x(k))
(7)
令Δx(k)=x(k+1)-x(k),则有:
J(x(k))Δx(k)=-F(x(k))
(8)
式(8)为多元线性方程,方程是否存在解的情况取决于雅克比矩阵J(x(k))的正定性,如果矩阵J(x(k))非正定,算法将出现发散情况而无法执行。为了克服上述缺陷,引入阻尼因子μk,式(8)变为:
[J(x(k))+μkI]Δx(k)=-F(x(k))
(9)
上式展开为:
(10)
进而得:
Δx(k)=-[J(x(k))+μkI]-1F(x(k))
(11)
由此可以得到经过第k+1次迭代后的参数向量:
x(k+1)=x(k)-[J(x(k))+μkI]-1F(x(k))
(12)
设定收敛精度ε0,若参数向量x满足精度要求,则有x*=x(k+1),并结束迭代过程。经过求解,得到频率偏差类别1和类别2的拟合曲线方程:
(13)
(14)
综上,本文提出的基于非线性二乘法的拟合算法可以概括为4个步骤:
步骤1:搜索单比特FFT频谱,记录最大谱线的位置mN、最大谱线和次大谱线的幅度比R以及最大谱线和右邻谱线的相位比P;
步骤2:根据P值大小确定频率偏差的所属类别;
步骤3:如果频率偏差属于类别1,则将R值代入式(13),否则代入式(14),求得频率偏差δ。
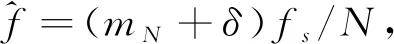
3 仿真验证
为了验证算法拟合性能,采用2 bit ADC,采样频率为25 GHz,对采样信号做4 096点近似核FFT,在2~12 GHz的频率范围内随机选取1 000个频点,统计不同信噪比下频率偏差的拟合程度,仿真结果如图4所示。
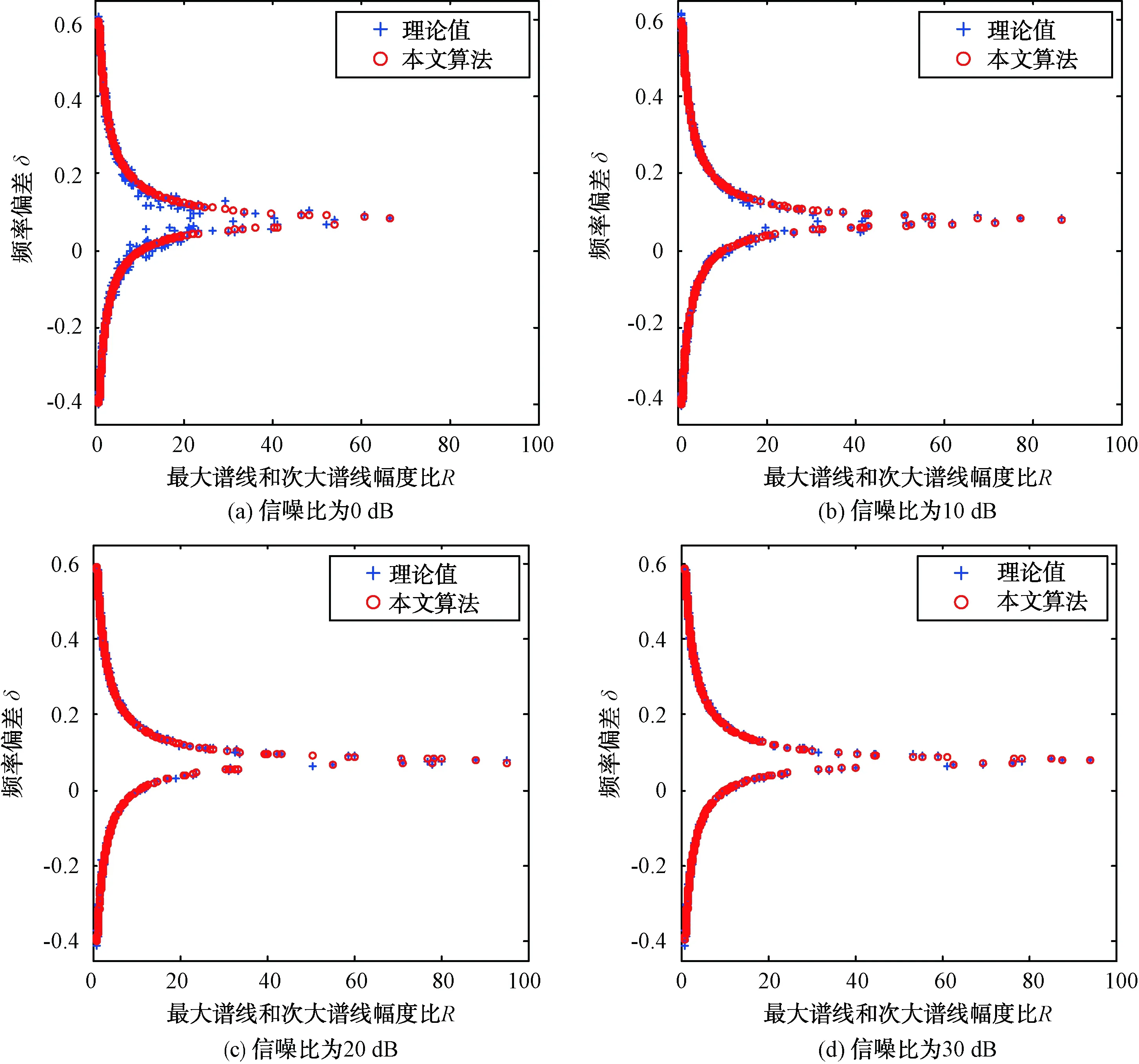
图4 不同信噪比下本文算法拟合效果
由图4可知,随着噪声水平的上升,数据点的分布越杂乱,拟合难度越大,但本文算法仍然有很好的拟合效果。为了直观比较各拟合算法的频率估计性能,对本文算法、Rife算法、Quinn算法以及高斯拟合等算法展开对比仿真,统计不同信噪比下的RMSE和平均绝对误差(MAE),结果如图5所示。
图5中,从RMSE对比结果来看,本文算法比其他拟合算法更接近于CRLB,频率偏差波动更小;从MAE对比结果来看,本文算法相对于其他算法,频率估计精度达到0.1 MHz,测频精度更高。因此,仿真结果验证了本文算法的有效性和优越性。
4 结束语
本文针对常规拟合算法在单比特测频中存在测频精度有限的问题,在Rife算法模型基础上,提出了一种基于非线性最小二乘法的频率拟合算法,利用频率偏差分类和LM算法模型参数求解实现了频率的拟合估计。仿真结果表明,本算法测频精度达到0.1 MHz,与Rife算法、Quinn算法以及高斯拟合等算法相比,在频率估计均方根误差和频率估计精度方面具有一定的优越性。
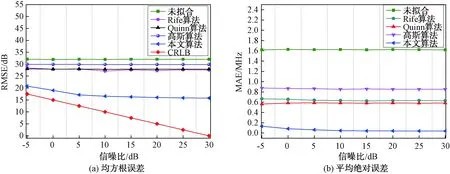
图5 不同算法频率估计性能对比图

