港城联动模式下的内陆港选址
吴小凤 杨璐 赵旭


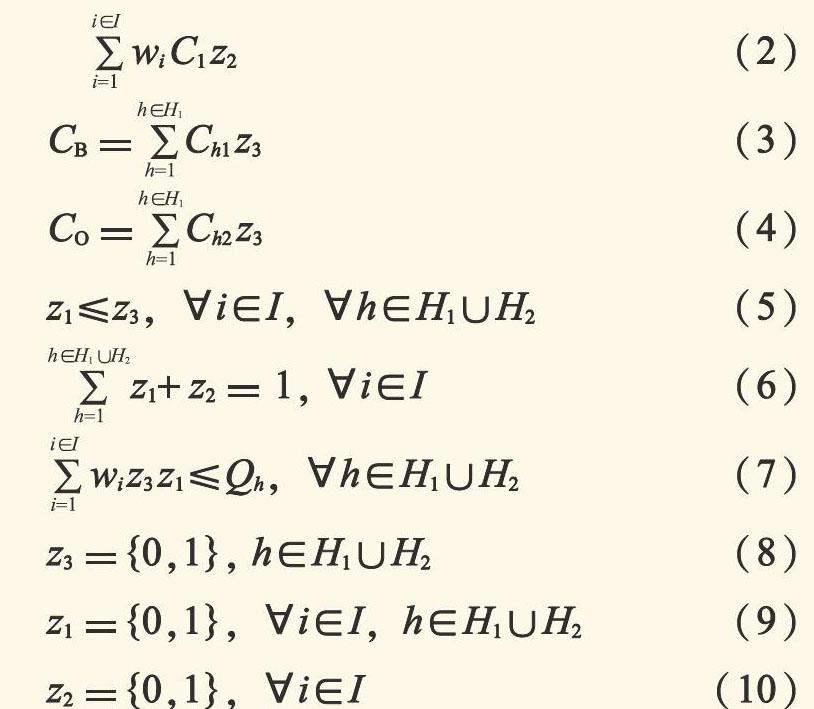
【摘 要】 为有效解决港城矛盾,协调港口与城市发展,以深圳港为例,在模型构建中加入成本折扣系数,并同时考虑内陆港容量限制,以系统总成本最小为目标函数,构建内陆港选址模型,并设计改进遗传算法进行求解。结果表明,全面统筹港口与城市发展,从系统最优角度出发进行内陆港选址研究,能有效优化内陆运输结构,降低运输成本,缓解港城矛盾,实现港城协同可持续发展。
【关键词】 港城联动;内陆港;遗传算法;选址
0 引 言
目前国内港口集疏运以公路运输为主,铁路运输占比较低,导致疏港交通与城市交通互扰,港城矛盾日益凸显。港口为缓解货物吞吐压力、拓展腹地,争先进行内陆港建设;城市为扩大对外开放,亟需低成本、高效率的通关港口,为此也积极投入到内陆港建设中。港口与城市基于各自发展需求进行内陆港建设,导致内陆港布局缺乏系统性和合理性,存在业务辐射范围重叠、效率低下等问题,进一步加剧港城矛盾。内陆港作为连接港口与腹地的重要纽带,其建设发展能否有效完善内陆运输网络,实现公路运输方式向铁路运输的转移,是能否有效解决港城矛盾的重要途径。因此,全面统筹港口与腹地城市协同发展,从系统角度进行内陆港选址研究具有重要意义。
本文从港城协同发展的角度,考虑内陆港形成的规模经济及内陆港容量限制,以系统总成本,包括建设成本、运营成本、运输成本最小为目标函数,进行内陆港选址及货主路径分配研究。
1 问题描述与建模
1.1 问题描述
本文所研究的内陆运输网络由沿海港口、内陆港、货主点构成,其网络拓扑见图1。内陆港运营期间,各货主点进行运输模式选择,选择中转模式即货物经过内陆港转运至港口,选择直达模式即通过公路直达运输至沿海港口。本文基于系统总成本最小化的原则,对备选内陆港的建设及货主点的路径分配进行研究。
1.2 模型假设和参数说明
1.2.1 模型假设
(1)每个货主点选择通过一个内陆港转运至沿海港口或者直达沿海港口。
(2)货主点至内陆港采用公路运输,内陆港至沿海港口采用铁路运输,货主点直达沿海港口采用公路运输。
(3)需求点和备选城市已知。
(4)不考虑运输通道能力限制。
(5)运输的集装箱均为20英尺(约6 m)重箱,每箱装载货物30 t。
(6)内陆港所在城市的运输需求只通过当地内陆港转运。
1.2.2 参数说明
H1为备选内陆港集合,H2为现有内陆港集合;I为需求节点集合, i为需求节点编号,i∈I; O为沿海港口; d1为货主点与内陆港之间的距离; d2为内陆港与沿海港口之间的距离;d0为货主点与沿海港口之间的距离;C1为货物的公路单位运输成本,C2为货物的铁路单位运输成本; a为货物从内陆港运输到港口的折扣系数,0 1.2.3 建立模型 以包括运输成本、中转成本、内陆港的运营成本、新建成本在内的总成本为目标,决策备选新建内陆港和货主点的路径分配。 min f= CT + CB + CO(1) CT= (wi C1 d1 + wi C3 + a wi C2 d2) z1 z3 + wi C1 z2 (2) CB=Ch1 z3(3) CO=Ch2 z3(4) z1≤z3, HOi∈I, HOh∈H1∪H2(5) z1+ z2=1, HOi∈I(6) wi z3 z1≤Qh, HOh∈H1∪H2(7) z3={0,1}, h∈H1∪H2(8) z1={0,1}, HOi∈I, h∈H1∪H2 (9) z2={0,1}, HOi∈I(10) 模型中:式(1)为目标函数,表示系统总成本最小;式(2)为运输成本;式(3)为内陆港建设成本;式(4)为内陆港运营成本;式(5)为货主点只能在内陆港开放运营时才能选择经过此内陆港进行货物运输;式(6)为每个货主点只能选择一条运输路线;式(7)为内陆港的最大容量限制;式(8)、式(9)、式(10)为0或1变量约束。 1.3 求解算法 本文建立的内陆港选址模型是一个非确定性多项式难题(NP问题),求解NP问题的思路是缩小解的搜索范围,并求得较好的近似最优解。本文将采用适于解决全局最优化问题的遗传算法进行求解,并设计接受劣解机制以避免遗传算法陷入局部最优。 2 实例分析 本文以深圳港经济腹地范围内广东省、广西省、湖南省中选取29个城市作为主要货源城市或潜在货源城市,其中韶关、株洲、长沙为现有内陆港,以惠州、东莞、中山、佛山、肇庆、江门、汕头、揭阳、河源、清远、云浮、南宁共计12个城市作为内陆港备选点为研究对象,进行内陆港选址问题研究。 2.1 数据收集 利用出口额推算得出城市运输需求量 Q=n V k1 k2(11) 式中: Q是运输需求量,TEU; V 为出口额,万美元;k1为出口适箱货金额比重,%; k2为出口适箱货生成系数; n为不平衡系数,用于描述运输需求在未来一段时间内的增长趋势。 结合备选城市的区位和辐射能力,设置内陆港最大处理能力,见表1。 a取值1.2,k1取0.8,k2取0.35,n 取值0.8。根据铁路运价的规定及《国际集装箱汽车运输费收规则》,铁路运价和公路运价分别为1.5元/(TEU穔m)和6元/(TEU穔m)。遗传算法种群规模为100,迭代次数为300,交叉概率为0.6,变异概率为0.1,接受劣解概率为0.5。 2.2 模型求解及分析 根据搜集到的数据,利用Matlab软件进行求解,得到内陆港选址及货主点运输路径分配结果(见表2)。结果显示,在惠州市、东莞市、佛山市、揭阳市、南宁市建设内陆港使系统总成本最低,为71.8亿元。 由表2可以看出,有222.91万TEU的出口货物采用公路运输从货源地直接运送至港口,约占货物运输总需求的22%,全部来源于距离港口200 km以内的地区,表明距离港口较近的货主点通过直达运输模式更具经济性。东莞、佛山可作为深圳港的近距离内陆港选址,韶关、揭阳可作为中距离内陆港选址,长沙、株洲、南宁可作为远距离内陆港选址。统筹港口与城市发展,从系统角度进行内陆港建设,能有效实现公路运输方式向铁路运输方式的转移,提高铁路运输占比,缓解港城矛盾。 3 结 语 本文统筹港口與城市协同发展,从系统角度进行内陆港选址研究,考虑内陆港产生的规模经济及内陆港容量限制,以系统总成本最小为目标函数构建内陆港选址模型,并设计改进的遗传算法进行求解。求解得到,在东莞、佛山、揭阳、南宁等城市新建内陆港能实现系统总成本最低,近距离货主点选择直达运输模式更具经济性。港城联动在有利于实现内陆港合理布局、改善内陆运输结构、有效缓解港城矛盾的同时,实现港口与城市稳定可持续发展。

