齿带式油菜捡拾器仿形减振装置设计与试验
江 涛 关卓怀 梁苏宁 李海同 吴崇友 胡志超
(农业农村部南京农业机械化研究所, 南京 210014)
0 引言
油菜分段收获能够延长收获期,充分利用油菜后熟作用提高成熟度一致性,降低收获损失和籽粒叶绿素含量,提高菜籽油品质,因此近年来受到广泛关注[1-2]。捡拾器作为油菜分段收获捡拾脱粒作业环节的主要工作部件,其作业性能对捡拾机整体作业质量至关重要。占总面积90%的冬油菜区田间多水沟、地面起伏不平,在作业时捡拾器对地面高低变化的实时跟踪仿形对于提高捡拾器以及捡拾机的作业性能极其重要。
目前,国内学者对于农业机械仿形机构的研究多集中于精量播种[3-4]、花生收获[5]、残膜回收[6-8]、棉花打顶[9-10]以及其他农业机械装备[11-14],鲜见关于油菜捡拾器仿形机构的研究报道。在田间作业时,路面起伏变化会导致捡拾器弹跳,造成漏捡,驾驶员通过降低作业速度来尽量减小漏检率和损失率,但是即使频繁地调节捡拾台高度以适应地面变化,也不能达到实时仿形的目的,同时还易造成捡拾齿触地铲土,增大籽粒含杂率,甚至导致弹齿损伤。因此捡拾器的地面仿形能力是捡拾器作业质量和作业效率的有效保证。
目前,国外在牧草、秸秆捡拾机械中应用较多的偏心伸缩拨指式及弹齿滚筒式捡拾器多采用整体仿形[15-17],即捡拾器与割台蜗壳采用硬连接,整体通过输送槽下方的油缸进行升降。由于受到结构及尺寸的限制,适用于油菜的齿带式捡拾器多采用铰接式连接,即捡拾器与割台蜗壳采用铰链连接,仿形地轮与割台蜗壳形成捡拾机构的前后支撑,使捡拾器能够绕铰接点转动,以调整捡拾姿态[18]。本文针对铰接式齿带油菜捡拾器,设计一种能够适应复杂地面作业条件的仿形减振装置,通过理论分析确定关键结构与参数,运用中心响应面试验优化方法获得最佳参数组合,并进行田间对比试验,以期为油菜高效仿形捡拾作业提供技术参考。
1 结构与工作原理
捡拾收获机工作时,捡拾器的齿带在主动辊以及从动辊的驱动下逆前进方向回转,待捡拾的物料在捡拾器前进推动以及弹齿的共同作用下被输送至割台输送器,并经由输送槽进入到脱粒滚筒以及清选室,完成后续作业。
铰接式齿带捡拾器(简称捡拾器)主要结构如图1所示,主要包括仿形轮、捡拾齿带、机架、仿形减振装置、锁止杆以及蜗壳等部件。

图1 捡拾器结构图Fig.1 Main structure of pickup header1.待捡拾油菜 2.仿形轮 3.捡拾齿带 4.机架 5.仿形弹簧和阻尼器 6.蜗壳及输送器
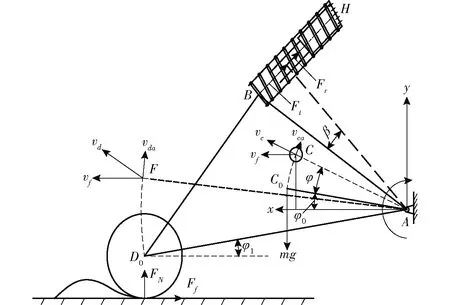
图2 捡拾器动力学分析示意图Fig.2 Schematic of dynamic analysis on pickup
如图2所示,捡拾器正常作业时,割台蜗壳位置保持固定,捡拾器与割台蜗壳铰接于点A处,与水平面的初始相位角为φ1。捡拾器重心位于C0处,与水平面的夹角为φ0。仿形轮与地面接触,轮心位于D0处,当路面起伏时,仿形轮随地面轮廓变化接收并传递来自地面的激励,通过机架将竖直方向上的位移响应等效转换为绕铰接点A的转动响应φ,同时捡拾器重心和仿形轮中心分别移动至C点和D点。为了降低地面激励对捡拾器的影响,在捡拾器与蜗壳之间配置仿形弹簧,使捡拾器仿形轮能够紧贴地面,具备地面仿形能力,并在仿形弹簧内部配置阻尼器来缩短仿形过程中的响应时间,保证作业稳定性,具体如图3所示。
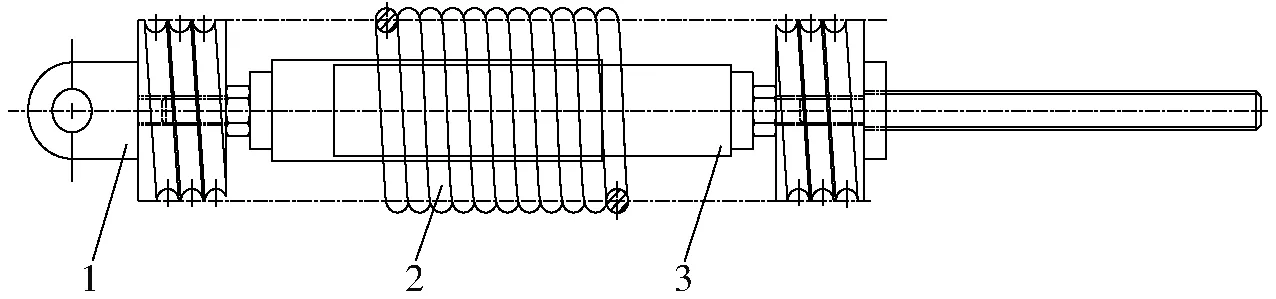
图3 弹簧与阻尼器结构图Fig.3 Structure diagram of spring and damper1.安装座 2.仿形弹簧 3.阻尼器
2 仿形减振装置设计分析
2.1 捡拾器动力学分析
为了研究捡拾器在作业过程中运动特性与装置结构参数之间的关系,应用拉格朗日第二类方程建立捡拾器运动动微分方程[19]。由于捡拾器两侧机架呈对称布置且运动状态保持一致,因此选定一侧进行分析。在图2所示示意图中,系统自由度为1,选取转动响应φ作为广义坐标。由于阻尼器的存在,系统受到的粘滞阻力以及耗散函数为
(1)
式中Fr——阻尼力,N
C——阻尼系数,N·s/m
vr——阻尼器缸体运动速度,m/s
R——系统耗散函数
则系统的拉格朗日方程为
(2)

H——系统动势能,J
T——系统动能,J
V——系统势能,J
捡拾器和仿形地轮的动能分别为
(3)
其中
式中vc——捡拾器质心速度,m/s
vd——仿形轮质心速度,m/s
ω1——捡拾器转动角速度,rad/s
ω2——仿形轮转动角速度,rad/s
T1——捡拾器动能,J
T2——仿形地轮动能,J
vf——机具前进速度,mm/s
Lac——质心到铰接点距离,m
Lad——仿形轮心到铰接点距离,m
J1——捡拾器转动惯量,kg·m2
J2——仿形地轮转动惯量,kg·m2
r2——仿形地轮半径,mm
m1——捡拾器质量,kg
m2——仿形地轮质量,kg
以捡拾器在正常地面作业为零势能面,则
(4)
式中g——重力加速度,m/s2
V1——捡拾器势能,J
V2——仿形弹簧势能,J
δs——仿形弹簧长度变化量,mm
k——仿形弹簧刚度,N/mm
Lab——仿形弹簧底座到铰接点距离,mm
β——仿形弹簧安装倾角,(°)
根据式(2)可得
(5)
将式(5)和式(1)代入式(2)中得到系统运动微分方程为
(6)
由式(6)可以看出,捡拾器在仿形过程中的运动状态特性变化与广义坐标φ、系统响应时间、仿形弹簧刚度k、质心位置、仿形弹簧安装位置以及阻尼器阻尼系数C均有关系。当捡拾器结构确定后,质心位置和仿形弹簧安装位置以及各初始相位角相对确定,则仿形弹簧刚度k、阻尼系数C成为影响系统运动状态的因素。
2.2 仿形装置静力学分析
如图2所示,根据力平衡可得(以逆时针转矩为正)
(7)
式中FN——地面对仿形轮的支反力,N
Ft——仿形弹簧拉力,N
Ff——地面对仿形轮摩擦力,N
f——地面与仿形轮滚动摩擦因数(轮胎与干燥土路一般为0.025~0.035)
L0——仿形弹簧原长,mm
L1——零势能面时仿形弹簧长度,mm
F——地面对仿形轮的作用合力,N
联立求解得
(8)
为了使仿形轮保持与地面贴合稳定接受激励,地面对仿形轮需要保持一定的作用力,即F>0,由式(7)可得
(9)
以仿形轮陷入路面低洼处,仿形轮不受地面作用力作为仿形弹簧的的最大受力位置,设此时绕铰接点O的转角为φ2,有
-FN1Ladcos(φ1+φ2)-Ft1Labcos(β+φ2)+
Ff(Ladsin(φ1+φ2)+r2)+m1gLaccos(φ0-φ2)=0
(10)
式中FN1——低位时地面对仿形轮的支反力
Ft1——低位时仿形弹簧拉力
为使得捡拾器仿形轮不离开地面,根据式(9)可得
(11)
由式(9)、(11)可知,为了满足仿形要求,仿形弹簧应保持一定的预拉力,预拉力过小会使得捡拾器在仿形过程中不足以克服自重而下陷,造成弹齿铲土,过大则仿形轮始终无法贴合地面,造成漏捡。当捡拾器尺寸以及仿形弹簧安装位置确定后,在满足捡拾器最佳工作角度φ0和仿形弹簧有足够伸缩余量的前提下,尽量选择较小的仿形弹簧刚度。为了使捡拾器工作平稳,捡拾器在仿形时的转角φ越小越好,即捡拾器初始相位角应尽可能取较大值,重心与铰接点A的距离以及仿形轮轴线和铰接点的间距AD不应过小[13]。
2.3 减振系统模型及参数分析
捡拾器作业稳定性是作业质量的可靠保证,仿形弹簧能够使得捡拾器仿形轮在作业过程中有效贴合地面,但是在地面条件较差时,仿形弹簧受到外部激励后会处于持续振荡状态,影响仿形质量,因此在系统中加入阻尼器,有助于系统在受到瞬时激励后能够很快恢复到稳定状态,以利于稳定工作。
在仿形过程中,弹簧和阻尼器只承受轴向载荷,并且只在轴向方向上伸缩。如图4所示,仿形系统输入量为路面激励F(t),输出量为系统的轴向伸缩位移s(t),有
(12)
式中ξ——阻尼比m——捡拾器总质量
ωn——系统无阻尼固有频率,Hz
ωd——有阻尼自然角频率,rad/s
c——粘性阻力系数

图4 仿形减振系统示意图Fig.4 Sketch of profiling and damping system
若ξ小于0,仿形系统会产生发散,造成不稳定,大于1为过阻尼,系统响应将不存在超调,没有振荡。在本文中主要考虑欠阻尼情形,即ξ介于0到1之间。
建立仿形减振系统的目的是避免捡拾器在高低不平田面上作业时产生弹跳,因此要求捡拾器遇到激励时在垂直方向上具有较小的位移。考虑采用脉冲响应函数法来描述地面对捡拾器的非周期激励强迫振动[20],如图5所示,设捡拾器受到的来自于凸起路面的激励为脉冲函数激励,脉冲力F(t)=P0δ(t),方向垂直于地面向上,代入式(12)可得
(13)
式中P0——脉冲力
δ(t)——脉冲力作用时间
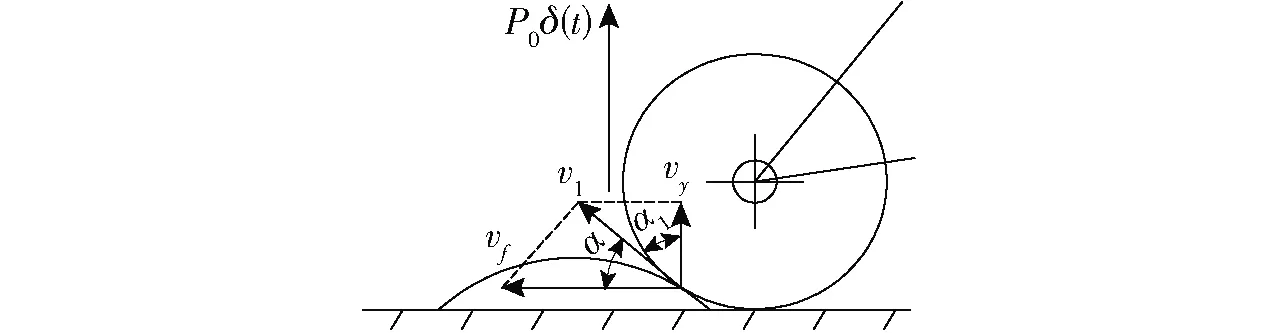
图5 脉冲激励Fig.5 Pulsed excitation
当地面脉冲激励对系统产生瞬时作用后,系统对该脉冲激励的响应值为
(14)
令P0=1,当t=0时作用的单位脉冲为δ(t),系统响应为s(t),t=a时刻,单位脉冲为δ(t-a),系统响应为s(t-a),则对于任意脉冲激励函数,在任意时间点τ,系统对于该脉冲激励的响应为F(τ)Δτs(t-τ)。由于系统在某一时间点的响应应当为在此时间点之前所有时间点τ系统响应的叠加,则在t时刻,系统响应为
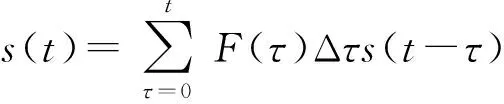
令Δτ→0,有

结合式(14)有
(15)
由于捡拾器在激励作用初始时刻处于正常作业状态,因此系统除了受到F(t)这一过程激励作用外,还存在前进速度对其的影响,如图5所示。
vy=vfcosαcosα1
(16)
式中vy——激励作用后捡拾器具有的竖直方向速度,m/s
α、α1——外部激励决定的速度分量倾角,(°)
则此时系统的综合响应为
(17)
由式(17)可以看出,捡拾器的仿形减振系统对于外加激励的响应是由m、ωd、ξ、ωn等系统内在特性以及系统在激励作用瞬时所具有的初始速度决定。随着ξ和ωn的增加,系统能够以更快的响应速度达到稳定,即在捡拾器结构以及质量确定后,应尽量选择较大的系统刚度。但是由前述分析可知,过大的刚度会影响仿形弹簧伸缩距离并且会产生过大的预拉力,造成上仿形漏捡或下仿形铲土,因此对于仿形弹簧刚度以及阻尼比的选择需要综合考虑。
3 仿形稳定性优化试验
3.1 试验方法
试验采用基于响应面法的Box-Benhnken组合设计[21-22],由前述分析可知,捡拾器的仿形减振系统作业效果受到仿形弹簧刚度k、系统阻尼比ξ以及捡拾器前进速度vf的影响,选取这3个因素作为试验因素,因素编码如表1所示。

表1 试验因素编码Tab.1 Codes of test factors
为了评价仿形减振系统作业效果,选取图2所示铰接点A的峰值角度与标准角度变化的平均误差(以下简称角度均差)Y1以及仿形稳定性变异系数Y2作为评价指标,评价方法如下:
由于捡拾器仿形轮在路面激励作用下竖直方向上的位移可以转换为铰接点A处的转角Δφ,由第2节分析可知,当捡拾器仿形准确度高时,仿形轮应当时刻紧贴地面,因此对于不同的地面高度变化Δh总有对应的Δφ。为了保证路面对仿形轮激励的一致性,人工设置高度分别为50、100、150 mm的障碍物各3组,按高度依次摆放于平整台面上,具体结构如图6所示。

图6 人工设置障碍示意图Fig.6 Schematic of artificial obstacle
机器以匀速依次通过各组障碍,在图2所示A点处安装角度传感器并记录角度变化,通过计算经过障碍时的角度均差Y1以及仿形稳定性变异系数Y2评价仿形稳定性,计算式为
(18)
式中S——各激励下的峰值角度均差标准差
Δφi——第i个激励对应的标准角度变化值
φi——第i个激励测得的峰值角度
进行仿形稳定性试验,如图7所示。

图7 仿形稳定性试验Fig.7 Profiling stability test
3.2 试验结果分析
3.2.1角度均差回归模型与显著性分析
试验方案与结果如表2所示(A、B、C为因素编码值),对角度均差进行方差分析,结果如表3所示。可以看出,模型P值小于0.01,表明回归模型极显著,失拟项P值大于0.05,表明模型误差小,该模型可用于仿形角度均差的预测。

表2 试验设计方案及结果Tab.2 Test design scheme and results
在该回归模型中,A、B、C、AB、A2、B2的P值小于0.01,表明在95%的置信区间内,这些因素对于回归模型的影响极显著。AC、BC、C2的P值小于0.05,表明在95%的置信区间内,这些因素对于回归模型的影响显著。
各试验因素对于回归模型的影响显著性由大到小为B、A、C,拟合回归方程为
Y1=2.4+0.24A+0.34B+0.15C-0.2AB-
0.093AC+0.13BC+0.14A2+1.49B2+0.12C2
(19)
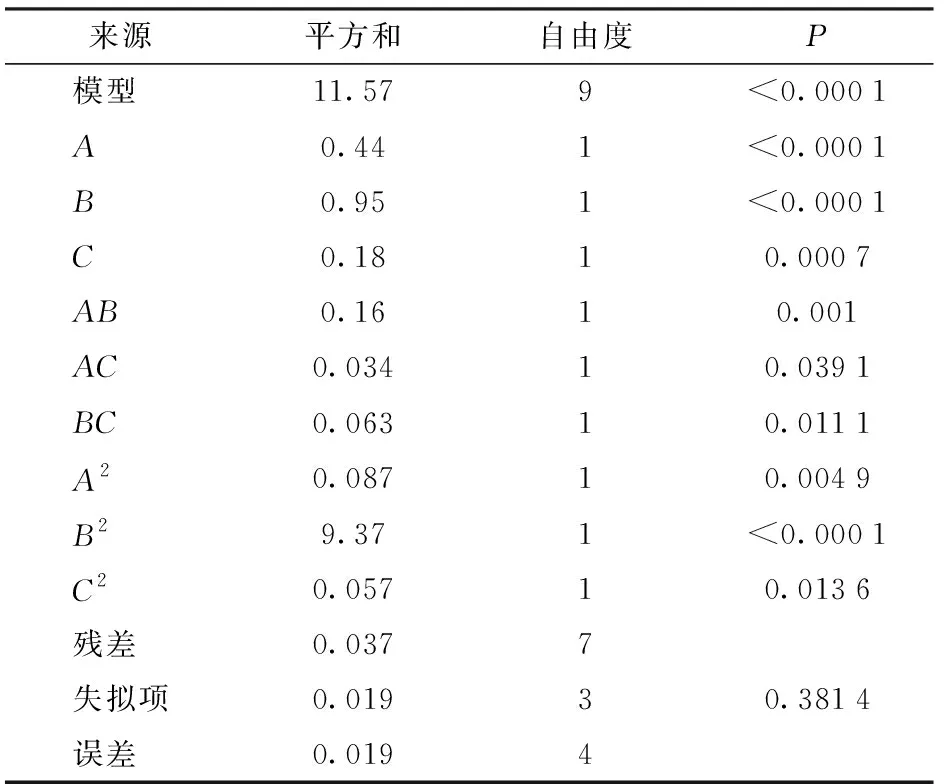
表3 角度均差方差分析Tab.3 Variance analysis of average degree deviation
3.2.2仿形稳定性变异系数回归模型与显著性分析
对仿形稳定性变异系数试验结果进行方差分析,结果如表4所示。由表4可以看出,模型P值小于0.01,表明回归模型极显著,失拟项P值大于0.05,表明模型误差小,该模型可用于仿形稳定性变异系数的预测。
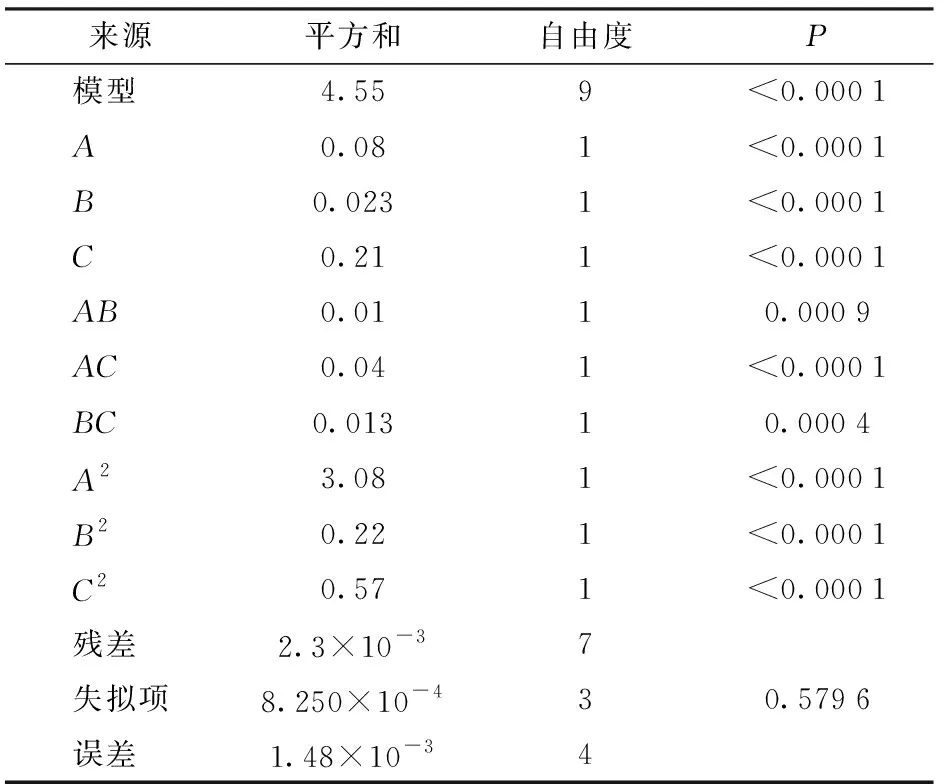
表4 仿形稳定性变异系数方差分析Tab.4 Variance analysis of profiling stability variation coefficient
在该回归模型中,A、B、C、AB、AC、BC、A2、B2、C2的P值小于0.01,表明在95%的置信区间内,这些因素对于回归模型的影响极显著。
各试验因素对于回归模型的影响显著性由大到小为C、A、B,拟合回归方程为
Y2=6.24+0.10A+0.054B+0.16C-0.05AB+
0.1AC+0.058BC+0.86A2+0.23B2+0.37C2
(20)
3.2.3各因素对角度均差的影响分析
由图8可知,在弹簧刚度的各个水平下,随着阻尼比的增加,角度均差呈现先降低后增加的趋势,表明在欠阻尼的情况下,高阻尼比使得捡拾器与割台之间的连接接近于刚性连接,导致捡拾器在需要仿形时难以绕铰接点旋转,造成整体冲击过大,而过低的阻尼比无法提供有效的约束会使得捡拾器在需要仿形时产生过度转动。当阻尼比位于0水平,在较低的弹簧刚度水平下,随着前进速度的升高,角度均差呈现逐渐上升的趋势,表明过高的前进速度会使得捡拾器在经过障碍时具有更大的冲量,造成弹跳;而过大的弹簧刚度产生的拉力也同样会加剧捡拾器越障时的弹跳。当弹簧刚度位于0水平时,在前进速度的各个水平下,角度均差随着阻尼比的升高呈现先降低再升高的趋势。

图8 交互作用对角度均差影响响应曲面Fig.8 Surface diagrams of interactions on average degree deviation
3.2.4各因素对仿形稳定性变异系数的影响分析
由图9可知,在弹簧刚度保持在9.3~10.7 N/mm范围内,随着阻尼比和前进速度的升高,仿形稳定性变异系数呈现先降低再升高的趋势,说明在欠阻尼的情况下,阻尼比升高会降低仿形稳定性,高阻尼比会使得捡拾器与割台之间的连接接近于刚性连接,捡拾器绕铰接点的旋转特性出现变化。过高的前进速度也会造成仿形系统受到外部激励后的综合响应时间增加,增加不稳定性。由图8c可知,在仿形装置系统阻尼比保持在一定水平时,随着前进速度的变化,角度均差呈现先降低后升高的趋势,但是变化较为缓和。同样的,当阻尼比保持在一定水平时,随着机具前进速度的增加,稳定性变异系数同样呈现较为平缓的变化趋势。
3.2.5参数优化
为了达到仿形减振系统的最优性能,以角度均差和仿形稳定性变异系数最小为优化目标,对弹簧
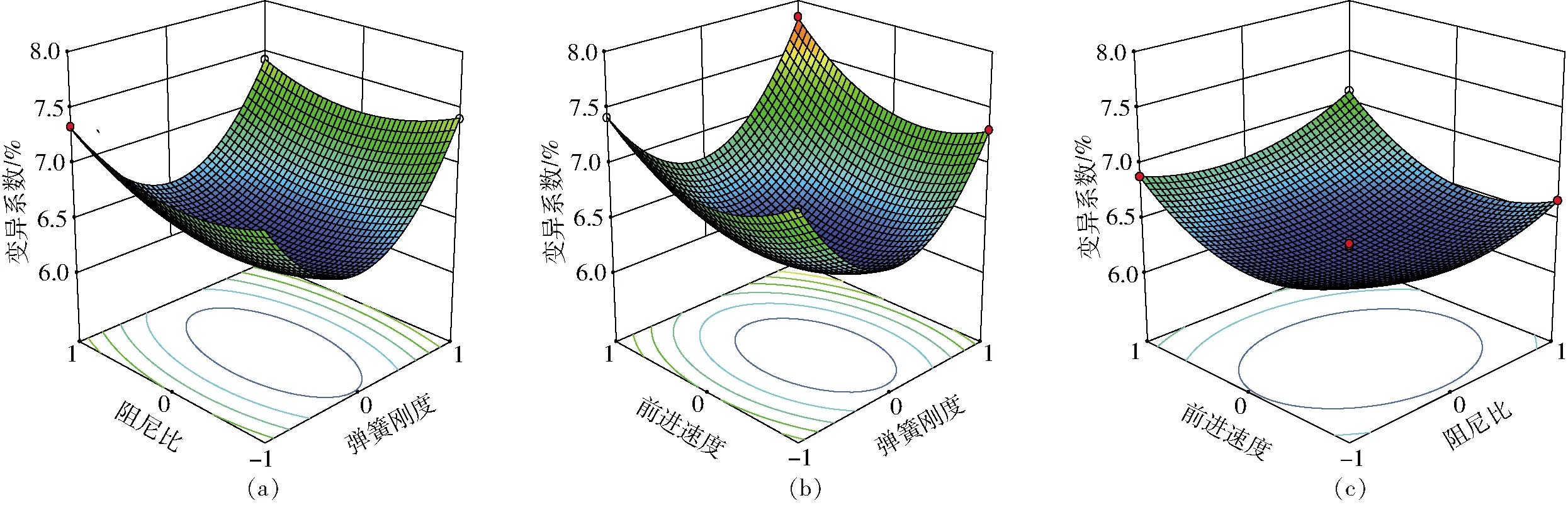
图9 交互作用对仿形稳定性变异系数影响响应曲面Fig.9 Surface diagrams of interactions on profiling stability variation coefficient
刚度、阻尼比和机具前进速度进行优化设计,结合试验约束条件,建立目标及约束函数
(21)
运用数据统计软件对模型进行分析求解,优化后的最佳参数组合为:弹簧刚度9.7 N/mm、阻尼比0.38、前进速度0.95 m/s,对应理论角度均差为2.3°,仿形稳定性变异系数为6.2%。
4 对比试验
4.1 场地对比试验
采用与3.1节相同的方法进行场地分组对比试验,其中A组为不挂接本文设计仿形减振系统的捡拾机,B组为挂接机具并选用接近优化结果的结构参数:刚度10 N/mm,阻尼比0.4,机具前进速度统一为0.95 m/s。试验重复3次,具体试验结果为A组角度均差6.8°,仿形稳定性变异系数9.21%;B组角度均差2.41°,仿形稳定性变异系数6.28%。结果表明,在挂接了仿形减振装置后,捡拾器仿形准确度以及仿形稳定性均有提升。
4.2 田间对比试验
为了明确仿形减振系统对于实际作业质量的影响,于2019年6月2日在盐城市大丰区进行了田间对比试验,试验选取地面状况复杂、平整度差、土壤坚实度高的田块进行。试验油菜品种为宁杂1818,理论产量3 600 kg/hm2,前序作业采用油菜割晒机在油菜70%~80%成熟度时进行割倒、铺放并晾晒4 d(割晒损失忽略不计),留茬高度统一保持20 cm,试验时籽粒含水率16.1%,符合油菜捡拾作业要求。试验现场如图10所示。

图10 田间试验Fig.10 Field test
试验选取含杂率和损失率为指标,为了排除仿形减振系统之外的因素影响,机具的所有其他结构以及作业参数保持一致,为了区分效果,选用弹簧刚度10 N/mm,阻尼比0.4,机具前进速度0.95 m/s。试验分为A、B两组进行,其中A组为不挂接本文设计仿形减振系统的捡拾机,B组为挂接后的机具。在田块内随机选取5个试验区域,每个区域内选取50 m长的测区,测区内随机选取5个采样点进行采样,计算平均损失率。每个测区试验结束后,在粮仓内随机采样5次计算平均含杂率。损失率和含杂率计算公式为
(22)
(23)
式中W1——采样点采样落粒质量,g
W2——粮仓内采样的杂质质量,g
W——一个测区内的油菜籽粒总质量,g
田间对比试验结果如表5所示,A组平均捡拾损失率6.54%,平均含杂率4.45%,B组平均损失率4.53%,平均含杂率3.22%。
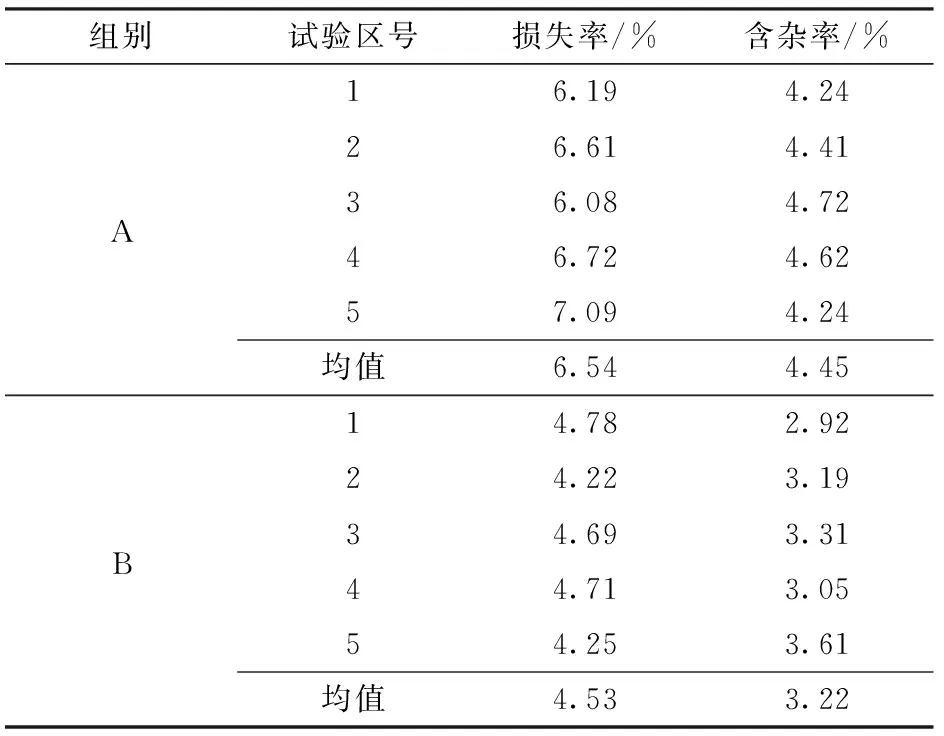
表5 作业质量对比试验结果Tab.5 Comparative test results of operation qualities
由试验结果可以得出,具有仿形减振系统的捡拾机比没有方形减振系统的捡拾机捡拾损失率和含杂率分别降低了30.73%和27.64%,效果显著。通过观察试验过程可以发现,在捡拾器地轮经过有明显凸起的地面时,捡拾器发生弹跳,造成部分油菜漏捡;而在经过某些坚实度较低的起伏路面时,由于没有系统的束缚,捡拾器因自重而造成捡拾弹齿铲土,是造成含杂率高的主要原因。
5 结论
(1)为了提高齿带式捡拾器地面仿形效果,设计了由弹簧和阻尼器共同组成的仿形减振装置,在对仿形减振装置进行动力学、静力学分析的基础上,建立了仿形减振系统模型。
(2)通过对角度均差和仿形稳定性变异系数的响应面试验,确定了对峰值角度均差的影响由大到小依次为阻尼比、弹簧刚度、前进速度,对仿形稳定性变异系数的影响由大到小依次为前进速度、弹簧刚度、阻尼比。通过软件系统寻优确定了仿形稳定性最佳参数组合为:弹簧刚度9.7 N/mm、阻尼比0.38、前进速度0.95 m/s,对应的理论角度均差为2.3°,仿形稳定性变异系数为6.2%。
(3)田间对比试验表明,挂接仿形减振装置的捡拾器平均捡拾损失率4.53%,平均含杂率3.22%,分别比未挂接减振装置的捡拾器降低了30.73%和27.64%,作业效果提升明显。

