粒径对液滴静电聚结微观特性影响的实验研究

孙治谦,刘伯川,李 宁,蒋 燕,周衍涛,王振波

(中国石油大学(华东)新能源学院,山东 青岛266580)

1 前 言

近年来，随着国内众多油田进入开采末期，地层能量较低，为满足开采需要，多采用注水、注剂的方式驱油，使得原油含水量大大增加，原油乳化、老化程度加深[1-2]，这不仅增大了原油集输系统的负荷，还对现有的电脱装置造成不利影响：脱后含盐含水严重超标；装置操作不稳，出现电流过大、垮电场甚至极板击穿现象；切水严重带油，给后续污水处理系统带来严重冲击[3-6]。

脉冲电聚结技术是20世纪80年代由Bailes等[7]提出的一种采用非连续电压的电聚结技术，存在振荡聚结、偶极聚结、强场冲击和水链聚结的叠加效应，与交流、直流和交直流等静电聚结方法相比，具有能耗小、效率高的显著优势，在应对原油含水量增高、乳化程度加深的趋势上，具有很大的应用潜力[8-10]。

自此，国内外学者对脉冲电聚结技术展开了相应研究，但大多集中在电场参数、操作参数层面，对电聚结效果的评价多停留在宏观电聚结性能层面[11-14]，也有从乳状液分散相液滴的聚并、变形、破碎层面入手的相关研究[15-19]，但从液滴粒径角度开展的研究较少。张建等[20]基于脉冲电场下油包水乳状液中水滴的受力情况，建立乳状液水滴振荡固有频率公式，其固有频率受液滴粒径的影响较大。彭烨等[21]运用电流体动力学理论，建立和乳状液分散相液滴粒径相关的电介质物理学模型，来预测脉冲电场作用下油中液滴的振动变形，计算得到的液滴振动伸缩变形量与实验结果相近。Mousavi 等[22]对乳状液中二次液滴形成的影响因素进行研究，结果表明，形成二次液滴的阈值频率取决于脉冲电场的波形、电场强度以及液滴的粒径。为全面考察脉冲电场下液滴粒径对乳状液油包水(W/O)分散相液滴变形、聚并、破碎等特性，本文借助显微观测系统，从微米尺度液滴层面入手，揭示粒径对液滴静电极化变形、聚并、破碎的影响规律。

2 实验装置与方法

图1 实验装置示意图Fig.1 Schematic diagram of theexperimental set-up

实验主体装置如图1所示，由高压高频脉冲电源、电聚结单元、数码生物显微镜及计算机等组成。实验时采用医用注射器向连续相油相中置入水滴，通过变换注射针头的尺寸，可改变所滴入水滴的粒径。然后施加高压高频脉冲电场，通过数字显微成像系统，观察液滴的极化变形、聚并、破碎过程。水滴的粒径、间距以及水滴变形后的长轴、短轴等尺寸信息，均可通过显微图像分析软件测得，进而转化为所需的变形度、聚并速率等信息，并以此来分析水滴粒径对液滴静电极化变形、聚并、破碎的影响规律。其中，实验过程中所选用的导热油、机油、蒸馏水及200 mg.L-1表面活性剂OP-10水溶液在20℃时的物性参数如表1、2所示。

3 实验结果与分析

施加高压高频脉冲电场后，W/O乳状液中的水滴在电场力的作用下会发生极化变形、聚并、破碎等过程，为表征水滴在电场作用下的变形程度，将极化变形前后的水滴简化，如图2所示，并提出变形度D的概念，变形度D越大，表示水滴偏离球体的程度越大，变形程度越明显。图2中dp为水滴变形前粒径，μm；表示范围无穷大均匀电场。变形度如式(1)所示：式中：D为水滴变形度，%；a为极化水滴的长轴长度，μm；b为极化水滴的短轴长度，μm。

表1 油水表面张力Table1 Interfacial tensions between oil and water

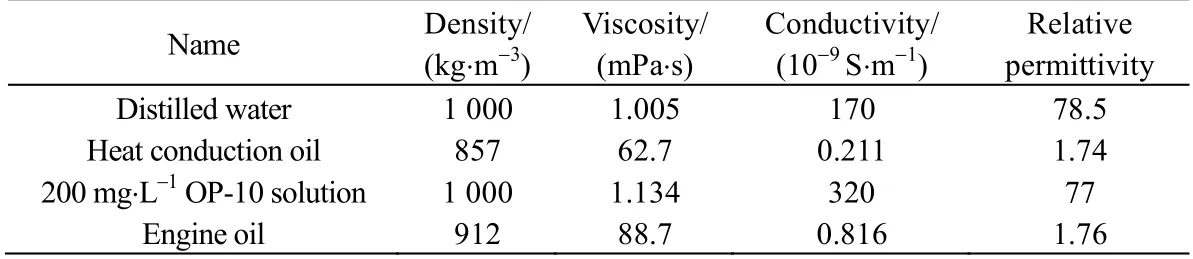
表2 实验油品及水溶液物性参数Table2 Physical parametersof experimental oilsand aqueoussolutions

同时，为方便实验结果的讨论，另提出以下辅助参数：水滴平均变形度，%：即两水滴在高压高频脉冲电场作用下变形度的平均值，如式(2)所示：

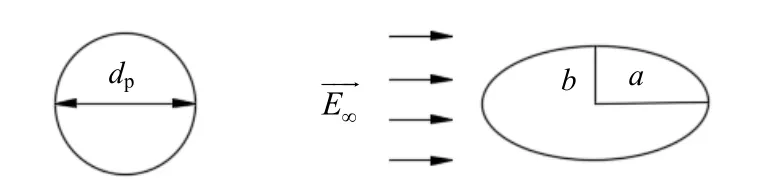
图2 水滴极化变形前、后简化模型Fig.2 Simplified model of water droplet before and after deformation

式中：D1为两水滴中1号水滴变形度，%；a1为1号水滴极化变形后长轴长度，μm；b1为1号水滴极化变形后短轴长度，μm；D2为两水滴中2号水滴变形度，%；a2为2号水滴极化变形后长轴长度，μm；b2为2号水滴极化变形后短轴长度，μm。

水滴相互靠近速率：水滴近端距离在电场作用时间段内的变化率，单位：μm.s-1，取值为正表明两水滴相互靠近；取值为负表明两水滴相互远离。

聚并时刻比：所考察时间t与水滴自初加电场到聚并发生时刻所用时间tk的比值。聚并时刻比为0，表示此刻刚刚施加电场，水滴开始相互靠近；聚并时刻比为1，表示此刻两水滴相互接触，并开始发生聚并。

水滴临界变形度：水滴在极化变形过程中保持椭球形变形的极限值，以符号Dc表示，%。

3.1 水滴粒径对液滴极化变形的影响

在考察水滴粒径对液滴极化变形的影响时，采用导热油为连续相、蒸馏水为分散相。如图3、4所示分别为不同水滴粒径条件下水滴变形度随电场频率、占空比变化的曲线。由图3 可知，在电场强度为4.283 kV.cm-1，占空比为50.1%时，不同粒径水滴的变形度均随着频率的增大而增大，原因是水滴在脉冲电场下的“球体-椭球体-球体”振动频率随着电场频率的增大逐渐增大，并逐渐接近水滴的固有频率，从而产生共振效应，使水滴的振动幅度变大，变形度故而增大。从图4 中可看出，在电场强度为4.283 kV.cm-1，频率为4 kHz时，不同粒径水滴的变形度随占空比的增大先快速增大后缓慢减小，这是由于占空比较小时，单个脉冲周期内电场有效作用时间很短，作用于水滴的电场能较小，水滴变形度和临界变形度有较大的差距，此时随着占空比的增大，水滴变形度随电场能的增加快速增加，当占空比达到60%后，水滴变形度随着占空比的增大略微降低。其原因在于当占空比达到60%时，水滴的变形度已接近其临界变形度，此时占空比进一步增大，由于场强低于水滴临界破碎场强，水滴不发生破碎，而在界面张力作用下发生小幅回弹。

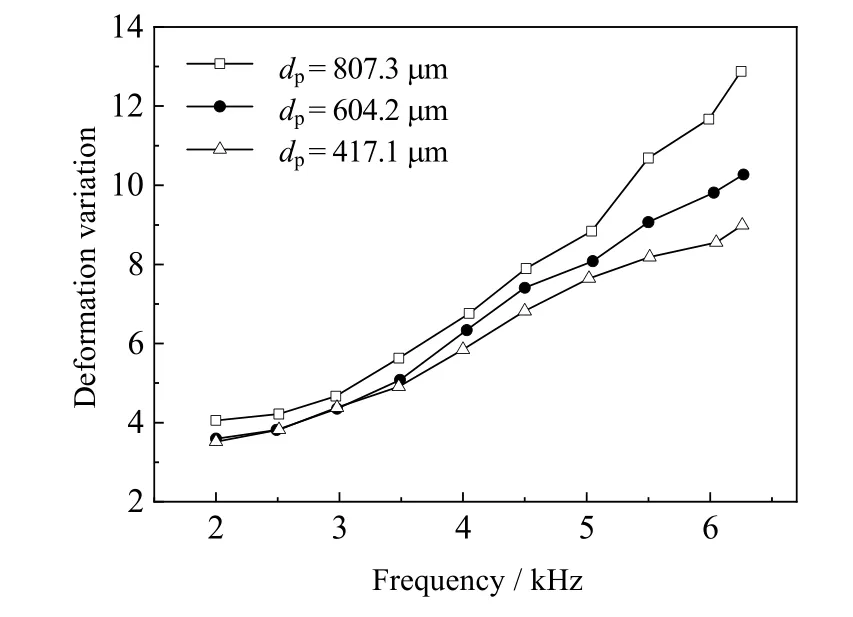
图3 不同粒径下变形度随频率的变化曲线Fig.3 Deformation variation as a function of frequency under different droplet sizes

图4 不同粒径下变形度随占空比的变化曲线Fig.4 Deformation variation as a function of duty ratio under different droplet sizes

此外，从图3、4中还可以看出，实验条件下，水滴的变形度随水滴粒径的增大而增大，且在2～6 kHz、0～60%占空比时，水滴变形度增大的程度随频率、脉宽比的增大而增大。原因在于，根据Laplace公式(式(3))可知，油水界面张力不变时，水滴粒径增大导致水滴内外压差变小，水滴抵御电场力变形的能力变小，变形度随之增大。当频率和占空比较低时，作用于水滴的电场能较小，水滴的振动变形幅度小，因此不同粒径水滴间变形度的差别较小；当频率和占空比升高时，作用于水滴的电场能随之变大，水滴的振动变形幅度变大，不同粒径水滴间变形度的差别变大。当占空比达到60%后，不同粒径水滴均会随占空比的增大出现小幅度的回弹，此时不同粒径水滴间的变形度差别不再继续变大或出现略微减小的现象。

式中：Δp为水滴内外压力差，Pa；r0为小变形条件下水滴半径，m；σ为油水界面张力，N.m-1。

3.2 水滴粒径对液滴聚并的影响

在研究水滴粒径对液滴聚并的影响时，采用导热油为连续相、质量浓度为200 mg.L-1的OP-10蒸馏水溶液为分散相，实验中液滴对粒径相同，两水滴中心线方向和电场方向夹角为零度，电场强度为0.906 5 kV.cm-1，电场频率为3 kHz，占空比为50%。两水滴在脉冲电场下聚并的过程如图5所示。

图5 两水滴在脉冲电场下的聚并过程Fig.5 Coalescence of two water dropletsunder pulsed electric field

如图6所示为不同粒径水滴平均变形度随聚并时刻比变化的曲线。由图6可知，随着水滴粒径的增大，水滴平均变形度总体呈增大的趋势。原因主要有两点：首先，根据Laplace 公式可知，油水界面张力不变时，水滴粒径增大导致水滴内外压差变小，水滴抵御电场力变形的能力变小，单个液滴变形度随之增大；其次，由偶极-诱导-偶极模型(式(4))可知，水滴粒径增大，导致两水滴间的偶极聚结力增大，两水滴异电荷端引力增大，使两水滴相互极化引起的变形也随之增加。

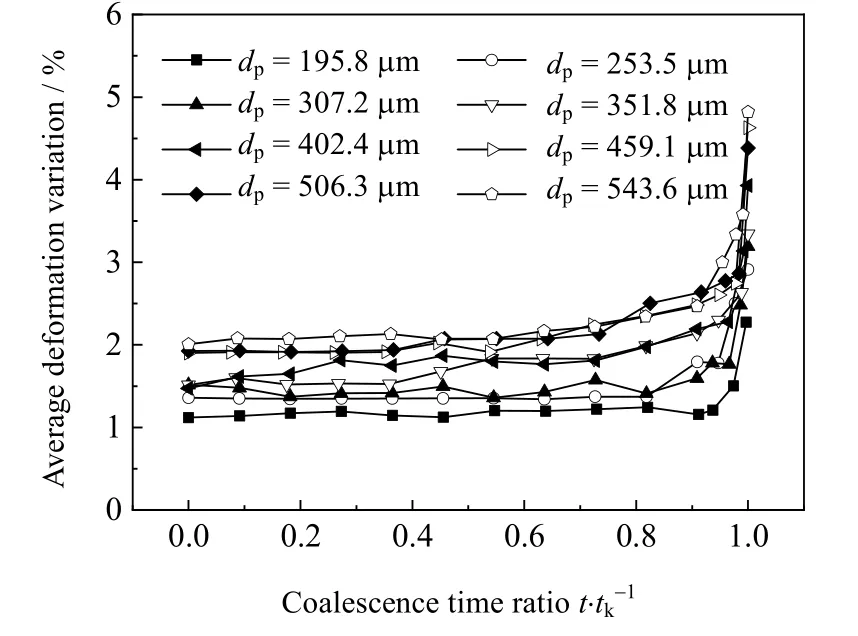
图6 平均变形度随粒径的变化曲线Fig.6 Averagedeformability variation as a function of droplet size

图7 水滴相互靠近速率随粒径的变化曲线Fig.7 Dropletsapproaching velocity as a function of droplet size

如图7所示为不同粒径水滴靠近速率随聚并时刻比变化的曲线。总体来看，水滴相互靠近速率随粒径的增大而增大。这是由于在两水滴中心距不变的情况下，随着水滴粒径的增大，两水滴的极化变形度增大，水滴近端距离减小，另外由于水滴间的偶极聚结力增大，使得相互极化吸引作用力增大，水滴相互靠近速率故而随之增大。

式中：Fdipole为两水滴间偶极聚结力，N；β为克劳修斯-莫索提系数，大小为(εw-εo)/(εw+2εo)；εw为水相介电常数，F.m-1；εo为油相介电常数，F.m-1；E为外加电场强度，kV.cm-1；r1为两水滴中1号水滴未变形时半径，m；r2为两水滴中2号水滴未变形时半径，m；δ为两水滴中心距，m；K为无量纲系数，两水滴中心距趋于无穷时，K趋近于1。

3.3 水滴粒径对液滴破碎的影响

在考察水滴粒径对液滴破碎的影响时，采用机油为连续相、质量浓度为200 mg.L-1的OP-10蒸馏水溶液为分散相，实验中水滴的破碎过程如图8所示。

图8 水滴在脉冲电场下的破碎过程Fig.8 Breaking up processof water droplet under pulsed electric field

如图9、10所示分别为不同电场频率f和不同占空比n下临界场强随水滴粒径变化的曲线。由图可知，水滴破碎的临界场强随着水滴粒径的增大逐渐降低，这是因为水滴粒径增大时，水滴附加压应力变小，水滴抵御电场力变形的能力变小，水滴发生破碎对应的电场力减小，水滴发生破碎临界场强随之降低。另外，从图中还可以看出，相同粒径水滴的临界破碎场强随占空比和电场频率的升高而降低，这和图3、4所描述的规律相一致，当电场频率和占空比增大时，水滴极化频率和振荡频率增加，作用于水滴的电场能增大，水滴变形度接近其临界变形度的速度更快，水滴破碎临界场强随之降低。

图9 不同频率下临界场强随粒径的变化曲线Fig.9 Critical field intensity variation asa function of granularity under different frequencies

图12 不同占空比下临界变形度随粒径的变化曲线Fig.12 Critical deformability variation as a function of granularity under different duty ratios

如图11、12所示分别为不同电场频率和不同占空比下水滴临界变形度随水滴粒径变化的曲线。由图可知，水滴的临界变形度总体上随水滴粒径的增大有所降低。根据图9、10得出的规律可知，当水滴粒径增大时，水滴的临界破碎场强减小，要达到破碎的条件对应的水滴附加压应力变小，粒径较大的水滴在电场力的作用下更容易发生变形和破碎，其临界变形度故而减小。此外，由图可知，600μm 粒径以下水滴在不同频率和占空比条件下的临界变形度曲线互有交叉，说明小粒径水滴临界变形度对电场变化的敏感性较小，当水滴粒径大于600μm 时，不同频率和占空比下水滴的临界变形度差值明显增大，即水滴粒径较大时，其临界变形度对电场变化的敏感性变大。

4 结 论

(1)随着水滴粒径的增大，水滴内外压差随之减小，抵御电场力变形的能力变小，变形度逐渐增大。当高压高频脉冲电场频率和占空比较高时，由于作用于水滴的电场能较大，水滴的振动变形幅度较大，从而使水滴粒径对液滴极化变形的影响更为明显；

(2)随着水滴粒径的增大，单个水滴变形度随之增加，两水滴相互极化引起的变形也随之小幅增加，在两者的叠加效应下，水滴平均变形度随粒径的增大而增大。另外，两水滴间的偶极聚结力随水滴粒径的增大而增大，使水滴相互靠近速率增加。由此看来，水滴粒径的增大有利于液滴的聚并；

(3)随着水滴粒径的增大，水滴附加压应力值减小，水滴更容易极化变形和破碎，水滴破碎的临界场强随之降低，水滴的临界变形度也随之变小。此外，外界电场发生改变时，大粒径水滴的临界变形度会产生较大变化。