断裂问题在路面工程中的研究进展
刘琬辰
(山东省交通规划设计院有限公司,山东 济南 250031)
引言
路面在使用过程中出现的各种各样的破坏问题中,开裂病害极具普遍性和严重性。由于裂缝尖端的特殊性,传统强度理论回答不了此类问题 ,而断裂力学提供了新的思路。与此同时,数值计算科学的发展填补了断裂力学对于复杂问题无法获得解析解的空白。两者相辅相成,促进了路面断裂的分析研究。
1 理论发展
路面开裂研究的理论基础是断裂力学。从断裂力学的确立到发展至今不到百年,基本可以归纳为三个阶段:线弹性断裂,疲劳断裂,弹塑性断裂[1]。20 世纪60 年代末、70 年代初断裂力学被引入路面研究中。
1.1 线弹性断裂
1.1.1 Griffith 理论和应力强度因子
1921 年英国科学家Griffith 最先从探究玻璃的实际强度的原因出发,提出脆性材料的断裂应力与材料裂纹尺寸有关,并用应变能释放率来表征裂纹扩展力。1957 年Irwin 针对具有含裂纹板,应用弹性理论解得各点应力分量,从表达式中提炼出与荷载和裂纹尺寸有关的的系数作为决定裂纹端部应力场强度的参量,称之应力强度因子K。
1.1.2 路面工程领域的线弹性断裂研究
20 世纪70 年代,Kauffman[2]将断裂力学的概念引入到路面结构的设计思想中,并用线弹性断裂理论预测路面开裂问题。随后的80 年代,Monismith[3]等人用线弹性断裂理论研究了基层反射裂缝裂缝问题,对加铺层的应力分布进行分析。Abdulshafi[4]等人使用盘状试件结合线弹性断裂的概念研究了沥青混合料的断裂问题[12]。
国内方面,周富杰[5]对旧水泥路面上沥青层罩面反射裂纹进行力学分析,认为裂纹尖端的应力强度因子KI,控制着裂纹初期的扩展,KII控制着裂纹后期的扩展。吴赣昌[6]对裂缝尖端的应力强度及其与路面温度分布和路面材料特性参数的关系进行了数值分析。
1.2 疲劳断裂
用什么参量来描述裂纹扩展,裂纹扩展的推动力是什么,这是疲劳裂纹扩展规律研究中最关键的问题。断裂力学是研究疲劳裂纹扩展的一个有用工具和常用方法。
1.2.1 Paris 疲劳寿命预测
1962 年,Paris 提出一个为工程界广泛采用的疲劳裂纹扩展速率的半经验公式:

式中:a—裂纹长度;N—荷载作用次数;C、n—材料常数;ΔK—应力强度因子幅值。成功地将应力强度因子,裂纹长度,荷载作用次数联系在一起。对公式积分可得到裂纹生长到指定长度时的寿命。
1.2.2 对Paris 公式的修正
Slowik 等人[7]结合混凝土的特性,提出在公式右边增添一个加项F(a, σ),表征混凝土裂纹在突加荷载情况下的力学响应,是与裂纹长度和突加荷载大小有关的函数。
Majidzadeh 等人[8]于1977 年将断裂力学原理应用于沥青混合料,总结出可用于沥青混合料的Paris裂缝扩展的一般形式:
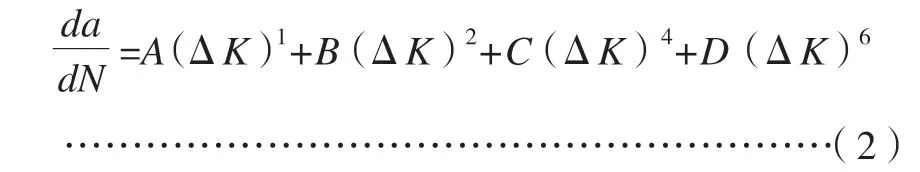
式中:A,B,C,D—材料断裂参数。
随后Schapery[9]对Paris 公式修正,描述黏弹性材料I 型裂缝扩展过程,只是式中的C 和n 有另外求解形式。
Jacobs[10]在Schapery 的理论上额外考虑沥青混合料的空隙和集料颗粒会影响裂纹扩展,提出参数的修正公式。
1.3 弹塑性断裂力学
材料在裂纹扩展前,端部都将出现塑性区,塑性区尺寸很小时,可以近似看成线弹性断裂问题。但当外荷载较大时,塑性区尺寸急剧增长,此时就需要弹塑性断裂理论加以研究。
1.3.1 J 积分
1968 年,针对弹塑性断裂问题,Rice 提出即J积分理论,考虑对任意一个围绕裂纹尖端的逆时针回路进行积分,巧妙地绕过裂缝端部复杂的应力应变场而获得弹塑性断裂问题中的裂纹力学参量。
1.3.2 内聚力模型
CZM(Cohesive Zone Model)是由Dugdale 和Barenblattt首先提出,自20 世纪70 年代起,CZM 被大量应用于水泥混凝土研究中,并逐步引入沥青混凝土领域。
CZM 将物理断裂区域限定在内聚力范围内,这个区域由两个虚拟的面所包围,界面上作用有内聚力。界面上的内聚力和界面的张开位移共同定义了内聚力区域的本构关系。对内聚力—位移曲线下的面积通过积分,可得到内聚力区域断裂能的计算公式,表述了材料的内聚关系。
国内有关研究[11]利用修正参数后的双线性CZM 模型,用数值模拟的方法,进行沥青混合料的劈裂试验,对比室内SCB 试的结果,进一步验证了双线性模型模拟沥青混凝土断裂行为的有效性,同时分析了试验过程中试件的应力分布和裂缝的形成与扩展。
1.3.3 沥青混合料的热粘弹性断裂
沥青混合料是典型的流变材料,其力学响应不仅依赖当前应力状态和环境温度,还与加载历史(黏弹性)和温变历史(热弹性)有关。
有关沥青混合料的黏弹性的本构模型经历了Maxwell 模 型、Kelvin 模 型、Burgers 模 型 和 广 义Kelvin 模型的发展过程。再依据时温等效性原理,可以将温变因素对材料力学性质的影响通过时间尺度来折算。
2 数值计算发展
2.1 有限元原理
有限元法是根据变分原理求解数学问题的一种数值计算方法。将实体经网格划分离散化,针对单元选定位移模式,结合几何方程、物理方程和平衡方程,再整合到整体,得到整个结构的平衡方程。

式中: [K]—整体刚度矩阵;{F}—荷载及边界条件;{δ}—未知应力。
在已知荷载作用条件下,考虑几何边界条件后,能够解出所有节点应力或位移(位移可以通过物理方程与应力联系)。
2.2 特殊单元
裂缝尖端奇异性决定了裂缝尖端附近采用的由参单元退化以后可得到奇异单元而非常规单元,该单元退化边为裂缝前端,并将中间结点移至靠近裂缝尖端1/4 单元边长时即可满足裂缝尖端的奇异性。
在考虑路面面层受到汽车制动或启动产生的水平力时,采用表面效应单元可以将作用在其上的荷载转化为均布荷载作用,从而模拟实际中路表面受到水平均布荷载的作用情况。
利用数值计算方法模拟路面结构中的夹层,常常通过将夹层材料近似成具有一定厚度的弹性材料;或是采用薄膜单元和界面单元,分别表征夹层材料和层间接触情况。两种单元各自有相应的刚度矩阵,形函数和坐标转换矩阵。
2.3 热黏弹性断裂的有限元计算
热黏弹性本构关系(采用时间增量型本构关系)引入到对沥青面层的描述中,一般考虑采用:
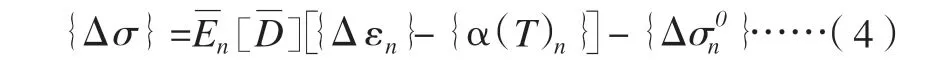
2.4 传统裂纹扩展过程的模拟
对传统的裂纹扩展,一般思路是借助有限元软件对外荷载作用下的裂纹端部进行应力场分析,判断失稳扩展条件:

式中:K*—混合型应力强度因子;KIC—断裂韧度,由试验测得;θ*—扩展角,由方程解得:
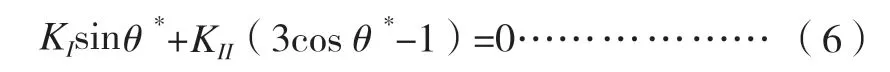
沿该方向对裂缝长度增加,Δα并再次计算裂纹的应力场,依此思路逐步模拟裂纹扩展过程[12-13]。其间需克服的困难是裂纹扩展过程中的网格不连续问题。
2.5 扩展有限元与广义有限元
扩展有限元与广义有限元是近十年来处理裂缝问题的先进技术。两者的核心思想是一致的[14-15],不同之处仅限于单元结点处自由度的物理涵义不同,所采用的数值积分技术也不同。在利用广义有限元和扩展有限元处理路面开裂问题时,两者的差异并不会影响结果。
总体来说,GFEM 和XFEM 在模拟路面结构裂缝问题方面的优势明显:(1)网格划分不依赖结构体,极好地解决了裂缝区域的网格划分问题。(2)智能化全程化地模拟扩展路径,包含了裂缝萌生和扩展的全过程。
Hasan Ozer[16]以断裂力学为基础,以广义有限元为手段,利用高次等效区域积分法对柔性路面裂缝的宏观参量进行计算,评价分析了路面模型中的60 种不同裂缝的应力状态和扩展路径。国内有相关人士利用扩展有限元分析了路面反射裂纹的断裂问题[17]和路表面自上而下裂纹的二维扩展[18]。
3 结语
基于断裂力学的黏弹性力学方面的应用研究工作主要集中在沥青混合料的黏弹性及低温抗裂指标的实验研究及沥青路面温度应力计算方面,应用黏弹性断裂力学理论与方法进行理论分析方面的工作尚待扩充。
到目前为止,基于断裂力学的路面开裂缝问题的研究基本限于静态加载或缓慢加载下的裂纹扩展问题。对于重载比例扩大化,涉及到与时间有关的裂纹快速起裂、扩展或止裂问题等属于动态断裂力学范畴的研究将更加广泛。

