UTM投影和高斯投影的比较
陈鑫

摘 要:本文主要是针对在日常的测量工作和工程建设施工中我们所经常用的两种投影方式,并且分别对这两种投影方式各自进行了详细的阐述和比较,在我们国内的工程测量和建设施工中基本都是采用的高斯投影方式,然而在国外的大多数地区和国家却是采用的UTM投影方式,我然后接着再引入高斯投影和UTM投影相互转换的实际的例子。最后并介绍上述两种投影方式在低纬度地区的情况,并最后结合相应的实验数据和结果来进行探讨。
关键词:高斯投影;UTM投影;投影变形;地球椭球体;重采样;高斯正算;高斯反算
1 概述
在最近几个世纪以来,人们陆陆续续的发明了各种各样的投影变换的算法,比如面的投影方法、线的投影方法和角度的投影方法等等,但是各种投影方式都有其优缺点。它们都无法保证方向、角度、长度和面积等同时的不走样,基本上只能顾及其中的一部分而尽力的抑制其他部分的失真[1]。另外,我们国内在对UTM投影和高斯投影原理的理解上往往有些偏差,在投影变换使用上也还有些差距,本文在此试图对此进行简单的探讨。
2 研究数据与研究方法
2.1 研究数据
为了保证数据的准确性和可靠性进而使得得到的结果更具有说服力,此次的实验数据来源于地理空间数据云的官方网站(http://www.gscloud.cn/)。首先,由于我国的原始遥感卫星资料常常采用UTM投影,而最终的数据成果都将统一到国家2000坐标中,故此处讨论UTM投影向高斯投影的转换,其数据为美国陆地卫星的中国地区影像图。
2.2 研究方法
2.2.1 高斯投影与UTM投影基于ArcGIS的相互转换
在全国三调实际工作中,国家会统一下发已经制作做好的工作底图,也就是说是经过投影变换的,所以我们在实际工作中不需要地方再去进行投影变换。若原始影像资料是没有经过投影变换的,我们可以参照以下方法进行投影变换。步骤如下:第一步,数据准备(原始影像资料)。第二步,软件准备(软件选用投影类型较为全面的ArcGIS软件中的ArcMAP组件)。第三步,操作步骤(以影像资料为例进行投影变换。
2.2.2 高斯投影与UTM投影的变形
高斯投影后的中央经线的比例为K=1,而UTM投影后的中央经线比例K=0.9996。进而导致两种投影在地球表面上的水平距离ρ、高程面长度投影等等方面存在不一样,当我们所要研究的区域高差较大时,此时我们应加入改正,补偿长度变形的量[7],计算过程:
从而我们可以得知,根据投影的规则,地面水平距离ρ的长度总变形Δρ为:Δρ=Δρ1+Δρ2。
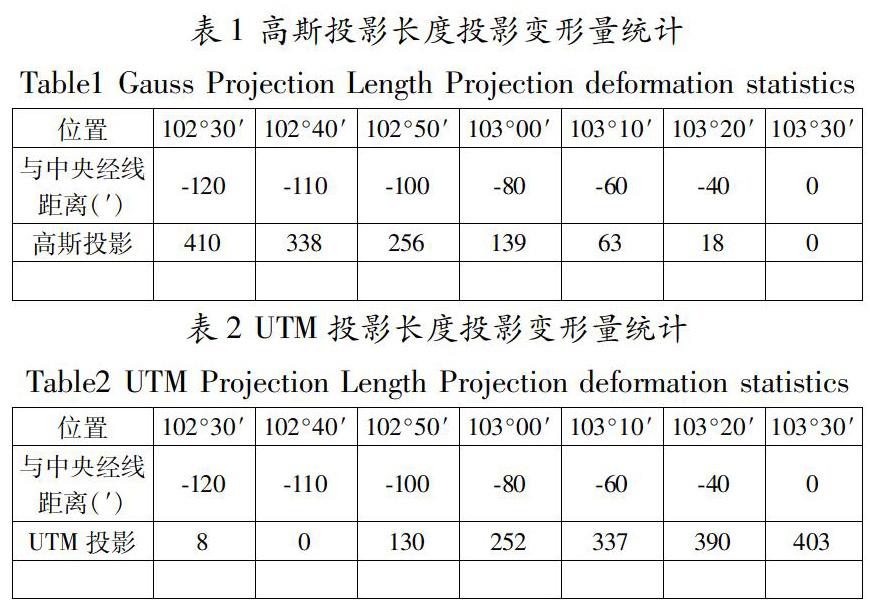
对于投影变化的量的减少方法[7],基本上都是采用选择与工程实际情况相适应的投影高程面与投影分带的方法,根据GB50026—2007《工程测量规范》3.1.4的规定:平面控制网的坐标系统,测区内的投影长度变形应满足不大于2.5cm/km[8],其所遵循的原则:当投影后改化的数据效果不太理想时,可以尝试通过建立该地的独立坐标系,从而满足工程施工精度的要求。用excel上述数据导入,用excel内带公式计算[9]。绘制成表格如下图所示。
3 研究结果分析
如上图所示,将表1和表2UTM的数据导入Excel并利用其制图功能做成该曲线图,从该图中我们可以得到许多关于高斯投影与UTM投影的变形信息。
首先,对于高斯投影。在中央子午线两侧经度各小于40°左右,其长度变形小于限差。在两侧各大于40°时均超过限差,说明该投影区域的高斯投影不满足精度要求。
最后,对于UTM投影。在中央子午线两侧经度各小于110°左右,其长度变形大于限差,说明该投影区域的UTM投影不满足精度要求。
4 结论
(1)UTM投影中的中央经线投影前后的比例因子K的数值对实际的工程建设十分关键,这就提醒我们国内的测量工作人员在使用国内传统的测量方法要去国外施工的时候要特别小心注意,在小区域内的工程施工中可能是不容易的看出来,由于在我们国内的长期经验我们测量工作人员很可能会将其原因归结到控制点精度不高,然而这对于大区域的测量工作就会带来非常非常严重的错误。
(2)中国国内所采用的高斯投影与UTM投影虽然或多或少的存在一定的差异,但是我们的测量人员只要掌握和了解其特性,同样也就可以加以解决其变形的严重问题。UTM与高斯两者对比来看,两者的长度L和面积S的变形以及投影后分带的方式是非常非常的相似。上文最后对于高斯投影和UTM投影的基本原理分别进行了阐述和比较。对于在实际的测量工作中,还必须要结合具体的实际情况和测区的精度要求来选择何种的投影方式。
参考文献:
[1]周朝宪,房志峰,于彩虹,等.UTM投影和Gauss-Kruger投影及其变换实现[J].地质与勘探,2013,49(5):882-889.
[2]孙皓,闫静,武清华.高斯—克吕格投影与UTM投影的差异及转换[J].西部资源,2014(1):206-207+209.
[3]孙立东.高斯-克吕格投影和横轴墨卡托(UTM)投影的异同[J].港工技术,2008(5):51-53.
[4]欧龙,陈性义,欧阳平.高斯投影正反算与换带计算TrueBASIC程序[J].铁道勘察,2006(5):12-15.
[5]石全喜,王宗强,陈磊杰.UTM投影变形分析及工程应用[J].住宅与房地产,2019(27):217+222.
[6]陆佳伟.UTM投影和高斯-克吕格投影及其变换实现[J].交通世界(工程技术),2015(4):72-73.
[7]赵鑫,尹伟言,张小莉,陈衡军.改进的高斯投影在城市测量中的应用[J].地理空间信息,2018,16(6):78-80+8.
[8]贾登科,麦若绵,朱国锋.欠发达国家坐标系统及平面控制有关问题探讨[J].水运工程,2013(7):122-126.
[9]谷超杰.Excel 2003在高斯投影坐标换算中的应用[J].测绘与空间地理信息,2008,31(6):190-192.
[10]高德章.大地坐标系与投影坐标系[J].物探化探计算技术,2011,33(1):51-55+119.
[11]刘健,卢加华,杨新云,等.中纬度地区兰勃特投影和高斯-克吕格投影变形分析[J].地矿测绘,2019,35(3):12-14+17.
[12]温珍灵.基于CGCS2000的高斯投影面积变形研究[D].贵州师范大学,2016.
[13]赵国强.几内亚BOFFA铝土矿开发UTM投影坐标系的建立[J].资源信息与工程,2018,33(6):136-137.
[14]倪卫明,杨月军.UTM投影在国外低纬度地区的应用[J].硅谷,2014,7(7):116+108.
[15]叶达忠.国际工程测量的UTM投影变形及抵偿分析[C].中国测绘学会.中国测绘学会第九次全国会员代表大会暨学会成立50周年纪念大会论文集.中国测绘学会:中国测绘学会,2009:886-888.
[16]廉保旺,张怡,李勇,昝積成,赵乃煌.UTM坐标转换成大地坐标系的算法研究[J].弹箭与制导学报,1999(3):15-19.

