基于SAC算法的机械臂控制方法与分析

王骏超

摘 要：机械臂作为一种常见的自动化设备，关于其控制算法的研究，一直是相关领域的热点。本文结合目前比较热门的人工智能理论，将强化学习方法引入到机械臂控制中，提出一种基于Soft Actor-Critic Algorithms算法的控制策略，以更好地解决三维空间下多轴机械臂的轨迹规划问题。利于CoppeliaSim平台，搭建仿真环境，选择UR5机械臂作为实验对象，进行了多组对比实验。结果表明：基于策略熵最大化的SAC算法，提高了训练样本利用率，保证了学习结果的最优。在用于三维空间中多轴机械臂控制任务时，不仅可以克服传统控制算法存在的模型依赖性高，规划精度低的不足，并且相比一般强化学习算法，具有更快的学习效率和更高的稳定性，轨迹也更为平滑，具有很好的实用价值。

关键词：机械臂控制;SAC算法;轨迹规划;强化学习

中图分类号：TP242  文献标识码：A  文章编号：1673-260X（2020）10-0033-07

1 引言

机械臂是一种最常见的也是最早出现的自动化设备，关于其控制算法的研究一直是业内关注的焦点[1，2]。目前比较常见的机械臂轨迹规划方法主要包括A*算法、人工势场法、快速扩展随机树算法等。A*算法是一种典型的启发式搜索（Heuristically Search），一直受到广泛的研究[3]，但是A*算法的估价函数构造往往需要人工经验尝试，影响了规划的稳定性和精度。人工势场法具有良好的实时性[4]，但会出现局部最优或振荡不收敛的情况，在环境比较复杂或者机械臂自由度较高时，不能保证规划的稳定性和可靠性。快速扩展随机树法理论简单且容易实现[5]，当参数设置合理时，可有效避免出现局部最小值的情况。但是所得到的轨迹曲线比较粗糙，往往并不是最优[6]，算法的效率较低，并且重复性较差，控制效果不稳定[7]。因此，传统的轨迹规划算法在解决机械臂控制问题时均存在着效率低、稳定性差、模型依赖性高的缺陷。

将强化学习算法理论与机械臂运动轨迹规划控制问题相结合，可以有效弥补和改善传统算法存在的不足。并且，随着研究的深入也出现了一些成功的案例，例如：Peters J等人在2006年利用强化学习方法使7自由度的SARCOS Master机械臂完成挥棒击球的任务[8];2011年，Durrant-Whyte H利用一个桌面级机械臂和深度摄像头[9]，通过强化学习的方法使其完成了空间积木块的堆叠任务;Mulling K和Kober J等人在2013年以学习打乒乓球为例，介绍了一种机器人通过与人的物理交互来学习的新框架[10];Gu S等人在2017年提出一种基于深度Q函数离线训练策略的深度强化学习算法，通过多台机器人并行学习来训练真实的物理机器人执行复杂的三维操作任务[11]。虽然强化学习算法比较适合应用于机械臂的运动控制，但是，不同类型的强化学习算法在实际使用时还存在着一些问题：

（1）On-policy类强化学习算法的样本效率低下。例如，目前主流的用于连续控制的深度强化学习（DRL）：TRPO算法，PPO算法和A3C算法在每执行一步都需要收集新的样本[12]，因此所需的步骤数和样本量会随着任务复杂性增加而增加，即使是相对简单的任务也可能需要数百万个数据收集步骤，而具有高维度的复杂任务可能需要训练一天甚至几天的才能收敛，成本高昂。

（2）对于基于Q-learning（QL）类的强化学习算法来说，提高样本效率，复用先前经验是相对容易的[13]。但是，其离散的状态空间在处理连续控制问题时可能会导致维数灾难（Curse of Dimensionality）。通过连续状态离散化的方式进行机械臂的动作控制，往往稳定性和收敛性都无法保证。

（3）另一类Off-policy算法，如深度确定性策略梯度算法（deep policy gradient， DDPG）[14]，相比QL算法更适合解决连续控制问题，相比PPO等算法也有更高效的样本学习。但是，DDPG算法在面对高维任务时，Actor网络与Q网络的相互影响造成了算法的脆弱性和超参数敏感，这严重限制了在现实任务中的适用性，甚至需要依靠精确的建模，才能实现对真实机械臂的有效控制[15]。

针对目前常用算法在用于多轴机械臂控制时存在的一些不足和问题，本文提出了一种基于柔性角色行为评价算法（Soft Actor-Critic Algorithms，SAC）[16]的机械臂控制方法，并且在CoppeliaSim平台上搭建了UR5多轴机械臂的仿真环境，进行多组对比实验予以验证。

2 SAC算法

Soft Actor-Critic Algorithms是一种基于最大化熵理论的无模型深度学习算法，同时具备了Actor-Critic算法框架。不同于确定性策略（Deterministic Policy）算法，SAC算法的主要特征是策略随机化（Stochastic Policy）。经过训练，尽可能地在收益和熵（即策略的隨机性）之间取得最大化平衡。这就是使探索与决策的关系非常密切：熵的增加会使智能体倾向于探索更多的情况，从而可以加快后续的学习速度。同时策略的随机性还可以避免出现过早收敛到某个局部最优值。

2.1 熵最大策略

最大熵原理最早是在信息论中提出的[17]，目的是为了让获取的数据足够随机分散。这样的思想同样可以用在强化学习中。使用最大熵原理的强化学习，除了要实现价值最大的目标，还要求策略？仔选择的每一次动作的熵（Entropy）最大，如式（1），其中st，at为t时刻的状态和动作，R为得到的奖励，H为熵函数，？琢为温度参数，用于控制优化目标更关注奖励还是熵。

3 实验部分

3.1 实验仿真平台

选用CoppeliaSim进行实验仿真。CoppeliaSim具有完善的集成开发环境，是非常理想的机器人仿真建模的工具。用于实验的机械臂为Universal Robots公司的优傲机械臂UR5。UR5是一种高自由度的机械臂，更能验证本文算法在多轴复杂的真实机械臂中的性能表现。其机械臂坐标系如图3，D-H参数如表1。

根据UR5的数据，在仿真平台CoppeliaSim中配置出UR5的3D可视模型，如图4。

3.2 实验设计

选用UR5的第一关节Joint 1到第四关节Joint 4的角度作为控制变量，关节Joint 5和Joint 6是控制末端执行控制器精细位姿，在实验过程中固定角度，通过其他四个关节角度改变来实现控制。SAC算法状态输入量为机械臂UR5的四个关节角度以及目标点坐标，即：

3.3 对比实验一

在上述仿真环境中，验证SAC算法用于机械臂控制的性能表现，并用深度确定性策略梯度算法（DDPG）作为对比实验。

DDPG算法是常见的用于解决连续空间规划问题的强化学习算法。与SAC算法最大的不同，是其策略的更新梯度是固定的。并且由于结合了DQN算法的思想，DDPG算法中具有四个网络（现实策略网络、目标策略网络、现实Q网络、目标Q网络）。为了确保实验结果的可靠性，DDPG算法的参数设置与SAC算法基本保持相同。

最大训练回合数设置为3000，每回合最大步数为100，当超过100步仍未到达目标点，则结束此次训练回合，训练流程图如图6：

选择平均奖励变化和成功率变化两个指标作为对比标准。

图7是机械臂UR5在有障碍物的环境中，分别使用SAC算法和DDPG算法得到平均奖励曲线。图中绿色点线图代表SAC算法，黄色点线图代表DDPG算法。图7可以反映出UR5经过两种强化学习算法训练后，执行每步动作得到的平均奖励的变化情况。

从图7可以看出，SAC算法和DDPG算法训练后期均稳定在-10左右，说明两个算法在机械臂避障实验中均可以有效地控制UR5机械臂到达目标点，但是DDPG算法直到14000步左右平均奖励值的变化才趋于稳定，慢于SAC算法，说明在三维空间的规划任务中，DDPG算法的样本效率和速度是低于SAC算法的。同时，DDPG的平均奖励曲线变化的幅度是大于SAC算法的，为了保证对比实验的客观可靠，DDPG直接采用了与SAC算法基本一致的参数设置，而没有进行专门的调参，可见在算法稳定性方面，DDPG低于SAC算法。

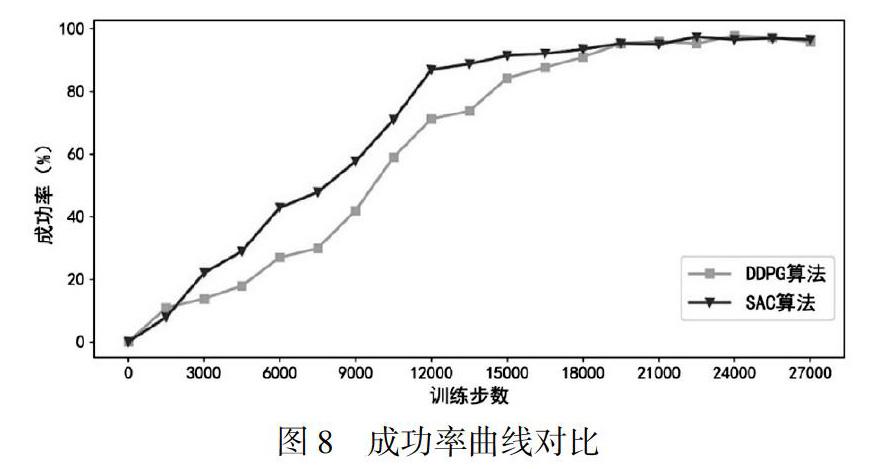
按照阈值条件：||Parm-Ptarget||≤2.5时机械臂规划成功，统计出基于SAC算法和DDPG算法的机械臂UR5的避障控制成功率曲线。图8中，绿色带倒三角曲线是SAC算法的成功率，黄色带正方形曲线是DDPG算法的成功率。

图8中SAC算法和DDPG算法的成功率曲线与平均奖励曲线的趋势基本相同。SAC算法在18000步左右达到了96%以上的成功率，相比较之下，DDPG算法在20000步之后成功率才稳定在相同水平。从成功率变化曲线的对比中，也可以说明SAC算法的速度是快于DDPG算法的。

3.4 对比实验二

在相同的仿真环境中，选择传统算法中的RRTstar算法，比较在相同环境下两种算法的规划效果。RRTstar算法是一种应用比较广泛的避障算法。相比较一般的RRT算法，具有渐进最优性，而且规划速度也比较快。RRTstar作为一种基于随机树策略的算法，与SAC算法原理上是不同的。因此，不同于第一组对比实验，在本组实验对比中，分别选择机械臂轨迹规划路径代价（长度/用时）和关节角度变化曲线作为两个对比标准。

RRTstar避障算法的规划流程示意图如图9。

表4是RRTstar算法的参数设置，迭代次数超过1000次则此次规划任务失败;γ是常量系数，影响每次取球状节点集合的半径大小;d是规划空间维度;δ是步长（单位cm）。

首先把RRTstar算法运行十次，统计其规划的结果，规划路径代价用轨迹长度和规划用时表示。

作为比较，在同一环境中使用SAC算法进行避障控制实验。为了保证对比实验的可靠性，初始化SAC算法的经验重播缓冲区，再次进行训练。SAC算法的其他参数设置不变，最大训练回合数设置为3000，每回合最大步数为100。训练结束后，用所得的模型进行UR5机械臂的避障规划。同样规划十次，统计其结果，如表6。

从表7和图10对比中可得，在十次规划中，相比于RRTstar算法，使用SAC算法得到的轨迹路径长度比较稳定，与平均长度接近，并且平均长度更小。SAC算法规划的平均用时只有7.9秒，远远小于RRTstar算法39.48秒的平均时间。此外，RRTstar的规划用时的波动幅度较大，说明在控制机械臂执行同一任务时，基于随机策略的RRTstar算法的重复稳定性较差。十次规划中，SAC算法均可以使机械臂成功到达目标点，成功率高于RRTstar算法。综上所述，从规划路径长度，规划用时以及成功率三个方面的对比，均说明了SAC算法相比于RRTstar算法性能更加优越，更适用于多轴机械臂三维空间的避障控制。

图11展示了从RRTstar算法和SAC算法十次规划中，各取一次的规划轨迹对比图。图12是RRT算法和SAC算法控制UR5机械臂进行避障时的关节角度变化对比图。

图11表明：二者的规划轨迹的长度比较接近，最后到达目标点存在一定的误差，但是都达到了规划要求。但是相比于RRTstar算法，SAC算法的规划轨迹更加平滑，角度变化的幅度和突变较小。图12表明：在分别使用RRTstar算法和SAC算法规划时，UR5机械臂的关節角度变化范围相近，但是SAC算法的角度变化更加平缓，突变较少。这说明RRTstar算法用于机械臂控制时存在着规划路径粗糙的短板，而SAC算法规划路径更加平滑。这在应用于真实机械臂控制时，能够减少机械臂的自身磨损，延长使用寿命，有利于提高规划控制的经济性和安全性。

4 结论

本文通过研究分析机械臂控制模型和强化学习的相关理论;结合机械臂控制的特点和常见控制算法存在的不足，提出了基于柔性角色行为评价算法（Soft Actor-Critic Algorithms，SAC）的机械臂控制方法。利用SAC算法处理连续动作与状态空间任务的优越性能，提高了训练的效率和稳定性。为了验证本文方法用于真实机械臂规划控制的实际效果，选用CoppeliaSim作为实验平台，UR5机械臂作为实验对象。比较了SAC算法与DDPG算法、RRTstar算法在相同环境下的性能表现。选取不同的评价指标均表明SAC算法相比于DDPG算法速度更快，稳定性更高;相比RRTstar算法规划的轨迹更加平滑，机械臂关节角度不会突变，并且速度和成功率更高。由此说明，本文提出的基于SAC算法的机械臂控制方法可以有效弥补传统控制算法的不足，具有一定的自身优势和较好的应用价值。

参考文献：

〔1〕冯旭，宋明星，倪笑宇，等.工业机器人发展综述[J].科技创新与应用，2019，9（24）.

〔2〕Schaal， Stefan. The new robotics towards human-centered machines[J]. Hfsp Journal， 2007， 1（02）：115-126.

〔3〕Schaal， Stefan. The new robotics towards human-centered machines[J]. Hfsp Journal， 2007， 1（02）：115-126.

〔4〕Khatib O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots[J]. 1986.

〔5〕Lavalle S M. Rapidly-Exploring Random Trees： A New Tool for Path Planning[J]. Algorithmic & Computational Robotics New Directions， 1998： 293-308.

〔6〕Lindemann S R， Lavalle S M. Current issues in sampling-based motion planning[J]. Springer Tracts in Advanced Robotics， 2005， 15： 36-54.

〔7〕王濱，金明河，谢宗武，等.基于启发式的快速扩展随机树路径规划算法[J].机械制造，2007，58（12）：13-16.

〔8〕Peters J， Schaal S. Policy Gradient Methods for Robotics[C]// Intelligent Robots and Systems， 2006 IEEE/RSJ International Conference on. IEEE， 2006.

〔9〕Durrant-Whyte H， Roy N， Abbeel P. Learning to Control a Low-Cost Manipulator Using Data-Efficient Reinforcement Learning[C]// Robotics： Science and Systems VII. MIT Press， 2011.

〔10〕Mulling K， Kober J， Kroemer O， et al. Learning to select and generalize striking movements in robot table tennis[J]. The International Journal of Robotics Research， 2013， 32（03）： 263-279.

〔11〕Gu S， Holly E， Lillicrap T， et al. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates[C]// 2017 IEEE International Conference on Robotics and Automation （ICRA）. IEEE， 2017.

〔12〕Schulman， John， Wolski， Filip， et al. Proximal Policy Optimization Algorithms[J].2017.

〔13〕Mnih， V.， Kavukcuoglu， K.， Silver， D.， Rusu， A. A.， Veness， J.， Bellemare， M. G.， Graves， A.， Riedmiller， M.， Fidjeland， A. K.， Ostrovski， G.， et al. Human-level control through deep reinforcement learning[J]. Nature， 2015， 518（7540）： 529-533.

〔14〕Lillicrap T P， Hunt J J， Pritzel A， et al. Continuous control with deep reinforcement learning[J]. computer science， 2015， 8（06）： A187.

〔15〕Duan Y， Chen X， Houthooft R， et al. Benchmarking Deep Reinforcement Learning for Continuous Control[J]. 2016.

〔16〕Haarnoja， Tuomas， Zhou， Aurick， Hartikainen， Kristian， et al. Soft Actor-Critic Algorithms and Applications[J]. arXiv preprint arXiv， 2018：1812.05905.

〔17〕冯尚友.信息熵与最大熵原理[J].水利电力科技，1995，24（03）：26-31.