海南省松树、橡胶树削度方程模型研建

胡 开，贺 鹏，龙圣智，聂 峰

(1.西藏自治区林业调查规划研究院，拉萨 850000；2.国家林业和草原局中南调查规划设计院，长沙 410014)

削度方程是指树干上部任意部位的直径为该干径位置距地面高、全树高及胸高直径的函数。它的主要功能是估计树干任意高度处的直径、计算树干总体材积、计算从任意伐根至任意小头直径的商品材积和长度、推算各段原木的材积[1]。因此，削度方程在林业生产中应用相当广泛。

从削度方程的研究历史阶段来看，大致可以分为4个阶段[2]：第一阶段，20世纪50年代以前，主要采用图解法绘制干形和削度曲线，以此来描述树干削度变化情况；第二阶段，20世纪60年代以后，随着计算机在林业研究中的普及，有效地解决了削度方程拟合的计算问题，使建立更加复杂的模型结构成为可能(如四次多项式结构)；第三阶段，20世纪70年代，削度方程的研究进入了一个新阶段，提出了一致性削度方程、分段多项式回归模型等新概念；第四个阶段，20世纪80年代后，削度方程的种类层出不穷，提出了以树木生长方程为基础，建立树干削度方程和可变参数的削度方程模型等新思想。经过这四个阶段的发展，无论削度方程的理论研究，还是实际应用都取得了长足的发展，为各材种出材率表的编制打下了坚实的基础。

本文以海南省松树、橡胶树为研究对象，采用当前最为常用的削度方程模型结构，分别建立固定参数削度和可变参数削度方程模型，以期为编制海南省松树、橡胶树单株立木材种出材率和林分出材率表提供科学依据。

1 样本收集与处理

为保证模型的适用性，在样本组织方面，采集范围尽可能覆盖海南省各个地区，同时尽可能扩大样本变量(胸径、树高)的覆盖范围，以期真实反映变量间相关规律的完整性、真实性和稳定性。为此，松树和橡胶树的取样范围，按胸径分为6，10，16，22，28cm和32cm以上共6个取样点位；在每点位取样时要求尽量按树高的实际变化范围分低、中、高(以高径比控制)选取样木；伐倒后分0，0.5/10，1/10，2/10，3/10，4/10，5/10，6/10，7/10，8/10和9/10树高处实测带去皮直径。用区分求积法计算出样木的带皮和去皮材积。

因为削度方程的建模数据包括各个相对高度处的直径，数据量较多，首先分径阶按3倍标准差剔除，然后做不同高度处的直径与相对树高的散点图，对散点图进行分析，在散点图上对反映特别异常的数据进行剔除，最终形成松树和橡胶树建模样本资料，具体建模样本数据详见表1。同时，独立收集53株检验样本数据，用于对模型进行检验评价。

表1 削度方程建模数据树种 变量样木数平均值最大值最小值标准差变异系数/%松树胸径/ cm16219.844.905.5010.452.5树高/ m16213.626.703.585.741.9橡胶树胸径/ cm16219.545.005.4010.151.8树高/ m16215.324.655.305.234.0

2 研究方法

2.1 模型结构设计

对目前国内外已公开发表的数十种削度方程进行理论分析和比较，从中选出2个最佳结构式[3]：

(1)

(2)

式中：D为胸径，H为全树高，h为树干基部至树梢方向的高度，d为在树干h高处的直径，Z为相对树高 (h/H)。

将上述削度方程统一转换为结构通式：d=f(D,H,h)后再进行拟合。

2.2 异方差处理

由于林业数表通用回归模型中常存在异方差现象，在利用非线性回归方法进行拟合时，还需要采取适当措施以消除异方差的影响[4-5]。常用的方法有对数回归或者加权回归，本文均采用非线性加权回归的方法。关于权函数的选择，削度方程模型权函数均采用其模型本身。

2.3 模型评价

2.3.1 统计指标

用6个指标来对模型进行评价和检验。R2(确定系数)，SEE(估计值的标准差)，TRE(总相对误差)，MSE(平均系统误差)，P(预估精度)和MPSE(平均百分标准误差)，其计算公式如下：

(3)

(4)

(5)

(6)

(7)

(8)

2.3.2 模型参数稳定性评价

参数稳定性是判定一个模型是否可用的重要指标，一般以参数变动系数不超过±50%为识别标

准[6]。拟合效果好的模型要求参数稳定(参数估计值的t值大于2或变动系数<50%)。

2.3.3 残差随机性检验

为了更直观地检验模型的全面切合性能，应利用标准残差对自变量作残差分布图，对残差分布的随机性进行判断，残差应均匀随机分布(各阶径的残差正负相抵，以0为基准线上下对称分布)[6]。

3 结果分析

3.1 模型拟合结果

按照非线性加权最小二乘法进行模型拟合，权函数为模型本身。松树和橡胶树带皮削度方程模型和去皮削度方程模型的拟合结果见表2和表3。

表3 去皮削度方程模型拟合结果树种模型C0C1C2C3参数值变动系数参数值变动系数参数值变动系数参数值变动系数松树可变参数1.505 6883.53-3.433 9593.942.479 6933.800.209 1543.35固定参数0.728 1790.47橡胶树可变参数2.091 4634.92-3.126 4558.021.496 45311.060.374 5253.09固定参数0.886 8950.55树种模型统计指标R2SEEP/ %MPSETREMSE松树可变参数0.988 50.951 45499.676.40.560.28固定参数0.977 51.333 13799.548.782.923.05橡胶树可变参数0.966 71.679 16199.5910.830.080.02固定参数0.935 72.331 97899.4314.12-0.630.84

从表2和表3 可知，松树和橡胶树两个树种带皮或去皮削度方程的拟合结果都很好，确定系数基本上都在0.93以上，预估精度在99.0%以上，模型均具有较小的标准误差、稳定的模型参数，且可变参数模型要优于固定参数削度方程。

3.2 模型检验

削度方程作为通用性预估模型，仅采用上述统计指标进行整体评价尚不足以充分辨识所建模型的效果，还须进行残差随机分布检验，以及分整体、分相对树高计算总相对误差(TRE)和平均系统误差(MSE)2个统计指标，以检验模型是否具有良好的切合性能。

3.2.1 模型残差随机性检验

模型的残差是否随机，对于保证模型的通用性是至关重要的。为此，采用削度方程残差随直径和相对树高变化的残差分布图，以此来检验模型的通用性，由于篇幅原因，本文只列出了松树模型的残差分布图(图1和图2)。结果表明，松树和橡胶树的可变参数削度方程明显优于简单削度方程，残差呈随机分布，不存在明显的系统偏差；固定参数削度方程在相对树高为0的范围内存在明显的系统偏差。

3.2.2 利用检验样本对模型检验

利用检验样本，分整体和相对树高，采用TRE和MSE两个指标对模型的切合性能进行检验。从表4可知，对于松树，无论是带皮削度方程，还是去皮削度方程，在整体上均无明显系统偏差，可变参数模型要优于固定参数模型。在各相对树高处，可变参数模型的TRE和MSE除了在0.8H和0.9H处超出±5%以外，其它各相对树高处均在±5%以内；固定参数模型在0和0.9H处存在明显偏差外，其它各相对树高处TRE和MSE基本上都在±5%以内。

从表5可知，橡胶树无论是带皮削度方程，还是去皮削度方程，在整体上均无明显系统偏差，可变参数模型要优于固定参数模型。在各相对树高处，可变参数模型的TRE和MSE除了在0.8H和0.9H处超出±5%以外，其它各相对树高处均在±5%以内；固定参数模型除了在0处存在明显偏差外和0.7H处TRE达到10%，其它各相对树高处TRE基本上在±8%以内。

图1 松树可变参数带皮和去皮削度方程残差分布图

图2 松树固定参数带皮和去皮削度方程残差分布图

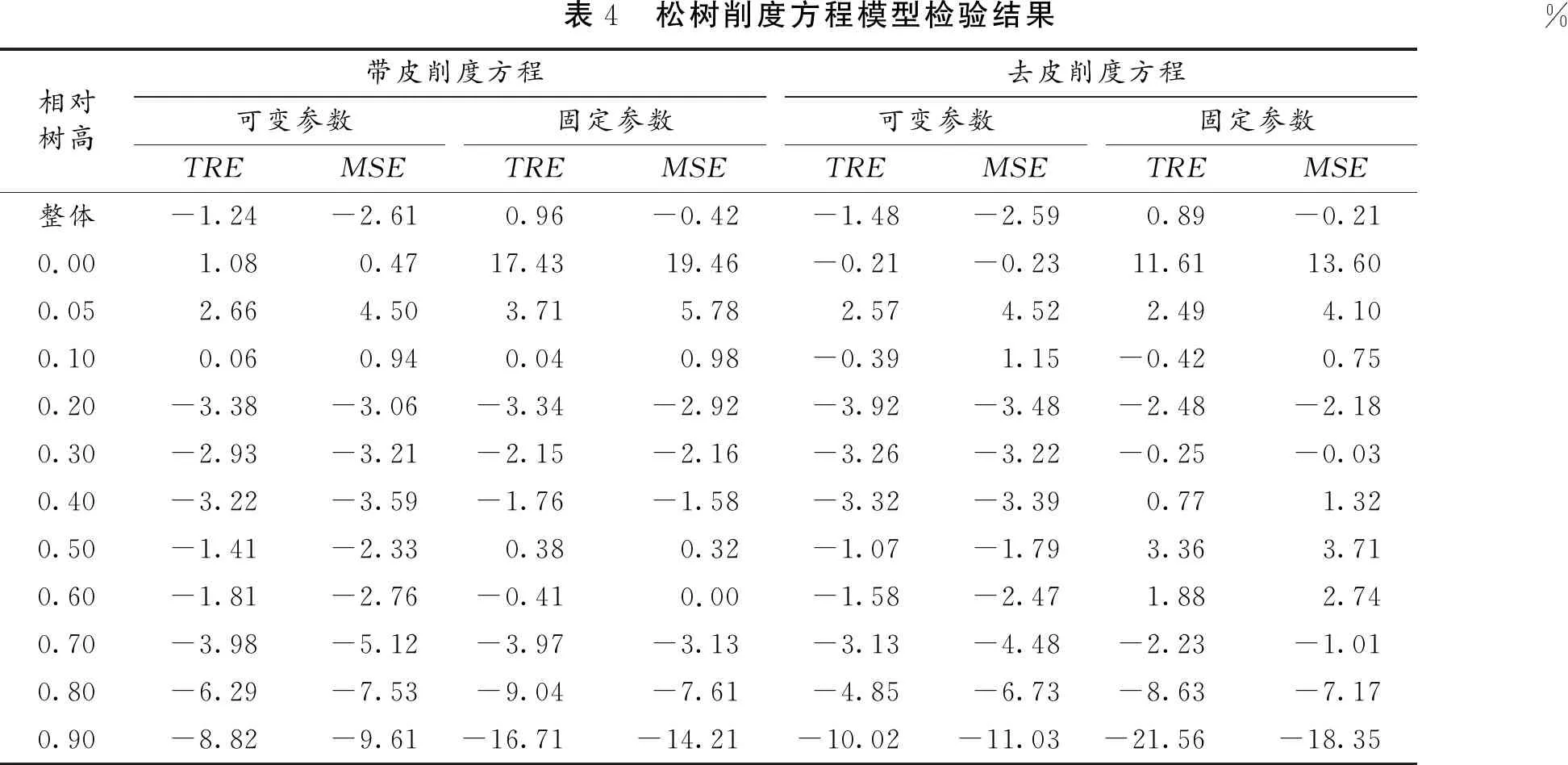
表4 松树削度方程模型检验结果%相对树高带皮削度方程去皮削度方程可变参数固定参数可变参数固定参数TREMSETREMSETREMSETREMSE整体-1.24-2.610.96-0.42-1.48-2.590.89-0.210.001.080.4717.4319.46-0.21-0.2311.6113.600.052.664.503.715.782.574.522.494.100.100.060.940.040.98-0.391.15-0.420.750.20-3.38-3.06-3.34-2.92-3.92-3.48-2.48-2.180.30-2.93-3.21-2.15-2.16-3.26-3.22-0.25-0.030.40-3.22-3.59-1.76-1.58-3.32-3.390.771.320.50-1.41-2.330.380.32-1.07-1.793.363.710.60-1.81-2.76-0.410.00-1.58-2.471.882.740.70-3.98-5.12-3.97-3.13-3.13-4.48-2.23-1.010.80-6.29-7.53-9.04-7.61-4.85-6.73-8.63-7.170.90-8.82-9.61-16.71-14.21-10.02-11.03-21.56-18.35

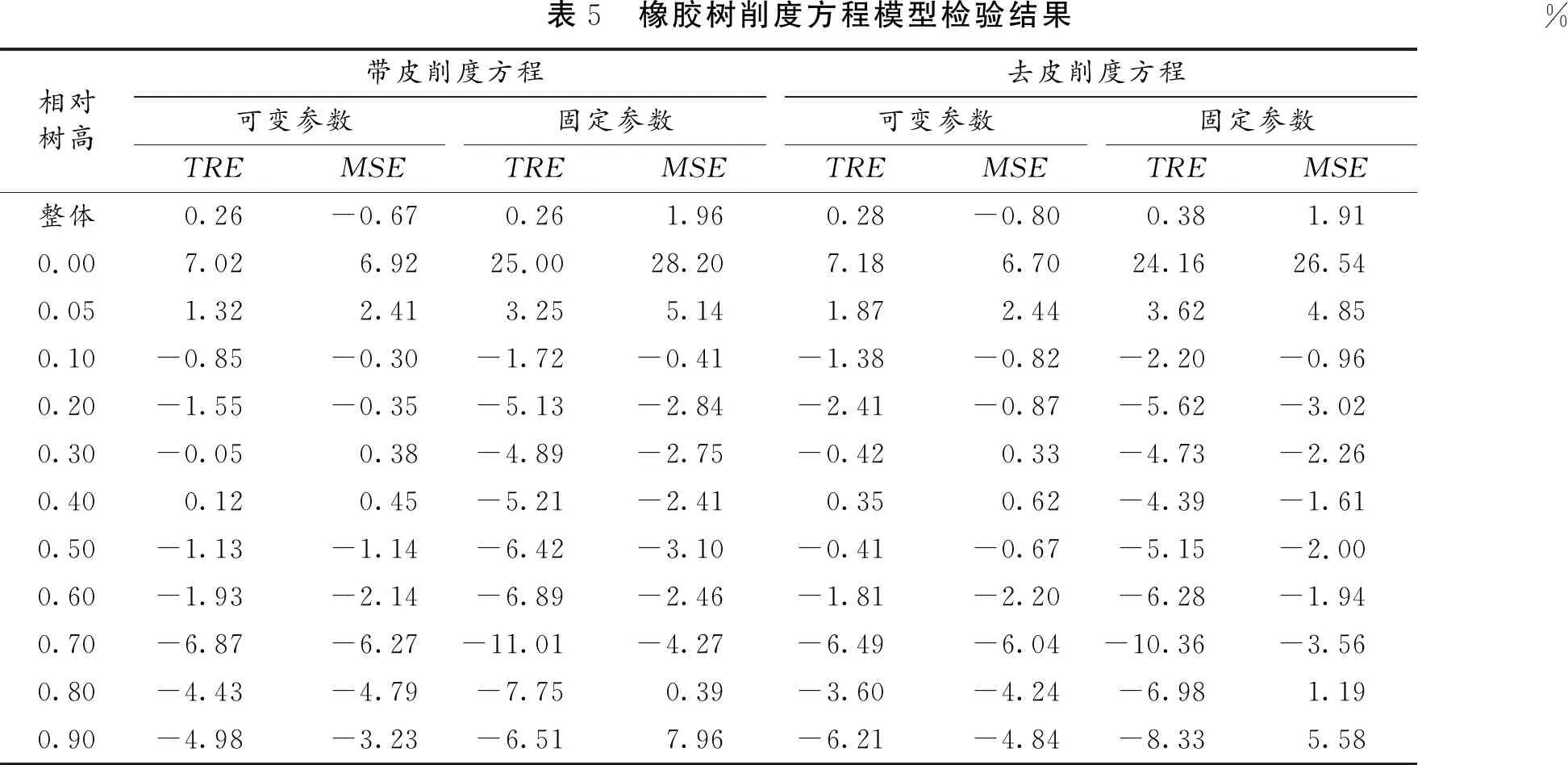
表5 橡胶树削度方程模型检验结果%相对树高带皮削度方程去皮削度方程可变参数固定参数可变参数固定参数TREMSETREMSETREMSETREMSE整体0.26-0.670.261.960.28-0.800.381.910.007.026.9225.0028.207.186.7024.1626.540.051.322.413.255.141.872.443.624.850.10-0.85-0.30-1.72-0.41-1.38-0.82-2.20-0.960.20-1.55-0.35-5.13-2.84-2.41-0.87-5.62-3.020.30-0.050.38-4.89-2.75-0.420.33-4.73-2.260.400.120.45-5.21-2.410.350.62-4.39-1.610.50-1.13-1.14-6.42-3.10-0.41-0.67-5.15-2.000.60-1.93-2.14-6.89-2.46-1.81-2.20-6.28-1.940.70-6.87-6.27-11.01-4.27-6.49-6.04-10.36-3.560.80-4.43-4.79-7.750.39-3.60-4.24-6.981.190.90-4.98-3.23-6.517.96-6.21-4.84-8.335.58

4 结论与建议

本文所建立的松树、橡胶树削度方程模型，经过模型检验分析后，充分表明：所建立的松树和橡胶树两个树种的削度方程预估精度高，达到了99%以上，模型均具有良好的全面切合性能，适用性能也良好，均可用于实际生产中；固定参数削度方程模型在树干两端存在着一定偏差，但就削度方程的应用来看，并不影响实际生产；可变参数削度方程模型要明显优于固定参数削度方程模型，是实际生产的首先。