复合材料薄层建模技术及电磁屏蔽效能评估

汪 昕，冯博文，闫丽萍，赵 翔

(四川大学 电子信息学院，四川 成都 610065)

0 引言

由于复合材料比重小、强度高等优点，已逐步取代金属合金，被广泛应用于航空航天、汽车、电子电气和建筑等领域。因此，对含复合材料系统或设施的屏蔽效能进行快速、准确评估具有重要意义[1]。复合材料作为电子设备壳体时，厚度一般为毫米级，远远小于波长和目标体的尺寸。采用传统时域有限差分(FDTD)算法进行计算时，为确保建模的准确性，计算区域需要采用精细网格剖分，需要消耗巨大的计算资源与计算时间。

为解决薄层结构的快速建模问题，嵌入式薄层建模技术[2-3]得到大量研究，该技术将薄层嵌入到相邻的粗网格之间，避免了整个计算区域网格剖分过密而带来的巨大计算成本问题。目前用于FDTD的嵌入式薄层建模技术主要有表面阻抗边界条件(SIBC)法[4-5]、阻抗网络边界条件(INBC)法[6-7]、有效边界条件(EBC)法[8]、传输线等效(TLE)法[9]以及亚网格边界条件(SGBC)法[10]。SIBC、INBC和EBC算法均通过薄层结构2个表面上电场和磁场的阻抗关系对薄层进行建模，这就要求电场和磁场需在空间和时间上同步，而FDTD计算中电场和磁场空间上相差半个网格，时间上相差半个时间步，因此必须进行场值外推，从而导致算法后期不稳定[11-13]。SGBC算法对薄层内部进行一维亚网格剖分，使用无条件稳定的一维隐式Crank-Nicolson TD (CNTD)方法[14]求解薄层内各节点上的场，避免了时间步长的减小；而薄层外的计算区域则采用常规三维FDTD方法进行更新。通过显隐式混合(HIE)算法将薄层内部亚网格和周围Yee氏粗网格连接起来，避免了外推计算，从而有效解决了后期稳定性问题。

本文采用SGBC算法结合FDTD算法，对复合材料薄层进行快速建模，计算了3种不同含复合材料薄层腔体在0.1～1 GHz频段内的电磁屏蔽效能，并与商业仿真软件CST计算结果进行对比。

1 亚网格边界条件法基本原理

SGBC法能够克服其他薄层建模技术普遍存在的后期不稳定问题，且易于实现，因而适用于含复合材料薄层结构的FDTD快速计算问题。当电磁波以任意角度入射到复合材料薄层结构的表面时，其折射波总是沿薄层表面的法线方向传播[10]，因此电磁波在薄层内部传播时可看作一维问题，薄层以外的区域则采用常规三维FDTD进行计算。这样避免在整个计算区域采用精细网格，极大地减少了计算资源，提高了计算效率。SGBC法的计算模型如图1(a)所示，薄层内的网格剖分如图1(b)所示。

图1 SGBC法薄层结构建模示意Fig.1 Schematic diagram of thin layer structure modeling with SGBC

以XOZ面的薄层为例，将复合材料薄层划分为N个亚网格，薄层内包含N+1个切向电场分量Ez，N个磁场分量Hy。薄层两端的电场分别用Ez，s1(Ez，1)和Ez，s2(Ez，N+1)表示，薄层内部第一个磁场分量为Hy，3/2，最后一个磁场分量为Hy，N+1/2，Hy，1/2和Hy，N+3/2为薄层相邻三维网格中心点的磁场分量Hy，s1和Hy，s2。

根据全电流定律和法拉第电磁感应定律，可以推导获得薄层内部电场分量Ez，i与磁场分量Hy，i+1/2的更新公式为：

(1)

(2)

式中，各系数分别为：

(3)

(4)

Da，n+1/2=1，

(5)

(6)

式中，εr表示薄层等效介电常数；μr表示薄层等效磁导率；σn表示薄层电导率。

将式(2)中的Hn+1带入式(1)，可获得薄层内部各节点上电场分量的三对角矩阵方程：

(7)

(8)

(9)

bi=1-ai-ci，

(10)

(11)

通过求解该矩阵方程，可获得薄层内所有网格的电场分量Ez，i，再代入式 (2)，即可得到薄层内所有磁场分量。

复合材料薄层中的场与外部Yee氏粗网格中的场通过边界条件连接到一起，构成SGBC-FDTD算法。例如复合材料薄层表面的电场Ez，1的计算用到相邻粗网格磁场分量Hy，s1；而粗网格中磁场分量Hy，s1的计算则需要Ez，1。

(12)

(13)

式中，ΔS为积分区域所围面积。

2 SGBC-FDTD算法在含复合材料薄层结 构腔体SE评估中的应用

首先计算了六面均为复合材料的封闭腔体中心点的电磁屏蔽效能，计算模型如图2(a)所示。复合材料的电导率为1 000 S/m[15]。垂直极化平面波沿-x方向垂直入射到腔体前面板上。计算得到0.1～1 GHz频段内腔体中心点的SE，如图2(b)所示。为了定量评估SGBC-FDTD算法与仿真软件结果之间的绝对差值和曲线变化趋势，采用文献[16]中的平均绝对误差MAV和曲线相关系数ρ作为评价指标。从图2(b)可以看出，SGBC-FDTD算法计算结果与CST计算结果吻合较好，二者平均绝对差值MAV= 1.422 dB，曲线相关系数ρ= 0.989。在0.714 GHz处出现谐振，与谐振腔理论结果相吻合。图2(c)给出了腔体中心点SE随复合材料厚度t的变化。可以看出，随着薄层厚度的增加，SE逐渐增大，且SE增加量随频率升高而增加，在1 GHz时提高近40 dB。这是由于复合材料的趋肤深度随频率增加而减小导致的。

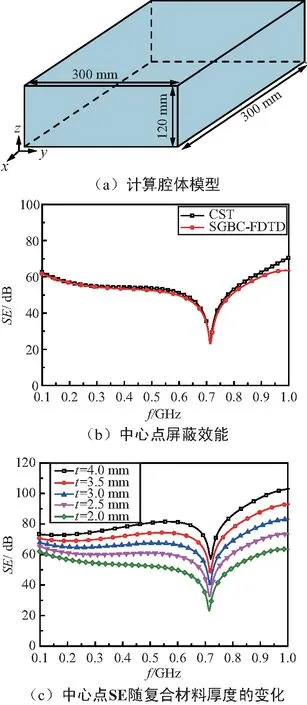
图2 复合材料封闭腔计算模型及屏蔽效能Fig.2 Calculation model and SE of the metallic enclosure made of composite material

只有一个面板为复合材料的计算模型如图3(a)所示，其中复合材料电导率为100 S/m，其余五面均为理想导体。垂直极化的平面波沿+x方向垂直入射到复合材料面板，计算得到腔体中心点的SE如图3(b)所示。由图中结果可以看出，SGBC-FDTD算法与CST计算结果相吻合，且频段内的平均绝对差值MAV= 1.466 dB，曲线相关系数ρ=0.984。与图2(b)结果相比，尽管该腔体只有一个面为复合材料，但由于其电导率过低，导致其SE低于电导率为1 000 S/m的六面均为复合材料腔体的SE。

图3 单面板为复合材料的封闭腔计算模型及屏蔽效能Fig.3 Calculation model and SE of the metallic enclosurewith single panel made of composite material

单面为复合材料的封闭腔计算模型及斜入射时的屏蔽效能如图4所示。

图4 单面为复合材料的封闭腔计算模型及斜入射时的屏蔽效能Fig.4 Calculation model and SE for oblique incidence of the metallic enclosure with single panel made of composite panel

图4(a)给出了电磁波斜入射到单面为复合材料腔体的计算模型，其电导率仍为100 S/m。垂直极化平面波的入射方向为θ= 90°，φ= -45°。腔体中心点SE在0.1～1 GHz频段内的计算结果如图4(b)所示。与CST计算结果相比，二者平均绝对差值MAV=1.385 dB，曲线相关系数ρ=0.980 1。图4(c)为垂直入射和斜入射时屏蔽效能结果的对比。根据电磁场理论知识得知，电磁波斜入射时的透过复合材料进入腔内的能量少于垂直入射的情况，因此斜入射时腔体中心点的SE值高于垂直入射时的SE值。

SGBC-FDTD算法用于含复合材料薄层结构腔体的SE评估时，不仅计算结果与仿真软件相吻合，而且计算资源占用大幅减少，计算效率提升显著。例如对于上述第一个算例，在同一台工作站上SGBC-FDTD算法中网格总数约为CST的0.3%，计算时间约为CST耗时的7.4%。

3 结束语

采用SGBC-FDTD算法实现了含复合材料薄层结构腔体的电磁屏蔽效能计算，3种不同情况下腔体在0.1～1 GHz的频段内的屏蔽效能结果与商用软件CST的计算结果相吻合。通过二者计算时间、计算成本的对比验证了SGBC-FDTD算法的高效性，为实际应用中对含复合材料薄层结构腔体的电磁屏蔽效能计算提供了参考。同时，可尝试对算法进行进一步改进，实现对色散、有耗媒质薄层的高效建模。