盾构同步注浆浆液压力影响因素及扩散机理
胡长明,郭建霞,梅 源,王志宇,袁一力
(1.西安建筑科技大学 土木工程学院,陕西 西安 710055;2.西安建筑科技大学 陕西省岩土与地下空间工程重点实验室,陕西 西安 710055)
当前盾构施工技术以其独特的优势在隧道施工过程中占据着重要地位,但盾构施工不可避免地会对周围环境造成扰动和影响,如地面沉降,临近建筑物倾斜、沉降,地下管线破裂等.在盾构施工过程中,盾尾同步注浆是控制地层变形的关键施工工艺[1],而注浆压力是决定浆液在管片壁后充填扩散及压力分布的重要参数,其大小直接影响着既有建筑物和地层的沉降.另外盾尾同步注浆浆液压力的分布形式对地层变形和管片结构受力变形具有决定作用[2-3].研究盾构施工同步注浆浆液填充及扩散机理对控制地面沉降、管片变形及位移等具有重要意义.
关于盾尾注浆浆液扩散及压力分布问题,学者们分别从数值模拟[3]、现场试验[4]、模型试验[5]及理论分析[6-13]角度进行了研究.其中基于理论分析建立的浆液扩散模式包括半球面扩散[8]、柱面扩散[9]、扇形扩散[7]、沿隧道横断面环形流动扩散[10-13]等,半球面扩散和柱面扩散是针对管片注浆孔注浆建立的浆液扩散模式,扇形扩散和环形流动扩散是针对同步注浆工艺提出的浆液扩散模式.目前针对同步注浆浆液的扩散模式以环形流动扩散研究较多,然而在对浆液扩散问题进行力学分析时,其中一些研究将管片环外壁和周围地层对浆液的流动阻碍作为作用于浆液的沿程阻力[7,10-12],另一些研究将盾尾横断面、已注入浆液对浆液的流动阻碍作为作用于浆液的沿程阻力[13].由此可以看出以上研究工作都只考虑浆液在过流断面上一个方向的流速变化情况(即将浆液流动假设为一元流动),未能全面揭示浆液在全流动断面上的流变特性,而且考虑流体不同方向流变特性所得计算结果也不相同.此外,在分析流体在矩形截面流道的流动规律时,若长宽比小于10,应当将流体流动视为二元流动,考虑双向沿程阻力的作用[14].
基于以上分析,本文在论述了盾尾同步注浆浆液环向填充过程的基础上,分析了影响浆液压力扩散的相关因素,并在考虑浆液流动时受双向沿程阻力作用的基础上,建立了浆液在盾尾空间中二元流环形扩散空间力学模型,最后基于牛顿流体和宾汉姆流体的流变特性分别推导了浆液压力分布理论计算式,为盾构同步注浆浆液压力分析提供新的理论依据.
1 浆液填充过程及扩散影响因素
1.1 浆液在盾尾间隙的环向填充及压力扩散
在盾构掘进过程中,浆液在注入盾尾间隙后沿着一定路径进行充填,其运动规律取决于自身的流变特性与盾尾间隙的几何模型[10].在实际工程中,由于盾构机在单位时间内的掘进长度远小于隧道结构的空间尺度,因此可将盾构掘进单位时间内所形成的盾尾间隙看作一个厚度较小的环状空间,浆液由注浆孔注入空间后,沿环形空间横断面形成流动截面,然后沿着环状空间环向进行充填,该填充过程也是浆液压力的扩散过程.由于浆液实际填充过程比较复杂,因此在理论分析时,文献中一般将浆液压力的扩散和消散分为两个相对独立的过程,浆液压力的扩散过程主要沿隧道盾尾间隙横断面(隧道环向方向),消散过程主要沿隧道盾尾间隙纵断面(隧道轴向方向).本文主要研究浆液压力沿盾尾横断面的扩散问题,图1为浆液的流动填充过程示意图.

图1 浆液环向填充过程Fig.1 Slurry circumferential filling process
图中设盾尾间隙为b,所形成的环状空间沿隧道轴向的宽度为δ,衬砌外径为R.
1.2 影响因素
同步注浆浆液从注浆孔注入环状空间后,沿环向向远处充填扩散,若注浆压力不变,驱动浆液运动的压力由于受到浆液自身的黏性作用、沿程摩阻力和其他外力(如重力)的综合影响,浆液的整个运动扩散过程变得非常复杂.然而从浆液注入盾尾空隙到扩散至最远处的整个过程不难看出,浆液压力的扩散与盾尾空隙的周围土质、地下水、浆液性质、注浆工艺、盾构施工工艺等因素有很大关系[11],在不同的地质环境下,影响浆液压力分布的因素也不尽相同.本文以硬岩或稳定性地质条件下的浆液扩散过程为研究对象,在该地质环境下,总结影响浆液扩散的因素主要包含如下几个方面:(1) 浆液自身特性,如浆液密度、黏度系数和初始剪切力(非牛顿流体);(2) 注浆工艺参数,如注浆压力、注浆量(或注入率)、注浆孔数量和位置等;(3) 盾构掘进参数,如掘进速度、隧道直径和盾尾间隙等.由于浆液的扩散和压力分布受到上述各因素的混合影响和限制,因此有必要对浆液在盾尾空隙中的运动扩散过程作简化.
2 基本简化及假设
为建立浆液在盾尾空间中的二元流扩散模型,对浆液在盾尾空间中的填充路径做适当简化,如图1中所示,当浆液由注浆孔注入空隙后,将其沿管片环流动的弯曲路段分解为很多微小的直线段[10],同时做出如下基本假设:
(1)浆液为不可压缩的均质、各向同性流体,由于浆液在所研究填充空间内的填充时间比较短,且以水泥基浆液为主要研究对象,故不考虑浆液黏度随时间的变化.
(2)浆液流动状态近似为层流.
(3)浆液在填充过程中,不考虑浆体与管片、盾体、土体在接触面上的相互渗透作用.
(4) 浆液在注入盾尾空间后沿隧道轴向和径向形成流动截面,然后沿管片的外环面环向流动填充空间,其流动的沿程速度损失不计.
(5) 盾构掘进过程中形成的盾尾间隙沿管片环向均匀分布.
3 理论分析
基于前述分析,建立以管片环圆心为坐标原点的直角坐标系,取水平方向为x轴,竖直方向为y轴,隧道轴向方向为z轴.取环形空隙中任一点流体微元进行受力平衡分析如图2,由于浆液沿管片环向上和向下流动时受力模式不同,需分别进行讨论,图2为浆液向下流动时的受力分析.
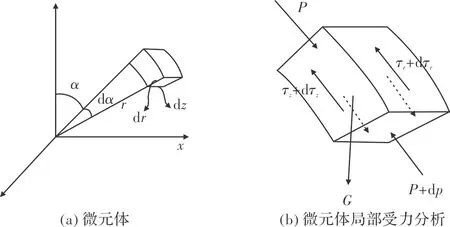
图2 浆液向下流动受力分析Fig.2 Mechanical analysis of downward flow of grouting
根据极限受力平衡分析,可得
(1)
其中:p为微元体浆液压力函数,α为微元体与y轴的夹角,r为微元体距坐标原点的径向长度,dr、dz分别为微元体沿管片径向和轴向的长度,dα为微元体沿管片环向的弧度,ρ为浆液密度,τr、τz分别为剪切应力函数.

(2)
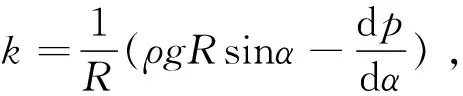
(3)
由式(3)可以看出,k值是计算浆液压力的关键因子,该值主要取决于流体两个方向的剪切应力,但对于不同流变模型的流体,需要对k值分别进行讨论.在理论研究中常将同步注浆浆液视为牛顿流体或宾汉姆流体[16],以下针对这两种流体分别进行推导.
3.1 牛顿流体
浆液流动特性符合牛顿流体模型时的流变模型为
τ=-μγ
(4)
其中:τ为应力张量,μ为流体动力黏度系数,γ为剪切变形速率张量.
本研究中τ的表示形式为
(5)

将(5)式代入(3)式可得
(6)
该微分方程的边界条件为
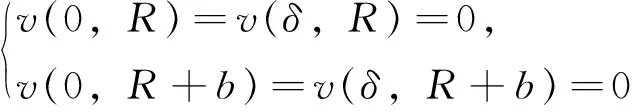
(7)
求解 (6) 式,并代入(7)式的边界条件,可得流体的流速为
(8)
对(8)式在区域z∈[0,δ],r∈[R,R+b]进行积分可得过流断面的单位流量为
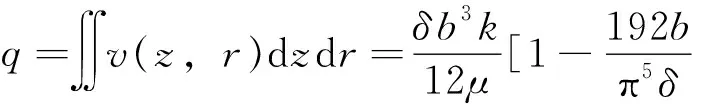
(9)

k=12μq/δb3M
(10)
式(10)即为牛顿流体的k值计算式.
3.2 宾汉姆流体
浆液符合宾汉姆流体时的流变模型[15]为
(11)
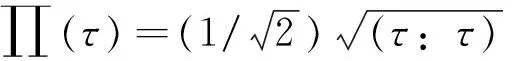
本研究中τ、∏(τ)、∏(γ)的表示形式为
(12.1)
(12.2)
(12.3)

从(12.1)~(12.3)式可以看出,基于宾汉姆流体的浆液压力分析问题是非线性问题,因此本文在分析宾汉姆流体的浆液扩散问题时通过适当的简化假设,以数值计算为主,本节主要介绍其求解方法和步骤.
(1)转换坐标,如图3所示,以盾尾间隙断面中心为坐标原点o′,隧道径向为r′轴,轴向为z′轴,则其边界条件可表示为
(13)

图3 坐标转换Fig.3 Coordinate transformation

(14)
参数η在求解过程中根据相关条件获得,详见步骤(3).
(3) 将步骤(2)中线性化处理条件代入(3)式,可得
(15)
根据(15)式计算可得流体在坐标轴r′和z′上的剪切应力表达式.

(16)
将坐标轴r′和z′上剪切应力表达式代入(14)式,并求解,可得流体在坐标轴上的流速分布
(17)
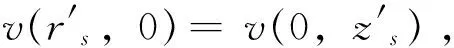
(4)根据步骤(2)中线性化处理条件,同时联立式(3)、(12.1)、(12.3)及(13)得到一个二阶微分方程,

(18)
求解该微分方程可得屈服面外的流体流速.
(5)在整个流动断面上对步骤(3)和步骤(4)中得到的流速进行积分即为单位时间内的浆液流量.已知浆液流量为q,从而可通过数值计算得到宾汉姆流体的k值.
3.3 浆液压力

dp=(ρgRsinα-Rk)dα
(19)
根据边界条件α=αi,p=pi(pi为第i个注浆孔的注入压力,注浆孔处的注浆压力为已知参数,可根据工程实际或经验确定,αi为第i个注浆孔的位置角度)并对(19)式在区间α∈[αi,α],p∈[pi,p]进行积分,可得浆液沿环面向下流动的压力计算式为
p=pi+ρgR(cosαi-cosα)+Rk(αi-α)
(20)
同理可推得浆液沿环面向上流动的压力计算公式为
p=pi+ρgR(cosαi-cosα)-Rk(αi-α)
(21)
由式(20)和(21)可知,决定浆液压力分布的主要因素是注浆压力、浆液自重(式中第二项)及浆液剪切作用(式中第三项).如1.2节中所述,上述推导过程以硬岩或稳定性地层为基本前提条件,因此所得的压力计算公式可适用于泥岩,黄土等成形效果较好的土质环境.
4 工程算例验证及分析
根据文献[4]中对Sophia工程隧道监测数据和工况参数,对本文中推导的盾尾同步注浆浆液扩散模型进行验证分析.相关参数见表1和表2.

表1 注浆孔点位及注浆压力Tab.1 Grouting position and grouting pressure of tunnel

表2 盾构掘进参数及浆液特性参数[4]Tab.2 The parameters of shield and slurry property [4]
4.1 浆液压力计算
设每个注浆孔单位时间内向上向下流量相等,且按注入总流量平均分配,工程中的注浆浆液总流量由所填充的盾尾间隙空间体积和浆液注入率决定,此处设浆液注入率m为150%,则单位时间各个流动断面的流量为
4.347×10-4m3/s
根据文献[7]中研究结果暂取盾构机推进30 s时的长度作为隧道轴向方向上的理论研究尺度,即δ=v盾t=0.021 6 m
将表1与表2中参数及qi、δ代入上文第3节中的牛顿流体和宾汉姆流体浆液压力计算模型,可得相应流体模型的浆液扩散初期压力分布情况如表3和图4所示.
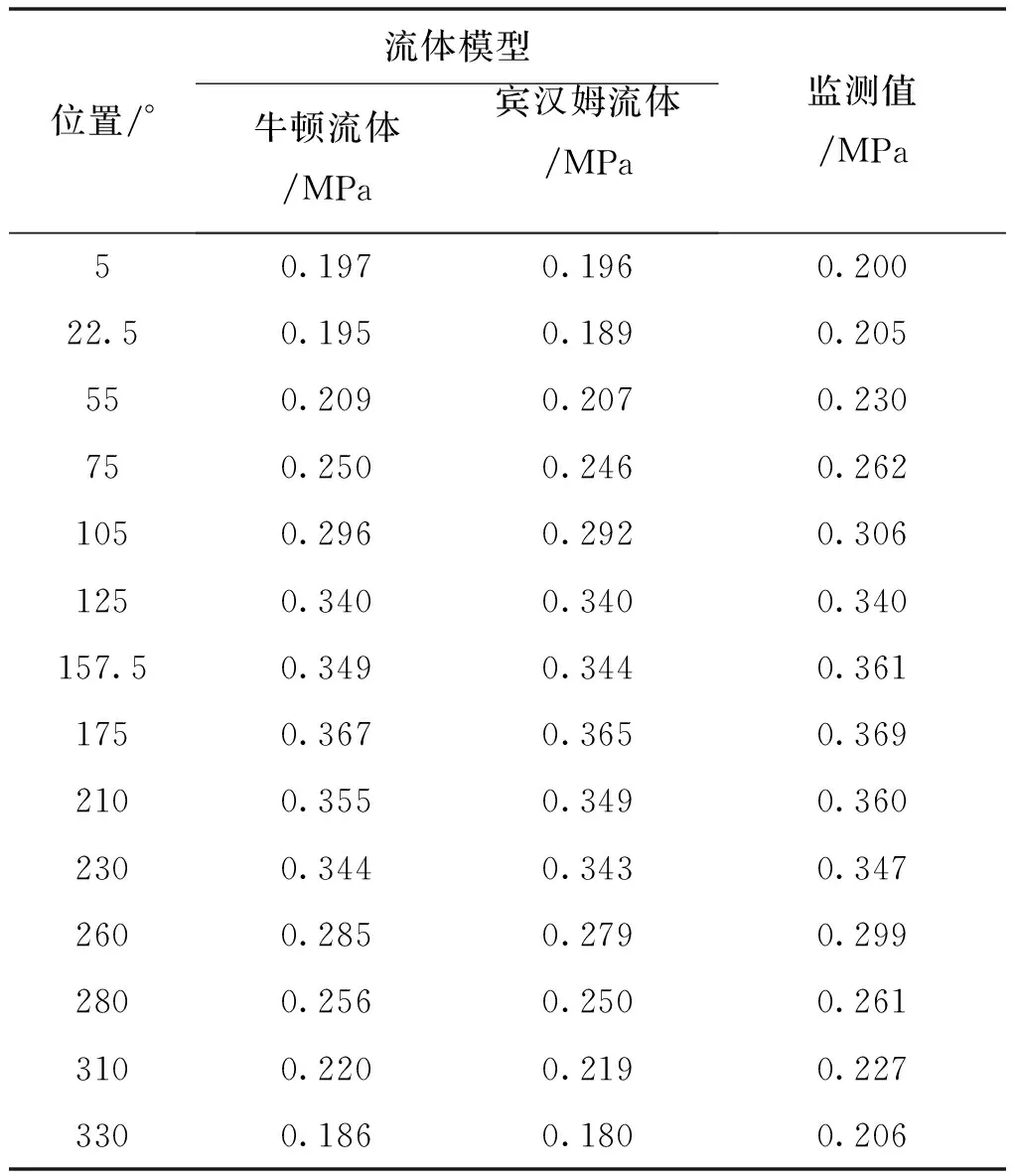
表3 浆液压力监测值及其对应的计算值
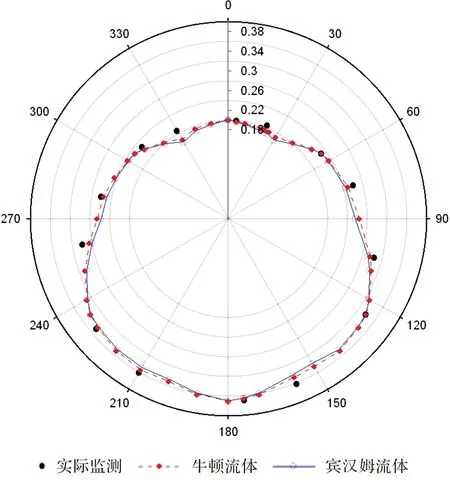
图4 计算值与监测值对比(单位:MPa)Fig.4 Comparison between calculated and measured values (unit: MPa)
由图表中可以看出,浆液二元流扩散理论模型计算值与实测值吻合较好,在流体各参数相同的情况下,两种流体模型计算结果差别较小.但由于宾汉姆流体需要克服初始动切力作用,其计算结果总体小于牛顿流体的计算结果.在实际中,由于不同水泥浆液的水灰比、密度等参数不同,所呈现的流变特性也不同[16],在实际应用时需根据浆液的具体特性选取相对应的计算模型.
通过对已有研究的一元流环形扩散模型计算结果对比可得,假设流体速度沿z(隧道轴向) 方向变化,其结果比假设沿r(隧道径向)方向变化有一定程度的减少,对于牛顿流体和宾汉姆流体,其对比结果如表4所示,表中为不同模型的相对压差均值结果对比.

表4 不同模型计算结果对比Tab.4 Comparison of different models
从表中可以看出,两种一元流扩散模型不能得到统一的计算结果,本文推导的浆液二元流环向流动扩散模型能够弥补已有研究模型的不足.对于牛顿流体,本文所得浆液压力计算结果较已有研究模型(流速分别沿r、z方向变化)的计算结果平均减小3.11%和0.30%;对于宾汉姆流体,计算结果平均减小1.51%和0.68%.但由于本文采用了更精确的模型假设,因此理论分析结果更接近真实情况.
4.2 浆液流速分布
4.2.1 牛顿流体流速分布
图5为浆液符合牛顿流体模型时的断面流速分布(图(a))和r=4.805 m,z=0.010 8 m(流动断面对称轴)处流速分布(图(b)、(c)).
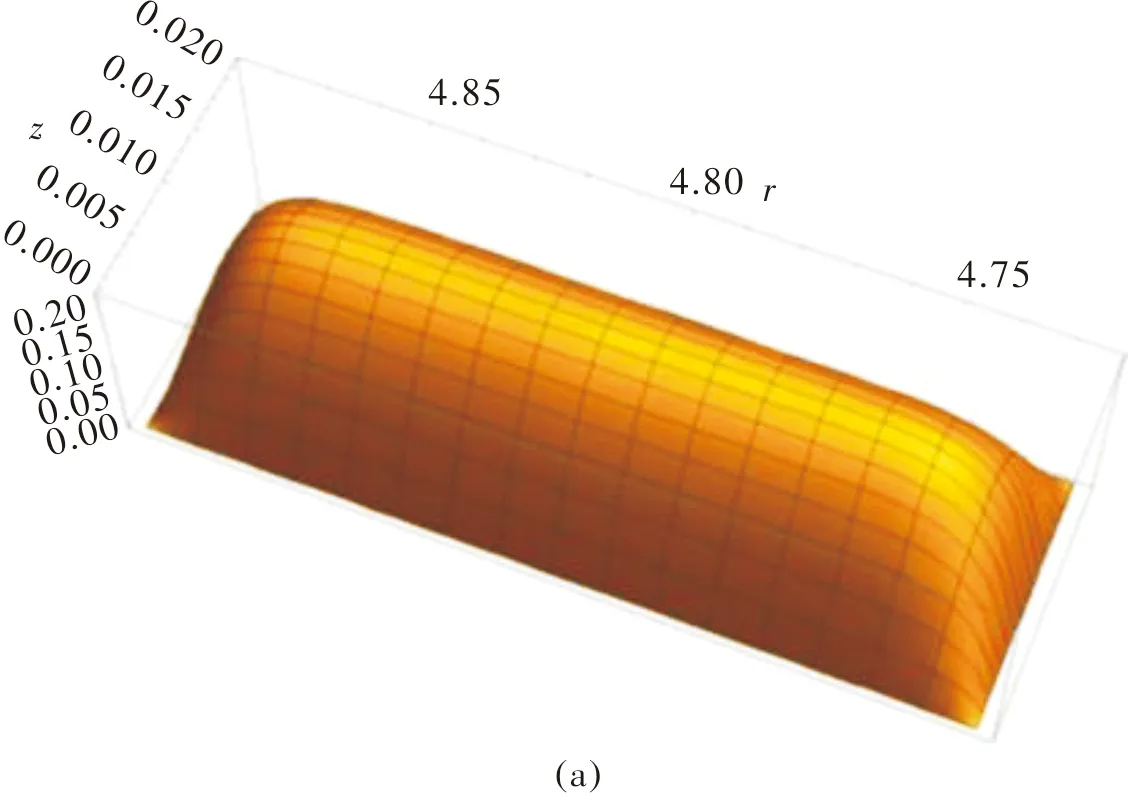

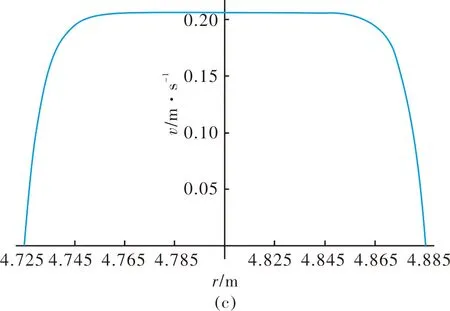
图5 牛顿流体模型流速分布Fig.5 The velocity distribution of Newtonian fluid
图中显示,由于考虑流体受双向摩阻力作用,浆液在流动断面的中心位置流速最大,从中心向两个方向流速逐渐减小.在r=4.805 m处,流速成抛物线型变化,这与已有一元流模型研究结果相似;在z=0.0108 m处,流速在约[4.755,4.855]范围内呈现平台状微小变化,在[4.725,4.755]和[4.855,4.885]范围变化幅度比较大,而已有模型未能揭示该方向的流速变化情况.该结果与文献[17]中使用激光自混合测量结果相吻合,从而可验证本文理论分析结果的可靠性.
4.2.2 宾汉姆流体流速分布
图6为浆液符合宾汉姆流体模型时的流速分布(图(a))和坐标轴r′=0,z′=0(流动断面对称轴)上流速分布(图(b)、(c)).
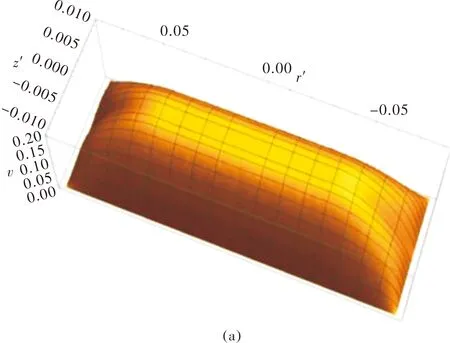


图6 宾汉姆流体模型流速分布Fig.6 The velocity distribution of Bingham fluid
图中显示,宾汉姆流体流动时存在活塞区和屈服区,在活塞区速度相同,流体呈活塞式整体流动,这与已有模型研究结果相似;但在r′=0处,活塞区分布范围较小,在z′=0处,活塞区分布范围较大.在屈服区,类似牛顿流体特性,流速从屈服面向两个方向边界处逐渐减小.而已有的一元流环向流动模型并不能得到上述流速变化情况.
上述分析内容可直观揭示浆液二元流扩散模型在整个过流断面上的流变特性,可为同步注浆浆液环向扩散理论研究提供新的视角.
4.3 影响因素分析
由理论推导结果可知,影响浆液压力的因子主要为注浆压力、浆液自重及浆液剪切力.其中浆液自重主要取决于密度ρ,浆液剪切作用主要取决于参数k的取值.另外由于浆液填充时间t决定着模型中盾尾环空间沿隧道轴向的宽度δ和参数k的取值,研究其对浆液压力分布的影响也具有重要作用.因此本节假设其它参数不变,主要研究浆液密度、参数k及浆液填充时间对浆液压力分布的影响规律.由于实例中浆液属于宾汉姆流体,以下分析仅考虑浆液为宾汉姆流体的情况.
4.3.1 浆液密度
分别计算拱顶10°、拱腰100°和拱底190°处浆液压力随浆液密度的变化值,如图7所示.

图7 浆液压力与密度的变化关系Fig.7 The relation between slurry pressure and density
随着浆液密度的增加,拱顶10°处浆液压力逐渐增大,拱腰100°和拱底190°处浆液压力逐渐减小.结合前述理论计算式可知,由于在10°位置处浆液向下流动,重力做正功,因此浆液压力会随着浆液密度的增大而增加;而在100°和190°位置处浆液向上流动,重力做负功,浆液压力随密度的增大而不断减小.
由于10°和190°位置处距离注浆孔较近,密度变化引起的重力功变化较小,浆液压力变化幅度较小;在远离注浆孔位置处(拱腰100°处),密度变化引起的重力功变化较大,浆液压力急剧变化.由此可知,浆液密度对管片环向尤其远离注浆孔位置处的浆液压力具有决定作用.
4.3.2 浆液剪切力
分别计算不同k值时拱顶10°、拱腰100°和拱底190°处的浆液压力,如图8所示.

图8 浆液压力与k值的变化关系Fig.8 The relation between slurry pressure and k
图中显示,当k值由100增大至12 150时,三个位置处的浆液压力均不断越小.结合前述理论计算式可知,不论浆液向上还是向下流动,剪切力均做负功,因此随着k值的增加,浆液压力均不断减小.但在近注浆孔位置(10°和190°)处,浆液压力随k值的变化幅度较小,在远离注浆孔位置(100°)处,浆液压力随k值的变化发生剧烈变化.由此可知,k值(剪切力)对浆液压力(尤其在远离注浆孔位置处)的变化有着重要影响.
4.3.3 浆液填充时间
相关研究结果显示[7],浆液沿着管片环向流至两注浆孔中间位置所需最短时间为30 s,完全充满盾尾空间需要100 s以上.取填充时间10 s至110 s 变化时的浆液压力进行分析,结果如图9所示.
由图可知,在盾构推进速度一定时,浆液填充时间越长,拱顶、拱腰和拱底处的浆液压力越大,并当t≥30 s时逐渐趋于一个定值.说明浆液压力随着填充时间的增加逐渐稳定,当填充时间接近100 s以上时,浆液压力也达到盾尾间隙完全充满状态的压力值.由此可知在运用本文的浆液二元流扩散理论模型分析浆液压力时,应取浆液填充时间最少为30 s.

图9 浆液压力与填充时间的变化关系Fig.9 The relation between the slurry pressure and filling time
5 结论
本研究在分析浆液环向填充扩散过程的基础上,基于简化假设条件建立了盾构同步注浆浆液的二元流环形扩散模型,改进了已有模型的不足,并通过工程实例进行验证分析,得出如下结论:
(1)本文的浆液二元流环形扩散模型的压力计算值与实测结果吻合度较好,由于考虑了浆液流动受双向摩阻力作用的环形扩散模型更接近于工程真实情况,其分析结果能够为工程实践提供更可靠的理论依据.
(2)分析浆液的二元流环形扩散模型在流动断面上的流速分布可得,浆液为牛顿流体时的流速在流动断面中心位置最大,从中心向两个方向的边界逐渐减小为零.浆液为宾汉姆流体时,在断面中间位置的活塞区流速相同,从活塞区(屈服面)边界向两个方向流速呈抛物线减小.该分析结果可全面揭示流体在流动断面上的流速分布情况.
(3) 浆液自重和浆液剪切力对浆液初始压力分布(尤其在远离注浆孔位置处)具有决定性作用.浆液填充时间对浆液压力的计算结果有重要影响,在分析浆液压力时,应根据具体情况取填充时间大于30 s.

