成层地基中考虑桩桩相互作用的双排桩受力变形分析
张玲,欧强,朱幸仁
(湖南大学 岩土工程研究所,湖南 长沙 410082)
近十多年来,由前排桩、后排桩和连系梁(板)组成的双排桩支护结构,因其具有较大的侧向刚度,可有效限制支护结构变形且不需设置内支撑,相较于拉锚结构又无需太多场地,而在基坑支护工程中得到广泛应用[1-8].但双排桩支护结构受力变形机理及设计计算非常复杂,为此国内外不少学者对此展开了深入研究.余志成等[9]首先在深基坑挡土护坡桩中采用双排桩支护形式,并通过模型试验验证了双排桩的整体刚度大和水平位移小的特点.OU 等[10]进行了基坑开挖的数值模拟分析,研究了基坑开挖过程对双排桩支护结构的作用效应.何颐华等[1]基于土拱理论提出一种双排桩支护结构的土体积比例系数法,认为前、后排桩所受侧向土压力是按前、后排桩之间滑动土体占土体总量的比例关系确定的.刘钊[11]提出了桩土相互作用的3 种情况,分为基坑底面以上部分桩后土、桩间土以及基坑底面以下的土.黄强[12]基于朗肯土压力理论,首次提出刚塑性分析法,通过独立的刚塑性体分析桩间土体,并提出了空间效应系数.曹净等[13]通过引入等效桁架模型,将前、后排桩桩间土等效为平面桁架结构,进而提出一种基坑双排桩支护结构的改进计算模型.张玲等[14]考虑桩桩相互作用对双排桩进行了受力变形分析.彭文祥等[8]、张虎元等[15]、郑轩等[16]对双排桩结构最佳排距和破坏形式进行了模型试验研究.
以上研究大都是基于均质地基中的双排桩支护结构进行分析,但实际的土层大多是成层的,因此有必要对成层地基中的双排桩支护结构开展研究.高阳等[17]采用有限差分数值方法,考虑了桩土相互作用对双排桩进行了三维动态分析.顾问天等[18]基于比例系数法和排桩反力弹簧原理提出了反力弹簧法,不同土层选用不同刚度的弹簧进行模拟,可准确描述土的变形情况和土体分层情况.杨德建等[19]和尹建峰等[20]得到了相似的规律.上述研究[18-20]表明,考虑地基土的成层性对描述双排桩支护结构的受力和变形更加符合实际情况,但忽略了桩-桩相互作用.实际工程中,当后排桩桩后作用水平推力时,后排桩向坑内发生挠曲变形并挤压桩间土体;受挤压的桩间土体传递水平荷载,又对前排桩产生水平推力作用,使其也向坑内发生挠曲变形,进而挤压前排桩桩前土体.但通常桩间土具有一定程度水平向的压缩变形,前、后排桩挠曲变形不一致.蔡袁强等[21]指出双排桩间距过小时,支护结构特性与悬臂式单排桩性能相似.当排距过大时,其特性与拉锚桩相似;当排距等于4 倍桩径时,支护结构才能发挥最大的性能.郑刚等[22]提出了一种考虑部分桩土相互作用的平面杆系有限元双排桩分析模型,将双排桩之间土视为薄压缩层,并以水平向弹簧模拟.因此对成层地基中的双排桩支护结构进行分析研究时,应充分考虑桩桩以及桩土的相互作用.
鉴于此,本文在郑刚等人[22]研究的基础上,基于Euler-Bernoulli 双层梁理论,充分考虑桩桩相互作用、桩土相互作用、地基土成层性以及地基反力系数的线性变化等因素的影响,对双排支护桩的受力变形进行分析,以期为双排桩支护结构的设计计算提供参考.
1 计算模型的建立
1.1 双排桩计算模型
根据文献[22]的平面杆系有限元模型,建立如图1 所示计算模型.图中前、后排桩等长,桩身总长度为L,排距为D,基坑开挖深度为h,以基坑开挖面为界,开挖面以上n1层土,开挖面以下n2层,以土层分界面对桩身进行分段,共分为N 段,N=n1+n2.每层土中的桩段均有一个独立的“y-z”坐标系与其对应.参考文献[22],将成层地基中的前、后排桩与桩间土的相互作用以不同刚度的水平弹簧模拟.为便于计算,作如下假定:

图1 成层地基中双排桩支护结构计算模型Fig.1 Calculation model of double-row pile in layered foundation
1) 前、后排桩均视为竖向放置的Euler-Bernoulli 梁;
2)连系梁视为刚性体,即忽略其轴向的压缩或拉伸变形;
3)连系梁与前、后桩桩顶的连接为刚性连接.
1.2 受力分析
1.2.1 后排桩桩后土压力的计算
后排桩桩后土压力按朗肯主动土压力计算[23],且开挖面以下土压力视为矩形分布,如图1 所示.

式中:pi为第i 层土作用在后排桩上的主动土压力强度,kPa;F 为地面超载,kN;γi为第i 层土的天然重度,kN/m3;Hn为第n 层土的厚度,m;zi为第i 层土的厚度,m;ci为第i 层土的黏聚力,kPa;b 为桩间距,m;kai为第i 层土的朗肯主动土压力系数,1≤i≤N.
1.2.2 桩间土作用力的计算
前、后排桩在水平推力作用下发生挠曲变形,结合双排桩支护结构计算模型(图1),桩间土相互作用力可表示为式(2).

式中:q1,i为基坑第i 层土的桩土相互作用力,kN;b0为桩的计算宽度,m,按表1 选取[24];y1i为后排桩第i段桩身的挠曲变形,mm;y2i为前排桩第i 段桩身的挠曲变形,mm;k1,i为第i 层土的地基反力系数,当桩长大于桩排距的4 倍(即相当于大于桩间土厚度5倍)时,通常可将其理解为薄压缩层,因此可通过式(3)计算k1,i值[22].

式中:Esi为水平方向桩间土的压缩模量平均值,其值按工程地质手册确定.
当桩长小于桩排距的4 倍,且桩身入土深度范围内存在多层土时,考虑地基反力系数k1,i随深度呈线性变化,每层土的k1,i可按式(4)计算.


表1 桩的计算宽度Tab.1 Calculation width of pile
1.2.3 前排桩桩前土抗力的计算
前排桩桩前基坑底面以下土体抗力为:

式中:q2,i为前排桩土体抗力,kN;k2,i为第i 层土的地基反力系数,当1≤i ≤n1时,前排桩桩前为基坑开挖区,无地基反力作用,即:

当n1+1≤i≤N 时,考虑地基反力系数k2,i随深度的线性变化,

2 基本方程的建立与求解
2.1 基本方程的建立
根据上文对前、后排桩受力特点的分析,分别建立双排桩各微段的挠曲变形微分方程.
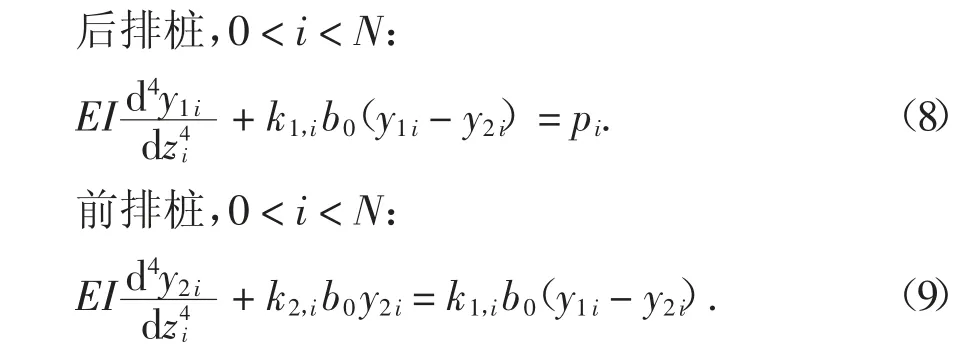
式中:EI 为桩身抗弯刚度.
2.2 基本方程的求解
将式(8)改写为:


根据第i 桩段与第i-1 桩段在土层分界面处的位移与内力的连续性条件,可得:

式中:y1(i-1),1(i-1),θ1(i-1),1(i-1),M1(i-1),1(i-1),Q1(i-1),1(i-1),y2(i-1),1(i-1),θ2(i-1),1(i-1),M2(i-1),1(i-1),Q2(i-1),1(i-1)分别为两个桩的i-1 桩段的底端位移、转角、弯矩和剪力.
根据传递矩阵法,结合式(19)(21),将第i 段到第1 段的内力位移连乘,即可获得i 段与第1 段的内力和位移的关系.
同理将式(13)求4 次和8 次导数并结合式(12)可得开挖面以下后排桩桩身挠曲变形方程的系数.后续计算同前一致,最后再结合桩顶和桩底的边界条件即可求解前、后排桩的桩身位移、转角、弯矩与剪力.对于桩底的约束条件可考虑以下几种情况:
1)桩底受铰接约束作用,即弯矩和位移为0;
2)桩底只受竖向约束作用,即弯矩和剪力为0;
3)桩底为自由端,即弯矩和剪力为0.
3 算例验证
采用本文方法对文献[22]的双排桩支护结构进行分析.工程情况简介如下:某酒店工程基坑地面以上17 层(局部19 层),地下1 层.基坑开挖深度为6 m,地下水位于1 m 左右,工程地质状况见表2.基坑支护结构采用双排钻孔灌注桩排列成梅花形状,桩顶设置冠梁,桩顶位于自然地面下2 m.基坑围护结构主要设计参数是:双排桩,桩径600 mm,桩长16.8 m,排间距2.5 m,桩间距1.5 m,m 值根据天津软土经验值取1 500 kN/m3,其他工程资料详见文献[22].
根据实际情况确定边界条件:前、后排桩桩底位移、弯矩为0;前、后排桩桩顶位移相等,前排桩桩顶转角为0.文献[22]考虑基坑开挖面以上后排桩土压力呈三角形分布,基坑开挖面以下为矩形分布,并且考虑桩间土与前、后排桩的相互作用进行了理论计算分析.将本文方法计算结果与文献[22]结果进行比较,比较结果如图2 和图3 所示.

表2 各土层物理力学参数指标Tab.2 Physical and mechanical parameters of each soil layer
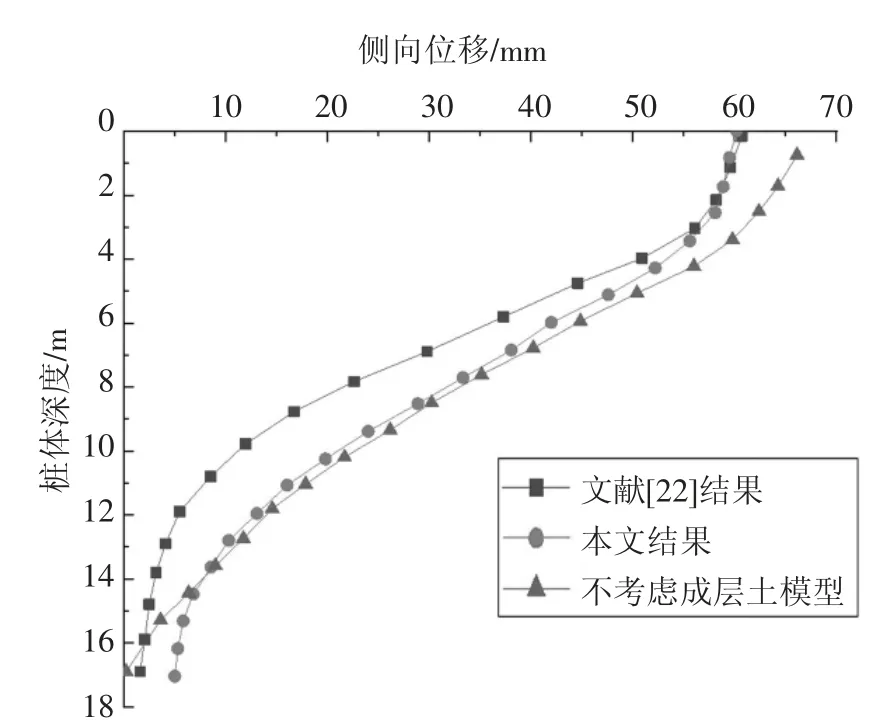
图2 前排桩侧向位移图Fig.2 Lateral displacement diagram of the front row piles
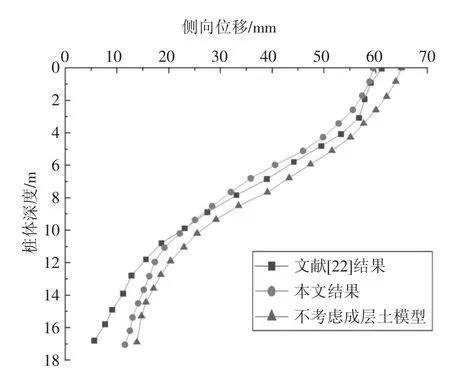
图3 后排桩侧向位移图Fig.3 Lateral displacement diagram of the rear row piles
由前、后排桩的侧向位移对比分析得知:本文前排桩的变形趋势与文献[22]结果基本一致,前排桩桩身侧移在桩身下半部分有一定增大的趋势,这主要是本文使用一系列非线性弹簧更加合理地考虑了桩土相互作用.后排桩的侧向位移在开挖面以上和文献[22]吻合较好,在开挖面以下有一定的差异,可能是由于本文假设后排桩基坑底面以下的主动土压力随土层线性变化,而文献[22]则假设基坑底面以下的土压力为矩形分布,在深度较大时,本文计算的土压力较文献[22]偏大,从而导致作用在双排桩上的横向荷载偏大,因此在后排桩的底部侧移较文献[22]偏大.本文土压力的分布假设更加符合建筑基坑支护技术规程[23]的要求.从整个双排桩支护结构来看,前、后排桩的侧向位移与文献[22]的变化趋势基本一致,验证了本文方法的合理性.
此外,由图2、图3 亦可见,若不考虑土的成层性,前排桩在桩顶部分侧向位移会偏大,在桩底会偏小.这是由于不考虑土的成层性,利用加权平均计算一个假想的单一土层的参数,在桩顶部分会过高估计桩土相互作用,使得桩顶部分侧向位移偏大,反之在桩底部分则会低估桩土相互作用使得桩底位移偏小.后排桩的侧向位移在不考虑土层成层性的情况下,侧向位移趋势与本文结果基本一致,但是在数值上较考虑土的成层性增大了10%~20%.由此可见:地基土的成层性对双排桩支护结构的受力变形有较大影响,在相关设计计算时需考虑地基土的成层性.
4 结论
本文基于Euler-Bernoulli 双层地基梁理论,对成层地基中的双排桩支护结构的受力变形进行了分析.本文方法具有如下优点:
1)可考虑地基土的成层性、桩土相互作用、前排桩的设置对后排桩受力变形的影响以及地基反力系数随土层的变化.
2)将前、后排桩分别视为竖向放置的弹性结构,将桩身穿过的地基土理想为水平向的弹性均质体,以不同刚度的水平弹簧模拟前、后排桩与其间成层地基土体的相互作用,借此来完成前、后排桩的相互作用力的传递和变形协调.
3)获得了前、后排桩支护结构各微段的位移与内力的幂级数解答.
采用本文方法对某工程实例进行分析,并与实测值进行对比表明,本文方法计算结果在一定程度上能够反映双排桩支护结构的侧向位移趋势,并且较不考虑土的成层性更接近于实测值,说明本文的计算方法具有一定的可行性.但是对于复杂的地下结构,土与结构共同作用以及土体的非线性行为等都对支护结构的变形有着很大的影响,双排支护结构桩桩、桩土相互作用过程极为复杂,因此相关研究工作仍有待进一步深入.

