斜交桥对河道行洪的影响分析

涂 进，胡 立，武 剑，连雷雷

（1.长江水利委员会汉江水文水资源勘测局，湖北 襄阳 441022；2.云南省水文水资源局楚雄分局，云南 楚雄 675099）

1 研究背景

随着国民经济的发展，跨河桥梁日渐增多，桥梁工程涉河建筑物对河道行洪的影响问题日渐突出。我国公路桥梁设计通用规范要求，桥梁纵轴线宜与洪水主流向正交[1]，但由于受到现场地形、河势及地质条件等诸多因素的限制，部分桥梁工程建设过程中，桥梁与主流向存在一个夹角，当该夹角较小时，可近似认为桥梁与河道正交，现有的桥渡公式均针对该正常工况下，但若该角度较大，则在分析桥梁修建对河道的影响时，若直接采用桥渡公式进行计算，则会存在一定的误差。早在上世纪80 年代，曹瑞章等通过水工模型试验及收集野外观测资料，分析了斜交桥桥前壅水和墩前冲高的特点[2]；王仁宽等针对山区斜交桥桥下过水面积、水位、壅高、墩前冲高和冲刷等问题，针对投影法计算公式存在的缺陷，提出了自己的研究成果与计算方法[3]。

传统的水工模型试验受客观条件限制较大，随着数值模拟技术的发展，根据河道地形资料及桥梁工程涉河建设方案，构建河道数学模型，可以进行壅水等相关分析，并与传统公式法技术成果进行对比分析，以更准确地评价桥墩对河道行洪造成的不利影响。

2 研究区域

受到实际工作条件所限，本文采用假设法进行分析计算，即假定一工程河段，当桥梁修建时分别采用不同的夹角，分析现有公式的适用性。

为了减小地形的误差，本次构建一条天然明渠，渠道为梯形河槽，底宽15 m，顶宽25 m，边坡比为1∶1，河底进出口高程分别为62 m～61.5 m，河槽长度为2 km，桥梁工程位于纵断面桩号0+400 处，分别进行不同斜交角度工况条件下桥梁的壅水数值分析。桥梁在河道内自左而右布设有1#～4#共4 个圆柱桥墩，桥梁轴线与河道斜交角度分别为30°、45°、60°，由于斜交角度越大，桥墩平面间距越大，三种情况下桥墩投影至垂直断面上与正交条件下桥墩相重合，单个桥墩直径为1 m。

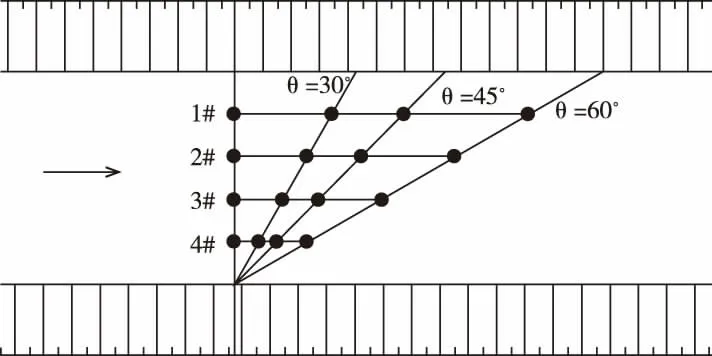
图1 工程河段桥墩布设示意图

3 桥梁壅水计算

（1）正交条件下

桥梁上游壅水是水流动能转化为势能的结果，根据规范推荐公式，桥前最大壅水高度可用下述公式计算[4]：

其中：K 为壅水系数，K=KN·KV分别为建桥后、建桥前桥下平均流速；Kp为考虑冲刷引入的流速折减系数。为考虑冲刷引入的流速折减系数；本次假定河道为混凝土衬砌，因而不考虑冲刷带来的流速折减，壅水修正系数KV=1，故壅水系数直接采用定床壅水系数，若桥梁轴线与河道水流方向为正交，根据公式可计算得到桥前最大壅水高度。

（2）斜交条件下

由于上述公式未考虑桥梁轴线与河道为斜交，故而上述公式不能直接用于斜交桥的桥前壅水高度计算。当前用于斜交桥壅水计算主要有投影法以及王仁宽等人总结的斜交公式等。

投影法即桥下净过水面积等于两岸桥台边墙间的距离在垂直于水流断面上的投影，再扣掉所有桥墩在该断面上的投影之和，即将所有构筑物均投影至同一断面上，再以该断面作为基准，进行桥墩的阻水分析。该方法计算较为简便，但是该方法认为水流总是垂直于断面方向自上而下流动，而忽略了水流遇到桥墩时侧向流的产生，因而采用该方法计算得到的桥墩阻水面积相比实际情况有所偏大，且偏大程度随斜交角度的增大而增大，且在特定条件下，桥下过水面积有可能出现负值。

投影法桥下有效过水面积分析采用下式：

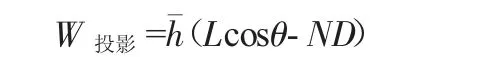
采用王仁宽法进行计算，王仁宽法主要针对桥下有效过水面积进行重新计算，其桥下有效过水面积分析采用下式：

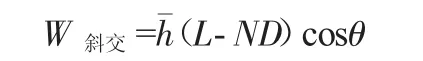
桥前最大壅水高度采用下述公式：

（3）计算示例

以桥梁与水流方向斜交30°为例，流量采用136 m3/s，采用上述公式进行壅水计算。

工程前桥位处过水面积为81.6 m2，工程后采用斜交法桥下有效过水面积计算公式，可得W斜交为66.4 m2，进而可得桥前最大壅水高度为0.11 m，考虑修正系数，则修正后桥前最大壅水高度为0.27 m。

工程前后桥位断面处水流特征值见表1。

表1 斜交角度30°时桥位断面水流特征值

根据上述公式，分别对桥梁与水流方向正交、以及斜交角度为30°、45°、60°这几种情况进行壅水计算，其中斜交条件下由于桥墩投影至垂直断面处与正交条件下桥墩相重合，因而正交壅水计算结果即为投影法壅水计算结果，计算结果见表2。

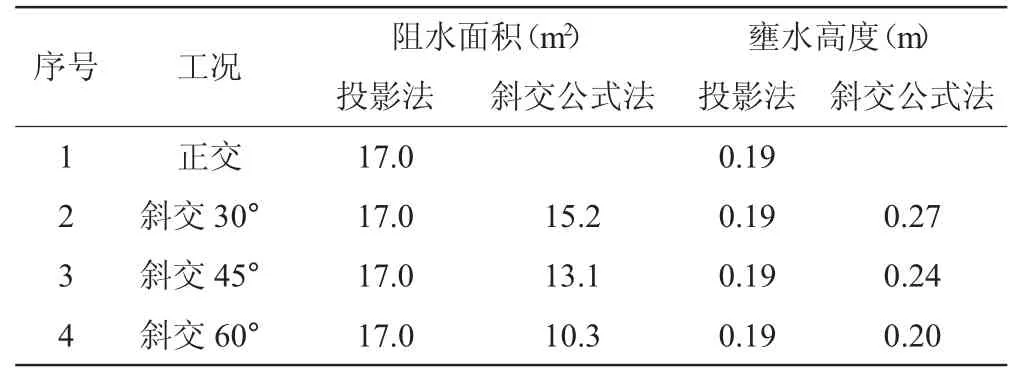
表2 不同斜交角度下桥墩壅水计算结果（公式法）

4 数值模拟分析

数值模拟软件采用Mike21 二维水动力数学模型，根据河道地形资料进行网格概化，对桥位所在河段进行建模，分析计算工程后对河道的壅水及其流速场变化，其在平面二维自由表现数值模拟方面具有强大的功能[5]，模型所得结果可以用于洪水区域管理以及洪水安全研究分析。为了保证边界条件的一致性，减小工程前后下游边界条件的改变，上游进口流量采用136 m3/s，下游出口水位设为65.60 m。

为了分析壅水数值与斜交角度大小的变化关系，分别对桥墩与河道正交、斜交30°、45°、60°工况条件下进行模拟计算。图2、图3 分别为斜交30°和斜交60°工况条件下的流场分布图，从图中可以看出，斜交角度越小，由于桥墩间距较小，对水流的压缩越显著，而随着斜交角度的增大，桥墩间距随之增大，由于侧向流的存在，桥墩间过流能力越大。理论上，当斜交角度增大到极限，即斜交角度无限接近90°时，则桥梁轴线接近于平行河流顺河布设，此时桥墩间距也被无限拉长，桥墩之间水流相互干扰越小。

图2 斜交30°局部流场分布图

图3 斜交60°局部流场分布图

不同工况条件下的工程前后水位及桥前壅水高度计算结果见表3，从表中可以看出正交工况下，壅水高度最大，随着斜交角度的增大，壅水高度逐渐减小；桥墩上下游水头差见表4，对于不同的斜交角度，上下游水头差随斜交角度的增大而减小，从横向分布上，由于斜交桥的挑流效应，愈靠近下游桥墩上下游水头差越大，相应流速亦越大。

表3 不同斜交角度下桥墩壅水计算结果（数学模型法）

表4 不同斜交角度下桥墩下游壅水计算结果（数学模型法）

5 对比分析

将分别采用公式法及数学模型法计算得到的不同斜交角度工况下的壅水计算成果进行对比分析，可以看出，由于不同的斜交角度工况下，桥墩投影均有正交工况条件下相重合，因而投影法计算均为一定值，这与实际情况是不相符的；王仁宽等人提出的斜交公式法，考虑了侧向流的存在以及不同的斜交角度对壅水的影响因素，当斜交角度越大，壅水效应越小，这与实际情况是相符的，与数学模型分析法相比，其计算成果存在一定的误差，但误差较小，基本可以适用于常规的分析计算以及洪水安全研究分析。

6 结语

本次分别采用投影法及王仁宽等人提出的方法，对不同斜交角度桥梁的壅水进行分析，并与数学模型模拟计算进行对比验证，通过以上分析计算，可以得到如下结论：

（1）规范推荐公式仅可适用于常规工况下，即桥梁轴线与河道基本垂直，或斜交角度较小时；对于斜交角度较大时，若采用投影面积法计算桥下净过流面积，其成果相比实际情况偏小，且随着斜交角度的增大，误差越大。

（2）对于王仁宽等提出的斜交公式，该方法考虑了侧向流的存在，所计算桥下净过流面积较投影法更接近实际情况，根据其推导的壅水公式所计算的桥前壅水，随斜交角度增大而减小，通过其与二维数学模型法成果相比，其计算成果基本合理。

（3）从横向分布上，由于斜交桥的挑流效应，靠近下游桥墩局部流速较大，对桥台及岸坡的冲刷效应明显。

（4）相比于公式计算，数学模型法可更真实的反应地形地貌、河势及工程具体布设，且可获取的流场分布、局部壅水等要素成果更为丰富，但其对所需要的地形资料要求较高，在条件允许的情况下，可优先选用数学模型法进行桥梁等涉水工程的壅水分析。