DIC应变测量的局部平滑去噪算法研究

钱 坪，徐飞鸿，张 樟，刘林修

（长沙理工大学土木工程学院 长沙410114）

0 引言

传统的接触式测量方法应用比较广泛，有很多优点。但也有一些缺点，例如面对微小试件或高温环境，此方法显然难以胜任，需要一种非接触的乃至全场的结构变形测量技术。自1980年Yamaguchi［1］和Peters［2］提出数字图像相关方法（Digital Image Correction，简称DIC）至今，DIC理论研究与工程应用都取得了令人欣慰的成果。1985年，Chu等人［3］建立被测物体表面位移与应变的关系式，完善了数字图像相关方法。1989 年，Bruck 等人［4］采用Newton-Raphson 法实现了基于亚像素的相关搜索，使DIC方法更趋成熟。国内方面，1985年，高建新［5］利用电镜对铸件大变形的测量应用研究，将DIC测量技术推广到了微观测量领域；2000年，王琛影等人［6］提出曲面拟合法求解亚像素位移方法，进一步推动了DIC方法的深入研究；2007年，潘兵等人［7］提出一种基于位移场局部最小二乘法求解应变的方法，能更好的提取应变信息。2013年，徐飞鸿等人［8］基于结构离面位移和其散斑应变场的线性对应关系，进行了亚像素级DIC离面位移测量；2017年，严盛龙等人［9］运用经典的计算机图像边缘识别技术结合DIC亚像素精度的Gauss⁃ian曲线拟合，成功地提取了混凝土表面裂缝的边缘特征，改进了裂缝宽度测量方法。2020年，吴荣等人［10］在传统DIC应变计算方法基础上引入变形前后的旋转矩阵，提出一种考虑旋转的局部位移场最小二乘应变计算方法。随着数字图像相关方法理论研究的成熟发展，该方法在力学、土木等领域得到了广泛的应用［11，12］。

结构的应变是工程结构受载响应的主要指标之一，是结构分析或结构测试不可回避的重要参数。根据弹性力学，直观上可对DIC 获得的位移场进行差分计算便可求解应变［13］，但是由于位移场的噪声以及差分计算引起噪声，必然导致由此测得的应变信息缺乏可信度［14］。对位移场采用全场最小二乘拟合再计算应变显然有其合理性，但工程结构的变形状态未知、变形的复杂性，决定了该方法中构造合适的拟合函数［15］仍是个难题；目前普遍认为对位移场可采用局部最小二乘再计算应变［7，16］，它可在拟合的过程抑制噪声从而提高应变测量精度。这一方法理论简单、编程方便、运行高效，还可避免全场最小二乘拟合时选择拟合函数选择的困窘。本文基于DIC 应变测量局部二乘拟合的应变测量算法，分析位移场算法的误差，采用局部加权回归散点平滑技术结合，研究应变测量的“局部化”算法、提高DIC应变测量精度。

1 DIC应变测量原理

1.1 数字图像相关方法

被激光照明的物体，其表面呈现颗粒状结构，即散斑。物体的位移或变形必然引起散斑场的变化，数字图像相关方法就是利用采集设备采集试件变形前后的散斑图像，然后通过计算分析实现位移测量。

DIC 的基本原理如图1 所示，对变形前图像中一定的区域进行网格划分，选取以某待求点（x0，y0）为中心的计算子区；然后按预先定义的相关函数，通过搜索方法来进行相关计算，找到变形后图像中与该子区关联最大的区域，其中心为（x0′，y0′），这就是该子区域在变形后的位置；由此计算出图像子区中心点的x和y方向的位移分量u、v。

图1 变形前后图像子区示意图Fig.1 Image Sub Region before and after Deformation

1.2 非均匀变形模式下的Green应变

根据DIC 基本理论，非均匀变形模式下，位移形函数即位移拟合函数可用二维二次多项式描述：22

值得注意的是影响应变计算精度中最主要的一个因素是亚像素位移测量精度。比较各种DIC 亚像素位移测量算法（曲面拟合法［6，18］、梯度法［19，20］、New⁃ton-Rapson 法［6，17］），不难发现Newton-Rapson 法的计算精确度更高、结果更为准确，本文也将采用这一广为应用的算法来研究平滑去噪方法。

2 基于局部化平滑去噪的应变测量

2.1 位移测量误差与平滑去噪技术

用计算机生成2 幅未添加噪声的散斑图，如图2所示，其中一幅在x方向上施加200 με 均匀应变模拟变形后的散斑图像。由Newton-Rapson 法计算散斑图变形后的位移场，采用局部最小二乘拟合法求解应变值。计算所得的位移场和应变场如图3a、图3b 所示，其结果不甚理想。

图2 均匀应变模拟散斑图Fig.2 Simulated Speckle Pattern of Uniform Strain

图3 Newton法计算的位移及对应应变Fig.3 Displacement and Corresponding Response Calculated by Newton Method

模拟散斑图2a 所施加的变形仅是x方向的，y方向在理论上没有变形。随机抽取同一x处的一列数据点，如图4 所示，y方向位移数据在理论值附近波动，其中部分计算点数据偏差过大，有必要进行简易滤波处理，去除部分偏差较大计算数据并用均值代替（5个偏大值点，5个偏小值点），来达到平滑去噪的目的。

图4 某x处沿y方向位移计算值和理论值Fig.4 Calculated and Theoretical Displacement Values along x Direction at y

对平滑去噪处理后的位移场，重新按局部最小二乘法求解应变。处理后重新所测得的位移场和应变场如图5所示。

不难发现，由平滑去噪处理后的位移场所测得的应变场波动幅度更小、更为接近应变真值、应变测量精度有所提升，表明此处平滑去噪有效降低了位移场求解计算引入的噪声。所以，探索更为有效的平滑去噪手段、对位移场进行恰当处理、消除计算过程包括散斑图获取过程引入的噪声，对于提高应变测量精度非常重要。

图5 滤波后的位移及对应应变Fig.5 Displacement and Corresponding Strain after Filtering

2.2 基于局部加权回归平滑去噪技术

2.1 节表明平滑去噪处理有助于提高应变测量精度；文献［22］对位移场进行x，y两个方向的三次样条函数平滑处理，获得了较好的应变计算结果。本文基于局部加权回归平滑法，利用其线性回归简单性和非线性模型灵活性的特点，研究其平滑去噪提高应变测量精度的可行性。

首先，注意到实际结构位移场的复杂性，考虑与应变计算的局部最小二乘拟合法相适应，也采用局部化的策略先进行平滑去噪处理，即：选定合适的计算窗口、在位移场全场中选取窗口中局部数据进行拟合；对窗口内和它相邻近的数据进行加权回归，得到每一计算窗口中的中心点的数值：权重与要求解的中心点距离成反比；不断移动窗口，依次根据下一计算窗口内的数据计算其中心，直至计算完全部区域；面向实际结构的复杂应变场，计算过程中位移形函数选取二次多项式，局部化平滑滤波处理的策略充分考虑位移场的复杂性来获取更真实的位移场数据，即必要时允许在相邻的局部区域选取不同的回归方程。可见，计算窗口大小的选取会影响到拟合的光滑程度，窗口越大位移场越平滑，但窗口过大可能使部分数据失真。因此，怎样选择拟合窗口非常重要。

对图3a 进行局部加权回归平滑去噪后处理的位移场如图6a所示，局部化平滑滤波处理后的位移场光滑平整，十分接近于理论位移场，与图6b 采用三次样条拟合去噪处理的位移场结果相比较，其边缘角点处的位移更为真实。

图6 局部化平滑去噪效果Fig.6 Effect of Local Smoothing and Denoising

2.3 应变测量的局部化算法

考虑到结构变形的复杂性，位移形函数采用二阶多项式，经过局部化的平滑去噪处理后，可以很好地控制位移场的噪声，同时使用局部最小二乘拟合法来计算应变，形成基于局部加权散点平滑去噪（LOW⁃ESS）的应变测量算法。

结合文献［21］的LOWESS 算法，基于LOWESS 函数的应变测量算法具体步骤如下：①对计算区域进行合适的局部化划分，分割出若干计算子区；②在计算子区中，对指定的计算窗口内各个数据点的初始权重赋值，权重函数可选用数值之间欧氏距离比值的立方函数；③利用初始权重进行回归估计，利用估计式的残差定义稳健的权函数并计算新的权重；④利用新的权重重复步骤②，继续修正权函数，直至收敛；⑤根据拟合多项式和权重得到任意点的光滑值；⑥根据步骤①计算区域的局部化，采用最小二乘拟合法计算应变值。

图7 给出了文献［22］三次样条函数平滑处理的最小二乘拟合结果，三次样条函数平滑处理位移场后能降到22 με，局部化平滑滤波处理后下降到12 με。显然本文方法效果更优。

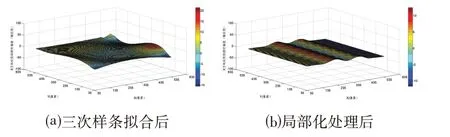
图7 平滑去噪处理后应变场效果Fig.7 Strain Field Effect after Smooth Denoising

3 非均匀应变场测量

受荷载作用或环境状态改变的工程结构，其位移场或应变场因往往呈现出极为复杂的状态。为了有效模拟实际应变测量，考虑非均匀场的应变测量。

采用2.1 节同样的方法制作模拟散斑图，生成两幅未添加噪声的线性变化的非均匀应变变形散斑图，在变形后散斑图像x方向上施加ux=0.25x微应变量的非均匀变形。

对变形前后的两幅数字散斑图，采用Newton-Rapson 方法准确计算亚像素位移，并用局部最小二乘拟合求解应变，得到的位移场和应变场如图8 所示。三次样条拟合和局部平滑去噪的应变场如图9所示。

表1比较了3种方法输出的最大值、最小值、绝对误差和标准差。结果显示，局部平滑去噪后计算结果整体上最为接近真实的理论应变值，误差分布更为合理，说明该方法可以用于非均匀应变变形计算。

图8 Newton法计算的位移及直接计算的应变Fig.8 Displacement Calculated by Newton Method and Strain Calculated Directly

图9 平滑去噪效果Fig.9 Smooth Denoising Effect

表1 应变测量值比较Tab.1 Comparison of Strain Measurements

4 结语

本文研究局部平滑去噪与最小二乘拟合的应变测量算法，提高数字图像相关应变测量精度。

⑴DIC位移测量的数值计算过程的误差，是最小二乘拟合应变计算的主要误差来源之一。为了避免应变测值失真，应将精细计算的位移场再进行平滑去噪、抑制误差；

⑵选择非均匀变形二阶形函数，应用Newton-Rapson 法求解位移场，通过局部加权回归对位移场施行平滑去噪，结合局部最小二乘拟合求解应变场。本文局部平滑去噪与最小二乘拟合的应变测量算法具有线性回归简单、非线性模型灵活的特点，去噪效果明显、编程简便，可用于复杂应变场的测量；

⑶本文算例模拟噪声污染的复杂应变场测量，结果展示了本文方法的有效性。但此类方法计算“小应变”时抗噪能力不强，有待改进。