多故障网络控制系统鲁棒H∞容错控制
赵千钧,付兴建
(北京信息科技大学 自动化学院,北京100192)
0 引言
网络控制系统(NCS)是由控制器、传感器和执行器等部件通过通信网络连接构成的闭环系统。各学科领域之间相互交叉渗透,控制系统变得越来越复杂、被控对象越来越多元化,在此背景下网络控制系统得到了快速的发展。但网络控制系统在通过共享网络信息资源实现控制而带来各种优越性的同时,也存在受网络通讯带宽限制而产生的网络延迟、数据包丢失、网络阻塞等问题。容错控制就是在控制系统发生故障的情况下设计控制器,使系统保持其稳定性。
T-S模糊模型在逼近和描述非线性复杂系统方面是一种有力的工具。模糊理论的提出,开辟了用数学方法处理自然界中不确定现象的新途径。近年来大量研究者利用T-S模糊模型对非线性系统进行建模,在此基础上研究非线性系统的容错控制问题具有重要的工程意义[1]。
与此同时,网络控制系统的容错控制得到了高度重视并取得了一些成果[2-4]。文献[5]针对不同的外部噪声类型,选取不同的性能指标,逐步深入地对分布时滞网络控制系统鲁棒控制器设计问题展开研究。文献[6]研究了传统容错控制方法难以保证非线性系统在执行器和传感器多故障并发情形下的稳定性问题。文献[7]考虑带有执行器故障和分布时滞的网络控制系统,研究了一类鲁棒容错H∞控制器的设计问题。文献[8]针对具有时滞时变的非线性网络控制系统,研究了基于离散事件触发方案的主动和被动容错控制问题。
目前的研究大都仅单一地分别针对执行器或传感器故障设计容错控制器以保障系统稳定[9]。然而在复杂的实际控制系统中,多处执行器和传感器故障完全可能同时并存,因此针对单一类型故障设计得到的容错控制器就不一定能够稳定多类别故障并发系统,存在较大安全隐患。文献[10]考虑了状态不可测时一类网络切换系统的鲁棒H∞控制问题,针对既有传感器失效,又有执行器失效的故障情况,设计了一种状态反馈控制器。
本文针对含有数据丢包和时延的网络控制系统,对执行器以及传感器同时出现故障的情况,建立了针对系统的故障模型。结合Lyapunov稳定理论和Schur补引理以及状态反馈的有关知识,推出满足传感器和执行器均出现故障但仍能稳定运行的条件,并通过LMI工具箱计算出关于状态反馈的系数,设计出有效的具有鲁棒特性的容错控制器。最后通过算例证明了方法的可行性。
1 T-S模糊模型的建立
考虑下述由T-S模糊模型近似描述具有参数不确定性的非线性时延网络控制系统,第i条模糊规则可表示如下。
如果θ1(t)是Mi1,并且θs(t)是Mis,则:
(1)
式中:x(t)为状态向量;u(t)为控制输入向量;y(t)是被控输出向量;ω(t)为外界扰动;i=1,2,…,r,r为模糊规则数;θ1(t),θ2(t),…,θs(t)为前提变量,Mij(i=1,2,…,r;j=1,2,…,s)是和规则数相对应的模糊集合;Ai,Bi,Ci,Di,Bli为有适当维数的实值常数矩阵;ΔAi和ΔBi是具有时变特征的不确定参数矩阵且具有如下结构:
[ΔAiΔBi]=GP(t)[UaiUbi]
(2)
式中:G、Ua和Ub为已知适当维数常值矩阵;P(t)为不确定矩阵,满足:
PT(t)P(t)≤I
(3)
2 故障模型的建立
针对执行器故障和传感器故障,用矩阵F表示可能的执行器故障模式,其形式为
F=diag{f1,f2,…,fm}
当fi=0时,表示第i个执行器完全失效;当fi=1时,表示第i个执行器正常工作;当0 用矩阵M表示可能的执行器故障模式,其形式为 M=diag{m1,m2, …,mn} 当mj=0时,表示第j个执行器完全失效;当mj=1时,表示第j个执行器正常工作;当0 执行器出现故障时,带故障的状态方程为 (4) 传感器出现故障时,带故障的状态方程为 (5) 执行器和传感器同时出现故障时,带故障的状态方程为 (6) 则在网络时延和丢包环境中,多故障并发时反馈控制器为 uf(t)=FKiMx(t) (7) 采用单点模糊化、乘积推理以及加权平均反模糊化的方法,可得系统的整个状态方程为: t∈[qkh+τk,qk+1h+τk+1),k=1,2,… (8) 式中: θ(t)=[θ1(t),θ2(t),…,θs(t)] 从现实网络环境出发,可以假设存在常数η≥0,使得 (qk+1-qk)h≤η (9) 定义1考虑网络环境中,多故障系统满足如下2个条件: 2)在零初始条件下,对给定的H∞扰动抑制水平γ及任意的外界扰动ω(t)∈L2[0,∞),控制输出y(t)满足: (10) 则称系统式(6)是鲁棒渐近稳定的,且具有H∞范数界γ。 引理1[11]对矩阵Xi和Yj(1≤i≤r),以及适当维数矩阵S>0,下述不等式成立: (11) 1)S<0 引理3[11]设x(t)具有一阶连续导数,对任意矩阵R=RT>0和M1、M2,以及标量函数τ≥0,有以下不等式成立: τξT(t)YTR-1Yξ(t) (12) 式中:ξ(t)=[xT(t)xT(t-τ)]T,Y=[M1M2]。 (13) 式中: Ξ44= 则存在控制器式(7)使得闭环系统式(8)鲁棒渐近稳定。 证明构建Lyapunov-Krasovsk泛函 (14) 则V(t)的导数为 xT(t-τm)N1x(t-τm)- t∈[qkh+τk,qk+1h+τk+1),k=1,2,...,n (15) 对式(15)中积分项根据引理3,有下列积分不等式成立: (16) (17) (18) (19) 式中: ξ1(t)=[xT(t)xT(t-τm)]T ξ2(t)=[xT(t)xT(t-η)]T ξ3(t)=[xT(t-τm)xT(qkh)]T ξ4(t)=[xT(qkh)xT(t-η)]T 由引理1可知: [Cix(t)+DiFKjMx(qkh)] (20) 将式(16)~(19)代入式(15),并结合式(20)可推出: (21) 式中: 当ω≡0时,可得 (22) 式中: ←xT(t-τm)xT(t-η)]T ζ=[CiDiFKjM0 0] (23) 由式(23)可知,φij<0时系统渐近稳定。 同时可得 (24) 从qkh+τk到t∈[qkh+τk,qk+1h+τk+1)对式(24)两边进行积分,即: (25) 令t→∞,在零初始条件下可得 (26) 综上所述,根据定义当Φij<0,系统鲁棒渐近稳定,且满足H∞范数界γ。 下面证明式(13)成立和Φij<0等价。由Schur补定理可知Φij<0等价于: (27) 式中: β11= (28) 式中: φ1=[(WG)T0 0 0 0]T φ2=[UaiUbiF0KjM00 0 0] Λ1=[0KjM00 0 0]T ← 0 0 0 0] 根据引理4可知,存在α1>0,α2>0使得如下不等式成立: (29) 不等式左侧乘: 针对T-S模糊NCS模型,选取模糊数据: 现分几种情况进行讨论。 故障类型1:考虑执行器故障的情形,令反馈控制控制器uf(t)=FKiMx(t)中的M=I。无外部扰动时,系统状态响应仿真曲线如图1所示;存在外部扰动信号ω(t)=0.5 sin(2πt)时,系统状态响应仿真曲线如图2所示。 由图1可以看出在执行器发生故障且没有外部扰动时,系统在1~2 s趋于稳定;图2是当系统加入外部扰动ω(t)=0.5 sin(2πt)时,设计的容错控制器同样能使系统快速趋于稳定,针对系统发生单一的执行器故障,控制器具有很好的控制效果。 故障类型2:考虑传感器故障的情形,令反馈控制控制器uf(t)=FKiMx(t)中的F=I。无外部扰动时,系统状态响应仿真曲线如图3所示;存在外部扰动信号ω(t)=0.5sin(2πt)时,系统状态响应仿真曲线如图4所示。 由图3可以看出在传感器发生故障且没有添加外部扰动时,系统在2 s附近趋于稳定;图4是当系统加入外部扰动ω(t)=0.5sin(2πt)时,设计的容错控制器能使系统在2 s附近趋于稳定,控制效果较理想。 故障类型3:考虑执行器和传感器同时失效故障的情形,令反馈控制控制器uf(t)=FKiMx(t)中的F=M=0.75。无外部扰动时,系统状态响应仿真曲线如图5所示;存在外部扰动信号ω(t)=0.5sin(2πt)时,系统状态响应仿真曲线如图6所示。 由图5可以看出在执行器和传感器同时失效且没有外部扰动时,系统在1~2 s趋于稳定;图6是当系统加入外部扰动ω(t)=0.5sin(2πt)时,设计的容错控制器能使系统在2~3 s趋于稳定,具有很好的控制效果,满足本文的设计要求,从而验证了结论的合理性和可行性。 从图1~6可以看出,3种故障类型的状态x1和状态x2的响应曲线都能达到收敛效果,最终稳定。无论是考虑单一故障还是多故障,所设计的NCS的容错控制器均能达到很好的控制效果,使控制系统在出现故障的情况下仍然能够达到稳定的状态,且具有一定的抗扰动性能。 本文针对执行器和传感器同时失效的故障情况,建立了一类同时具有不确定时延和丢包的网络控制系统故障模型,研究了一类非线性 NCS 的模糊H∞容错控制器设计问题;利用了网络化 T-S 模糊模型去逼近此类非线性 NCS;给出了时延、丢包、执行器和传感器同时失效的故障情形下模糊控制器存在的充分条件。并对网络控制系统的鲁棒容错控制进行了分析,给出了控制系统的渐近稳定的充分条件,设计了鲁棒容错控制器。进行了数值仿真验证了结论的合理性和可行性。
3 控制器设计
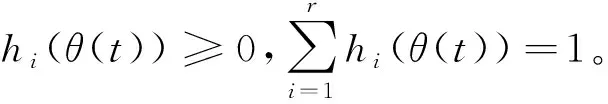

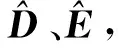

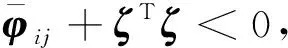
4 算例仿真
5 结束语

