Correlation-driven topological phase transition from quantum anomalous Hall insulator to Mott insulator in monolayer VCl3 and VBr3*

XU Yongfeng, SHENG Xianlei, ZHENG Qingrong†

(1 School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China; 2 Key Laboratory of Micro-NanoMeasurement-Manipulation and Physics of Ministry of Education, Department of Physics, Beihang University, Beijing 100191, China)(Received 26 March 2019； Revised 8 May 2019)

Abstract Based on the first-principle calculations, we propose that the monolayer VCl3 and VBr3 are quantum anomalous Hall insulators with in-plane magnetization without considering the correlation effect of the 3d electron-electron interaction. The band gap is predicted to be about 3.4 meV for VCl3, but no global gap for VBr3. It is interesting to note that VCl3 (VBr3) possesses a Chern number of C=3 (C=1) with three (one) chiral edge states. After considering correlation effect, we obtain Mott insulator if U>0.45 (U>0.35) eV for VCl3 (VBr3).

Keywords ferromagnetic semiconductor; large Chern number; Mott insulator

Since the discovery of quantum Hall (QH) effect, the study of the topological phase of matter has attracted great attention in the condensed-matter community. A voltage caused by the deflected motion of charged particles under external electric field and magnetic field leads to the quantized Hall conductance[1]. Nevertheless, the quantum Hall effect may be achieved without external magnetic field. In 1988, Haldane[2]proposed the quantum anomalous Hall (QAH) effect in a two-dimensional (2D) honeycomb lattice with next-nearest-neighboring hopping modulated by staggered flux. Dissipative boundary states exist in the two edges of materials with QAH effect[3-5]. The anomalous Hall effect has an intrinsic origin due to spin-dependent band structure of conduction electrons, which can be expressed in terms of the Berry phase or Chern number in the momentum space[6]. This effect originates from the coupling of electron orbital motion to its spin, i.e., spin orbit coupling (SOC), resulting in the opposite motion of electrons with spin-up and spin-down. In a ferromagnetic metal, the magnetization causes an imbalance in the population between the electrons with spin-up and spin-down and consequently leads to the anomalous Hall effect. Considering the time reversal (TR) symmetry, the quantities of electrons moving in the opposite directions with different spins are equal and as a result there is no charge Hall conductance, but a nonzero spin Hall conductance exhibits quantum spin Hall (QSH) effect[7]. The QAH insulator[8]was a recently discovered topological electronic phase where strong SOC and ferromagnetic ordering conspire to generate a band gapEgin the bulk of a two-dimensional (2D) electron system, as well as conducting gapless chiral edge states in its boundaries. The edge states are robust against impurities or disorders because the electron backscattering in the two edge channels is prohibited due to the TR symmetry. Topologically nontrivial band structure is characterized by a nonzero Chern number by counting the number of edge states. The QAH effect not only occurs in out-of-plane magnetization systems[9-15], but also exists in in-plane magnetization materials[16-21].

The layered transition-metal trichlorides materials of MCl3(M=Ti, V, Cr, Fe, Mo, Ru, Rh, Ir) have been achieved for many years due to relatively weak van der Waals interaction between the interlayers[22-25]. These layered materials, which possess honeycomb lattice, partially occupiedd-orbitals, and nonnegligible SOC, may have interesting properties, and thus they are worth studying.

1 Computational methods

The first-principle calculations were performed within the Viennaabinitiosimulation package (VASP) using the projector augmented wave (PAW) method in the framework of density functional theory (DFT)[26-28]. The electron exchange correlation functional was described by the generalized gradient approximation (GGA) in the form proposed by Perdew, Burke, and Ernzerhof (PBE)[29]. The lattice parameters are chosen from Springer Materials[30]. The structure relaxation considering both the atomic positions and lattice vectors was performed by the conjugate gradient (CG) scheme until the maximum force on each atom was less than 0.01 eV/Å(1 Å=0.1 nm), and the total energy converge threshold was 10-6eV with Gaussian smearing method. To avoid unnecessary interactions between the monolayer and its periodic images, the vacuum layer was set as 20 Å. The energy cut off of the plane waves was chosen as 520 eV. The Brillouin zone (BZ) integration was sampled with a 9×9×1 G-centered Monk horst Pack grid. The relaxed lattice parameter (a=6.012 Å) was adopted in the calculations. SOC is included by a second variational procedure on a fully self-consistent basis. An effective tight binding Hamiltonian based on the maximally localized Wannier functions (MLWF) was used to investigate the surface states[21,31]. The iterative Greens function method[32]was used with the package WannierTools[33].

2 Results and discussion

The two-dimensional VCl3(VBr3) consists of a V atomic layer sandwiched by two Cl atomic layers. The V atoms form a honeycomb lattice and each V atom is surrounded by six Cl atoms, which forms an octahedral crystal field, as shown in Fig. 1. It takes the same structure as monolayer OsCl3that has been shown to be an intrinsic quantum anomalous Hall insulator[34]. V is a transition metal element with partially filled3d-orbitals, which may result in magnetism. Based on the first-principle calculations, we consider several magnetic configurations, including ferromagnetic (FM), antiferromagnetic (AFM), and paramagnetic (PM) states. We firstly take VCl3as an example and find that VCl3takes the FM ground state with in-plane magnetization along zigzag direction as shown in Table 1.

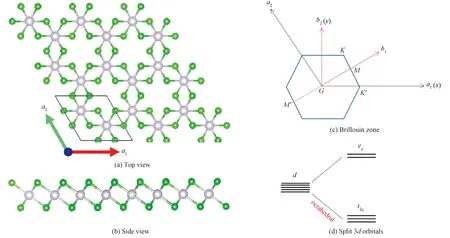
Fig.1 Top (a) and side (b) views of monolayer VCl3, first Brillouin zone(c) of monolayer VCl3 withdirect reciprocal lattice vectors and the high symmetry points indicated, and 3d orbital splitting under octahedral crystal field (d)

Table 1 FM and AFM energies of VCl3

The band structure calculations show that VCl3is a fully spin-polarized half metal. Without considering SOC, it is a 2D Weyl half semimetal with a band crossing point in eachG-Mpath, such that there are total 6 Weyl points in the first BZ. After turning on SOC, a band gap of about 3.4 meV was opened, and the material becomes a ferromagnetic semiconductor, which is different from PtCl3which is a 2D Weyl half semimetal even with SOC due to additional symmetry protection[35]. To understand these features, we find that under the octahedral crystal field formed by Cl atoms, V-3dorbitals are split intot2gandegorbital groups, and the latter is higher in energy. For each V3+with two valence electrons, there are four valence electrons in one primitive cell, such that V-t2gorbitals will be partially filled in one spin channel. The othert2gspin channel and allegorbitals are empty. Therefore, the system is half Weyl semimetal without considering SOC. If turning on SOC, thet2gorbitals will split intoj=1/2 doublet state andj=3/2 quartet state with the former energetically higher, such that the system becomes a semiconductor, as shown in Fig. 2. The topologically nontrivial band structure of VCl3may come from the combination effect of honeycomb lattice formed by V atoms and the SOC of transition metal V atoms.

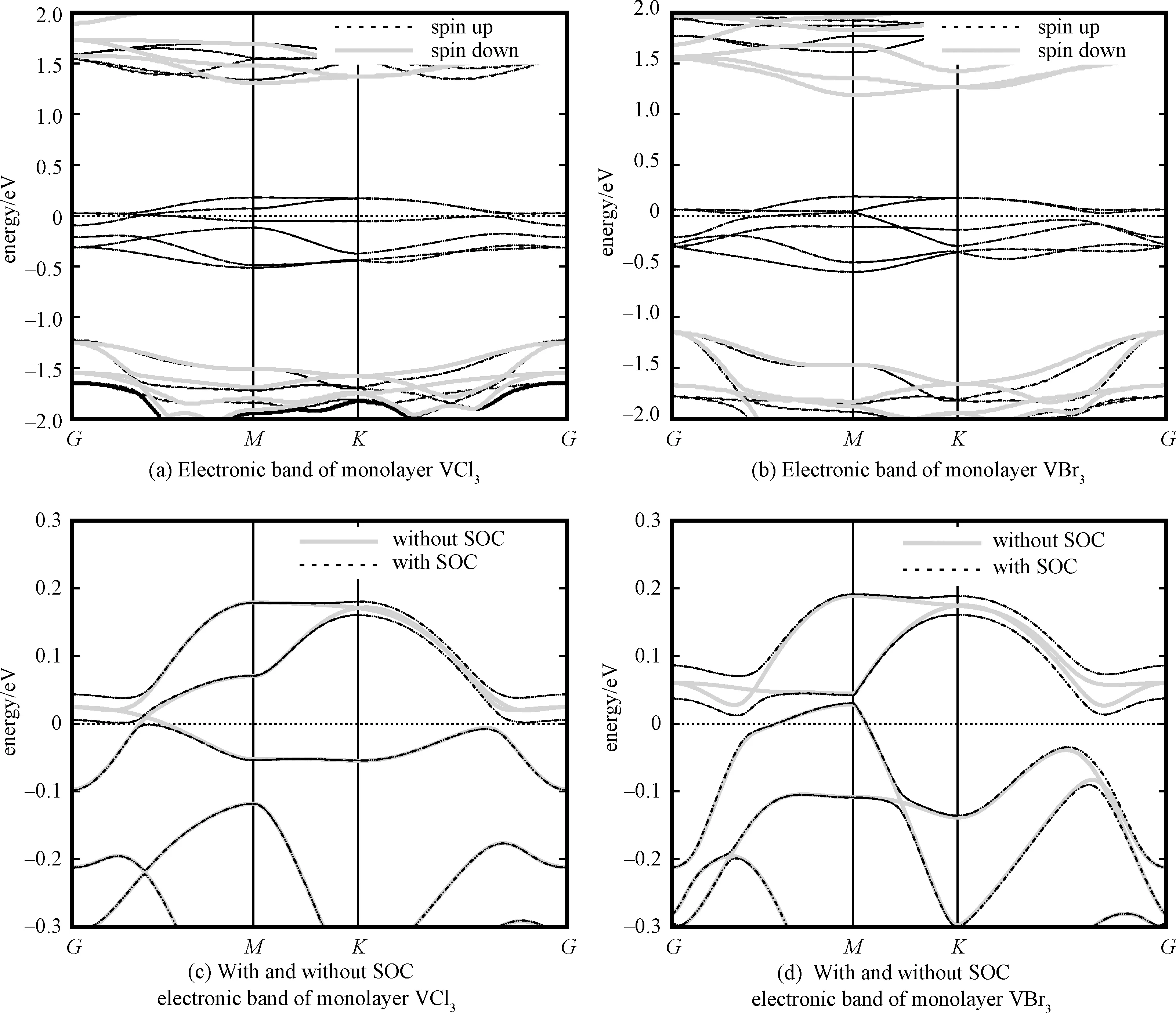
Fig.2 Electronic band structures of monolayer VCl3 and VBr3

Furthermore, because of the ferromagnetic ordering of the magnetic moments in V atoms, the system results in a quantum anomalous Hall insulator. To show the topology, we calculated the gauge-invariant Berry curvature in momentum space. The Berry curvature Ωz(k) in 2D can be obtained by analyzing the Bloch wave functions from the self-consistent potentials

Ωz(k)=∑nfnzΩn(k),

(1)

(2)

wherefnis the Fermi-Dirac distribution function,vx(y)is the velocity operator,ψn(k) is the Bloch wave function,εn(k) is the eigenvalue, the summation is over allnoccupied bands below the Fermi level,mindicates the unoccupied bands above the Fermi level. Based on the first-principle calculations, one observes that, in the absence of SOC, there are totally 6 Weyl nodes (Fig.3(a)) related withC3and inversion symmetry along theG-M(M’) high symmetry lines of the hexagonal Brillouin zone. SOC will open a tiny gap, correspondingly. Six Berry curvature peaks appear. The nonzero Berry curvature mainly distributes around the opened band crossings at the Fermi level. Furthermore, a plot of the 6 Berry curvature peaks over the whole BZ (Fig.3(c)) indicates that all 6 peaks have the same sign. The Chern number can be obtained by integrating the Berry curvature Ωz(k) over the BZ

(3)

Two Berry curvature peaks contribute to the nonzero Chern number 1 and consequently the total Chern number is 3 by integrating the Berry curvature in the whole BZ. According to the bulk-edge correspondence[36], the nonzero Chern number is closely related to the number of nontrivial chiral edge states that emerge inside the bulk gap of a semi-infinite system. With an effective concept of principle layers, an iterative procedure to calculate the Greens function for a semi-infinite system is employed. The momentum and energy dependence of the local density of states at the edge can be obtained from the imaginary part of the surface Greens function and the results are shown in Fig.4(a) and 4(b). It is obvious that there are three gapless chiral edge states that emerge inside the bulk gap connecting the valence and conduction bands corresponding to the Chern numberC=3.

(4)

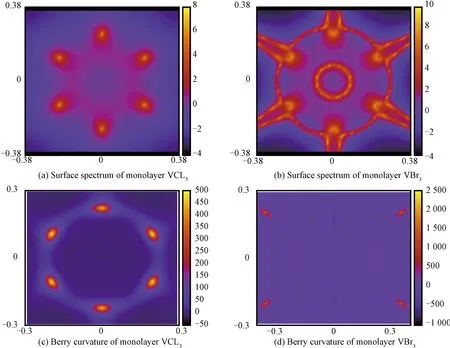
Fig. 3 Surface spectra of monolayer VCl3 at energy level 0.01 eV (a) and monolayer VBr3 at energy level 0.07 eV (b),and Berry curvature of monolayer VCl3 and VBr3 in the BZ (c, d)

As shown in Fig.5 (Fig.6), the change of band structure as a function of correlation strengthUfor monolayer VCl3(VBr3)indicates that there exits a phase transition atU≈0.45 eV (0.35 eV), and stronger correlation will turn it into a Mott insulator. We also calculated the properties of a monolayer VBr3. Although the monolayer VBr3exhibits some similar properties as in VCl3, i.e., a Weyl semimetal without SOC (Fig.2(b)) and an energy gap is opened when including SOC (Fig.2(d)), the monolayer VBr3has the total Chern numberC=1 from 6 Berry curvature peaks, of which 4 peaks have positive sign and 2 peaks have negative sign (Fig.3(d)). The nonzero Chern number 1 corresponds to one gapless chiral edge state (Fig.4(b) and 4(d)) connecting the valence and conduction bands.

3 Discussion

In summary, based on the first-principle calculations, we propose that the 2D monolayer VCl3and VBr3are QAH insulators without considering correlation effect, and they transform into Mott insulators after turning on the correlation effectU. At the mean-field theory level, VCl3and VBr3exhibit QAH insulating states with Chern numbers of 3 and 1, respectively, thus giving rise to chiral gapless edge states. If the correlationUis larger than about 0.45 (0.35) eV for VCl3(VBr3), it will cause a topological phase transition and the monolayer turns into a Mott insulator. These topological properties can be detected by electrical transport experiment, which has been carried out in detecting the QAHE in V-doped (Bi, Sb)2Te3thin film[37], Cr/V-codoped (Bi, Sb)2Te3system[38], and other doped TIs[39].

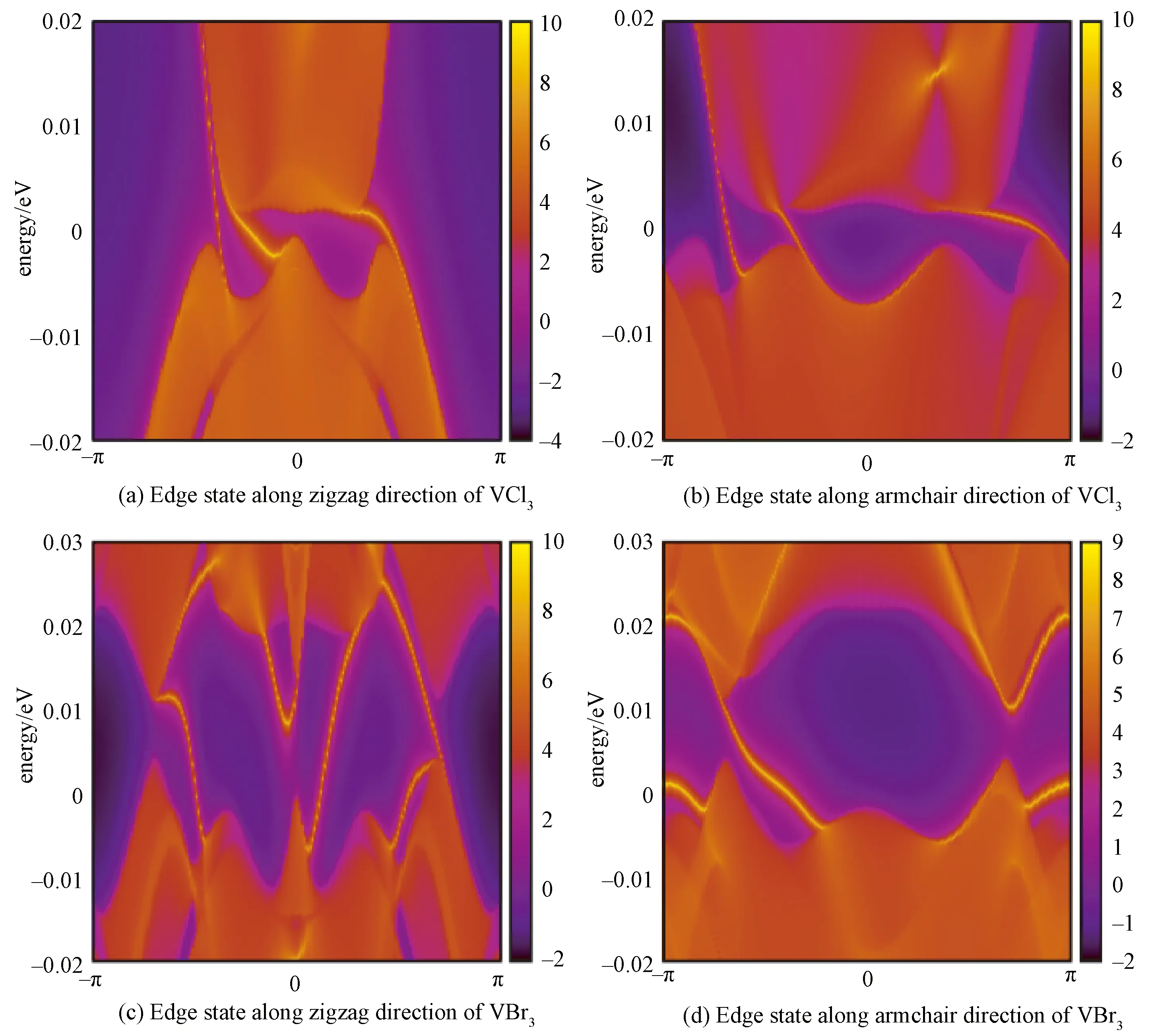
Fig.4 Energy and k-dependence of the local DOS on the edge of the semi-infinite sheet of VCl3 (a, b) and VBr3(c,d)

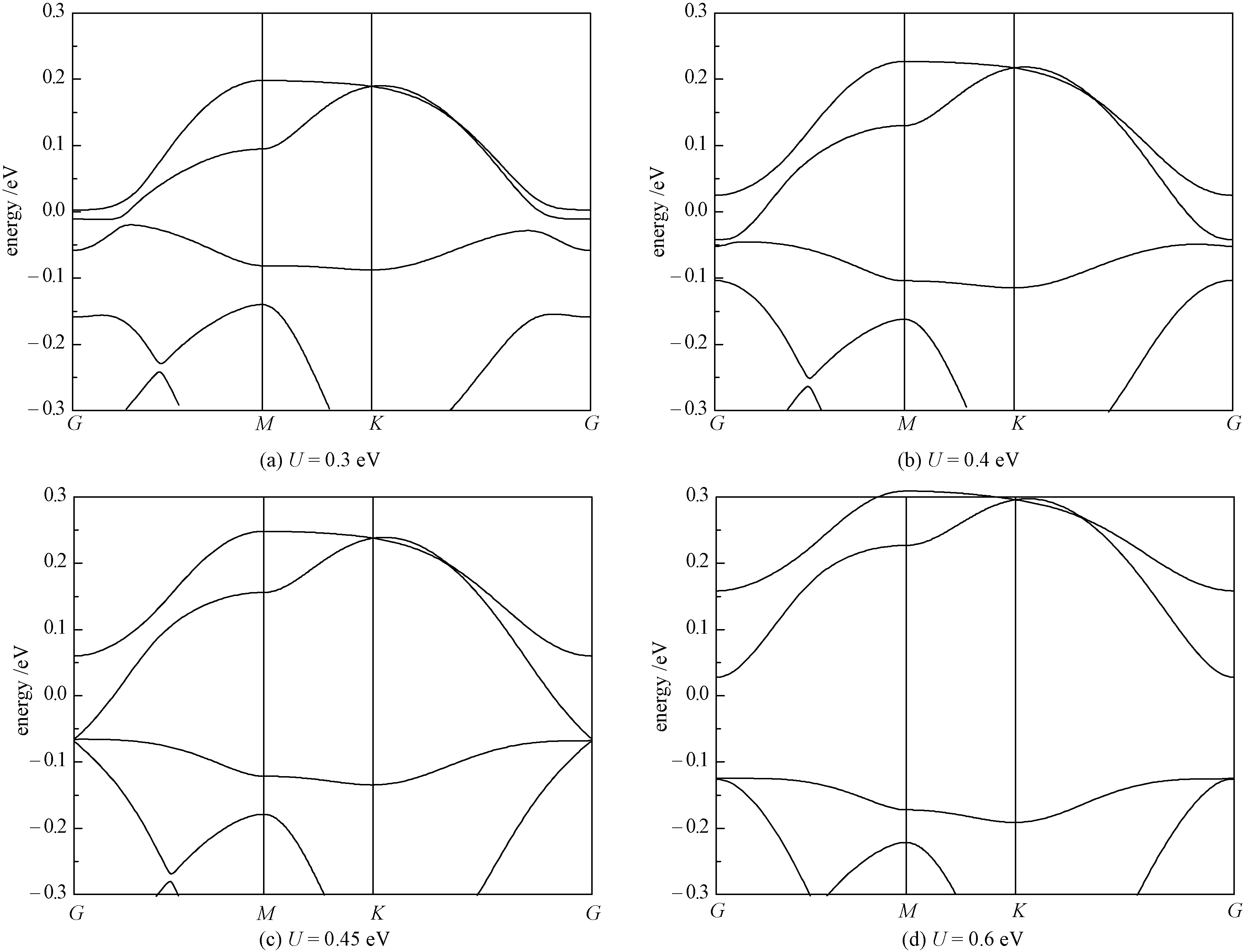
Fig.5 Electronic band structure of monolayer VCl3 with ferromagnetic momentum 4 μB per unit cell along thezigzag direction at different correlation energy values

Fig. 6 Electronic band structure of monolayer VBr3 with ferromagnetic momentum 4 μB per unit cell along thezigzag direction at different correlation energy values

The authors thank YOU Jingyang for helpful discussion.