Conformal minimal immersions of S2 into P4

JIAO Xiaoxiang, CUI Hongbin

(School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China)(Received 3 April 2019； Revised 6 May 2019)

Abstract This work is a generalization of Chen and Jiao’s work, where they considered the question of explicit construction of some conformal minimal two-spheres of constant curvature in quaternionic projective space. The crucial point was to find some horizontal immersions derived from Veronese sequence in P2n+1, which was projected into constant curvature conformal minimal two-spheres by twistor map π:P2n+1→Pn. They calculated the case n=2. In this work, we deal with the case n=4 and a related geometry phenomenon.

Keywords minimal two-sphere; Gaussian curvature; Veronese sequence; quaternionic projective space

In this paper we deal with the caseP4.

In section 1, we review the knowledge of geometry of quaternionic projective space, minimal surfaces in complex projective space, and horizontal equation of immersed surfaces with respect to the twistor map.

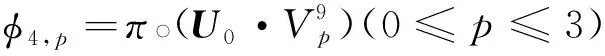
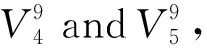
1 Preliminaries

1.1 Geometry of quaternionic projective space

i2=j2=k2=-1,

ij=k=-ji,jk=i=-kj,ki=j=-ik.

(1)

(2)

There is a natural conjugation in, denoted by

(3)

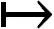
(4)

The quaternionic projective spacePnis the space of-lines inn+1, that is, for [v1]and [v2]∈Pn, [v1]=[v2]if and only if there is anx∈, such thatv2=v1x.

The symplectic group is

Sp(n)={A∈GL(n;)|tA*·A=In},

(5)

whereInis the identity matrix of ordern.

ForA∈Sp(n+1) and [v]∈Pn,Sp(n+1) acts onPnby

A·[v]=[Av].

(6)

G0=Sp(1)×Sp(n)is the isotropy group of this action at[(1,0,…,0)T]and this action is transitive. Therefore,

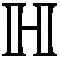
(7)

We have the following commutative diagram

(8)

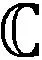
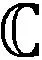
H[v]={w∈v⊥|σv(w)=0,σv=-tz2dz1+tz1dz2}.

(9)

We have the following proposition[10], which is a special case of Lemma 3.5 of Eells and Wood[3].

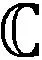
1.2 Minimal surface in a complex projective space

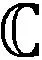
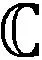
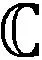
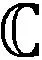
(10)

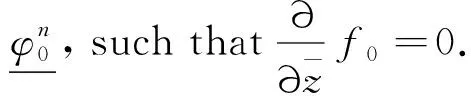
(11)

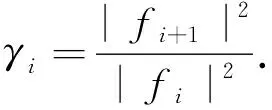
(12)

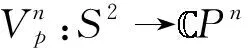
(13)

wherezis a local holomorphic coordinate ofS2,p=0,1,…,n. Forj=0,1,…,n,gp,jare given by

(14)

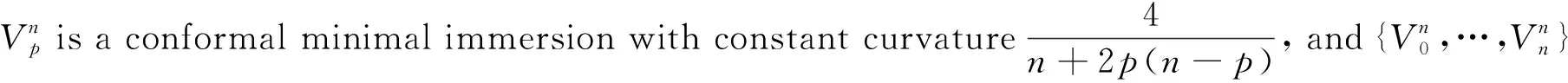
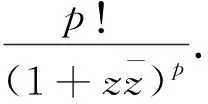
The Veronese sequence is particularly important for the following rigidity theorem[2].

1.3 Horizontal equations of immersed surfaces

Based on the above discussions, we can produce conformal minimal two-spheres from the Veronese two-spheres inPnby a unitary rotation. It is stated in the following proposition[10].

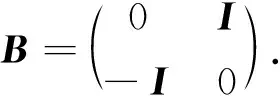
(15)

2 Conformal minimal two-spheres in P4

2.1 Reduced horizontal equation of Veronese maps

Definition2.1LetMbe a Riemann surface, we call two surfacesΨ,Φ:M2→Pnare symplectic equivalent if there is an isometry, i.e., a symplectic matrixH,H·Ψ=Φ.

(16)

(17)

for any integerm.

Proof

g2n+1-p,2n+1-j

(18)

Setk=p+l-j, then we easily see

(19)

Omit (-1)p, then we get the conclusion.

□

(20)

By complex conjugate, we have

(21)

So we only need to consider the casep≤n.

Denotegp,j(0≤p,j≤n) by

(22)

By derivation, we get

(23)

(24)

(25)

for any nonnegative integersm,t.

If we change the positions ofkandlin the second formula (notice thatk+l=t=constant for sometandSij=-Sji), then we get

(26)

Then, usingi+j=m=constant for somemin the first equation, we finally get the equations

(27)

(28)

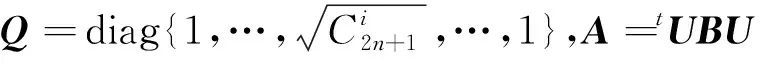
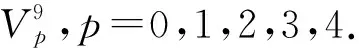
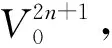
(29)

Notice thatAis an anti-symmetric unitary matrix, soSis anti-symmetric too, the first equation is naturally satisfied, and we can reformulate the second to

(30)

or, write

(31)

It is a linear combination of matrix elements in different lines of upper triangulation part ofS. Now, we talk about the solution in differentn(n≥1).

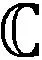
(32)

or, write

(33)

The solution is

(34)

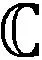
In general, we have

(35)

□

□

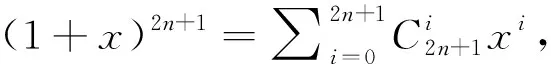
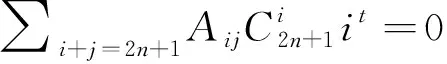
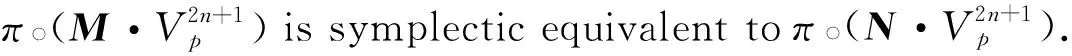
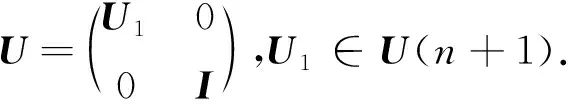
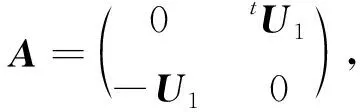
In the rest part of this article, we will always denote the above matrix byU0.

(36)

is also horizontal.

From the above discussion, we have

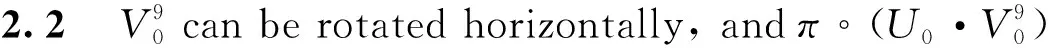
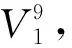
(37)

the second equation of (28) reduce to

(38)

noticeF0=0 is naturally satisfied, then we have

F1=0,F2=0,F3=0.

(39)

The equationsFt=0 whichtis even are degenerate to thosetis odd, since

(40)

and

(41)

by every 0≤t≤2k-1.

So, finally, the equations reduce to

F1=0,F3=0.

(42)

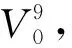
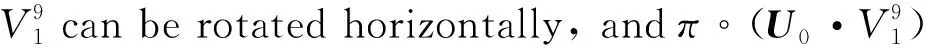
(43)

then we have

F1=0,F2=0,F3=0,F4=0,F5=0.

(44)

So, finally, the equations reduce to

F1=0,F3=0,F5=0.

(45)

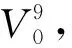
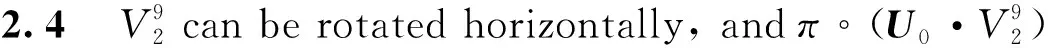
B3*t(F7,F6,F5,F4,F3,F2,F1,F0)=0,

(46)

whereB3 is a 14×8 matrix, it is a big matrix, by using the software Matlab, we calculate rank(B3)=8, so we have

Fi=0

(47)

for 0≤i≤7.

The equationsFt=0 whichtis even are degenerate to thosetis odd.

So, finally, the equations reduce to

F1=0,F3=0,F5=0,F7=0.

(48)

It is still not determinate for the elements of matrixS, so we still have a solutionU=U0, then:

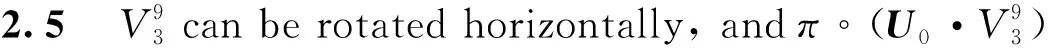
B4*t(F9,F8,F7,F6,F5,F4,F3,F2,F1,F0)=0，

(49)

whereB4 is a 18×10 matrix, we calculate rank(B4)=10, so we have

Fi=0

(50)

for 0≤i≤9.

The equationsFt=0 whichtis even are degenerate to thosetis odd.

So, finally, the equations reduce to

F1=0,F3=0,F5=0,F7=0,F9=0.

(51)

Different like the former cases, this is a over-determined system for the elements of matrixS, since (51) is equivalent to:

(52)

By checking rank of the coefficient matrix of anym,Smust be zero matrix, then

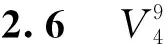
3 The middle terms of harmonic sequence

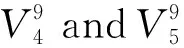
(53)

f4,f5can not be rotated horizontally.

ProofAssumef4can be rotated horizontally,tf4Bdf4=0, from(11),(12),we have

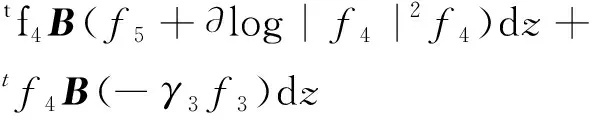
=0,

(54)

SinceBis antisymmetric,tf4Bf4=0, then it is equivalent to

(55)

then we have

(56)

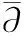
tf0Bfi=0,i=0,1,2,3,4,5,6,7,8,9,

(57)

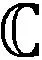
f5is similar, we only need to showf9is a local zero section.

□