结合形状特征及其上下文的多维DTW

王 见，毛黎明，尹爱军

重庆大学 机械工程学院，重庆400044

1 引言

时间序列数据广泛存在于众多应用领域，其相似性分析已受到越来越多的关注。欧式距离和动态时间规整算法（Dynamic Time Warping，DTW）距离是广泛使用的两种相似性度量方法[1]。DTW 能够较好地处理时间序列的偏移、伸缩问题，具有较高的灵活性，在语音识别[2-3]、姿势识别[4-6]、数据挖掘[7-8]、故障识别[9-10]等领域得到广泛研究。DTW 相关的算法主要分为两类：一类以单维时间序列为研究对象；另一类以多维时间序列为研究对象。

对于单维时间序列，Keogh等[11]研究了DDTW（Derivative Dynamic Time Warping）算法，将一阶梯度信息与单维DTW结合，一定程度缓解了传统单维DTW对单维时间序列过度压缩的问题；Górecki 等[12]将一阶梯度信息、二阶梯度信息与单维DTW 结合，进一步提升了单维DTW 的准确性；Zhang 等[13]研究了SC-DTW（Shape Context Dynamic Time Warping）算法，利用上下文信息提高了DTW对单维时间序列相似性分析的准确性。

对于多维时间序列，单维DTW 一般针对其中某一维序列，获取匹配路径，然后将该路径直接作用于其他维序列。然而由单个维度上获得的最优匹配路径不一定是所有维度的最优匹配，一般不使用单维DTW处理多维时间序列。Ten 等[14]研究了多维DTW（Multi-Dimensional DTW，MD-DTW）算法，利用向量记录每个时间点的信息，从而使用所有维度的信息匹配路径，该算法过于简单，忽略了多维时间序列的其他信息。Orsenigo等[15]提出了TDVM（Temporal Discrete SVM）算法，该算法首先利用MD-DTW 将多维时间序列转换成相同的长度，然后使用离散支持向量机对相似性进行度量，计算繁琐，算法复杂度较高。Shen 等[16]将度量学习算法LMNN（Large Margin Nearest Neighbor）与DTW 相结合，使用特定的损失函数来学习马氏矩阵，提高了多维时间序列相似性度量的准确性，但该算法原理复杂，求解困难。Mei 等[17]研究了一种基于马氏矩阵的LDMLDTW，它使用度量学习算法，利用三元约束学习马氏矩阵，取得了较好的度量效果，该算法同样原理复杂，求解困难。

本文借鉴单维DTW的研究成果，将MD-DTW与梯度信息、上下文信息结合，提出了一种综合多维时间序列形状信息及其上下文信息的相似性度量算法（Multi-Dimensional Contextual Dynamic Time Warping，MDCDTW）。该算法首先计算多维时间序列的一阶梯度，然后对其进行采样处理，利用多维时间序列一阶梯度形状信息及其上下文信息来查找最优匹配路径。MDCDTW的原理简单，易于理解和实现。实验结果表明，相较于其他高效算法，MDC-DTW 具有较高的准确率和时间效率。

2 MDC-DTW算法

2.1 DTW算法

DTW是一种通过动态规划寻找时间序列之间最佳匹配路径的算法，能够处理在时间维度上的偏移和伸缩问题。设单维时间序列X 的长度为m,Y 的长度为n，其中X={ x1,x2,…,xm} ，Y={ y1,y2,…,yn} 。构建一个m×n 的距离矩阵D，其中的元素d(i,j)表示xi与yj之间的距离，常用的是欧式距离，d(i,j)=(xi-yj)2。设X与Y 之间的匹配路径为W ，W=w1,w2,…,wk,…,wK,max(m,n)≤K ＜m+n-1，wk=(i,j)表示路径W 中的第k 个元素为xi映射到yj。为了保证匹配的有效性，W需满足下面三个约束条件：

（1）边界条件：w1=(1,1)，wK=(m,n)。

（2）连续型：设wk=(p,q) ，wk+1=(p′,q′) ，需满足p′-p ≤1 和q′-q ≤1。

（3）单调性：设wk=(p,q) ，wk+1=(p′,q′) ，需满足p′-p ≥0 和q′-q ≥0。

可能存在多个W 满足以上三个条件，DTW通过动态规划寻找其中距离最短的路径。设s(i,j)表示距离矩阵D 中(1,1)到(i,j)的路径长度，最短路径的求解如式（1）所示：

2.2 结合形状特征及其上下文的多维DTW

MDC-DTW 的设计借鉴了单维DTW 的研究成果，本文与MDC-DTW 设计相关的几个算法之间的关系如图1 所示。传统DTW 进行多维时间序列相似性分析时，只利用了单个维度的信息，丢失了其他维度的信息；MD-DTW 同样存在着缺陷，它虽然考虑了所有维度的坐标信息，但是进行时间序列相似性匹配计算时，可能形状的信息更加重要；MDe-DTW（Multidimensional Derivative Dynamic Time Warping）将梯度形状信息与MD-DTW结合，然而这种算法仍然存在不足，它只考虑单个点的形状信息而忽略了上下文信息；MDC-DTW将梯度形状信息和上下文信息与MD-DTW 结合，利用的信息更加全面。

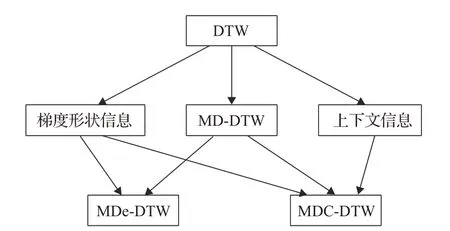
图1 各算法之间的关系图

A 和B 是两个K 维的多维时间序列，它们的长度分别为M 和N ，利用式（2）计算多维时间序列的一阶梯度：

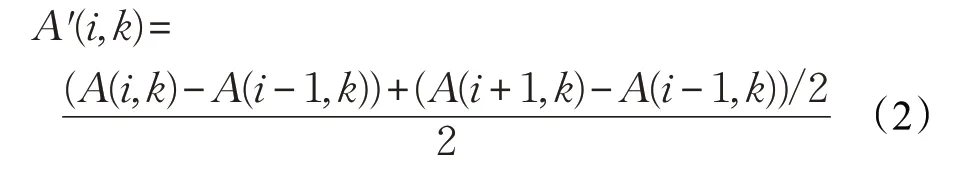
对时间序列进行采样，获取上下文描述因子。设U(i,k)为对A′(i,k)进行采样后的上下文描述因子，采样长度为L=5，U(i,k)的计算如式（3）所示：

MDC-DTW的d(i,j)计算如式（4）所示：

MDC-DTW的原理示意图如图2所示。

图2 MDC-DTW的原理示意图

3 对比实验

3.1 仿真数据

随机产生二维时间序列，并通过缩放、拉伸得到变形之后的时间序列，如图3（a）所示。左侧是维度1，右侧是维度2，红色曲线为原始时间序列，黑色曲线为经过缩放、伸缩之后的时间序列，中间蓝色虚线为匹配路径。传统DTW 利用维度1 数据获得匹配路径，并将该匹配路径应用于维度2，结果如图3（b）所示；MD-DTW 利用了所有维度的信息，结果如图3（c）所示；MDe-DTW 利用所有维度的一阶梯度形状信息，结果如图3（d）所示；MDC-DTW 利用了所有维度的一阶梯度形状及其上下文信息，结果如图3（e）所示。

图3 仿真数据运行结果

将各个算法的运行结果与真实的匹配路径进行对比，DTW和MD-DTW的运行结果中存在过多一点映射多点的匹配，对时间序列造成过度压缩；MDe-DTW 运行结果的前半部分和真实匹配相距较大，后半部分和真实匹配较接近；MDC-DTW的运行结果和真实匹配很接近，相较于另外3个算法，MDC-DTW的性能更优异。

根据算法原理对结果进行分析，传统DTW 丢失了维度2 的信息；MD-DTW 虽然利用了所有维度的信息，但只利用了数据点的y 轴坐标信息；MDe-DTW利用了所有维度的一阶梯度形状信息，在该仿真数据上，使用一阶梯度形状信息相较于使用y 轴坐标信息准确性更高；MDC-DTW利用了一阶梯度形状信息及其上下文信息，考虑更加全面，得到的匹配结果也更加准确。

3.2 多维时间序列分类实验I

从UEA Time Series Classification Repository中选出9 个多维时间序列数据集，各个数据集的信息如表1所示。DTW、MD-DTW、MDe-DTW以及MDC-DTW都是度量距离的算法，因此需要结合1-NN 算法来进行分类实验，最后通过比较分类的正确率来比较各算法的准确性。实验中采用了五折交叉验证（Cross-Validation）方法，取平均值作为分类的准确率。在MDC-DTW 中，比较了3个不同采样长度（5、10、15）下的准确率。各个算法的简要描述如表2所示，实验得到的分类正确率如表3所示。

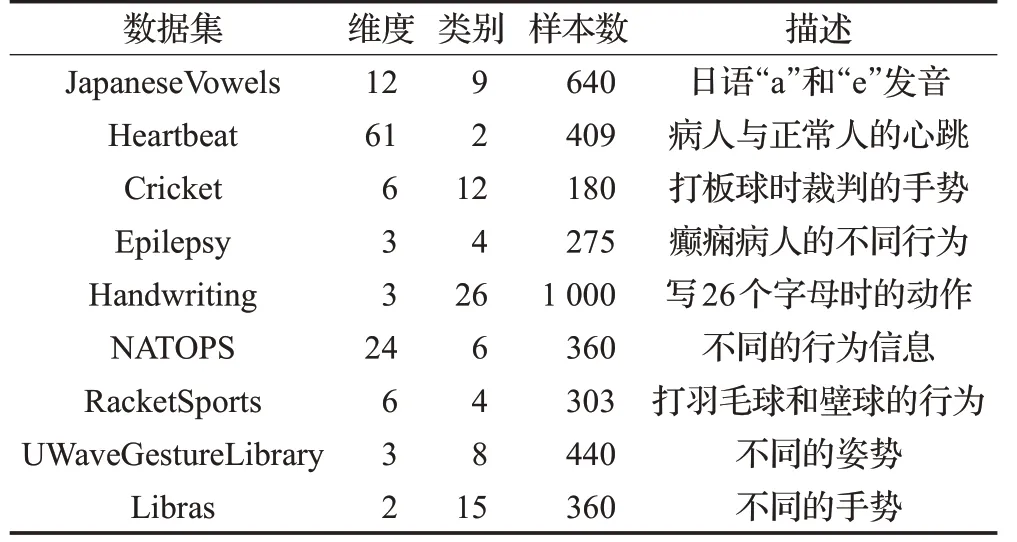
表1 数据集信息I

表2 各个算法的简要描述

从表3可以看出，采样长度对MDC-DTW的评价效果有不同程度的影响，但是MDC-DTW的准确率都要比其他3 个算法的准确率高。从算法的原理上理解，MDC-DTW在进行时间点匹配时，使用了时间点的形状信息及其上下文信息，使用的信息更加全面，匹配更加准确。综合来看，本文提出的MDC-DTW算法在上述9个多维时间序列集上的效果要比DTW、MD-DTW 和MDe-DTW 的效果好。结合上述实验结果可知，MDCDTW算法的设计是合理的。

3.3 多维时间序列分类实验II

为进一步检测MDC-DTW 的性能，将MDC-DTW与LDML-DTW[17]、LMNN-DTW[16]、TDVM[15]和LBM[18]等高级算法进行比较。实验中采用了五折交叉验证方法，取平均值作为分类的准确率，MDC-DTW 的采样长度设置为5。实验中选取了5 个数据集，它们的信息如表4所示，实验结果如表5所示。

由表5 可知，在JapaneseVowels、PenDigits、LP1 和LP4 这4 个数据集上，MDC-DTW 的分类准确率略低于LDML-DTW；但在其余数据集上，MDC-DTW的表现明显优于LDML-DTW、LMNN-DTW、TDVM、LBM，这表明MDC-DTW有着较高的准确性。

3.4 算法复杂度分析

将MDC-DTW算法与当前表现较好的LDML-DTW算法进行时间复杂度的对比分析，MDC-DTW算法的时间复杂度是O(Nldmn)，LDML-DTW 算法的时间复杂度是O(Nd2mn)，其中N 为训练样本的个数，l 为采样长度，d 为样本维度，m 和n 为样本的长度。设置MDCDTW的采样长度l=5。在5个数据集上，两种算法的运行时间如图4 所示。由图4（a）可知，在JapaneseVowels数据集上，MDC-DTW 相较于LDML-DTW 用时更少；在Libras、PenDigits 和Character Trajectories 数据集上，MDC-DTW 相较于LDML-DTW 用时更多。由图4（b）可知，在LP数据集上，MDC-DTW相较于LDML-DTW普遍用时更少。这主要是因为Libras、PenDigits和Character Trajectories数据集的维度小于MDC-DTW的采样长度，而JapaneseVowels 和LP 数据集的维度大于MDC-DTW的采样长度。

表3 多维时间序列分类实验的正确率I

表4 数据集信息II

表5 多维时间序列分类实验的正确率II

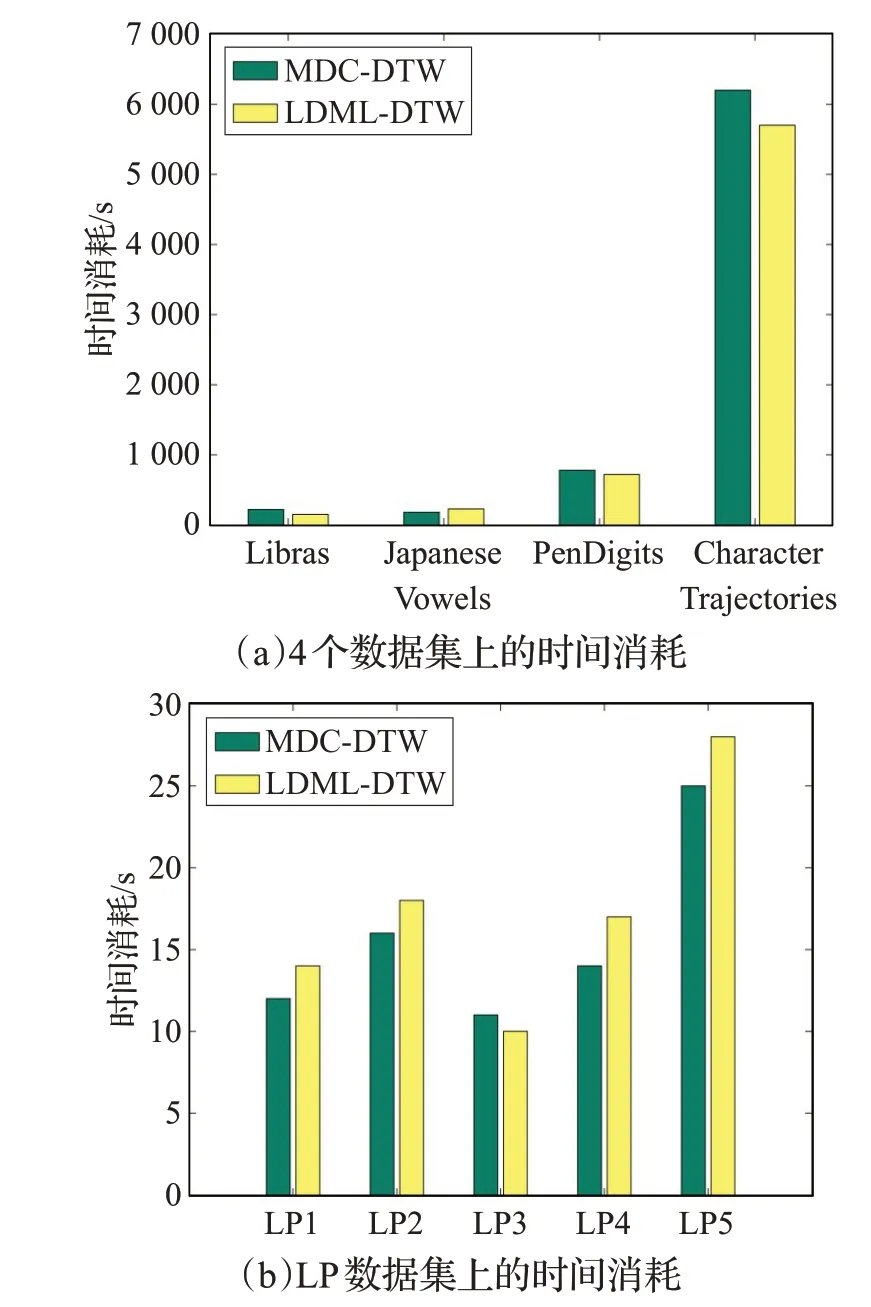
图4 分类时间消耗

4 结束语

本文针对多维时间序列的相似性分析提出了一种结合形状特征及其上下文的MDC-DTW算法，并对该算法进行了两方面的研究：一是研究了MDC-DTW算法设计的合理性；二是研究了MDC-DTW算法的性能。在算法设计合理性方面，对该算法从定性分析和定量分析的角度分别进行了探究。与MDC-DTW 设计相关的有DTW、MD-DTW、MDe-DTW 算法。在定性分析上，本文使用二维的时间序列数据，对其进行缩放、拉伸处理，获得仿真的二维时间序列数据，然后利用DTW、MDDTW、MDe-DTW、MDC-DTW 获取仿真时间序列数据和真实时间序列数据之间的匹配路径，可视化展示算法的运行结果，并将其和真实的匹配进行对比，直观展示出MDC-DTW 算法相比其余3 个算法准确性更高。在定量分析上，本文使用了9 个多维时间序列数据集，将DTW、MD-DTW、MDe-DTW、MDC-DTW 与1-NN 算法结合进行分类实验，获取分类正确率，通过分类正确率来评估各算法在多维时间序列相似性分析上的准确性。实验结果表明，相比另外3 个算法，MDC-DTW 具有一定的优越性，MDC-DTW的设计是合理的。在算法性能方面，本文对MDC-DTW算法的准确率和时间效率进行了研究。在准确率研究上，利用5个多维时间序列数据集，结合1-NN 算法，对MDC-DTW 算法与当前表现优异的4个多维DTW算法进行了分类实验对比。实验结果表明，相较于这4 个高效算法，MDC-DTW 有着较高的准确率。在时间复杂度研究上，将MDC-DTW和当前表现较好的LDML-DTW算法进行对比分析，实验结果表明，当采样长度小于数据维度时，MDC-DTW 的耗时相对更少；当采样长度大于数据维度时，MDCDTW稍慢于LDML-DTW。