具有加权特性的弹性网络聚类算法研究

衣俊艳，吴博雅，雍巧玲

1.北京建筑大学 电气与信息工程学院，北京100044

2.喀什大学 计算机科学与技术学院，新疆 喀什844000

1 引言

聚类是目前处理数据的重要手段之一，已广泛应用于诸如生物学[1-2]、图像处理[3]、金融分析[4-5]等学科领域。聚类是根据一组定义，将一组对象划分为多个集群的过程，其目的是使同一集群中的对象比不同集群中的对象彼此间更加相似[6]。与监督学习相比，聚类算法通常属于无监督学习范畴，这也增加了数据聚类的难度。聚类分析技术不仅可以挖掘数据之间的内在联系，揭示数据的分布特性，还可以作为数据的一种预处理方式，便于后续的数据分析任务[7]。

传统的聚类算法可以分为五类：基于划分的聚类、基于网格的聚类、基于层次的聚类、基于密度的聚类、基于模型的聚类。近年来出现了很多新的聚类算法，如基于粒度的聚类算法、基于熵的聚类算法、不确定聚类算法、谱聚类算法、核聚类算法等[8-9]。虽然目前已经有很多关于聚类的算法，但这些算法仍存在以下缺点：可伸缩性差；容易受到噪声点、离群值等因素的影响；无法自动确定簇数；无法聚类非线性可分离数据集；多维空间聚类质量变差等[10]。

基于划分的聚类算法如k-means、k-medoids等，其中k-means算法[11-13]具有简单、高效等优点，但其由于对噪声点及数据输入顺序的敏感性导致算法结果不稳定的问题是不容忽视的。k-medoids[14]虽然针对该问题进行了改进，但仍未彻底解决。此外，基于划分的聚类算法大多不能很好地处理具有非凸特性的数据集。基于网格的聚类算法如STING（STatistical INformation Gridbased method）[15]、CLIQUE（Clustering in Quest）[16]等，擅长解决高维大型的数据集，但其求解质量有待提高。基于层次的聚类算法如CURE[17]，能以较低的时间复杂度解决大型数据集，但也存在聚类结果不稳定、聚类质量不高等问题。基于密度的聚类算法如DBSCAN（Density-Based Spatial Clustering of Applications with Noise）[18]、MeanShift[19]等，可以发现数据集中任意形状的集群，可以排除噪声的干扰，但不能很好地解决高维问题。基于模型的聚类算法如COBWEB、SOM 等，其中典型的统计学方法COBWEB[20]的算法简单，能够快速处理数量级大的数据集，但无法很好地处理多维数据集。典型的神经网络方法SOM（Self-Organizing Map）[21]，能够很好地处理高维数据，不受噪声点的影响，但该算法存在不能保证网络全局收敛等问题。

由SOM网络延伸出来的弹性网络算法（Elastic Net Method）在1987 年被Durbin 和Willshaw 提出[22]，该方法提出伊始被用来解决具有NPC计算复杂性的旅行商问题（Traveling Salesman Problem，TSP）。在没有先验知识的条件下进行聚类，一种有效的方法是设定一个聚类的目标函数，求解该函数的最小值，从而获得具有最佳分布函数的聚类方案。弹性网络非常适合求解这类问题，可以针对目标函数自动求解，不需要其他人工指导训练，且保证网络系统全局收敛。

熵最初是物理学中对系统混乱程度的一种度量，后有科学家从数学角度提出信息熵的概念。1957 年统计物理学家Jaynes提出极大熵原理后，该原理被广泛应用于许多学科领域中。该原理认为，在掌握部分信息的情况下对分布形状做出判断，应该选择符合约束条件且熵值取得最大的概率分布，任何其他的选择都意味着人为添加了其他的约束条件，而这些约束或假设是无法根据现有的知识给出的。此外，Jaynes 还指出，在物理学中一些重要的概率分布均是在一定约束条件下满足极大熵原理的概率分布[23-24]。更为重要的是，极大熵原理满足第一原理和一致性要求，即极大熵原理利用最少的信息，获得最超然（Maximally Noncommittal）的解，并且求得的解与求解步骤无关[25-26]。

本文结合极大熵原理、模拟退火思想[27]，应用弹性网络的求解模式，提出一种新的聚类算法。该算法重新构造与数据点、聚类中心关联的代价函数，并考虑了各特征属性对聚类不同程度的重要性等因素，提出一种具有加权特性的弹性网络聚类算法（Weighting of Elastic Net for Clustering，WENC）。

2 弹性网络

弹性网络算法的基本原理是在多元空间中描述各城市点，在城市点构成的空间内生成一个含有弹性节点（Elastic Points）的以数据集重心为中心的封闭圆环，该圆环称为弹性带（Rubber Band）。随着网络不断地迭代，弹性带发生形变，弹性节点的位置不断变化，不断向城市点靠近，直到所有的城市点被弹性节点覆盖，网络达到稳定状态，即认为获得该TSP问题的近似解。在迭代过程中，弹性网络通过两种力来牵引弹性节点的移动：一种力是与弹性节点i 相邻的城市点对弹性节点i的吸引力，使得弹性节点i 逐渐向城市点靠近；一种力是与弹性节点i 相邻的弹性节点对弹性节点i 的张力，迫使弹性节点之间的距离最短。

假设给定数据集X={x1,x2,…,xn} 含有n 个城市点，在该空间内初始化含有m 个弹性节点的弹性带Y={y1,y2,…,ym}，一般n ＜m 。随着网络的迭代，弹性网络追踪能量函数式（1）的极小值：

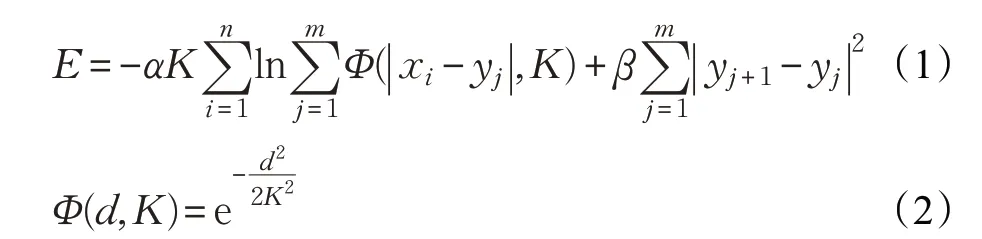
其中，K 逐渐减小，与退火算法（Deterministic Annealing Method）中的温度对应。参数α、β 分别决定城市对弹性节点的力和弹性点间的力的影响程度。弹性节点每次迭代需要的位移量为：

其中，ωij代表城市点i 在路径上对弹性节点j 的影响程度，其描述如式（4）所示。

当K →0 时，能量函数获得局部最小，此时每个城市点至少匹配到一个弹性节点。当城市点有且只匹配到一个弹性节点时，认为网络获得最优解决方案。

3 具有加权特性的弹性网络聚类算法

传统的聚类分析算法通常将数据所有的特征属性按照相同的重要程度进行聚类，然而在多维数据聚类中，所有的特征属性对聚类的重要程度并不完全相同，有些特征属性甚至可能是噪声特征，进而影响聚类的结果[7，28]。本文根据弹性网络的特点，设计了一种加权方式，使其能够在多维数据集中更好地进行聚类。弹性网络算法虽然非常适合求解具有目标函数的问题，但并不能直接用于解决聚类问题，本文将详细介绍具有加权特性的弹性网络聚类算法。首先，根据聚类的目标确定初始权值的方法。然后，引入加权思想，针对聚类问题构建基于数据点与聚类中心间距离平方的能量函数，并运用极大熵原理给出数据点的概率分布。然后，针对算法的弹性带初始化、能量函数、权值等问题进行详细分析。最后，给出算法的执行过程。

3.1 算法原理及分析

假设在多元空间中，给定一含有n 个数据点的数据集X={X1,X2,…,Xn}，每个数据点均具有m 个特征属性Xi=(xi,1,xi,2,…,xi,m)，目标是将该数据集分为k 簇。初始化一条含有k 个弹性节点的弹性带Y={Y1,Y2,…,Ym}，每个弹性节点均具有m 个特征属性Yj=(yj,1,yj,2,…,yj,m)，每个特征属性上所加的权值为U=(u1,u2,…,um)。考虑到各特征属性在聚类过程中的影响各不相同，因此需要确定各特征属性的权值。本文首先介绍一种确定特征属性权值的方法。

在弹性网络聚类算法（Elastic Net for Clustering，ENC）中，所有特征属性对聚类过程的影响程度相同，此时相当于各特征属性的权值均为1，即U=(u1,u2,…,um)=(1,1,…,1)，相当于网络不加权。如果某一维对聚类的影响度不那么重要，其存在甚至影响聚类结果变差，但若直接删掉该特征属性，会破坏数据集原本的结构。因此需要对该特征属性的权值进行处理，一方面减少其对聚类结果的影响，另一方面保留了原始数据集的结构特性。

聚类的目的是根据数据的内部结构，将数据划分成一些集群，每个集群中的对象尽可能相同，不同集群中的对象尽可能不同，由此可以判定，当某特征属性较为离散时，该特征属性不利于聚类。本文首先利用式（5）对所有特征属性的离散程度进行判断，其中xˉl为第l 个特征属性的所有数据点的均值。然后根据式（6）计算阈值：当某特征属性的离散程度超过该阈值时，根据式（7）计算该特征属性的权值，其中δ 为权值系数，根据数据集的特征选取；当某特征属性的离散程度未超过该阈值时，该特征属性的权值为1。

聚类的目标是使类内对象尽可能相似而类间对象尽可能不同，即数据点到各簇中心的距离和最小，根据该目标可以发现衡量聚类质量的一个重要标准SED（Sum of Euclidean Distance）值与此概念一致，如式（8）所示：

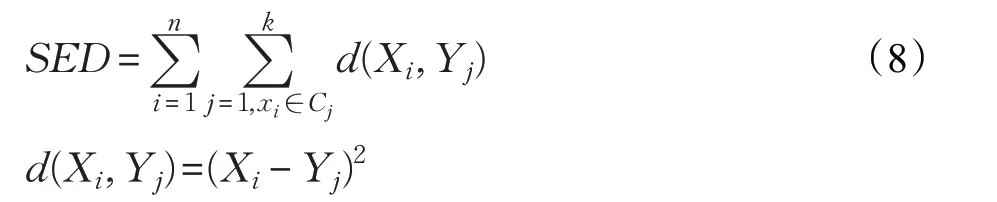
其中，Xi为第i 个数据点，Yj为第j 个聚类中心点，Cj表示聚类产生的以Yj为聚类中心的集群。

本文针对聚类问题，直接将各簇之间的距离平方和设置为能量函数，如式（9）所示。在该能量函数的作用下，所有数据点对每个神经元都具有吸引力，神经元在该力的作用下进行移动。随着网络的运行，能量函数值不断下降，神经元沿着使SED值最小的方向移动，当能量函数达到全局极小，SED 值也达到最小值，从而求得该聚类问题的最优解或近似最优解。此外，传统的聚类分析算法通常将数据所有的特征属性按照相同的重要程度进行聚类，然而在多维数据聚类中，所有的特征属性对聚类的重要程度并不完全相同，有些特征属性甚至可能是噪声特征，进而影响聚类的结果。因此，本文引入加权思想，将能量函数定义为式（9），总的能量函数定义为式（10）。

其中，Pi,j为数据点xi属于某一簇Cj的概率分布，在没有先验知识的情况下，不能随便确定其具体模式。本文采用极大熵原理来确定Pi,j的概率分布。

将聚类模型视作物理系统模型，对给定的弹性节点y1,y2,…,yk定义熵函数H ，如式（11）所示。

在本文的能量函数中，除考虑数据点与弹性节点之间的作用外，还考虑了弹性节点之间的交互作用，如式（12）所示。

其中，常数λ 为弹性系数。

综上，与能量函数相应的亥姆霍兹自由能（Helmholtz Free Energy）如式（13）所示[29-30]，其中Z 为总的配分方程。

本文将数据集中的数据点描述为多变量空间中的数据点，在没有先验知识，也不对数据集做任何假设约束的情况下，利用极大熵原理来确定弹性节点与数据点之间的概率分布。在该算法中弹性网络节点的位置代表聚类中心，而每个数据点隶属于该簇的概率符合高斯概率分布，由式（14）给出[26，29]。

其中，Zi为配分方程：

其中，参数β 与温度K 成反比，即β 越小温度越高，当β=0 时，每个数据点属于每簇的概率相同；随着β 不断增加，当β →∞时，每个数据点以1 的概率仅属于一个簇。由于每个数据点属于不同簇的概率是不同的，因而总的配分方程为：

在网络不断迭代的过程中，弹性节点在数据点的吸引力和相邻弹性节点间的张力的作用下不断移动位置，每次迭代需要移动的量由式（17）计算得到：

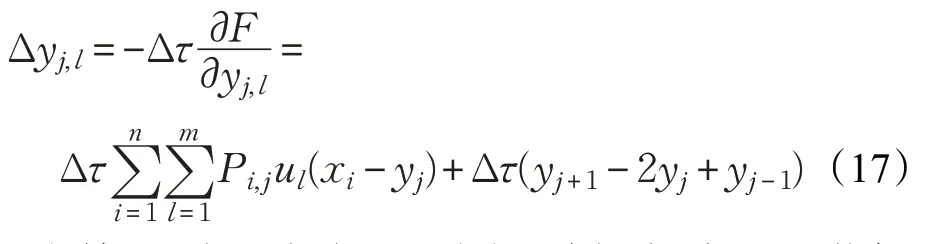
其中，常数Δτ 为每次迭代的步长，选择合适的Δτ 能够使网络进行充分的运行。

3.1.1 弹性带初始化算法分析

由于k-means、k-medoids 算法随机确定初始的聚类中心点，每次运算的结果受到聚类中心点初始位置的影响，使得算法针对同一问题每次运算的结果不唯一。而本文提出的WENC 算法通过设置弹性带的方式，对神经元位置进行初始化，使算法针对同一问题求解结果唯一。WENC算法初始化弹性带的方法描述如下：

其中，xi,l表示第i 个数据点的第l 个特征属性。

（2）利用式（19）计算初始弹性带的半径R：

（3）初始化弹性带为以重心Xˉ为圆心，以R 为半径的封闭圆环，在本算法中选择前两维初始弹性带，k 个弹性节点均匀分布在弹性带上。

该方法综合考虑了所有数据样本的位置，根据所有数据点的坐标计算该数据集的重心Xˉ，继而确定神经元的初始位置。该方法可以根据不同的数据分布情况动态调节弹性网络神经元的初始位置，以适应不同问题的需要。在使用该方法确定弹性网络初始神经元位置后，针对同一聚类问题，WENC网络运行结果唯一。

为验证WENC算法与k-means、k-medoids算法聚类结果的稳定性，本文做了大量实验，此处选取含有800、1 000、3 000、5 000 个数据点的4 组数据集，分别利用k-means、k-medoids、WENC 算法多次运行，结果对比如图1所示。

从图1 中可以发现，针对同一问题，k -means、k -medoids算法多次运行结果不唯一，而WENC 算法多次运行的结果唯一。在20 次的运行中，WENC 算法的结果均优于k-means、k-medoids算法。在这4组实验中，WENC 算法求解的SED 值分别比k -means 算法求解的SED 平均值减少5.22%、5.26%、3.83%、5.00%，比k -medoids 算法求解的SED 平均值减少6.55%、5.15%、8.25%、6.15%。因此在本文后续实验中，利用k-means、k-medoids算法对每组数据集分别进行20次测试，取结果的平均值进行比较。

3.1.2 能量函数分析

为评估WENC 算法自由能函数的作用，本文选取一组含有1 000个数据点的数据集来展示在聚类过程中自由能函数及其对应的SED 值随迭代的演化过程，如图2 所示。图2（a）为WENC 算法的自由能函数随迭代的变化过程，图2（b）为在聚类过程中，每次迭代自由能函数变化时对应的SED值。由图2可知，随着迭代次数的增加，自由能函数值逐渐降低，对应的SED值逐渐减少。在此过程中，网络会陷入局部极小值，因此自由能函数值与SED 值均出现一个较为稳定的状态。随着迭代继续进行，在能量函数的作用下，网络具有针对该聚类问题的自适应、自学习能力，从而能够主动跳出局部极小，寻找到更接近全局最小的解。

图1 k-means、k-medoids、WENC算法多次运行结果对比图

图2 WENC算法自由能函数及对应SED值随迭代的演化图

本文所提出的能量函数，除考虑了数据点与弹性节点之间的作用外，还考虑了弹性节点之间的交互作用：在能量函数中增加了式（12），即增加了相邻神经元之间的吸引力。这有助于保持网络拓扑结构，保证网络运行和求解的稳定性。通常情况下，由于弹性网络神经元节点数目等于聚类数目，大量数据点与少量弹性节点交互，因此能量函数中有关相邻神经元相互作用的计算量增量有限。为验证考虑弹性节点间作用力对网络运算的影响，本文选取一组含有500 个数据点的数据集，分别使用未考虑弹性节点间影响力的NENC（Non-node Elastic Net of Clustering）算法和本文提出的考虑弹性节点间影响力的WENC算法迭代100次，SED值随迭代的变化以及运行所用的时间对比如图3所示。从图3可以发现：在聚类结果上，WENC 算法和NENC 算法每次迭代在SED值上的差别并不明显；在运行时间上，两种算法均迭代100次，WENC算法比NENC算法运行时间仅多了0.02 s。可见弹性节点之间的交互作用对算法运算的成本影响较小，因此在计算成本方面神经元之间的交互作用可以视为扰动。

图3 WENC、NENC算法的SED值变化及运行时间对比图

相邻神经元之间的相互作用，在网络的运行求解过程中起到重要作用，它有助于保持网络的拓扑结构，并保证网络求解的稳定性和唯一性。图4 为针对同一四维含有1 000 个数据点的聚类问题，多次运行WENC算法和NENC 算法的结果对比。由图4 可见，未添加弹性节点之间相互作用的NENC 算法每次运行的结果不稳定，而WENC 算法则在多次计算中取得稳定的唯一解。因此，考虑相邻神经元间的相互作用是非常必要的。

图4 WENC算法与NENC算法多次运行的结果对比图

通过上述理论分析和实验验证，本文提出的WENC算法在能量函数公式（13）的作用下，网络中的每一个弹性节点yj在数据点的吸引力和相邻弹性节点间的张力作用下不断移动位置。如图5 所示为某时刻单个弹性节点yj与数据点xi之间的力的作用图，F1为相邻弹性节点对弹性节点yj的张力之和，F2为数据点xi对弹性节点yj的吸引力。

图5 某时刻单个神经元的受力图

在神经网络中，一般通过观察单神经元模型来验证神经网络的性能及改进方法对网络的影响。但由于弹性网络中弹性节点是在相邻弹性节点和数据点共同作用下进行移动，因此通过单神经元模型进行观察的方法并不适用于弹性网络。本文选取只含有3 个神经元的简单网络模型进行实验，通过选取单个典型神经元作为观察点来验证加权后对速度的影响。单个弹性节点每次迭代移动的量随着迭代次数的增加逐渐趋于0，当弹性节点的移动量连续10 次小于0.001 时，网络停止运行，此时弹性节点的位置即为聚类中心点的位置。

基于以上理论分析，本文对网络迭代速度进行了实验，得到如图6所示结果。图6（a）、（b）分别为弹性节点横纵坐标每次迭代的位移量的变化过程，其中WENC为本文提出的加权弹性网络聚类算法，ENC为未进行加权的弹性网络聚类算法。从图6可以看出，本文提出的WENC 算法迭代了26 次即得到聚类结果，运行时间为0.528 s；ENC 算法则迭代了28 次，运行时间为0.544 s。此外，本文在不同数据集下还进行了网络聚类所需迭代次数的对比，结果如图7所示。从图7可以发现，在不同大小的数据集下，WENC 算法的迭代次数均少于ENC算法。因此，改进后的加权弹性网络WENC 能够更快地找到聚类中心，比不加权的ENC算法的性能更高。

图6 弹性节点横纵坐标位移量的变化过程

图7 不同大小数据集的迭代次数对比图

3.1.3 权值设置分析

为验证加权对网络的影响和意义，本文选取一组随机数据集将WENC算法与其他常用聚类算法进行实验比对。该数据集共含有3 个特征属性，180 个样本点。在本实验中，利用SED 值对聚类的结果进行评价，SED值越小，代表聚类的质量越高。

首先根据式（5）分别计算各特征属性的离散程度，结果如表1所示。然后利用式（6）计算得阈值V=3.40，由此判断仅第3个特征属性需要计算新的权值，其余特征属性权值仍为1。

表1 三维随机数据集所有特征属性的离散程度

根据该数据集的结构，设置参数δ 为0.96，计算得第3 个特征属性的权值为0.5，本文提出的WENC算法与不加权弹性网络ENC、k -means、k -medoids、MeanShift 聚类算法的结果对比如表2 所示。其中，k -means、k -medoids 算法对初始中心点的位置非常敏感。每种算法分别进行20 次测试，取所有SED 值的平均值作为最终结果进行比较。

表2 三维180个样本点的数据集各聚类算法结果对比

由表2的数据对比可知，对数据集进行加权之后网络聚类效果更好，与k-means、k-medoids、MeanShift以及不加权的ENC 算法相比，SED 值分别提高8.5%、6.6%、11.4%、4.1%。 k -means、k -medoids、MeanShift、ENC以及WENC各算法结果的平面图分别如图8～图12所示，其中图（a）、（b）、（c）分别显示了数据集中各属性维度之间的关系。

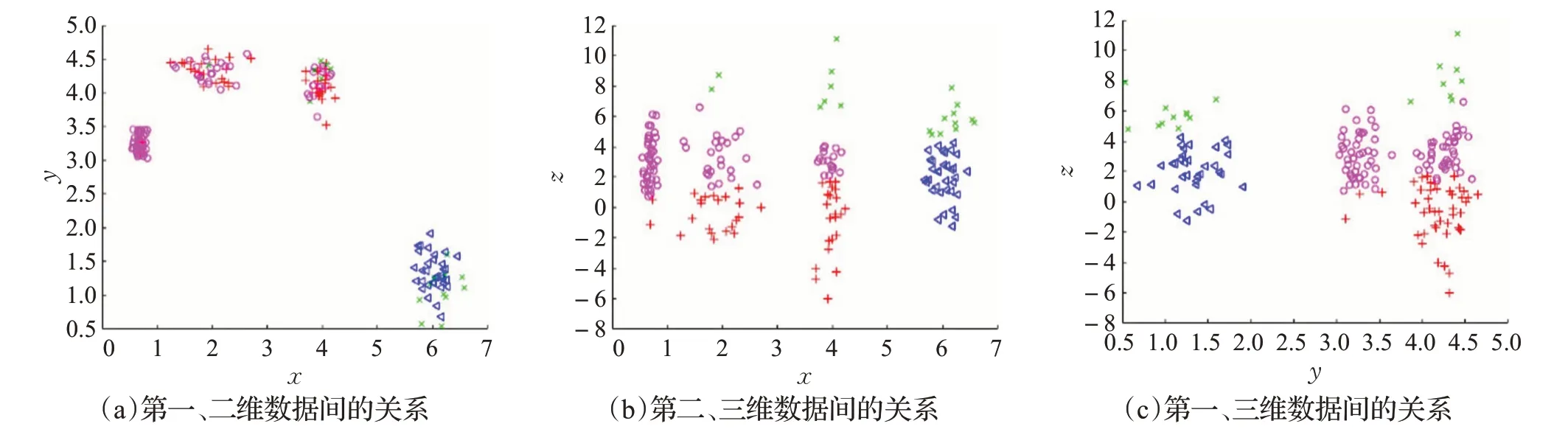
图8 k-means算法的聚类结果

图9 k-medoids算法的聚类结果

图10 MeanShift算法的聚类结果

图11 ENC算法的聚类结果

图12 WENC算法的聚类结果

对比图8～图12 可以观察出，该数据集中有一个特征属性较为离散，不利于聚类过程的进行。k -means、k -medoids、MeanShift、ENC 算法在聚类过程中均受到该特征属性的干扰，在图8～11（a）中，各簇的划分情况并不理想。而WENC算法利用权值降低该特征属性对聚类过程的影响，图12（a）中各簇的划分较为清晰，WENC算法的聚类结果更优。

由此可知，在进行聚类时，不同的特征属性对聚类过程的影响不同，将不利于聚类的特征属性的影响度降低后，可以提高聚类结果的质量。

3.2 算法描述

本文在弹性网络的基础上，引入机械函数和加权思想，构造新的能量函数，并利用极大熵原理确定数据点的概率分布，使算法更具有普适性。通过权值确定的策略，减小不利因素对聚类的影响，再计算自由能函数，当弹性节点每次迭代的位移量连续10次小于0.001时，网络停止运行并获得最后的聚类方案。该方法不仅提高了聚类质量，网络整体也比其他算法更加稳定。WENC算法的具体步骤如下：

（1）给定一个含有n 个数据点的数据集X={X1,X2,…,Xn} ，每个数据点均具有m 个特征属性Xi=(xi,1,xi,2,…,xi,m)。根据式（5）、式（6）分别计算每个特征属性的离散程度Gl和阈值V 。

（2）判断Gl是否大于阈值V ：若是，则根据式（7）计算该特征属性的权值ul；若否，则初始化该特征属性的权值ul=1。

（3）在数据空间内初始化一个含有k 个弹性节点的弹性带Y={Y1,Y2,…,Ym}，每个弹性节点均具有m 个特征属性Yj=(yj,1,yj,2,…,yj,m)。弹性带是以数据集的重心Xˉ为中心，R 为半径的封闭圆环，Xˉ、R 分别根据式（18）、式（19）计算获得，弹性节点均匀分布在弹性带上。

（4）根据式（13）计算数据点及相邻节点间的总能量，并由推导出的式（17）计算每次迭代弹性节点在每个特征维度上移动的距离Δyj,l。

（5）重复步骤（4），当弹性节点的移动量连续10 次小于0.001时，网络停止运行，此时弹性节点的位置即为各集群的中心点，即获得各簇的聚类中心点。

（6）计算数据点到各弹性节点的距离Di,j，并将数据点分配至距离该点最近的弹性节点，获得最终的聚类方案，完成聚类。Di,j如式（20）所示：

4 实验仿真

弹性网络具有非常好的几何特性，能够有效地解决固定目标函数求解极小值的问题，因此基于弹性网络的聚类算法虽然能够很好地对数据集进行聚类，但只适用于数值型数据集，非数值型数据集必须转换为数值型数据集后才能够进行聚类运算。

为验证WENC 算法是否能够有效提高聚类质量，本文采用了大量的随机数据集和真实数据集对其进行实验仿真。由于随机数据集没有标签，随机数据集的实验结果通过聚类标准SED 值来评价。真实数据集的实验结果通过SED 值和Accuracy 来评价。Accuracy 的计算方法如式（21）所示。

其中，ai为被正确分类的数据点的个数，N 为数据集中所有数据点的个数。

4.1 随机数据集

随机数据集生成的方法类似文献[31]，由Matlab程序生成。为使实验更具普适性，本文合成了含有不同特征属性、不同数量级的数据集。WENC算法中参数设置为β=1,Δτ=0.001,λ=0.5。每次实验的弹性带以实验数据的重心Xˉ为中心，半径R 通过式（19）确定。为显示WENC算法的优势，每组实验均与k-means、k-medoids、MeanShift以及未加权的弹性网络聚类算法ENC的结果进行对比。由于k-means、k-medoids 算法对初始中心点的位置非常敏感，分别对每组数据集进行20次测试，取结果的平均值进行比较。

为验证网络增加权值的有效性，本文首先选取了具有60、300、1 000个数据点的数据集，表3列出了各组数据集详细的聚类结果。

由表3 可以得到五种算法在不同维度下平均SED值的比较结果：对含有60、300、1 000个数据点的随机数据集，WENC算法求解的SED值比k-means算法分别减少7.51%、6.12%、1.82%，比k -medoids 算法分别减少8.93%、10.42%、7.57%，比MeanShift 算法分别减少8.67%、24.29%、19.53%，比ENC 算法分别减少2.65%、3.33%、7.99%。此外WENC网络运行多次结果不变，与k -means、k -medoids 算法相比，结果非常稳定，因此本文提出的WENC算法在解决聚类问题时不需要多次运行。综上，对不同的多维随机数据集，WENC 算法均可获得比k-means、k-medoids、MeanShift、ENC算法更好的聚类结果，验证了加权的有效性。此外加权提高了网络的求解速度，速度对比如图6所示。

为验证WENC 算法处理大规模数据集的能力，本文还对具有3 000、6 000、10 000个数据点，分为3簇、10簇的数据集进行实验。具体实验结果如表4所示。

由表4 可以得到五种算法在不同维度下的平均SED 值比较结果：对含有3 000、6 000、10 000 个数据点的随机数据集，WENC算法求解的SED值比k-means算法分别减少1.43%、0.87%、2.03%，比k-medoids 算法分别减少6.29%、5.15%、7.12%，比MeanShift 算法分别减少25.46%、20.98%、20.82%，比ENC 算法分别减少8.91%、3.55%、0.41%。此外WENC 网络运行多次结果不变，与k-means、k-medoids算法相比，结果非常稳定，分析对比如图1所示。综上，对不同的多维随机数据集，WENC 算法在处理大规模数据集方面均可获得比k -means、k-medoids、MeanShift、ENC算法更好的聚类结果。

表3 随机数据集聚类结果对比

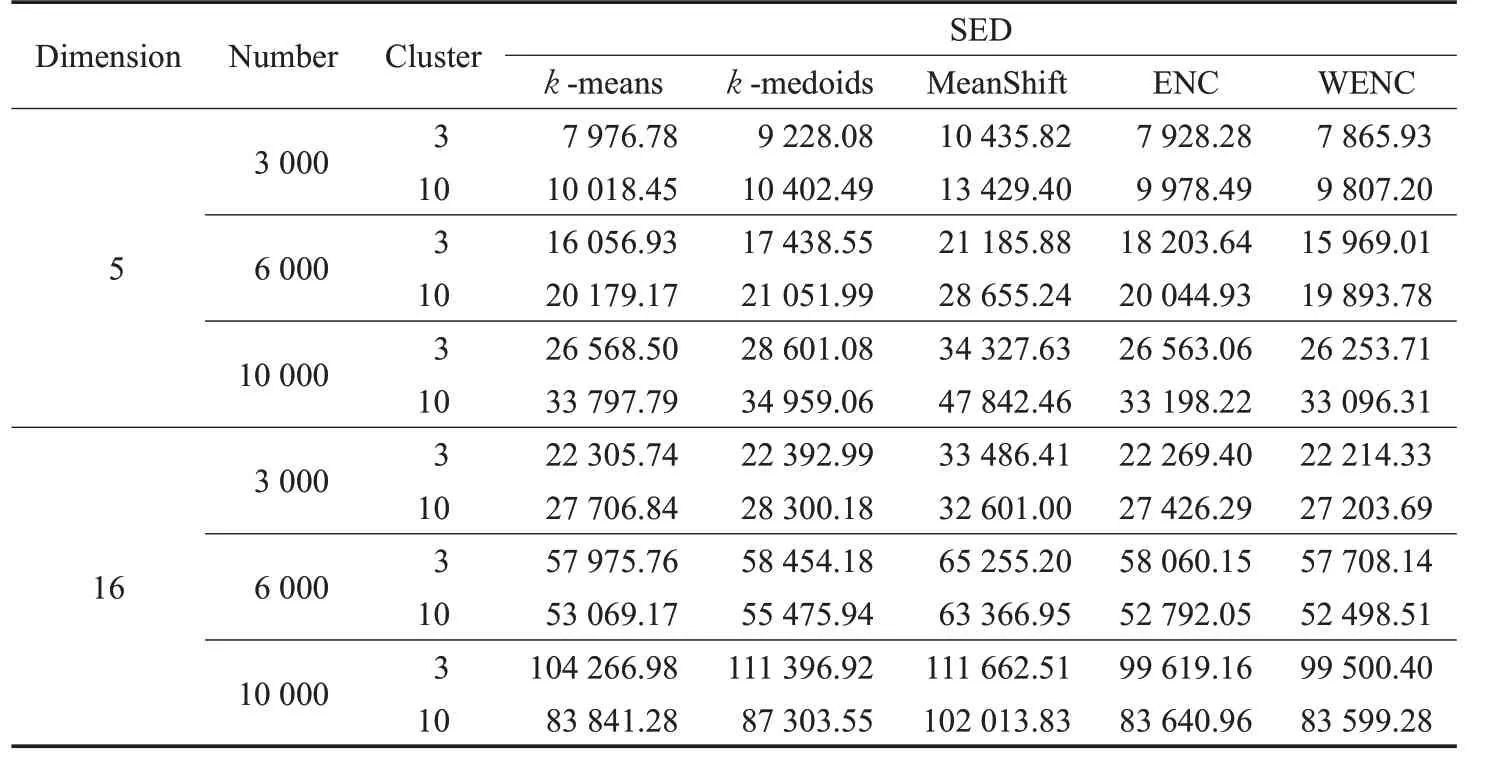
表4 大规模随机数据集聚类结果对比

表5 真实数据集聚类结果对比

4.2 真实数据集

真实数据集是从标准库UCI内获取的，与k-means、k-medoids、MeanShift算法进行了对比实验。本文选取Zoo、Seeds、Iris、Wine、Handwritten等数据集进行运算测试。其中Zoo 包含101 个数据样本，16 个特征属性，目标划分为7 簇；Seeds 包含210 个数据样本，7 个特征属性，目标划分为3 簇；Iris 包含150 个数据样本，4 个特征属性，目标划分为3簇；Wine包含178个数据样本，13个特征属性，目标划分为3 簇；Handwritten Digits（为方便记录，表中记为Hand）包含10 992 个数据样本，16 个特征属性，目标划分为10 簇。该实验使用与随机数据集实验相同的方法对聚类结果进行评估，并增加Accuracy聚类标准来多方面评估聚类结果。实验的详细结果如表5所示。

通过对比表5的数据结果可知，WENC算法在真实数据集中的聚类结果，与k-means 算法对比，SED 值分别降低20.68%、22.29%、7.54%、13.06%、9.65%，Accuracy分别提高19.70%、31.88%、18.33%、30.43%、8.82%；与k -medoids 算法结果对比，SED 值分别降低16.88%、21.25%、5.95%、13.06%、5.64%，Accuracy 分别提高16.18%、28.17%、9.23%、18.42%、17.46%；与MeanShift算法结果对比，SED值分别降低4.13%、2.21%、17.17%、0.69%、10.22%，Accuracy 分别提高9.72%、2.25%、10.94%、2.27%、25.42%。实验结果表明，WENC算法不仅提高了聚类质量，还优化了Accuracy，聚类结果得到有效改善。

由此分析，本文提出的WENC 算法无论对低维还是高维数据集的聚类能力均优于k-means、k-medoids、MeanShift 等传统算法。此外，WENC 算法在排除噪声因素干扰、稳定聚类的同时，保证了整个网络收敛。

5 结束语

本文针对聚类算法中存在的聚类结果易受噪声干扰、多维空间聚类质量不佳等问题，提出了一种具有加权特性的弹性网络聚类算法（WENC）。与传统聚类算法相比，本文选择适合求解固定目标函数极小问题的弹性网络模型。由于原始弹性网络不能直接用于解决聚类问题，本文在弹性网络基础上考虑到不同特征属性对聚类的重要程度不同，通过对数据集中某些影响聚类结果的特征属性进行加权，达到削弱这些特征属性在聚类过程中对网络影响的目的。基于以上原理，重新构建模型的能量函数，并结合极大熵原理确定数据集的概率分布。设置新的弹性网络目标函数，以达到聚类的目的。该算法中弹性网络初始弹性节点的数量与目标划分簇数相等，在网络利用模拟退火思想，不断给系统“降温”达到能量函数最小值时，弹性节点的位置即为聚类各簇中心点的位置。此外，由于更改了弹性节点初始化的个数，使得弹性网络针对聚类问题可以求解含有近一万个样本点的多维数据集，显著提高了求解问题的规模。最后，在不同维度、不同数量级的随机数据集以及UCI 真实数据集上进行了实验，并分别利用聚类内部评价标准SED 值和聚类外部评价标准Accuracy 对聚类结果进行评估，结果表明，WENC 算法能够对高维数据集稳定地提供更好的聚类方案。