高校供热系统调控策略优化研究

王睿鑫， 周志刚， 荆 强， 谌薛蛟

(哈尔滨工业大学 建筑学院，黑龙江哈尔滨150006)

1 概述

目前，我国北方城镇集中供热面积达到91.4×108m2，建筑供暖能耗占建筑总能耗的24.1%[1]。高校建筑由于建筑类型杂，体量大，在建筑供暖能耗中占有相当大的比重。据统计，高等院校的人均能源消耗是普通居民的4倍，北方高校供暖能耗已达学校整体能耗的50%以上，位居高校能耗首位[2]。因此，供热系统的节能优化是高等院校节能工作的重点。高校供热系统的运行控制是节能的关键，在寻找合理的调控策略过程中，许多学者以负荷优化为目标研究了供热系统的部分负荷特性、影响因素[3-4]以及负荷预测方法[5-6]。部分学者则以多种能源供给为前提，研究了供热参数调控优化算法[7-8]。

本文针对北方高校，以稳态传热模型为基础，开发包含热源、二级管网、建筑在内的供热系统仿真模型。结合校园建筑分时段使用的特点，提出供热系统启停、建筑使用期间室温调控优化方法。采用仿真模型，对优化后的调控策略效果进行模拟分析。

2 高校供热系统仿真模型

2.1 数学模型

供热系统数学模型架构见图1。由图1可知，供热系统数学模型涵盖了热力站模型、二级管网模型、用户模型。

图1 供热系统数学模型架构

① 热力站模型

换热器一级侧热平衡关系式为：

式中m1——换热器一级侧水的质量，kg

cp,1——换热器一级侧水的比定压热容，J/(kg·K)

θ1,out——换热器一级侧出水温度，℃

t——时间，s

qm,1——换热器一级水的质量流量，kg/s

θ1,in——换热器一级侧进水温度，℃

K——换热器的传热系数，W/(m2·K)

A——换热器的换热面积，m2

Δtm——换热对数平均温差，℃

换热器二级侧热平衡关系为：

式中m2——换热器二级侧水的质量，kg

cp,2——换热器二级侧水的比定压热容，J/(kg·K)

θ2,out——换热器二级侧出水温度，℃

qm,2——换热器二级水的质量流量，kg/s

θ2,in——换热器二级侧进水温度，℃

② 二级管网模型

由热平衡关系，得到二级管网模型为[9]：

式中C——管网的热容，J/K

θout——管网的出水温度，℃

cp——管网中水的比定压热容，J/(kg·K)

qm——管网中水的质量流量，kg/s

θin——管网的进水温度，℃

Kp——管中水与土壤间的传热系数，W/(m2·K)

Ap——管子的散热面积，m2

θsoil——土壤温度，℃

③ 热用户模型

由热平衡关系，得到散热器模型为：

式中Cs——散热器热容，J/K

θs,out——散热器的出水温度，℃

cp,s——散热器内水的比定压热容，J/(kg·K)

qm,s——散热器中水的质量流量，kg/s

θs,in——散热器的进水温度，℃

Ks——散热器的传热系数，W/(m2·K)

As——散热器的传热面积，m2

θr——室内温度，℃

围护结构的传热可以近似为一维导热，围护结构模型为：

hw,outAw,out(θw,out-θo)

式中Cw——墙体的热容，J/K

θw,in——墙体内表面温度，℃

hw,in——墙体内壁表面传热系数，W/(m2·K)

Aw,in——墙体内壁传热面积，m2

hw,out——墙体外壁表面传热系数，W/(m2·K)

Aw,out——墙体外壁传热面积，m2

θw,out——墙体外表面温度，℃

θo——室外温度，℃

忽略太阳辐射得热量、室内人员及设备散热，室温模型为[10]：

hw,inAw,in(θr-θw,in)-KcAc(θr-θo)-

0.278ρacp,aVr(θr-θo)

式中Cr——房间的热容，J/K

Kc——外窗传热系数，W/(m2·K)

Ac——外窗面积，m2

ρa——空气密度，kg/m3

cp,a——空气的比定压热容，kJ/(kg·K)

Vr——房间的容积，m3

2.2 仿真模型

根据数学模型，采用TRNSYS构建校园供热系统仿真模型。模拟对象为哈尔滨某高校供热系统，室内采用散热器供暖系统，总供热面积为7.9×104m2，总设计热负荷为7 745 kW。供暖室内设计温度为18 ℃，供暖室外计算温度为-24.2 ℃，室外的平均风速为3.2 m/s。建筑热力入口安装分时供热控制器、电动调节阀、热量表，供回水管安装温度、压力传感器。热力站采用质-量并调方式，二级循环泵为变频泵。供热系统平面布置见图2。

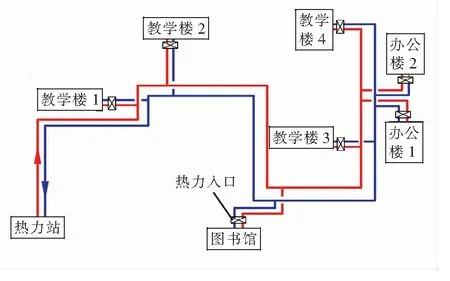
图2 供热系统平面布置

TRNSYS仿真系统见图3。室外气象参数来自国家气象局网站，由室外气象模块调用对应模拟时间段内的气象参数。

图3 TRNSYS仿真系统(软件截图)

TRNSYS仿真系统主要组件包括建筑物模块、室外气象模块、时间控制模块、计算模块。供热系统包含7幢建筑(见图2)，建筑几何模型(见图4)按实际结构尺寸构建，利用SketchUp软件建立。建筑几何模型以特定文件形式储存，可被TRNSYS软件中的建筑物模块调用。围护结构参数在建筑物模块中进行设置，围护结构参数见表1。外窗为双层玻璃塑钢窗，传热系数为2.0 W/(m2·K)。

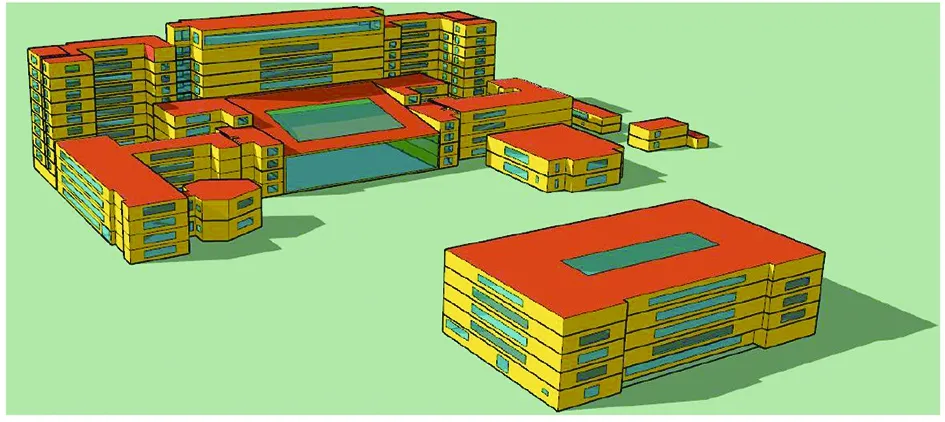
图4 建筑几何模型

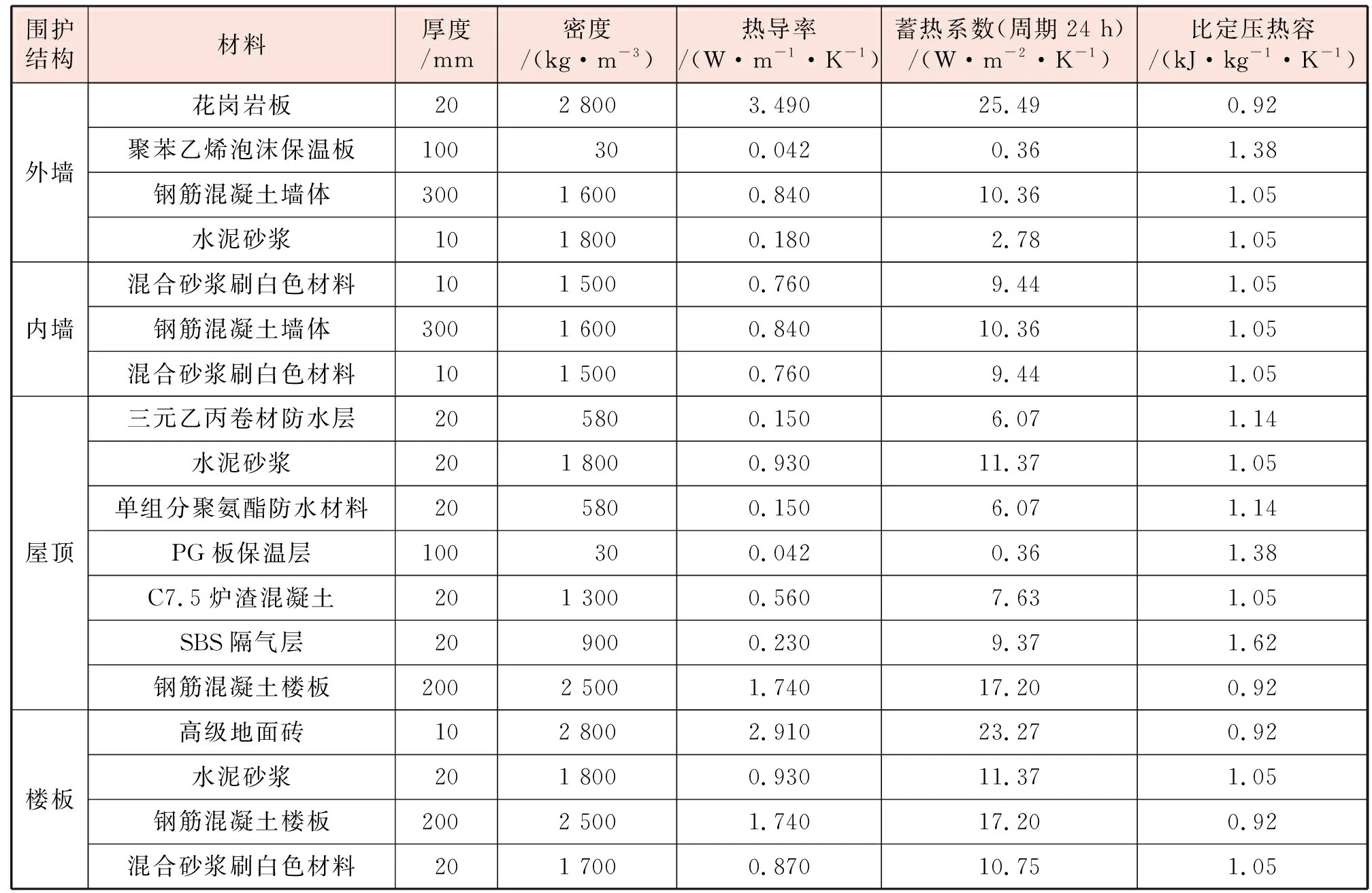
表1 建筑物围护结构参数

2.3 模型验证

利用TRNSYS仿真模型模拟各建筑2020年1月20日—23日的室内温度，以相同时段的实测数据进行验证。各建筑室内温度仿真值与实测值的最大误差、标准差见表2，各建筑模拟日供暖能耗的仿真值与实测值的相对误差见表3。

表2 各建筑室内温度仿真值与实测值的最大误差、 标准差

由表2可知，对于室内温度，仿真值与实测值的最大误差不超过1.3 ℃，标准差不超过0.6 ℃。由表3可知，对于供暖能耗，仿真值与实测值的最大相对误差为5.19%，平均相对误差不超过3%。这表明仿真结果可信。

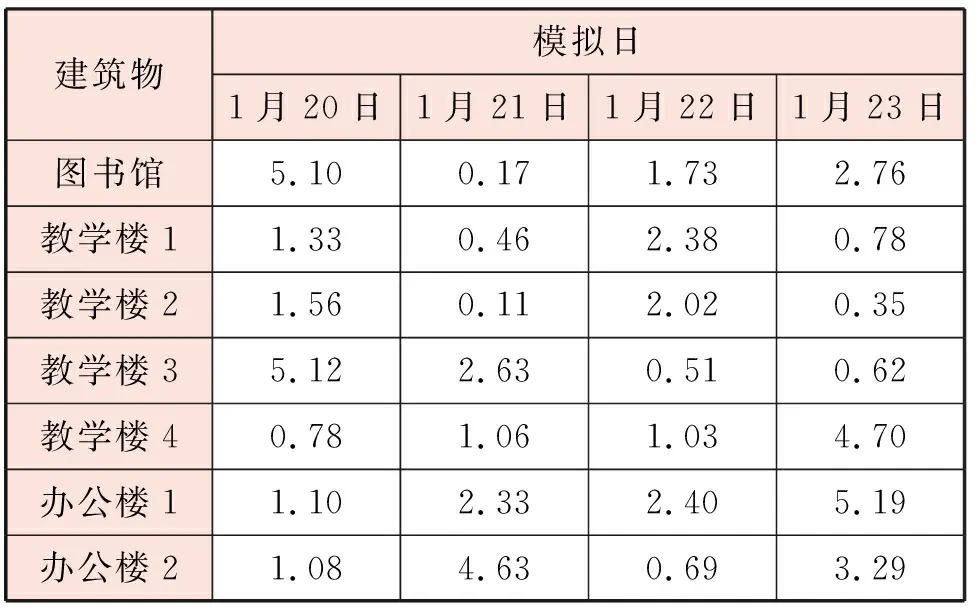
表3 各建筑模拟日供暖能耗的仿真值与实测值的相对误差 %

3 调控策略优化方法

3.1 启停优化

高校建筑的运行时间为8:00—22:00，由此制定的室内目标温度分时控制原则见图5。由图5可知，分时控制原则是在夜间仅满足室内供暖系统防冻需要(室内最低温度5 ℃)，并保证建筑在开始使用时室内温度满足要求。实际上，得益于建筑热惰性的作用，停热期间室内温度为缓慢下降过程，这也为供热开始后室内温度迅速回到设计温度提供了条件。

图5 室内目标温度分时控制原则

常见的启停策略往往根据经验，在建筑开始使用前的3～5 h供热，在建筑结束使用时停热。但这种启停策略缺少理论依据，导致在建筑使用时间外，也保持了较高的室内温度。

笔者利用仿真模型，模拟了2019—2020年供暖期，不同室外平均温度(指供热开始至建筑开始使用期间的室外平均温度)下，不同供热开始时间的室内温升(指供热开始时间至8:00的室内温升)，以及不同室外平均温度(指停热至建筑停止使用期间的室外平均温度)下，不同停热时间的室内温降(指停热时间至22:00的室内温降)，分别见图6、7。由图6可知，相同室外平均温度下，供热开始时间越早，室内温升越大。由图7可知，相同室外平均温度下，停热时间越晚，室内温降越小。因此，对于具体项目，可根据仿真结果选取供热开始时间、停热时间，对启停策略进行优化。

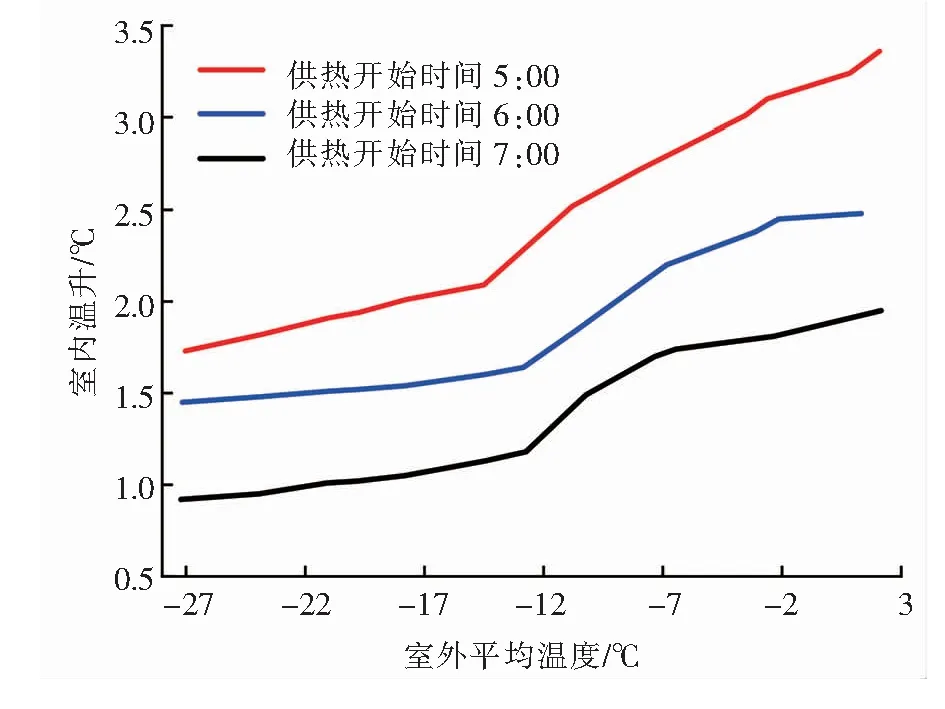
图6 不同室外平均温度下不同供热开始时间的 室内温升

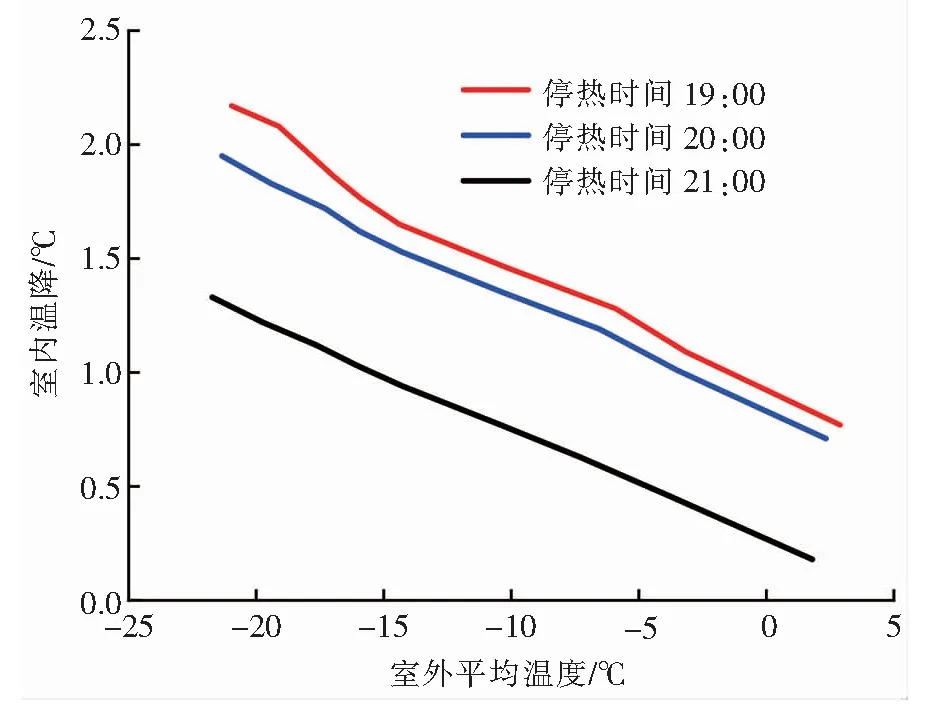
图7 不同室外平均温度下不同停热时间的室内温降

根据仿真结果，对室内温升、温降与室外平均温度的关系式分别进行拟合。

① 室内温升

供热开始时间为5:00时，室内温升与室外平均温度的关系式为：

Δθr,r=0.062θo,av+3.2

式中 Δθr,r——室内温升，℃

θo,av——室外平均温度，℃

供热开始时间为6:00时：

Δθr,r=0.043θo,av+2.4

供热开始时间为7:00时：

Δθr,r=0.041θo,av+1.88

② 室内温降

停热时间为19:00时，室内温降与室外平均温度的关系式：

Δθr,d=-0.057θo,av+0.91

式中 Δθr,d——室内温降，℃

停热时间为20:00时：

Δθr,d=-0.051θo,av+0.825

停热时间为21:00时:

Δθr,d=-0.048θo,av+0.27

3.2 建筑使用期间的室温调控策略优化

建筑使用期间的室温调控策略优化主要是根据室外温度、供暖室内计算温度预测热负荷，调节热力入口电动调节阀相对开度(本文将建筑使用期间的室温调控优化方法称为热力入口电动阀室温调控)。实现按需供热，提高供热质量，保持良好的经济性。热力入口电动阀室温调控流程见图8。每15 min读取1次当前室内温度，是否有阀门开度调节操作的判定时间t为15 min。建筑使用期间的室内温度控制范围取18～20 ℃。

图8 热力入口电动阀室温调控流程

利用机器学习中的监督学习方式计算热力入口电动调节阀相对开度，并建立相应的回归模型。考虑到供热数据规模比较小，执行机构(热力入口电动调节阀)相对简单，复杂、多权重、多参数的算法模型并不适用。线性回归算法作为机器学习中较为基础的一种，具有简单、建模迅速、容易实现的特点，对小数据量、简单的关系很有效。而且训练和预测速度比较快，结果具有很好的可解释性，因此本文采用线性回归算法。优化训练数据为340组，验证集数据为120组。

热力入口电动调节阀目标相对开度ka的回归模型为：

ka=β0+β1k+a(θr,ac-θr,ai)

式中ka——热力入口电动调节阀目标相对开度

β0、β1——参数

k——当前相对开度

a——室内温度升高1 ℃阀门相对开度减小的步长

θr,ac——实际室温，℃

θr,ai——目标室温，℃

采用最小二乘法的训练结果为：

ka=0.066+0.919k-0.14(θr,ac-θr,ai)

采用平均绝对误差MAE、均方根误差RMSE、相关指数R2作为验证集的评价指标，计算结果分别为0.016、0.02、0.979。由计算结果可知，热力入口电动调节阀目标相对开度回归模型效果精确度比较高。

4 结果与讨论

以教学楼1～4作为分析对象，选择2019—2020年供暖期的严寒期、末寒期各1个典型日作为模拟时段。严寒期选择1月8日8:00至1月9日8:00(以下简称严寒日)，末寒期选择3月10日8:00至3月11日8:00(以下简称末寒日)。设定1月8日8:00、3月10日8:00初始室温为18 ℃，热力入口电动调节阀初始相对开度为0.71。

4.1 调控策略1

调控策略1：3:00供热，22:00停热，在建筑使用期间，二级管网流量固定，热力入口电动调节阀保持初始相对开度不变。

调控策略1下严寒日、末寒日室内温度、室外温度随时间的变化分别见图9、10。由图9、10可知，调控策略1下，严寒日、末寒日教学楼使用期间的室内温度均满足甚至高于要求。22:00停热后室内温度经过快速下降后变得缓慢，这主要得益于建筑热惰性。由于供热开始时间过早，建筑非使用期间室内温度偏高，1月9日8:00、3月11日8:00室内温度分别达到了19.5、21.8 ℃，存在着较为严重的过量供热问题。

图9 调控策略1下严寒日室内温度、室外温度 随时间的变化

图10 调控策略1下末寒日室内温度、室外温度 随时间的变化

4.2 调控策略2

调控策略2(启停策略优化后)：严寒日停热时间为21:00，供热时间为5:00。末寒日停热时间为19:00，供热时间为7:00。在建筑使用期间，二级管网流量固定，热力入口电动调节阀相对开度保持初始相对开度不变。

调控策略1、2下严寒日、末寒日室内温度随时间的变化分别见图11、12。由图11、12可知，与调控策略1相比，由于调控策略2进行了启停策略优化，进一 步提前停热、延后供热，仍能满足建筑使用期间的室内温度要求，建筑非使用时段的室内温度也明显合理。建筑热惰性确保了停热后室内温度的有限下降，严寒日供热开始时，室内温度为16.6 ℃；末寒日供热开始时，室内温度为17.9 ℃。

图11 调控策略1、2下严寒日室内温度随时间的变化

图12 调控策略1、2下末寒日室内温度随时间的变化

4.3 调控策略3

调控策略3(启停优化策略+热力入口电动阀室温调控)：严寒日停热时间为21:00，供热时间为5:00。末寒日停热时间为19:00，供热时间为7:00。在建筑使用期间，调节热力入口电动调节阀相对开度，使室内温度保持在18～20 ℃。

调控策略2、3下严寒日、末寒日室内温度随时间的变化分别见图13、14。由图13、14可知，与调控策略2相比，运行策略3可将建筑使用期间的室内温度控制在要求范围内，进一步降低供热能耗。

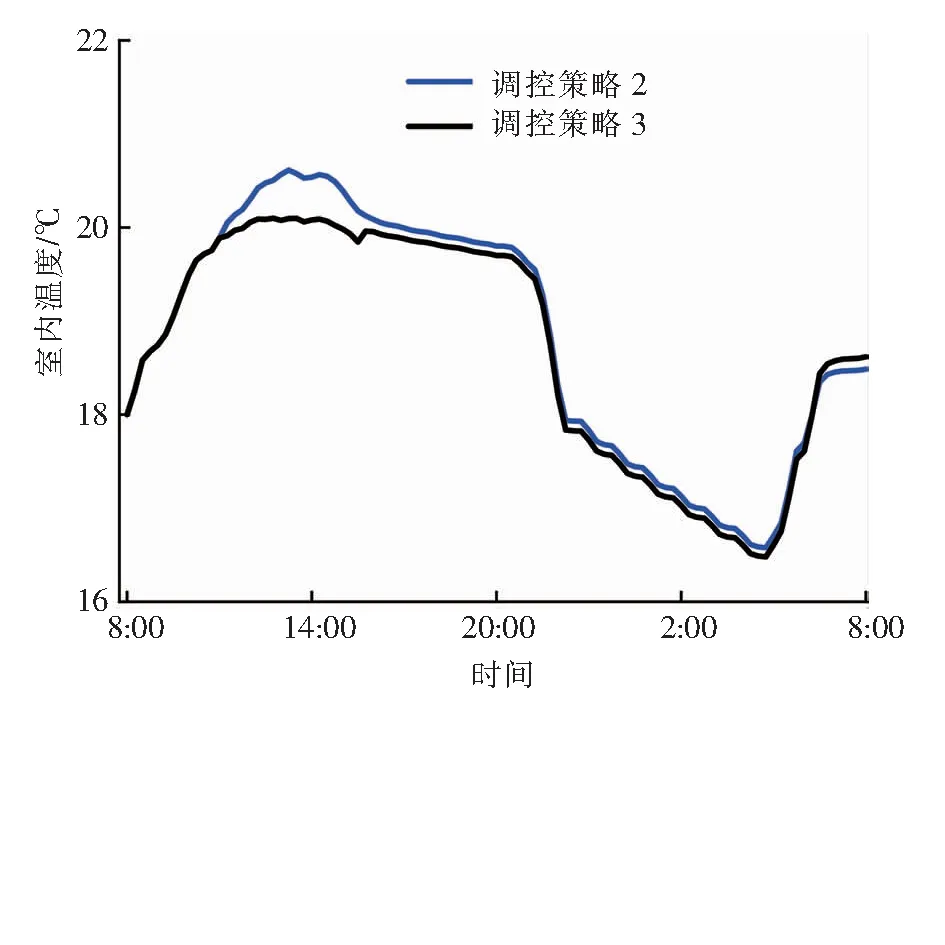
图13 调控策略2、3下严寒日室内温度随时间的变化

图14 调控策略2、3下末寒日室内温度随时间的变化

4.4 优化效果

采取启停优化策略+热力入口电动阀室温调控，不仅使建筑使用期间的室内温度控制在要求范围内，还利用建筑热惰性确保停热后室内温度的有限下降，有利于降低供热能耗。

5 结论

① 以稳态传热模型为基础，开发的供热系统(包含热力站、二级管网、建筑)仿真模型的仿真结果可信。

② 调控策略1下，严寒日、末寒日教学楼使用期间的室内温度均满足甚至高于要求。22:00停热后室内温度经过快速下降后变得缓慢，这主要得益于建筑热惰性。由于供热开始时间过早，建筑非使用期间室内温度偏高，1月9日8:00、3月11日8:00室内温度分别达到了19.5、21.8 ℃，存在着较为严重的过量供热问题。

③ 与调控策略1相比，调控策略2进行了启停策略优化，进一步提前停热、延后供热，仍能满足建筑使用期间的室内温度要求，建筑非使用时段的室内温度也明显合理。建筑热惰性确保了停热后室内温度的有限下降，严寒日供热开始时，室内温度为16.6 ℃；末寒日供热开始时，室内温度为17.9 ℃。

④ 与调控策略2相比，调控策略3可将建筑使用期间的室内温度控制在要求范围内，进一步降低供热能耗。

⑤ 采取启停优化策略+热力入口电动阀室温调控，不仅使建筑使用期间的室内温度控制在要求范围内，还利用建筑热惰性确保停热后室内温度的有限下降，有利于降低供热能耗。