亚微米颗粒物湍流团聚数值模拟研究
冯 鹏,盛 虎,周 虎,王承亮,刘鹤欣,李正鸿,谭厚章,杨富鑫
(1.西安交通大学 热流科学与工程教育部重点实验室,陕西 西安 710049;2.华电章丘发电有限公司,山东 济南 250216)
0 引 言
细颗粒物排放是造成大气污染的重要原因之一,其中亚微米颗粒粒径小于1 μm,比表面积大,易富集有毒污染物[1]。工业用煤燃烧过程中产生的亚微米颗粒物已成为大气中亚微米颗粒物的主要来源[2]。控制亚微米颗粒物排放对我国可持续发展能源战略有重大意义[3]。静电除尘器、布袋除尘器对粒径大于2 μm的颗粒物有很高的脱除效率,但对亚微米颗粒物的脱除效率相对较低,存在穿透窗口[4-5]。在静电除尘器前的尾部烟道内,安装相关的团聚装置,促进亚微米颗粒物团聚形成较大的颗粒物,可提高除尘效率,减少亚微米颗粒物的排放[6]。湍流团聚通过在传统工业除尘设备前端增加团聚装置以促进亚微米颗粒物的长大,进而提高传统除尘器对亚微米颗粒物的脱除效率。
大量学者对湍流团聚技术进行研究。数值模拟方面,早期研究主要集中在不同惯性颗粒物碰撞核理论分析与模型建立上,Saffman和Turner[7]基于球碰撞理论提出了零惯性颗粒在均匀各向同性的湍流中的碰撞模型;Abrahamson[8]建立了大惯性粒子的湍流碰撞核模型。Otto等[9]考虑了布朗运动对颗粒物在流场中运动的各种影响,提出了涵盖整个粒径范围的布朗碰撞核方程。Zaichik等[10]提出了颗粒物局部富集效应的湍流团聚核函数;Chi和Sommerfeld[11]考虑均匀各向同性湍流并发展了随机拉格朗日团聚机理,给出计算颗粒物是否团聚的临界速度。郑建祥等[12]在模拟颗粒物团聚过程中加入排斥势能作用,引入捕集效率修正颗粒物聚并模型,修正后的模型与试验结果吻合度大于97%;刘忠等[13]模拟了湍流聚并器中不同粒径颗粒物的运动轨迹,增大流速以及颗粒物荷电可以增加粒子碰撞概率。章鹏飞等[14]对Z型扰流元件进行了数值模拟研究,探究了烟气流速对细颗粒物湍流聚并的影响,发现聚并的效果随着流速的增大而提高。试验方面,孙德帅等[15]搭建可吸入颗粒物射流团聚试验系统,研究了不同射流条件对细颗粒物碰撞聚并的影响。陈冬林等[16]将超细颗粒物物湍流团聚装置应用于300 MW燃煤机组。
综上所述,许多研究都集中在理论分析和建模上,但鲜见扰流件的形状对颗粒物团聚的影响。本文同时考虑湍流和布朗运动引起的颗粒物团聚,建立数值模型来分析不同烟气流速对颗粒物团聚特性的影响以及亚微米颗粒物在不同形状扰流件中的团聚情况。
1 试验与数值模拟
1.1 试验系统
亚微米颗粒物团聚的试验系统如图1所示。通道中的气流由鼓风机提供。由气溶胶发生器产生亚微米颗粒物,经干燥后进入流道,在团聚试验段内布置一系列三棱柱扰流件,使亚微米颗粒物在试验段内发生湍流团聚,团聚段前后有足够距离保证颗粒物扩散均匀。在试验段前后设置2个测点,对15.7~850.5 nm亚微米颗粒物数量浓度进行实时监测。
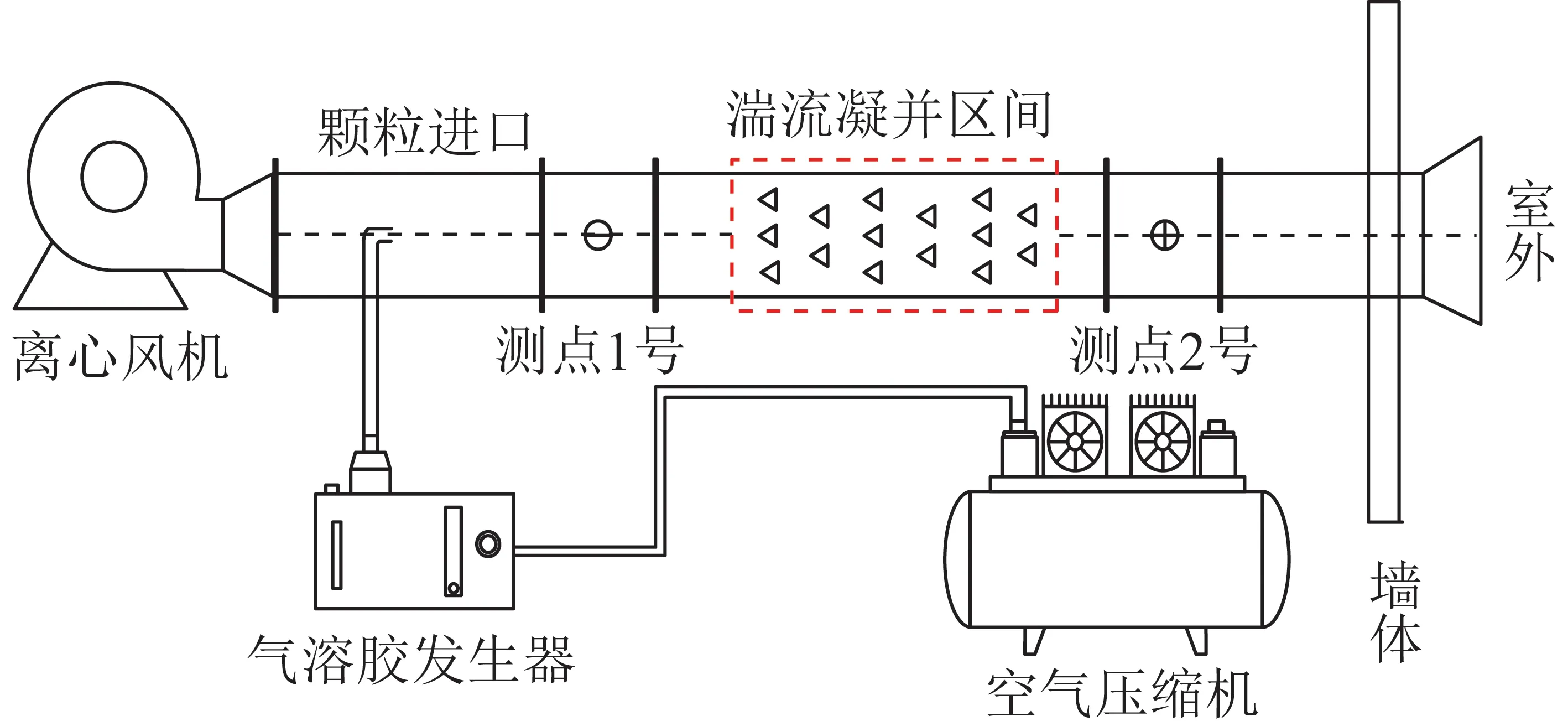
图1 亚微米颗粒物湍流团聚试验台Fig.1 Testbed for the submicron particle turbulent agglomeration
1.2 物理模型与网格划分
湍流团聚段示意如图2所示,通道宽高为150 mm×100 mm,团聚区间长度为900 mm,三棱柱形状扰流底部三角形边长为5 mm,采用错排结构布置扰流件。模拟计算网格由ANSYS CFD ICEM 17.0生成,如图3所示。计算区域的大小与试验团聚段的大小相同。对壁面处的边界层区域和扰流件尾迹区域进行了局部网格加密,取X轴方向一个横截面上的3根关于X轴对称的线的线速度来验证网格的独立性。最后,确定网格数量为1 423 912个。另外,时间步长设为0.002 s。
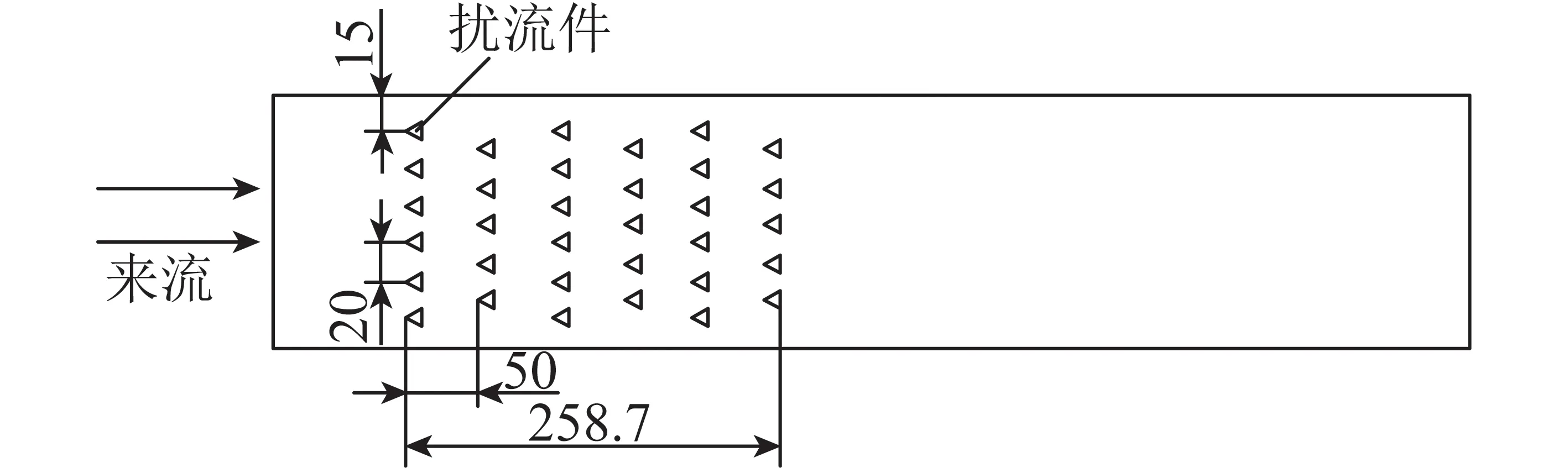
图2 试验团聚段布置示意Fig.2 Schematic diagram of turbulence coalescence device in experiment

图3 团聚段计算网格Fig.3 Computational grids of the agglomeration segment
1.3 数学模型
采用Eulerian-Lagrangian模型,假设气体为连续介质,用欧拉坐标系描述气相流动,将固相看作离散颗粒物,在拉格朗日坐标系中计算颗粒物运动以及颗粒物与流场、颗粒物与颗粒物间相互作用。
气相控制方程基于Eulerian框架求解三维不可压缩流体N-S,即
·u=0,
(1)
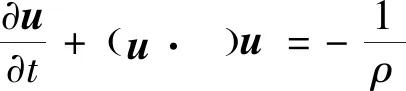
(2)
式中,u为笛卡尔坐标系下的流体速度矢量,m/s;t为时间,s;p为气体静压,Pa;ρ为流体密度kg/m3;ν为运动黏度,m2/s;Fb为体积力,N。
颗粒轨道方程根据Langrangian方程积分得出
(3)
式中,τ为颗粒物的速度矢量,m/s;g为重力加速度,m/s2;ρp为颗粒物密度;FD·(u-τ)为颗粒物受到的拖曳力,N;F为颗粒物受到的附加作用力,N。
1.4 颗粒碰撞模型
本文考虑颗粒物的碰撞核函数包括布朗运动与其受到湍流影响的共同作用。由于颗粒物碰撞受到湍流与布朗运动的影响尺度不同,故认为二者相互独立[17],因此综合两种运动产生的碰撞核函数为
(4)
式中,K为碰撞核函数,下标t和B分别为湍流碰撞核与布朗碰撞核。
布朗运动是引起颗粒物无规则运动的一个重要原因,许继云等[18]利用可视化系统观测颗粒物在流场内的运动轨迹,并结合数值模拟分析出试验观测到颗粒随机晃动可由布朗运动解释,因此布朗运动引起的颗粒物碰撞不可忽视。布朗运动所引起的颗粒物碰撞,无量纲数Kn起重要作用,其物理意义为流体分子平均自由程与颗粒物半径之比,即
(5)
其中,dp为颗粒物粒径,m;λ为流体分子自由程,m,可以由式(6)[19]计算
(6)
式中,T0=296.15 K;P0=1.013×105Pa;λ0为常温常压下空气分子的平均自由程,一般取67.3 nm;TS=110.4 K;T为环境气体绝对温度,K;p为环境气体压强,Pa。
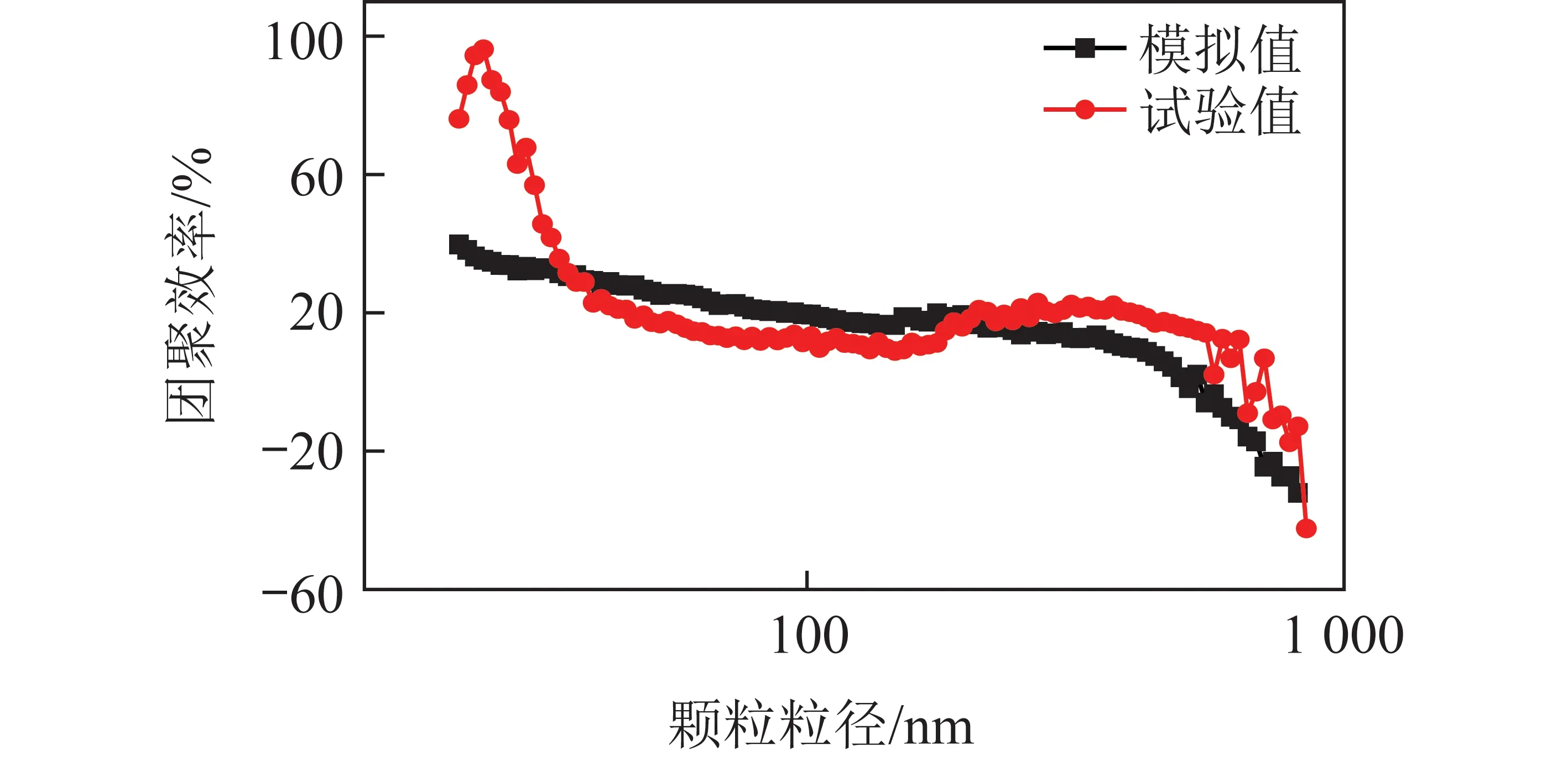
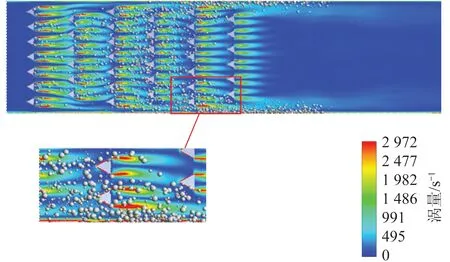
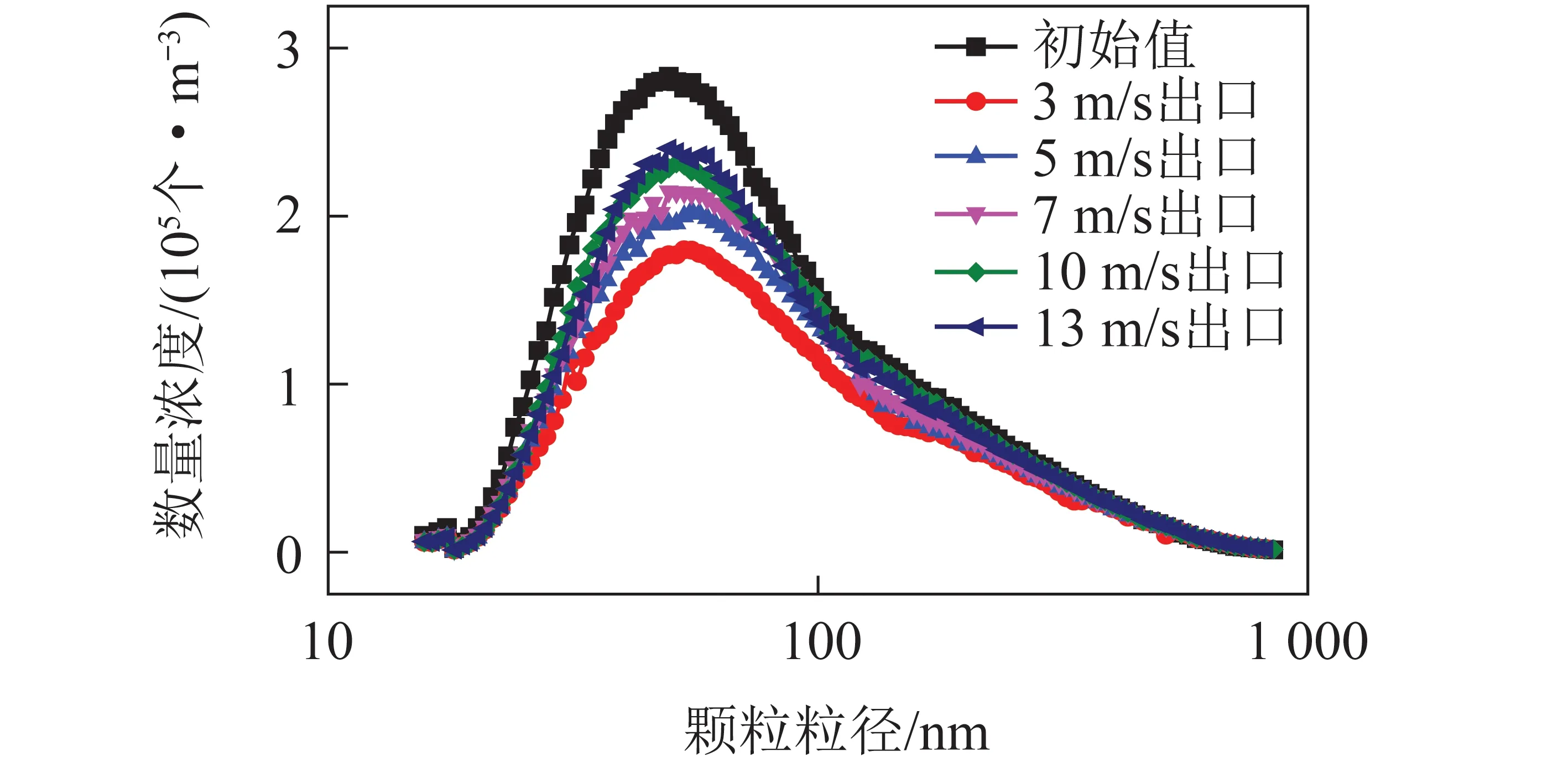
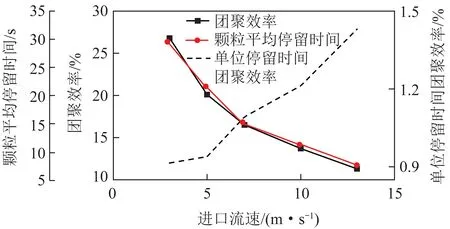
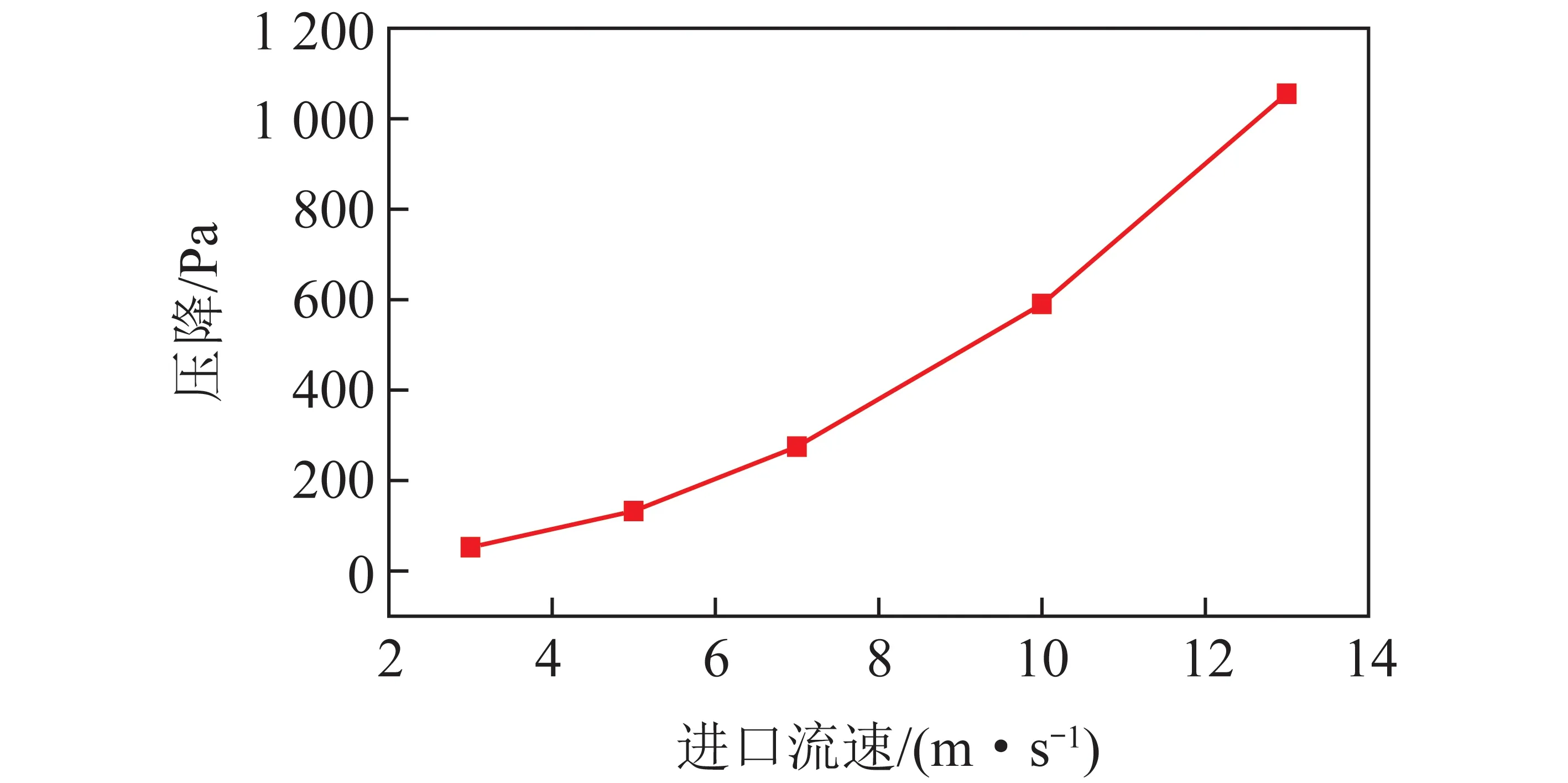
根据颗粒物的Kn不同可将颗粒物分为自由分子区、过渡区、近连续区和连续区。经计算本文采用颗粒物大部分处于过渡区(1 KB-t=KB-co/sff(Kn)。 (7) 采用Otto等[9]提出的修正因子模型 (8) (9) 连续区和近连续区的布朗碰撞核KB-co/sf为 (10) 自由分子区的布朗碰撞核KB-fm可以表示为 (11) (12) 式中,μ为流体的动力黏度,N·s/m2;V1、V2分别为2个相互碰撞颗粒物的体积,m3;kfm为自由分子区的碰撞系数;kB为玻尔兹曼常数。 在颗粒物-流体两相流中通常根据Stokes数(以下简称St)将颗粒物分为3类:零惯性颗粒物、有限惯性颗粒物、极大惯性颗粒物。St数表示为 (13) 式中,ε为湍流耗散率,m2/s3;ρf为流体密度,kg/m3。 由于本文所关注的亚微米颗粒物St数极小,故选用Saffman & Turner提出的零惯性湍流碰撞核。 (14) 式中,r1、r2为2个相互碰撞的颗粒物半径,m。 以上假设和碰撞核函数均使用Fluent中的用户自定义函数形式加入计算模型。 模拟时首先利用standardk-ε湍流模型在稳态条件下进行连续相计算,得到一个湍流初场,压力、湍动能、湍流耗散率采用二阶迎风格式。随后采用 DPM模型进行颗粒相计算,引入颗粒群(parcel)概念,从入口表面处释放parcel。颗粒相物理模型不考虑颗粒物的破碎和相变,忽略颗粒物之间的静电力,颗粒物发生碰撞并符合团聚条件时团聚生成一个颗粒物体积为碰撞之前颗粒物体积之和的大颗粒物。颗粒物的湍能耗散采用随机游走模型。入口流速为5 m/s,与试验时风速一致;颗粒物密度取2 100 kg/m3。壁面及扰流件均设置为无滑移反弹类壁面条件,出口采用充分发展管流条件,时间步长采用0.002 s,计算过程中,在出口截面采样,统计通过出口截面的颗粒物的粒径分布。 为与试验对比,计算时设置的初始颗粒物粒径分布根据初始颗粒物粒径分布得到。试验以及3种k-ε湍流模型下模拟计算得到的亚微米颗粒物的团聚效率如图4所示。团聚效率为正值说明亚微米颗粒物经过团聚段后小粒径颗粒物减少、大粒径颗粒物增多,小粒径颗粒物的团聚效率明显大于大颗粒物,从粒径593.5 nm开始团聚效率变为负值,主要原因是小粒径颗粒物惯性较小,易随涡流运动,造成局部富集增加碰撞团聚几率,另一方面是小颗粒物团聚成大颗粒物后没有继续团聚为更大粒径的颗粒物,使这部分颗粒物增多,团聚效率降低。 图4 试验与模拟计算的团聚效率对比Fig.4 Comparison of agglomeration efficiency between numerical and experimental values 团聚前后3种湍流模型计算出的亚微米颗粒物团聚效率试验值为16.4%,模拟值为20.1%。结合图4可知,模拟结果与试验结果趋势基本一致,但存在一定偏差,尤其是粒径15.7~23.3 nm,主要原因是本文计算模型未考虑壁面对颗粒物的吸附效应[22]。亚微米颗粒物在涡量场中的分布如图5所示。可以看出,由于团聚段内存在大量产涡扰流件,亚微米颗粒物被涡流卷吸运送至壁面处,增加了颗粒物沉积在壁面的几率,从而影响湍流团聚过程。其他可能造成偏差的原因还包括模型的精确度、试验本身的测量误差等。总体而言,模拟计算结果可以反映实际湍流团聚情况。 图5 某一时刻涡量场中的亚微米颗粒物分布Fig.5 Particle distribution in vorticity field at a certain time 为了研究不同烟气流速下亚微米颗粒的团聚情况,计算了3、5、7、10、13 m/s五种入口流速的工况。连续相采用standardk-ε湍流模型,初始粒径分布以及数值计算设置与2.1节相同。入口的初始颗粒物粒径分布以及各个入口流速下出口截面的颗粒物粒径分布如图6所示。可知5种流速均可使亚微米颗粒物发生湍流团聚,出口粒径分布的峰值相较于初始值均向大粒径方向偏移,证明了湍流团聚对粒径分布的影响。随流速升高,亚微米颗粒物的团聚效果逐渐减弱,在40.0~68.5 nm最为明显。 图6 不同流速下进出口亚微米颗粒物粒径分布Fig.6 Particle size distribution at inlet and outlet under different velocities 烟气进口流速对亚微米颗粒物的影响主要包括2方面:一是影响着流场中湍流耗散率大小,本文采取的湍流碰撞核函数与流场有关的物理量只有湍流耗散率,因此湍流耗散率大小对亚微米颗粒物的碰撞团聚起一定作用;另一方面,随着进口流速的增加,亚微米颗粒物在团聚试验段内的停留时间也随之减少,不利于颗粒物团聚。 不同流速下亚微米颗粒物的团聚效率以及颗粒物平均停留时间如图7所示。随流速升高,二者均下降,缩短停留时间会降低颗粒物团聚效率,但单位停留时间下的团聚效率随流速的升高而升高,主要是由于流速升高,流场内各处的湍流耗散率升高。因此选择进口流速时,既要保证流场中湍流耗散率的大小,又要兼顾颗粒在流场中的停留时间。 图7 不同流速下亚微米颗粒物的团聚效率以及平均停留时间Fig.7 Agglomeration efficiency and average residence time of submicron particles under different velocities 不同流速下亚微米颗粒物数量浓度及团聚效率变化见表2,可知PM0.1的团聚效率随流速变化趋势与PM1相同,两者在3 m/s工况下团聚效率最高,分别为26.8%和36.2%。各流速下,PM1的团聚效率均小于PM0.1,这是因为小粒径颗粒物惯性小在涡流里的跟随性更好,直到其团聚为大颗粒物才会脱离涡流流出团聚段,值得注意的是PM1和PM0.1的团聚效率随流速升高而降低的速率均逐渐减小,这可能是由于流速越大,流场内的湍动能耗散率越大,使得颗粒物停留时间对颗粒物团聚效果的影响减弱。 表2 不同流速下亚微米颗粒物数量浓度及团聚效率变化Table 2 Changes of concentrations and agglomeration efficiency under different flow velocities 不同流速下进出口压降变化如图8所示。进口流速升高会造成通道进出口压差升高,且升高速率随流速的升高而升高。随着进口流速升高,通道内流动阻力增大,影响湍流团聚效果,甚至影响烟气排放。因此实际应用中,需合理控制烟气流速。 图8 不同流速下进出口压降变化Fig.8 Variation of inlet and outlet pressure drop under different flow velocities 由于扰流件排布对流场影响很大,从而影响亚微米颗粒团聚特性。扰流件顺排布置与交错布置对流场与颗粒团聚效果的影响如图9所示。可知顺排对PM0.1与PM1的团聚效率分别为26.5%及18.9%,错排对PM0.1与PM1的团聚效率分别为28.4%及20.1%。PM0.1和PM1错排的团聚效率都大于顺排,两者团聚效率差距不大,但其对颗粒团聚的影响并不能简单从团聚效率角度来衡量。 图9 不同排布类型对应的团聚效率Fig.9 Agglomeration efficiency at different arrangement 顺排时的速度场与涡量场如图10所示,可知顺排中元件形成的尾涡会与其后面元件产涡发生耦合作用,使扰流件尾迹区的涡街充分发展,可以长距离携带小惯性颗粒,增加了湍流耗散率的有效距离。 图10 顺排时的速度场与涡量场Fig.10 Local distributions of velocity and vorcity in the aligned arrangements 扰流件交叉错排时的速度及涡量场如图11所示,可知错排结构使得颗粒更易撞击扰流件壁面,有助于颗粒横向移动并跟随涡流撞击下一个扰流件迎风面,增大团聚几率。但同时,错排结构中扰流件迎风面更易受到亚微米颗粒物的侵蚀,因此工业应用需要对这部分表面采用特殊处理以防止受到侵蚀。 图11 错排时的速度场与涡量场Fig.11 Local distributions of velocity and vorcity in the staggered arrangements 为探究扰流件形状对亚微米颗粒物团聚的影响,对3种形状的扰流件进行数值模拟。为节约计算成本,选取单个扰流件进行模拟计算,分析其对亚微米颗粒湍流团聚的影响。物理模型如图12所示。 图12 研究扰流件形状影响所用计算模型Fig.12 Calculation model used to study the influence of generator shape 扰流件形状分别为圆柱、三棱柱、Y型涡片。扰流件与进口之间的距离均为100 mm,通道长500 mm,宽高分别为100 mm与50 mm。网格划分采取结构化网格,总数约为120万。连续相与颗粒相所采用的模型与初始颗粒粒径分布以及计算参数均与前面计算相同,烟气进口流速为3 m/s。 不同扰流元件下颗粒团聚前后粒径分布如图13所示,采用Y型涡片作为扰流元件团聚效果最好,圆柱效果最差,主要原因是Y型元件产涡能力强,且圆柱对流场扰动能力弱,产生的湍流强度比较弱,使得湍流耗散率较低,导致颗粒碰撞几率降低。 图13 不同扰流元件下颗粒团聚前后粒径分布Fig.13 Particle size distribution before and after agglomeration under different generator element 3种形状扰流件的湍流耗散率场如图14所示,Y型涡片对流场作用产生的湍流耗散率最强,提高了颗粒的碰撞几率,且Y型涡片前端还有导流作用,尾迹区产生的漩涡固定性好,携带小颗粒能力强。而三角形扰流柱也可扰动产生可观的涡流,但其迎风面积比Y型涡片小,因此团聚效率相对较小。 图14 3种形状扰流件的湍流耗散率场Fig.14 Turbulent kinetic energy dissipation rate field of three kinds of generator 1)亚微米颗粒的团聚效率随颗粒粒径增大逐渐减小,粒径大于593.5 nm后团聚效率为负。团聚试验段的壁面效应以及亚微米颗粒的破碎等动力学行为不可忽视,相关机理模型有待进一步优化。 2)进口流速升高使得亚微米颗粒的团聚效率逐渐减小,虽然流速升高会使湍流耗散率升高,但同时颗粒在团聚段的停留时间变短,导致各组分颗粒浓度降低严重影响颗粒团聚效果,且流速过大会导致进出口压降过大,影响颗粒团聚及烟气排放。 3)3种扰流元件对亚微米颗粒物团聚效率从高到低分别是Y型涡片、三棱柱、圆柱。顺排和错排2种排布的团聚效率相差很小,顺排PM1团聚效率为18.9%,错排PM1团聚效率为20.1%,但其流场分布以及增强亚微米颗粒团聚的机理完全不同。在工业应用中应考虑材料磨损和颗粒沉积对运行的影响。1.5 数值计算设置
2 结果与讨论
2.1 数值模型验证
2.2 入口烟气流速的影响

2.3 扰流件排布对亚微米颗粒物团聚的影响
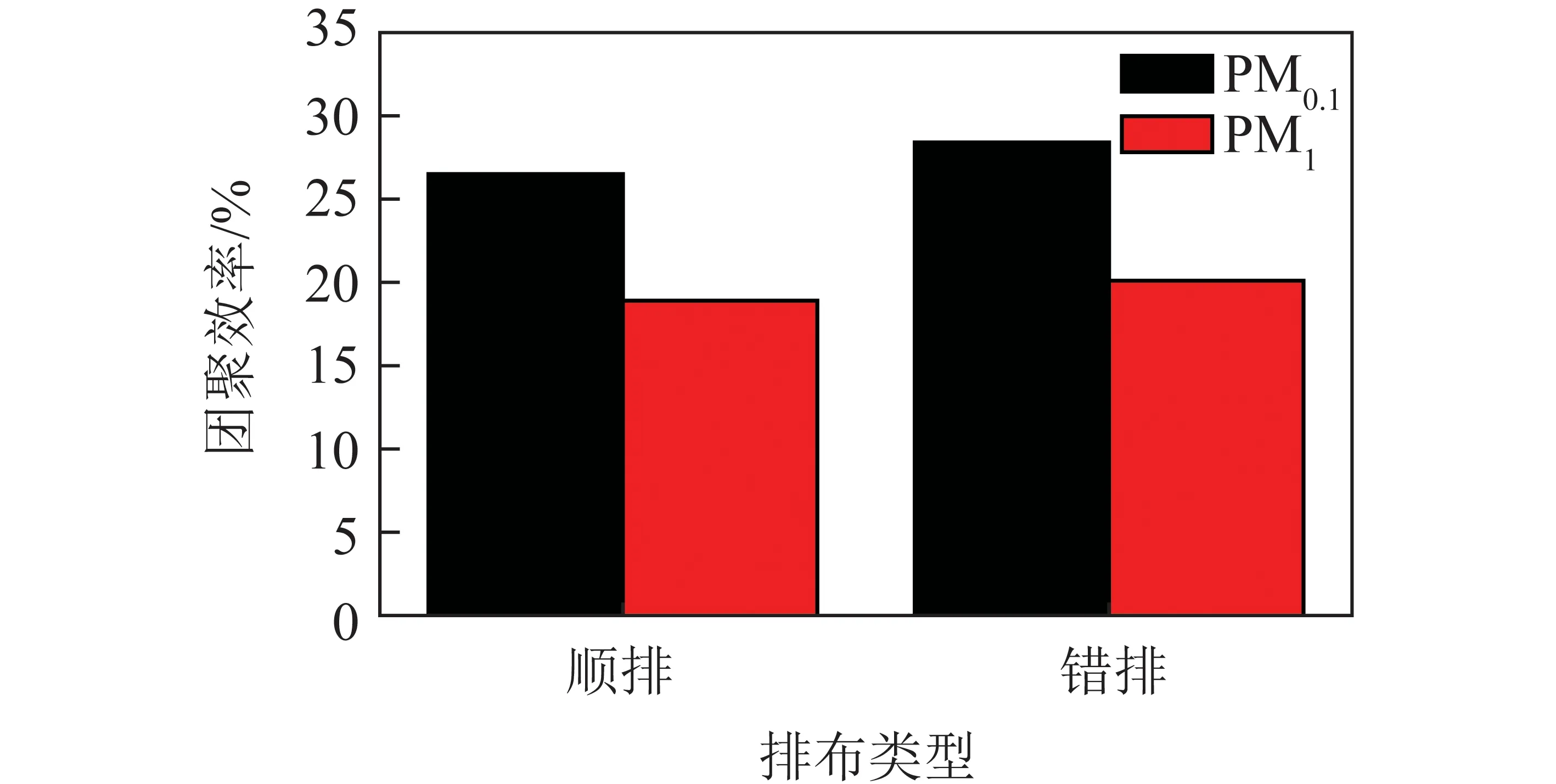
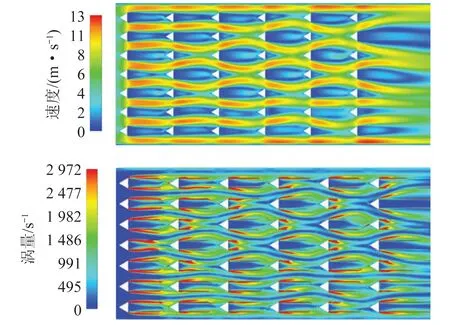
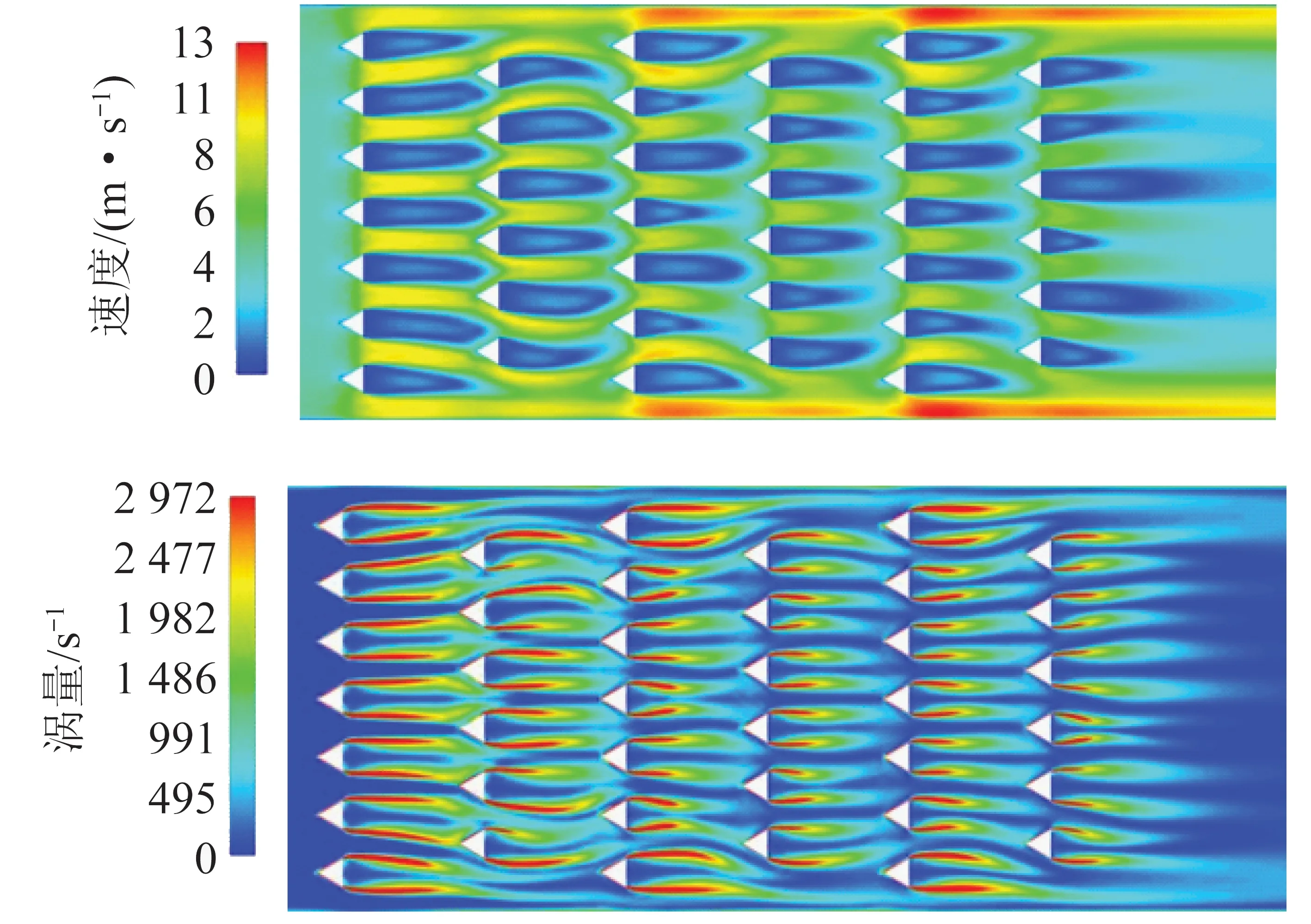
2.4 扰流件形状对颗粒团聚的影响


3 结 论

