压实机械对土壤应力的影响试验*

李博容，张志峰，倪 超，陈东方，谭凯明，王若飞

(1.长安大学 工程机械学院，陕西 西安 710064； 2.中航光电科技股份有限公司，河南 洛阳 471003)

0 引 言

土是一种松散的颗粒材料，土颗粒之间的接触强度相对软弱，容易发生相对滑移。振动压实过程中，由于土壤的塑性变形以及振动钢轮与土壤接触的不确定性，使两者的相互作用表现出复杂的非线性[1]。为此，不少学者一直致力于土壤压实特性的研究，并逐渐关注压实机械对土壤应力应变的影响[2-3]。Jude Liu和Radhey L. Kushwaha[4]在室内土槽中进行了振动压路机不同行驶速度、不同载荷和不同压实次数的作业工况下，土壤力和位移动态特性的试验研究，为土壤压实特性的研究与应用提供了试验支持。I S Tyuremnov[5]进行了振动压路机在各种工作模式下振动轮垂直振动的振幅和加速度试验，可以用于验证振动压路机在土壤压实过程中的数学模型，进而优化压路机参数和土壤压实模式。Michael A. Mooney和Robert V. Rinehart[6-7]通过将应力和应变传感器放置在垂直均匀和非均匀分层试验台的多个深度，研究了振动压路机在加载过程中土的应力应变特性，并将其与所测得的土壤刚度相关联，拟对土方工程质量进行评估。李晨光[8]针对压路机名义振幅、土壤压实度、铺层沉降量3个参数，对同吨位垂直振动压路机与圆周振动压路机的压实性能进行对比。陈世伟，郭健[9-10]基于地面力学的研究基础，对钢轮与地基相互作用力进行理论分析，并通过试验进行验证，可为优化压路机的振动参数以及提高现场施工质量提供理论依据。

振动压实过程中，土壤的竖向应力比较容易测得，在一定程度上可以间接反映土壤的压实特性。故为了探究不同深度处级配土的应力状态，进一步了解振动压实机理，笔者进行了级配土在低频高幅工况和高频低幅工况下的竖向应力测试试验。

1 试验准备

此次试验样机采用某22 t机械单驱单钢轮振动压路机，其基本参数见表1。试验参照GB/T18148-2015《土方机械压实机械压实性能试验方法》[11]及相关标准，制定样机在低频高幅和高频低幅工况下的振动压实试验方案，对级配土竖向应力进行测试。级配土虚铺厚度约为70 cm，并调整含水率为最佳含水率。

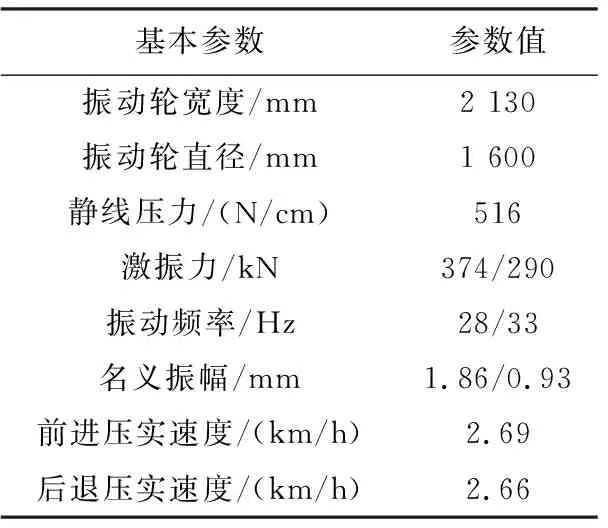
表1 试验样机压实性能参数

试验前先对级配土进行两遍静压，然后在距离土壤表面深度10 cm、20 cm、30 cm、40 cm和50 cm处布置应力传感器(如图1)，以采集振动压路机在压实过程中级配土的竖向应力。

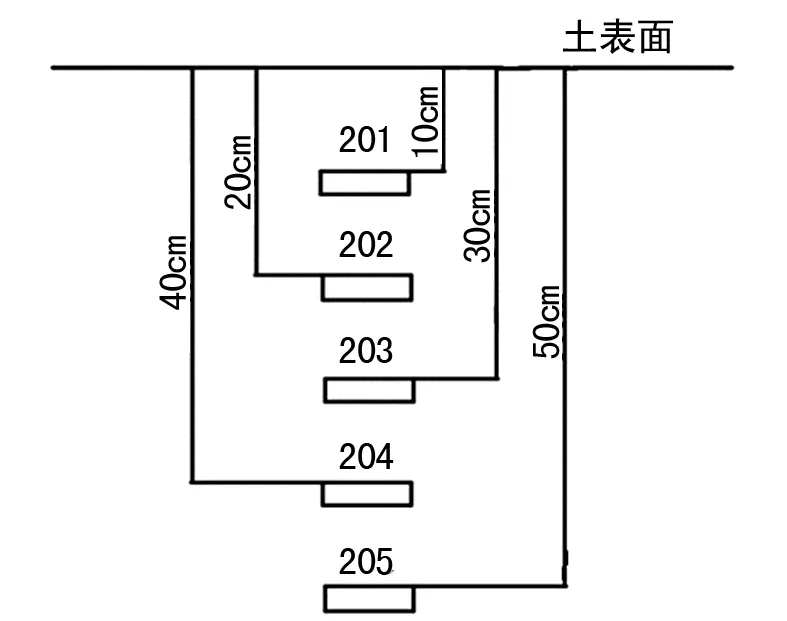
图1 传感器的布置位置

2 试验结果分析

2.1 低频高幅工况

本试验中样机以低频高幅工况进行12遍(前进6遍，后退6遍)压实作业，试验测得样机在级配土中以低频高幅工况匀速压实第3遍和第9遍10 cm层压应力时域和频域曲线分布规律如图2～3。

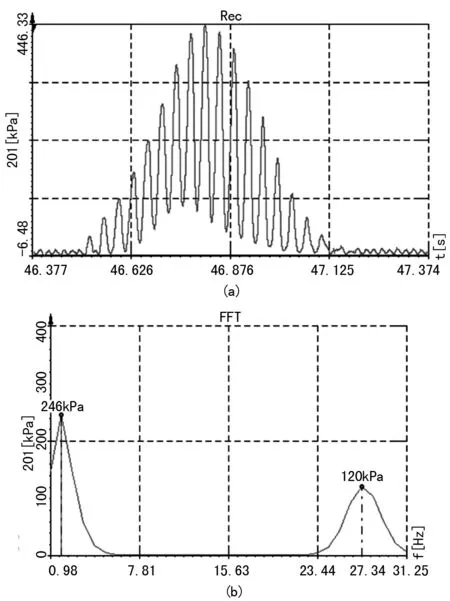
图2 10 cm处第3遍压实应力曲线及FFT曲线图

根据竖向应力时域曲线，在压实过程中，级配土的竖向应力总体呈现先增加后减少的抛物线型曲线。当振动轮靠近级配土下的应力传感器时，土壤的竖向应力开始增加；当振动轮处于传感器正上方时，土壤的竖向应力达到峰值；当振动钢轮远离传感器时，土壤竖向应力开始逐渐减小。

振动轮传递给土壤的有效作用力包括静态作用力和动态作用力，结合竖向应力频域曲线，土壤的竖向应力由两部分组成，即静态压应力和动态压应力[12-13]。由于在振动压实过程中振动轮振动加速度和激振力之间的相位角小于90°，导致激振力和振动轮的惯性力部分抵消，使得动态作用力比静态作用力小。故而在频域曲线中，静态应力值均大于动态应力值。振动压实的过程中，振动轮自身的重量对土壤的压实作用为一静态力(0.98 Hz处)，而激振力、振动轮和机架由振动产生的惯性力为一动态力(27.34 Hz处，与振动轮激振频率基本一致)。因此，被压实土壤受到静态压应力和动态压应力的共同作用。

压实过程中各个深度处应力传感器测试结果见表2。竖向应力幅值随压实深度变化曲线如图4，竖向应力幅值随压实遍数变化曲线如图5。

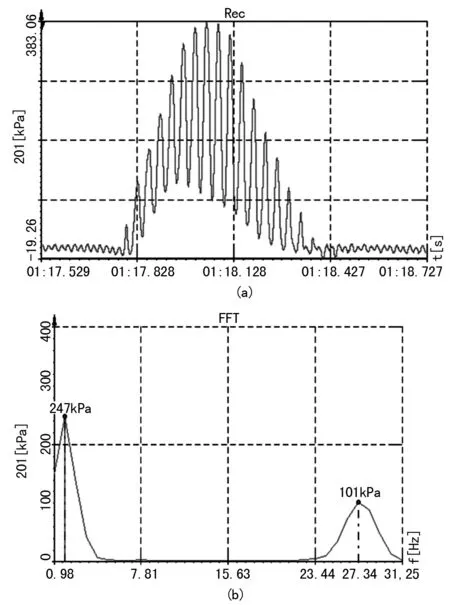
图3 10 cm处第9遍压实应力曲线及FFT曲线图

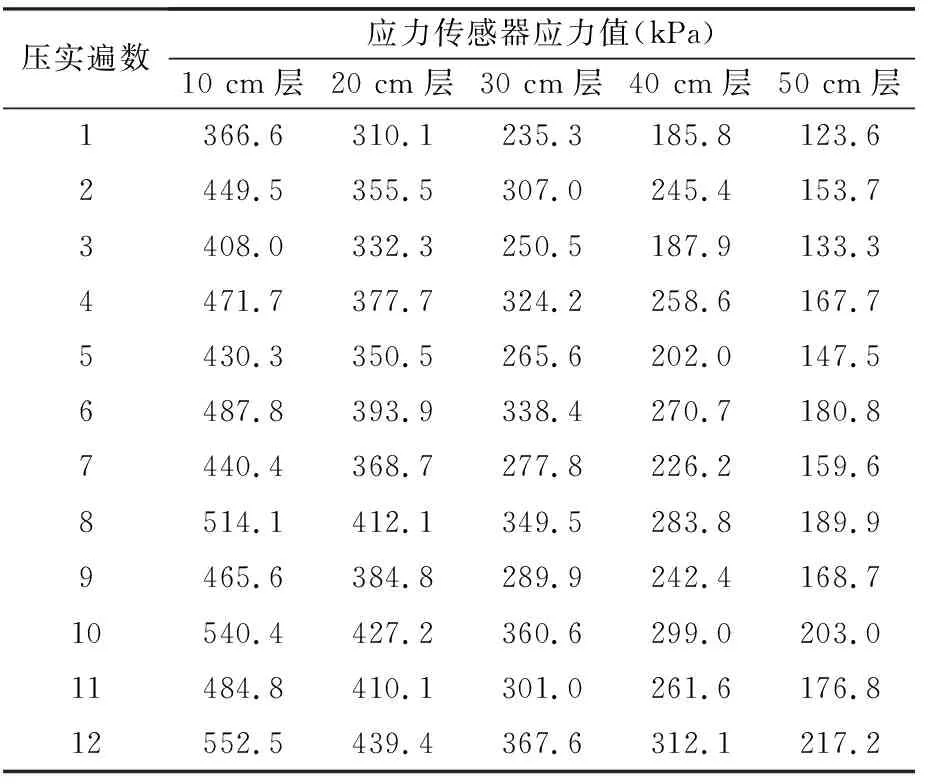
表2 不同深度处级配土的竖向应力值

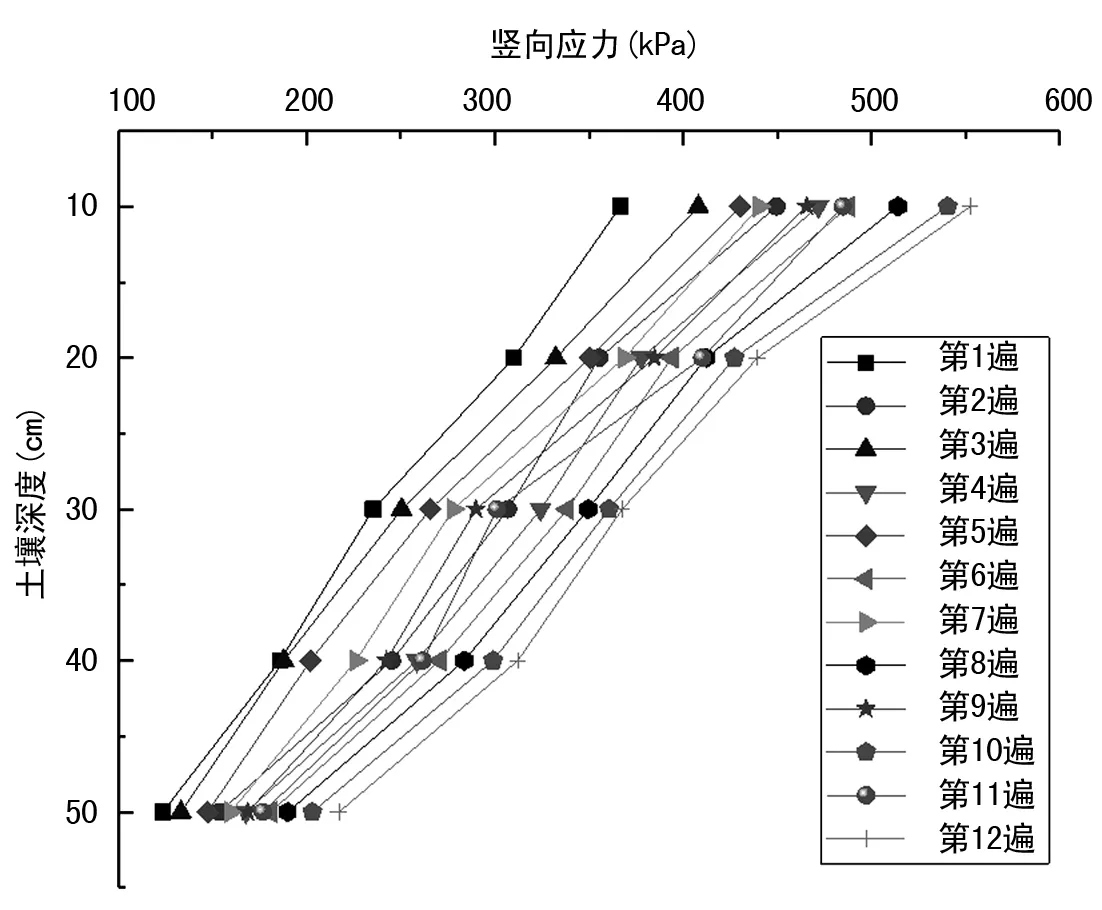
图4 竖向应力幅值随压实深度变化曲线

图5 竖向应力幅值随压实遍数变化曲线

综合图4、5，土壤的竖向应力值随着深度的增加而减小，曲线基本呈现一种线性衰减的趋势，其原因在于应力在土壤中的传播随深度的增加而衰减，衰减速度随深度的增加而减小。在同一深度处的竖向应力值随着压实遍数的增加呈现出锯齿状的增加趋势，其原因在于土壤在被压实的过程中，每遍压实都能使土壤的密实度增加，密实度的提高更有利于压力的传播。

且振动钢轮与土壤的接触面积减小，接触压力提高，使得不同深度处的测试应力值增加。曲线之所以呈现出锯齿状，是由于振动压路机在压实的过程中采用前进6遍、后退6遍的方式进行压实。前进压实的过程中，振动轴的旋转方向与钢轮的旋转方向一致，这就导致振动轮对土壤的最大作用力的位置发生一定的偏移，并不位于振动轮的正下方。故而与竖直方向存在一定夹角，作用力一大部分用于竖直方向的压实作用，另一小部分则用于对土壤的挤推作用。在后退压实的过程中，振动轴的旋转方向与钢轮的旋转方向相反，水平方向上的力可以进行一部分的抵消。此时振动轮给予土壤的应力或振动能量更多，压实的作用力位置更加靠近或位于振动轮的正下方，更有利于土壤的压实。

2.2 高频低幅工况

本试验中样机以高频低幅工况进行12遍(前进6遍，后退6遍)压实作业，试验测得样机在级配土中以高频低幅工况匀速压实第3遍和第9遍20 cm层压应力时域和频域曲线分布规律如图6、7。

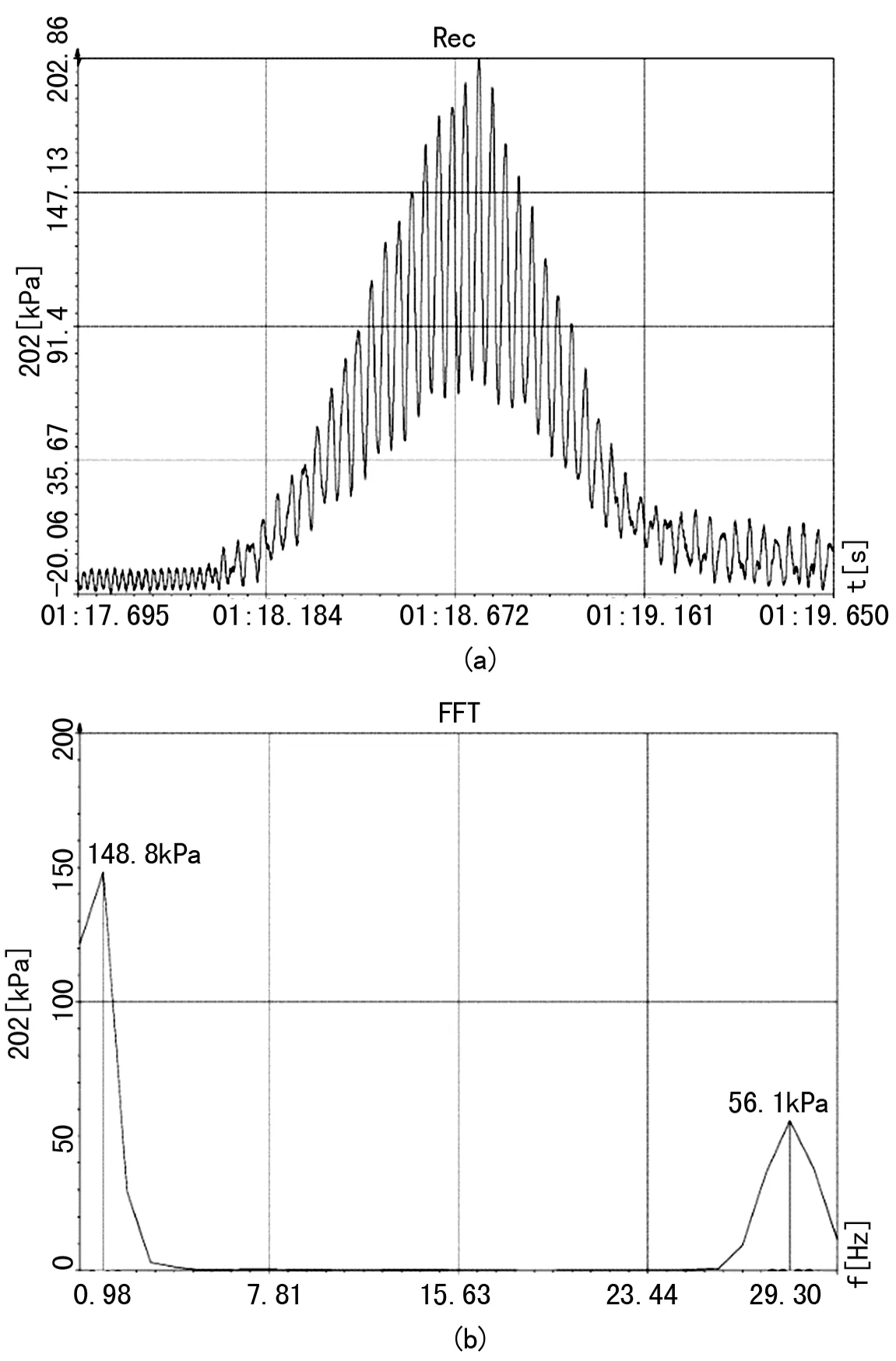
图6 20 cm处第3遍压实应力曲线及FFT曲线图

根据竖向应力时域曲线，在压实过程中，该工况下级配土的竖向应力与低频高幅工况下的应力分布规律基本一致，均呈现出先增加后减小的抛物线规律。根据竖向应力频域曲线，土壤的竖向应力亦由两部分组成，即静态压应力(0.98 Hz处)和动态压应力(29.30 Hz处，与振动轮激振频率基本一致)，同样静态应力值大于动态应力值。

图7 20 cm处第9遍压实应力曲线及FFT曲线图

压实过程中各个深度处应力传感器测试结果见表3。竖向应力幅值随压实深度变化曲线如图8，竖向应力幅值随压实遍数变化曲线如图9。

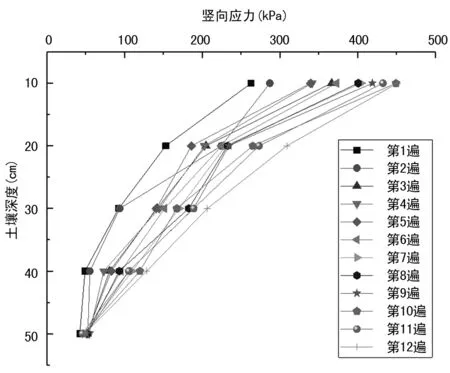
图8 竖向应力幅值随压实深度变化曲线

图9 竖向应力幅值随压实遍数变化曲线

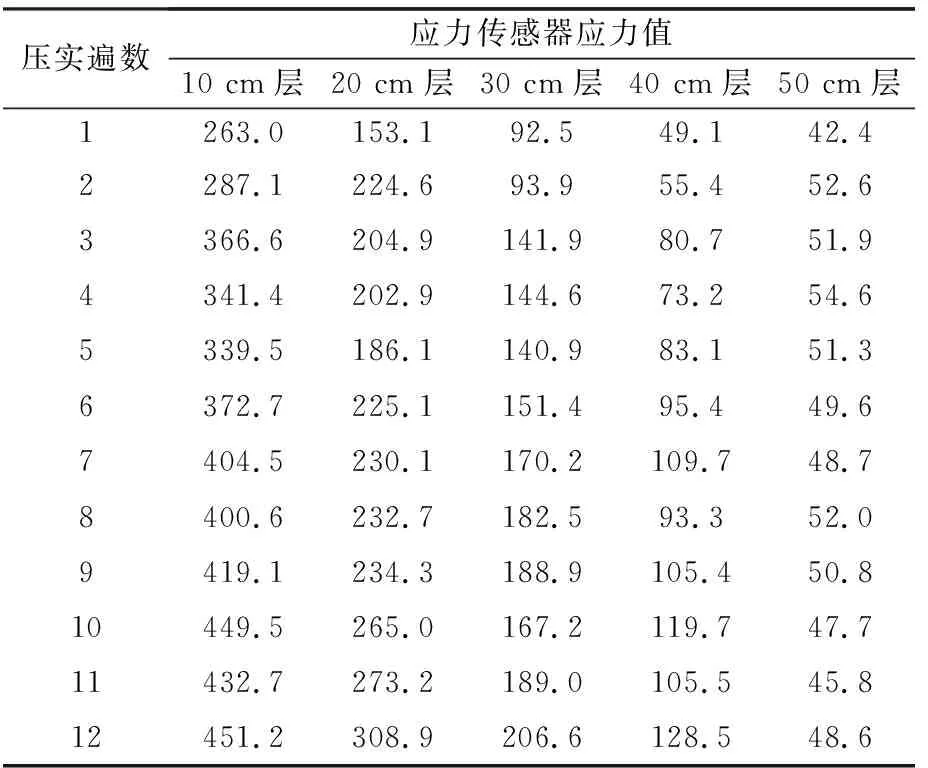
表3 不同深度处级配土的竖向应力值 /kPa

综合图8、9，土随着深度的增加，土壤竖向应力迅速减小，近似负幂函数规律进行衰减。同一深度处的竖向应力值随着压实遍数的增加而增大，浅层土壤处的竖向应力增加明显，随着深度的增加，竖向应力的增加逐渐趋于平缓。

2.3 不同工况下土壤竖向压力的对比分析

振动压实过程中，试验测得低频高幅和高频低幅工况下不同深度处土壤竖向应力在时域和频域的分布规律。根据时域曲线，级配土的竖向应力均呈现先增加后减少的抛物线型曲线，当振动轮处于传感器正上方时，土壤的竖向应力达到峰值。根据频域曲线，级配土所受的竖向压应力均由振动轮自重传递给土壤的静态压应力和激振力传递给土壤的动态压应力，且静态应力值大于动态应力值。

第三遍压实两工况各层深度的动态应力与静态应力值及其比值见表4。相同振幅下，随着深度的增加，动态应力与静态应力的比值逐渐增大，这说明动态应力对土壤的压实有较大的影响，动态应力对于级配土压实度的提高作用更加明显。同时，低频高幅工况动态应力与静态应力的比值明显高于频低幅工况，说明振动幅度对竖向应力影响较大，高幅工况下对级配土的压实效果更加显著。

表4 第3遍压实动态应力和静态应力值

对比图4和图8，土壤的竖向应力值均随着深度的增加而减小。但是，低频高幅工况曲线基本呈现一种线性衰减的趋势。而高频低幅工况曲线近似负幂函数规律进行衰减，其衰减速度明显快于低频高幅工况。说明高幅工况对级配土的压实更加深入，随着土壤压实度和刚度的提高，竖向应力可以作用到级配土更深层。对比图5和图9，同一深度处的竖向应力值随着压实遍数的增加均呈现增加趋势。但是对比高幅工况，高频低幅工况的竖向应力明显较小，级配土更深层的竖向应力增加逐渐平缓。在50 cm处，该工况下土壤竖向应力基本不发生变化。故激振力大小对竖向应力影响较大，高幅工况下对级配土的压实效果更显著。

3 结 论

通过试验对比分析了低频高幅和高频低幅工况下级配土中的竖向应力的分布规律，试验结果表明：

(1) 振动压实过程中，级配土的竖向应力总体呈现先增加后减少的抛物线型曲线，在顶点处竖向应力达到最大。

(2) 振动压实过程中，土壤的竖向应力由静态应力和动态应力构成，且静态应力幅值大于动态应力幅值，但是动态应力对土壤的压实度提高有较大的影响。

(3) 振动压实过程中，土壤的竖向应力值随着深度的增加而减小，同一深度处的竖向应力随着压实遍数的增加而增大。通过对比，采用低频高幅工况对土壤进行压实的效果更加显著。