金属弹簧管性能影响因素的仿真分析

常 健 李 华 蔡云丽 杨 磊 刘河洲

（1 上海交通大学材料科学与工程学院金属基复合材料国家重点实验室，上海 200240）

（2 中国运载火箭技术研究院，北京 100076）

（3 高新船舶与深海开发装备协同创新中心，上海 200240）

文 摘 为了研究高温密封组件金属弹簧性能，本文通过对波音公司编网状弹簧管结构和Streck 心脏支架结构的研究，建立了编织弹簧的几何拓扑构型和数学模型，推导了弹簧直径计算公式。采用AUTODESK 3D-MAX 构建了编织弹簧的仿真模型，用ANSYS 仿真软件分别从编织丝直径、编织密度以及编织方法3 方面探究不同测试对弹簧性能的影响。结果表明，增加弹簧丝直径、降低弹簧管轴向方向的编织密度、提高圆周方向的编织密度、向外的弹簧管编织方式可有效提高弹簧管的回弹性能。

0 引言

随着各国在太空领域研究热点的日益增加，各类超常规概念飞行器也层出不穷。虽然我国在高速飞行器研究取得一些瞩目进展，但用于航天飞机起落架舱门和轨道飞行器贮箱等飞行器的高温、高压的苛刻使用环境的耐高温柔性密封组件研究工作仍处于探索阶段［1］。美国NASA 和波音公司都曾做过很多关于高温密封的研究工作，如NASA-JSC（X-38项目）、NASA-ARC（热防护分支）、波音密封部门（X-38 项目）和Hi-Temp（密封和热防护制造）等［2］。为深化对金属弹簧设计参数的认知，更好地解决密封件与活动间隙的接触密封问题，本文参考波音公司MB0160—047 标准设计中编网状弹簧管结构和Streck 心脏支架结构特点，建立了一种编织弹簧的几何拓扑构型和数学模型，并用ANASYS 仿真分析了弹簧丝的直径、编织密度及编织方法对弹簧性能的影响，为后期的实物编织提供理论指导。

1 弹簧结构数学模型的建立

编织弹簧管为圆柱状空间立体几何结构。作为高速飞行器的关键密封组件，通过对波音公司MB0160-047 标准设计中编网状弹簧管结构的研究，结合Streck 心脏支架结构的技术特点，建立了图1所示的几何拓扑构型。Streck 弹簧管是由金属丝沿哑铃状轨迹线编织而成［3］。为了更直观地描述这种弹簧管而定义了弹簧管一系列的几何参数。这种针织结构可以利用两个与参数t 有关的路径函数进行描述，并且需要保证这两个函数分段处连续且光滑连接。公式（1）给出了这种针织曲线1/4［如图1（a）］的几何线段的函数方程，其他部分的图形［图1（b）］依次做镜像和阵列的形式进行构造。

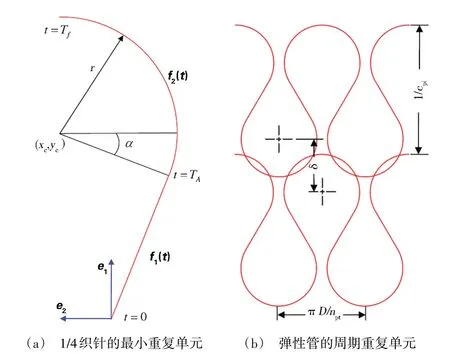
图1 MB0160-047规范的几何拓扑构型Fig.1 Geometric topology model of MB0160-047

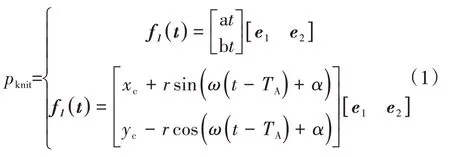
式中，f1表示针织状曲线的线性部分；f2表示针织状曲线的圆形部分；t为变化的参数；e1为与弹簧管轴向方向平行的矢量；e2为与弹簧管轴向垂直相切方向的矢量；a为f1中e1方向上的常数；b为f1中e2方向上的常数；TA为从f1至f2段的变量参数；Tf为在f2结尾处变量参数；xc、yc分别为在e1和e2方向针织状曲线圆形部分的圆心坐标；r为针织状曲线圆形部分半径；ω为定义关于变量参数t的针织状曲线圆形部分曲率值；α为圆分割处于1/4 圆处与圆心连线所成的角度；cpi弹簧管每延伸米所含有螺旋圈的个数；δ为两个最相邻针织状曲线圆心之间的距离；D为弹簧管的直径；npt为每圈上针织状曲线的个数。

为更好地描述每个针织状曲线圆心坐标xc、yc，它们的坐标将由以下形式给出：

对于参数Tf，其几何意义为1/4 针织状曲线终点位置的参数，它描述了这种针织状曲线轨迹沿着f2段终止的位置，它的关系可以表述为：

为了保证针织状曲线的连续性以及平滑，必须在圆以及线性处加以约束，使得这两处刚好相切，这种可以被以下5个方程进行定义：

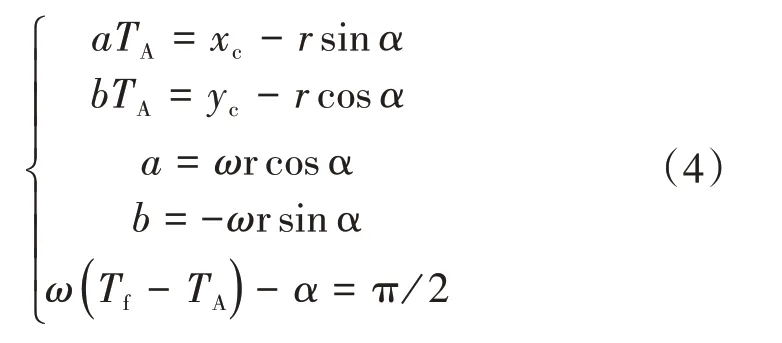
通过计算机带入参数t到函数中，求解出来的一系列的点就会沿着针织状曲线由t=0 位置到这种曲线尾端进行排列。弹簧管是金属丝沿着一个基本的螺旋线缠绕而成，这种螺旋线几何的曲线方程可以按下面函数进行表示：

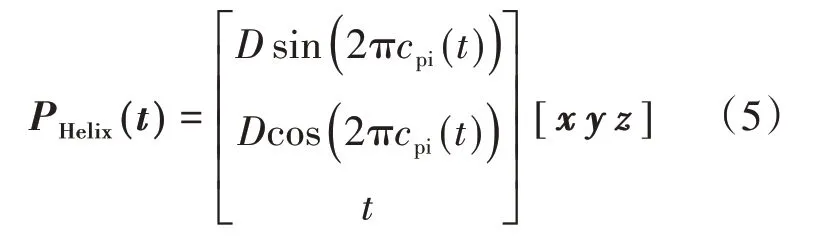
在基于螺旋结构PHelix(t)上曲线的每一点上的位置坐标系统都是由3个单位矢量构成，这种弹簧管的几何结构矢量的变化将按照式（6）进行。最后通过弯曲变形将笛卡尔坐标系的点投影到圆柱表面上，即最开始的1/4 的编制状曲线可以按下式进行计算：

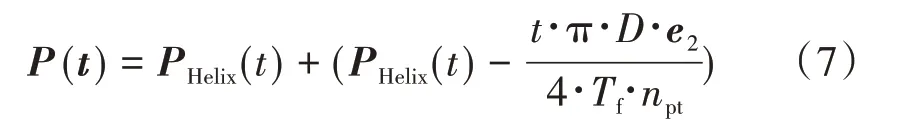
在本模型中，各个参数取值如表1所示。以模式一为例，根据弹簧的螺旋线特性，根据下式可推算弹性管直径D为15.67 mm。在确定上述参数后，可继续进行如下建模过程。

首先，做出弹簧最小织构单元［图2（a）］；然后根据式5做出螺旋的投影圆，并将其按照织构单元的重复数n等分。按照n等分圆节点构造单圈折线螺旋［图2（b）］，所得到的折线螺旋即最小织构单元所应处的位置；将最小织构单元排列在折线螺旋上［图2（c）］处理掉杂线并优化即得到弹性管的轨迹［图2（d）］；按轴向方向复制轨迹［图2（e）］即得到一般弹簧轨迹（图示为三螺旋）；最后沿轨迹扫掠即可得到弹性管模型［图2（f）］。

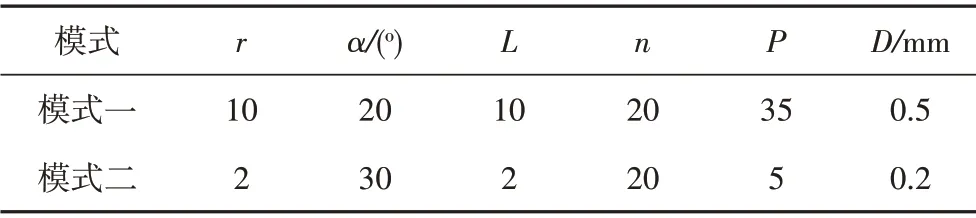
表1 弹性管参数Tab.1 Spring tube parameter

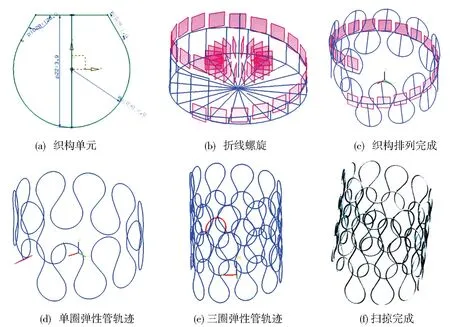
图2 建模过程Fig.2 Modeling process

2 编织弹簧结构参数的实物建模

利用Auto CAD 初步建立单个重复结构模型，即先将数学模型的轨迹曲线函数输入Auto CAD 中，再通过镜像和复制操作便可得到初步曲线。为模拟弹簧管丝间的交叠结构，需要对这种曲线结构进行调整，即在水平方向上使得曲线上下各翘起一个金属丝半径百分比的距离（本文分别为0.75D丝和0.25D丝）。经过以上调整，就可以建立一对具有交互关系的环状结构。之后，根据他们具有周期性柱状螺旋结构的特点，将它们进行弯曲和阵列，最终就得到了编网弹簧的几何状结构。

为节约计算机资源和减少计算量，在保证提高计算精度前提下尽量简化模型，本文主要做了以下简化工作［4］，简化后的弹簧管模型和弹簧管耦合连接后的效果分别如图3和图4所示。

（1）根据编网弹簧沿轴线方向呈周期性重复结构的特点，采用AUTODESK 3D-MAX 2012 建模，并将BEAM189梁单元赋予了弹簧骨架进行计算。

（2）考虑到在压缩加载时如果只是用一个压板对编网弹簧进行加载可能导致底部受力与实际偏差较大，于是便在弹簧管的上端与下端分别放置一个水平板。

（3）为了使得编网弹簧两端能够通过耦合作用以达到周期性结构弹簧管的受力效果，计算时将弹簧两侧的丝按节点耦合方式耦合在一起，使得它们等效于一个无限长的弹簧管。

（4）考虑到编网弹簧间的接触在模型建立中设置了两组接触对，分别为编网弹簧与上下板之间的接触以及编网弹簧丝之间的相互接触。上板与弹簧之间，弹簧丝与丝之间摩擦因数均为零。

图3 ANSYS中简化的弹簧管模型Fig.3 Simplified spring tube model in Ansys

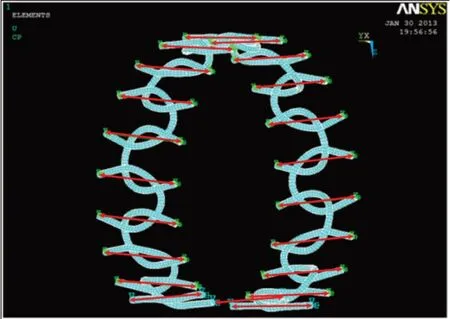
图4 简化的弹簧管耦合连接后的效果图Fig.4 Simplified effect diagram of coupling connection of the spring tube

加载时，上部压板在弹簧径向方向上加了大小为D弹簧/2 大小的位移载荷，并且约束加载板不能沿平行于轴向方向运动。下部压板保持不动，且为模拟弹簧管骨架实际使用环境，弹簧管与下部平板被设置足够大的摩擦力，使得弹簧管与板间不会发生相对滑动。图5为经过加载求解后得到的编网弹簧管50%变形后的应力分布云图，图6为编网弹簧撤掉50%形变加载后各处的位移情况。根据编网弹簧卸载后加载方向位移云图可以得到在加载方向最大位移为0.081，残余变形量为1.35%，满足现有工况要求。

图5 编网弹簧侧向50%形变加载后受力情况Fig.5 Force of braided spring under 50%lateral deformation loading

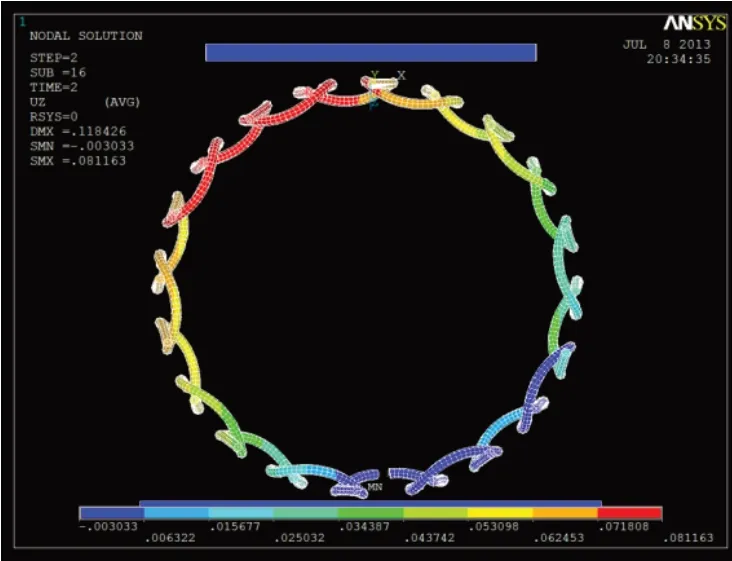
图6 编网弹簧撤掉50%形变加载后各处位移情况Fig.6 Displacement of the braided spring after removing 50%of deformation loading

3 编织弹簧性能影响因素分析

Streck 弹簧（以下简称编织弹簧）在力学性能方面展现了很强的力学性能优势［5］。为进一步探究优化Streck 弹簧的性能，本文分别从弹簧丝直径、编制密度以及编制方向这3 个方面来探究不同参数对Streck弹簧回弹性的影响。

3.1 弹簧丝直径对回弹性能的影响

本文共设计3 种具有相同Streck 密度、相同弹簧管径D弹簧管，弹簧丝直径Dw分别为0.15、0.20 和0.25 mm。从图7的模拟结果可以看出，弹簧刚度对线径非常敏感，且表现出非线性高次关系。若想提高弹簧管的回弹性能，增加线径将是一个有效途径。

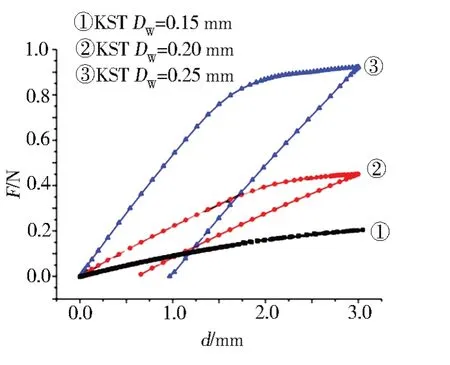
图7 弹簧丝直径对回弹性能的影响Fig.7 Influence of spring wire diameter on elasticity

3.2 弹簧的编织密度对回弹性能的影响

如图8所示，对于Streck 弹簧的编制密度分为轴方向和圆周方向。对此，本文分别设计了LL、LM、LS和Rn0.48、Rn0.59、Rn0.75 mm6种Streck弹簧，分别代表了在轴向方向与圆周方向编制密度的疏、中、密。

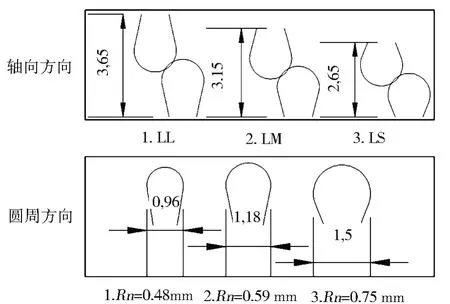
图8 轴、圆周方向具有不同密度的几种Streck弹簧Fig.8 Streck springs with different densities in axial and circumferential directions

在计算模型中，保持了此6 种弹簧管的直径、丝径大小相等，对于轴向三种LS、LM、LL确保它们之间的圆周密度相同，而对于Rn0.48、Rn0.59、Rn0.75 mm3 种模型则确保了它们之间轴向密度相同。从图9和图10可以看出，降低Streck 弹簧管轴向方向的编织密度、提高编织弹簧圆周方向的编织密度都可以提高Streck弹簧的回弹性。

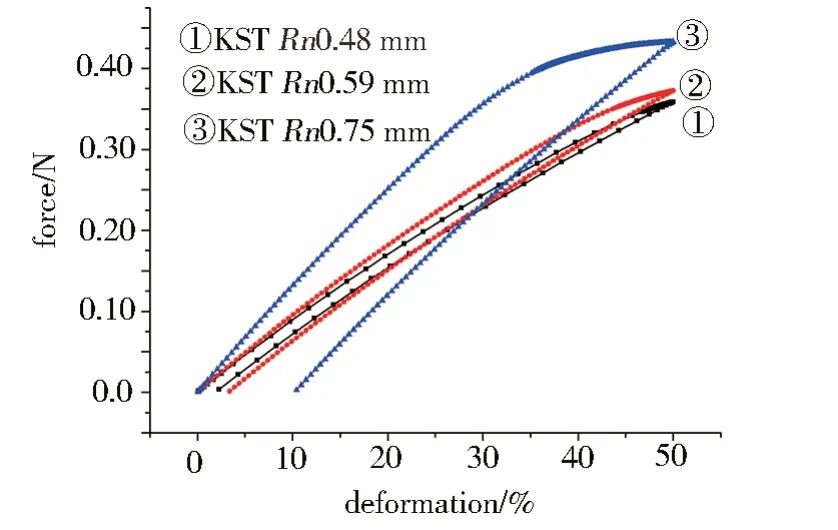
图9 圆周方向密度对回弹性的影响Fig.9 Influence of circumferential density on resilience energy

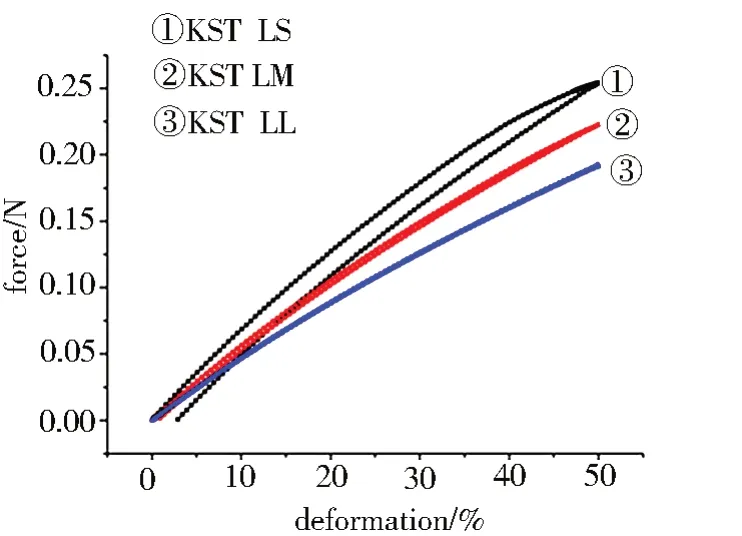
图10 轴向方向密度对回弹性的影响Fig.10 Influence of axial density on resilience energy

3.3 弹簧的编织方向对回弹性能的影响

如图11所示，在弹簧编制过程中，编织方向有两种方式：向外和向内。不同的编制方式，意味着在Streck 弹簧上的每个单元节变形方式有所变化。因此，建立编织弹簧-A、编织弹簧-B 两种模型对这种情况进行计算。如图12经过计算可以看出Streck 弹簧管的编织方向按编织弹簧-A方式编织将明显提高Streck弹簧的回弹性。

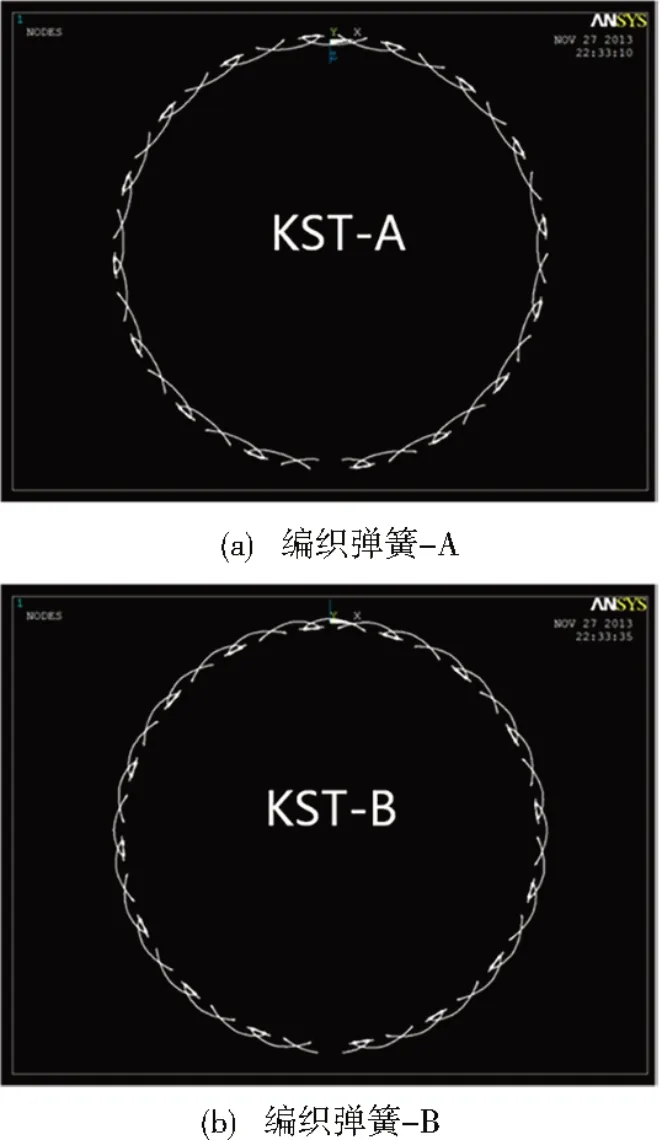
图11 具有不同编织方向Streck弹簧管Fig.11 Spring tubes with different braiding directions

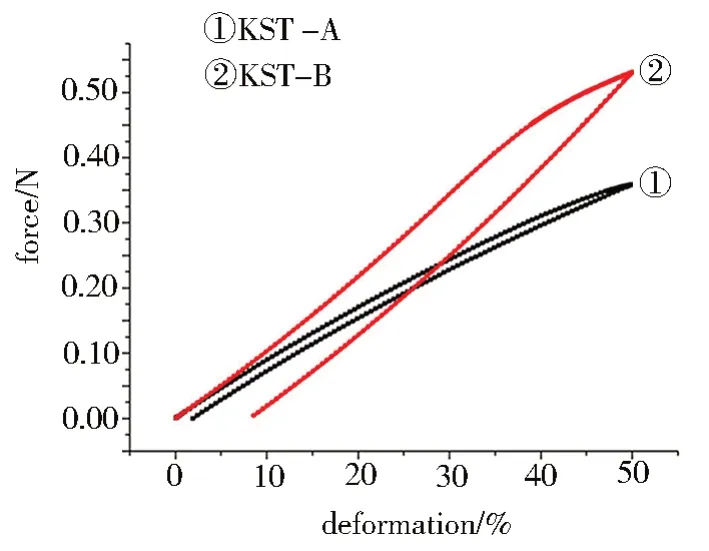
图12 编织弹簧-A、编织弹簧-B的回弹力-位移曲线Fig.12 Elasticity-displacement curve of the braided springs A and B

4 结论

本文参照MB0160-047 标准设计中编网状弹簧管结构和Streck心脏支架结构进行了参数化建模，采用AUTODESK 3D-MAX 2012 构建了编织弹簧的实物模型，并用Ansys计算了以下参数对弹簧管性能的影响，主要得到以下结论：

（1）弹簧丝直径与回弹力呈非线性高次关系，增加线径可有效提高弹簧管的回弹性能；

（2）降低Streck 弹簧管轴向方向的编织密度、提高编织弹簧圆周方向的编织密度都可以提高Streck弹簧的回弹性；

（3）向外的弹簧管编织方式将明显提高Streck弹簧的回弹性。