复杂地形下浙江夏季气候要素空间插值方法评价
张玮玮,张 眉,吴 杨,俞 布
(1.浙江省气象服务中心,浙江 杭州 310017;2.浙江省杭州市气象局,浙江 杭州 310051)
引 言
气温和降水的空间分布,在生态地理区域界线划定,陆面过程参数化,以及气象、水文模型参量设定等方面具有重要应用[1-4]。20世纪60年代随着地统计学方法的创立,提出了从样本自身统计特征和空间相对位置两方面来研究要素的空间插值特征的插值方法,如克里格插值、反距离加权插值、多项式内插法、径向函数法、Cressman法等,这些方法在站点分布密集、地势平坦区域的气象要素空间插值中得到广泛应用[5-7]。值得注意的是,传统地统计方法过分依赖样本空间密度,缺少气象要素演变机理,尤其对于地形复杂且站点分布不均的区域,气象要素空间插值的精度往往并不理想[8-9]。如在高海拔山区及地形起伏明显的山地丘陵区,由于台站稀少且分布不均,导致常规空间插值方法无法反映出气象要素随地形变化的空间变异特征[10-12]。
李新等[13]指出,没有绝对最优的空间内插方法,必须根据特定的环境区域选择最优的插值方法。20世纪90年代以来,以ANUSPLIN为代表的薄盘样条函数插值理论在气候数据曲面拟合方面引起关注[14],并在时间和空间尺度上得到应用。如谭剑波等[15]对青藏高原东南缘的气温要素进行空间插值分析,认为ANUSPLIN在山区气温模拟的细节方面具有优势;廖顺宝等[16]利用ANUSPLIN等5种空间插值模型对中国年平均气温空间插值结果进行误差分析,指出随着空间插值尺度的增大,误差增大的趋势也较为显著。综合表明,ANUSPLIN在气候数据空间插值方面具有较好的表现。但是,ANUSPLIN在地形复杂、地貌多样,梅雨期降水集中、台风影响明显的浙江地区是否仍具有精度优势值得进一步研究。本文选取地形起伏明显、海陆交界的浙江山地丘陵区作为研究区域。考虑受季风影响明显,浙江夏季高温,降水量约占全年40%,其中6—7月为浙中北梅雨期。此外,夏季受山谷风、海陆风等局地环流影响较多,对局地气温及降水影响明显。因此,利用ANUSPLIN对浙江夏季(6—8月)气温、降水数据进行空间插值分析,并通过交叉验证方法对比反距离插值和普通克里格的插值精度,探讨不同地形条件下插值精度的差异性与局地气候环境的关联性特征。
1 研究区概况与资料
1.1 研究区概况
中国东南沿海地区的浙江省(118°E—122.9°E、27.1°N—31.2°N),由西南向东北倾斜,地形复杂,北部是平坦的长江中下游平原区,中部以低海拔丘陵盆地为主,南部以较高海拔山地为主,东部为沿海丘陵、海岛及海洋区域,是检验插值方法适用性的理想区域。
1.2 数 据
选用研究区72个气象站点1988—2017年逐日气温、降水资料,数据来源于浙江省气象信息网络中心。参照王海军等[17]的方法进行数据质量控制,按照时间、空间和气候特征一致性原则,即极端数据需满足前后时间趋势一致、临近站点观测一致,符合季节气候特征等。剔除不连续数据、错误数据及冗余数据,确保数据质量和时间连续性,最终选用68个气象站点(图1)的日数据。统计各站点日数据,得出夏季平均气温和降水量,并参与空间插值。地形数据源于SRTM(shuttle radar topography mission)国际科学数据服务平台,空间分辨率为90 m,并利用ArcGIS重采样为100 m×100 m,并将高程数据转成ASCII格式,作为协变量参与空间插值运算。

图1 浙江省气象站点分布(阴影为海拔高度)Fig.1 The spatial distribution of meteorological stations in Zhejiang Province(the shaded for altitude)
2 研究方法
2.1 3种空间插值方法
局部薄盘光滑样条法ANUSPLIN(简称“ANU”)是基于局部薄盘光滑样条理论的统计模型[14],其在插值过程中利用最优的光滑参数实现逼真度和光滑度最佳平衡,保证了精度可靠,同时允许引入线性协变量子模型。本文在插值过程中引入了地形数据构建协变量模型。
反距离加权法(IDW)是根据站点间的距离确定权重进行插值,权重与距离成反比,离插值点越远的样本点,其赋予的权重越小[18]。普通克里格插值法(O-kriging)是地质统计中常用的插值方法。以区域化变量理论为基础,根据样本变异函数的类型选择合适的变异函数理论模型进行模拟,是对未采样点的区域化变量的取值进行线性无偏最优估计的一种方法[19]。
2.2 精度验证方法
采用交叉验证法[20-21]评价和比较不同插值方法的精度。交叉验证的基本原理是随机地抽取部分观测点,用其剩余的点来插值这些抽取的点,比较抽取点的实际观测值和预测值之间的误差,是评价插值方法优劣的一种方法。运用平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)评估插值方法效果。
从68个站点中每次随机选取20个点作为验证点,共取3次,得到60个验证点,计算3种插值方法验证点的MAE、MRE和RMSE,统计所有验证点误差直方图,并分析误差的空间分布。为了补充精度验证方法,充分对比3种方法的差异,将误差较小的两种空间插值方法得到的夏季均温和降水分别做差值,并对差异大的区域进行探讨和分析。
3 结果分析
3.1 插值结果比较
图2为ANU、IDW和O-kriging插值方法模拟的1988—2017年浙江省夏季平均气温空间分布。可以看出,3种方法均能客观反映浙江夏季平均气温的空间格局,其中ANU更能反映气温分布受地形影响的细节,如金华、丽水、绍兴为浙江平均气温高值区。IDW和O-kriging方法表现为区域性的普遍高值,夏季平均气温约27.5 ℃以上,如金华站(海拔64.7 m,夏季平均气温28.1 ℃)南北两侧及丽水站(海拔61.8 m,夏季平均气温28.2 ℃)东部平均海拔500~1000 m的高海拔山区,夏季平均气温仍为27.5~28 ℃。对流层内海拔高度平均每上升100 m,气温下降约0.65 ℃[22],金华站和丽水站附近海拔500~1000 m山区气温要下降3~5 ℃,ANU则对该地区的这一特征有所反映,夏季插值得到的平均气温为21~23 ℃。IDW和O-kriging的气温下限仅为25 ℃左右,而ANU的气温下限在17 ℃附近,主要分布在浙西南及浙北山区,符合气温随海拔高度升高而降低的观测事实。
图3为ANU、IDW和O-kriging插值方法模拟的1988—2017年浙江省夏季降水空间分布。可以看出,3种方法的空间分布总体一致,但不同于IDW和O-kriging方法,ANU对极端降水大值区的预测也有所体现。例如IDW和O-kriging对温州西南部泰顺地区的降水预测值均为800 mm左右,而ANU在此区域部分预测值超过850 mm,与泰顺站观测结果850.3 mm较为接近。从插值结果的细节来看,IDW存在“牛眼”现象,这是由于插值区域站点分布不均匀,插值过程中仅以距离为权重,易受站点极值影响,O-kriging插值通常较少出现“牛眼”现象。而ANU则利用控制点拟合成弯曲最小的曲面[14],能反映局部地形特征,并且有较好的平滑度。
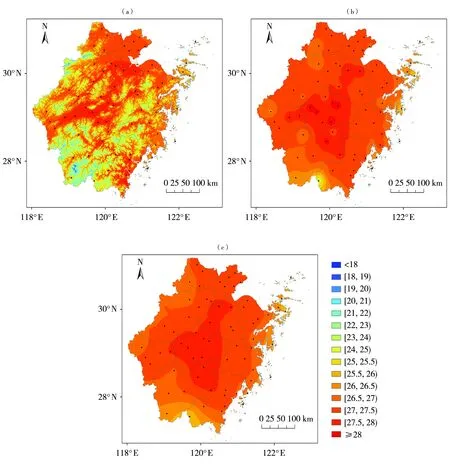
图2 基于ANU(a)、IDW(b)和O-kriging(c)插值方法模拟的1988—2017年浙江省夏季平均气温(单位:℃)空间分布Fig.2 The spatial distribution of simulated mean summer temperature (Unit: ℃) based on ANU (a), IDW (b) and O-kriging(c)interpolation methods in Zhejiang Province during 1988-2017
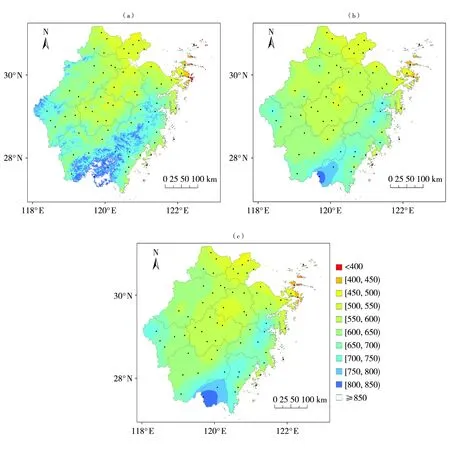
图3 基于ANU(a)、IDW(b)和O-kriging(c)插值方法模拟的1988—2017年浙江省夏季降水(单位:mm)空间分布Fig.3 The spatial distribution of the summer precipitation (Unit: mm) based on ANU (a), IDW (b) and O-kriging (c) interpolation methods in Zhejiang Province during 1988-2017
3.2 误差对比分析
3.2.1 交叉验证误差分析
无论是夏季平均气温还是降水量,研究区域ANU方法的MAE、MRE和RMSE均低于IDW和O-kriging,表明ANU方法的插值精度优于IDW和O-kriging。3种方法对夏季平均气温插值精度较为接近,MAE和RMSE均小于0.5 ℃,MRE仅为1.1%~1.2%,平均气温的可预测性较高,而对夏季降水量的插值误差均较大,其中MAE约为30 mm,RMSE约为40 mm(表1),主要原因可能是浙江夏季存在阶段性降水类型的差异。例如初夏时段(约6月上旬至7月上旬)浙中北地区受稳定性梅雨锋面影响,降水分布相对均匀,而浙南地区则以对流性降水为主,雨量分布相对分散;然而梅雨期结束后(约7月中旬至8月),浙江各地受副热带边缘气流影响,以热对流性降水为主。因此对于降水量而言,较难反映其插值误差规律,可预测性总体不高。
夏季平均气温观测值为24.8~28.3 ℃,其中ANU预测值(25.5~28.1 ℃,R2=0.62)与观测值较为接近,且明显优于IDW(26.4~27.9 ℃,R2=0.42)和O-kriging(25.8~27.9 ℃,R2=0.43)。夏季降水量观测值为397.8~850.3 mm,其中ANU预测值(396~763.9 mm,R2=0.82)仍然高于IDW(475.6~712.1 mm,R2=0.74)和O-kriging(435.8~756.6 mm,R2=0.79)插值,显然基于ANU方法的插值结果更接近观测值。总体而言ANU交叉验证点的预测值与观测值的拟合度均优于IDW和O-kriging(表2,图4)。

表1 基于3种插值方法的1988—2017年浙江省夏季平均气温及降水量预测值误差Tab.1 The error of simulated mean summer temperature and summer precipitationbased on three interpolation methods in Zhejiang Province during 1988-2017

表2 1988—2017年浙江省夏季平均气温和降水量观测值及基于3种插值方法的预测值的范围和均值Tab.2 The range and average of summer temperature and summer precipitation observed and simulated by three interpolation methods in Zhejiang Province during 1988-2017

图4 ANU(a、d)、IDW(b、e)和O-kriging(c、f)插值方法模拟的1988—2017年浙江省夏季平均气温(a、b、c)和夏季降水量(d、e、f)分别与其观测值的散点图Fig.4 The scatter plots between observation and simulated mean summer temperature (a, b, c) and summer precipitation (d, e, f) based on ANU (a, d), IDW (b, e) and O-kriging (c, f) interpolation methods in Zhejiang Province during 1988-2017
图5为基于ANU、IDW和O-kriging插值方法模拟的夏季平均气温和降水量的绝对误差频率直方图。可以看出,3种方法对平均气温预测均未出现较大误差,绝对误差集中在0.1~0.8 ℃,且小于0.3 ℃的站数约占60%。平均气温最大绝对误差为2.3 ℃,出现在基于IDW方法插值的泰顺站,泰顺站基于O-kriging方法的平均气温绝对误差为2.01 ℃,而基于ANU方法的平均气温绝对误差仅为0.68 ℃,可见ANU对夏季气温的预测存在精度优势。类似的,3种方法在夏季降水量预测中,绝对误差小于40 mm的站数占70%~80%,其中,基于ANU的MAE>50 mm的站点有8个,而基于IDW和O-kriging的站点分别为13个和12个,并主要表现为降水量低估。以泰顺站为例,该站降水量的绝对误差为60个检验站中最大,夏季降水量观测值为850.3 mm,基于IDW的预测结果为683 mm(绝对误差167.3 mm),基于O-kriging的预测结果为704.7 mm(绝对误差145.6 mm),而基于ANU的预测结果为753.6 mm,绝对误差仅为96.7 mm。
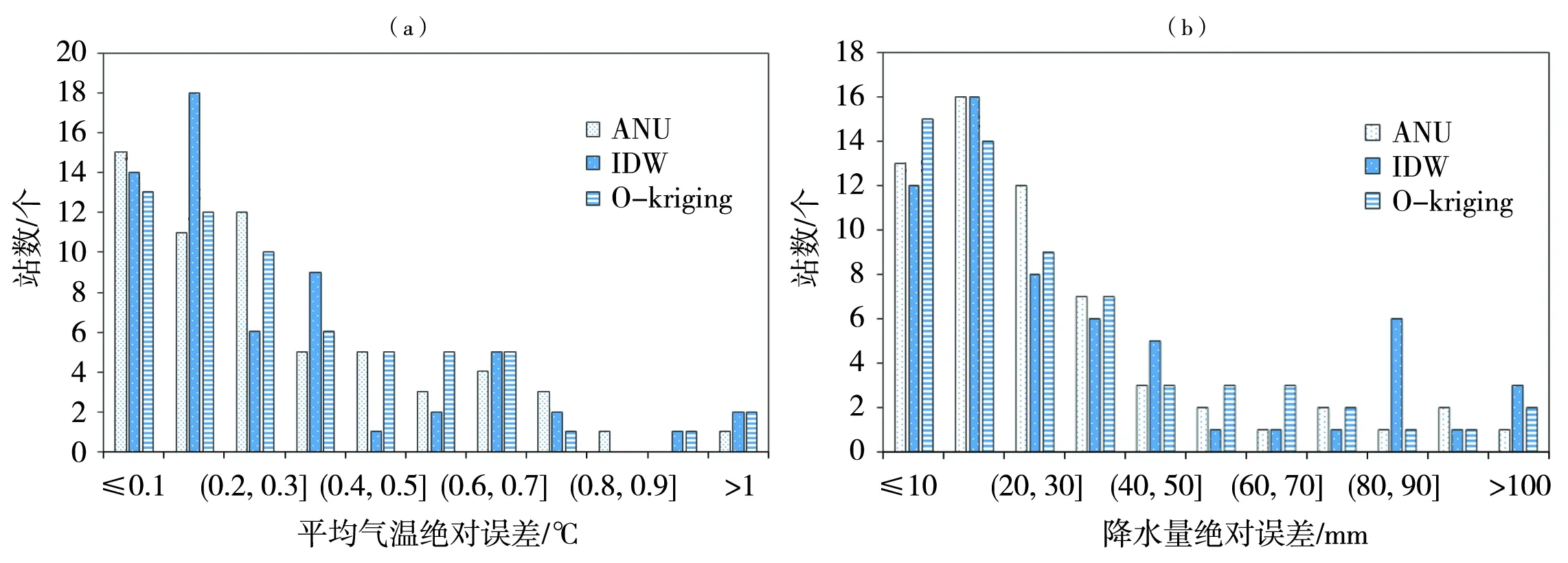
图5 基于ANU、IDW和O-kriging插值方法模拟的1988—2017年浙江夏季平均气温(a)和降水量(b)的绝对误差频率直方图Fig.5 The frequency histograms of absolute error of mean summer temperature (a) and summer precipitation (b) based on ANU, IDW and O-kriging interpolation methods in Zhejiang during 1988—2017
3.2.2 绝对误差空间分布
根据上述误差分析,IDW方法对平均气温和降水量的预测精度均低于O-kriging和ANU方法,因此在绝对误差空间分析中将不再考虑IDW方法。图6为基于ANUSPLIN和O-kriging插值方法模拟的夏季平均气温差值空间分布和60个验证站点夏季平均气温绝对误差柱状图。可以看出,在杭嘉湖平原、宁绍平原、东南沿海平原、中部金衢盆地地区,两种方法的插值较接近且其插值绝对误差均较小。而在浙南山地、浙西丘陵等地区,由于地形起伏大,气温变化梯度增大,两种方法的插值绝对误差均明显扩大,绝对误差差异达5 ℃以上,但ANU的插值精度优于O-kriging,且其对地形细节的描述更加精细。值得注意的是,武义、东阳、桐庐等地的ANU插值精度并不理想,这些站点主要位于干温河谷地带,平均气温较高,逆温明显,该区域海拔高低对气温的变化影响并不明显。而位于温州、平阳、玉环的浙江沿海地区站点也存在ANU预测值绝对误差增大的现象,这可能与沿海海陆风等局地环流对气温的调节作用有关。ANU高估区主要分布在沿海地区,受夏季海陆风气候调节作用,沿海地区的平均气温较内陆相同海拔高度地区明显偏低。而低估区一般在低丘河谷一带,由于夏季河谷地区白天辐射增温明显,空气流通不畅,有利于热量堆积,而夜间空气密度大,阻止地面长波辐射,加上河谷地区多为城镇聚集区,人为热排放较大并伴有焚风效应,增温机制复杂且热源多样。因此仅以高程为协变量的ANU方法还不能满足对该地区气温的精确预测,并容易造成平均气温低估。
图7为基于ANUSPLIN和O-kriging方法预测的夏季降水量差值空间分布和60个验证点夏季降水量绝对误差柱状图。可以看出,ANU和O-kriging两种方法的插值误差接近且空间分布规律较为一致。在沿海地区两者均表现为较大的绝对误差,这主要与沿海地区降水量偏多,降水空间异质性较大有关。ANU高估区主要分布在浙北湖州及浙中绍兴地区周边,而低估区主要分布在浙南温州一带,这与夏季降水的分布特征较为吻合,即降水量高估区域主要分布在降水量偏少的地区,而降水量低估区域主要分布在降水量相对较多的地区。两种方法插值结果相差较大的区域主要集中在山地区域,最大差值达236mm。ANU预测值大于O-kriging的区域主要位于高海拔区域,而小于O-kriging预测值的区域主要位于沿海及河谷地区。但总体而言,由于降水量与高程的相关性不如气温明显,即使在相似海拔高度的临近区域,两种插值方法的降水绝对误差亦呈现较大差异,此外,浙江夏季受对流性降水和台风降雨等极端降水影响,降水的空间异质性较大。因此,ANU对降水量的插值精度优势并不明显。
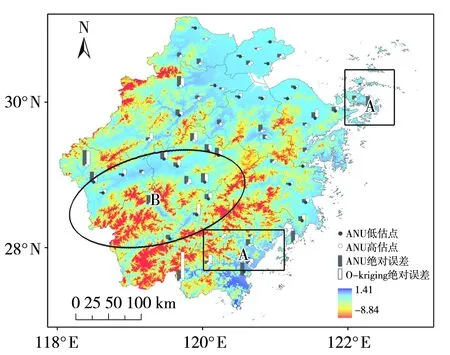
图6 基于ANU和O-kriging方法模拟的1988—2017年浙江夏季平均气温差值空间分布和60个验证站点夏季平均气温绝对误差柱状图(单位:℃)(柱状图中基于ANU和O-kriging的最大绝对误差分别为1.07 ℃和2.01 ℃,A、B分别代表ANU插值的夏季平均气温被高估和低估)Fig. 6 The spatial distribution of difference of simulated summer mean temperature based on ANU and O-kriging methods and the histogram of absolute error of summer mean temperature at 60 verification stations in Zhejiang during 1988-2017 (Unit: ℃)(The max absolute error in the histogram based on ANU and O-kriging methods were 1.07 ℃ and 2.01 ℃, respectively, A and B represent mean summer temperature overestimated and underestimated, respectively)

图7 基于ANU和O-kriging方法模拟的1988—2017年浙江夏季降水量的差值空间分布和60个验证点夏季降水量绝对误差柱状图(单位:mm)(柱状图中基于ANU和O-kriging的最大绝对误差分别为116.2 mm和145.6 mm,A、B分别代表ANU插值的夏季降水被高估和低估)Fig.7 The spatial distribution of difference of simulated summer precipitation based on ANU and O-kriging methods and the historgram of absolute error of summer precipitation at 60 verification stations in Zhejiang during 1988-2017 (Unit: mm)(The max absolute error in the histogram based on ANU and O-kriging were 116.2 mm and 145.6 mm, respectively, A and B represent summer precipitation overestimated and underestimated, respectively)
4 结论与讨论
(1)ANU、IDW和O-kriging 3种插值方法均能客观反映浙江夏季平均气温和降水的空间格局,夏季平均气温高值区域位于浙中的金华、绍兴等地,低值区主要在浙西南及浙北的高海拔地区;夏季降水大值区主要位于东南沿海和浙西地区,低值区位于浙北平原地区。但对于气象要素空间异质性大的区域,ANU方法因以高程为协变量,在细节上的表现明显优于IDW和O-kriging,且ANU有较好的平滑度。
(2)无论平均气温还是降水量,ANU的插值精度均高于IDW和O-kriging。平原地区平均气温插值误差总体低于山区且不同方法间的误差差异不大;而山地区域绝对误差明显增大,但ANU的插值精度仍有优势,且误差的高估点主要分布在沿海地区,低估点一般分布在山地和河谷。
(3)基于ANU与O-kriging方法预测的降水量绝对误差均相对较大,并主要集中在沿海地区。如ANU方法降水量高估区域主要分布在降水量偏少地区,低估区域主要分布在降水量相对较多地区,这与浙江夏季降水的空间分布特征较为一致。总体而言,由于降水量与高程的相关性不如气温明显,同一海拔区域站点的降雨量存在明显差异。在本研究区,ANU对研究区降水量的插值精度优势并不明显。
分别对基于3种插值方法模拟的气温和降水的研究比较发现,在误差精度和细节处理上ANU方法均较其他两种方法有优势,说明ANU方法在地形复杂的浙江地区进行气象要素格点化有较好的业务应用价值。
由于浙江沿海地区降水量偏多,降水空间异质性较大,降水较气温的不确定性大[23],且降水量与高程的相关性不及气温,另外夏季浙江受对流性降水多发和台风降雨影响,同一海拔区域站点的降雨量存在明显差异。因此,针对沿海地区插值效果较差,今后在降水插值方法中协变量可以增加距海岸线距离,从而进一步分析比较降水量插值效果。

