基于Melan解的地基变形计算分析研究

周 佺

(西南交通大学土木工程学院，四川成都 610031)

1 地基变形计算

在各类工程设计中，对地基土进行沉降计算时，其计算方法多数以太沙基一维固结理论为基础，假设地基土只产生竖向沉降位移，而忽略了水平位移，与实际工程情况不符。但随着我国经济的蓬勃发展，高层建筑、高速铁路、高速公路等工程的数量逐渐增多，规模不断扩大，对地基土变形的要求也变得更为严格。因此，如何准确地预测地基土在荷载作用下产生的变形就显得尤为重要[1-2]。

将岩土工程问题简化为弹性半无限空间问题或平面问题是解决相关岩土问题的一种常用方法，该方法可运用弹性理论解对地基土的变形进行预测。曾国熙[3]基于Boussinesq解推导了多种竖向荷载作用下泊松比为0.5的软黏土地基在弹性阶段的侧向位移理论公式。王华宁[4]利用对称性方法修正了Flamant位移解，给出了预测地表分布荷载作用下地基变形的沉陷公式。刘光秀[5]利用弹性理论解及平面应变问题给出了不同荷载类型下的地基侧向变形公式。

目前，学者们对地基变形的研究主要为作用在土体表面的荷载所引起的土体变形，而对作用在土体内部的荷载引起的地基变形研究相对较少。因此，本文在由弹性半无限平面内受竖向荷载作用的Melan应力解[6]推导Melan位移解的基础上，考虑竖向荷载作用下Melan位移解的镜面对称性，并利用弹性力学几何方程，确定位移解中的待定函数，推导出作用在土体内部的竖向荷载下的地基土变形解析解，且使得解析解在距离荷载作用点一定范围内收敛，并与有限元计算结果进行对比分析验证解析解的正确性。

2 Melan位移解推导

1932年，Melan在Mindlin解[7]的基础上，推导了弹性半无限平面内受线性荷载作用的应力解，即Melan应力解。本文在xy坐标系下，利用Melan应力解对竖向荷载作用下产生的Melan位移解进行推导，Melan解计算模型，如图1所示。

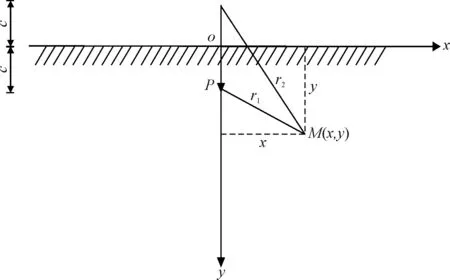
图1 Melan解计算模型

在弹性半无限平面内部作用竖向荷载时，在xy坐标系下，Melan应力解[8]为

(1)

(2)

(3)

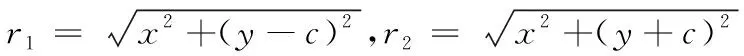
c为竖向线荷载作用深度；

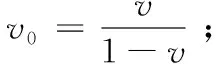
由弹性力学可得，平面应变问题中物理方程为

(4)

(5)

(6)

式中：εx为x方向正应变；

εy为y方向正应变；

γxy为剪应变；

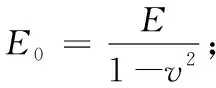
平面应变问题中的几何方程为

(7)

(8)

将式(4)、式(5)代入式(7)、式(8)中，则水平位移可表示为

(9)

则竖向位移的表达式为：

(10)

将Melan应力解式(1)、式(2)代入式(9)、式(10)中，可以得到弹性半无限平面内部c处受竖向荷载作用时产生的Melan位移解。

水平位移：

(11)

竖向位移：

(12)

式中：A(y)、B(x)为待定函数。

考虑Melan位移解在弹性半无限平面内受竖向荷载作用时具有镜面对称性，所以

u(-x,y)=-u(x,y)

(13)

w(-x,y)=w(x,y)

(14)

所以:

u(-x,y)+A(y)+u(x,y)+A(y)=0

(15)

因此，A(y)=0。

平面应变问题中几何方程为

(16)

其中

(17)

将式(11)、式(12)代入式(16)中，式(3)代入式(17)中，整理后得

(18)

所以，B(x)为常数，令B(x)=B。

Melan位移解表达式为:

(19)

(20)

当y=0时，则Melan位移解为：

(21)

(22)

可以看出，在y=0时，荷载在地表产生的水平位移随着水平距离x的增加而趋于一个定值，而竖向位移随着水平距离x的增加而增加，其位移值不收敛。

当x=0时，则Melan位移解为:

u=0

(23)

(5-2v0+v02)ln(y+c)2]+B

(24)

由以上推导可以发现，Melan竖向位移解是发散的，即位移计算点位置距离荷载作用点越远，Melan位移解计算结果越大，与实际岩土工程不符。王敏中[9]利用发散积分的有限部分将三维空间位移解简化为二维平面位移解得到了Melan位移解。王林中[10]指出对空间问题的相对位移求积，可解决在推导Melan位移解时由空间问题向平面问题积分而产生地发散积分问题。雷国辉[11]将Melan解析解、Flamant解析解与有限元分析计算结果进行对比分析，结果表明：在弹性半无限平面内及平面边界面上，线荷载作用方向产生的相对位移解答不收敛且具有多值性，并认为将岩土工程问题作为半空间问题分析更为合理。

因此，为了使得Melan竖向位移解收敛，并考虑在实际土木工程中，由荷载作用引起的位移只会在距离作用点一定范围内产生。因此，本文考虑当x=0时，在距离原点一定位置处，即y=y0，w=0，代入式(24)中，由此得解得：

v0)ln((y0-c)2)-(5-2v0+v02)ln((y0+c)2)]

(25)

y0可根据岩土工程条件和荷载作用大小进行确定。

所以，Melan位移解为:

(26)

(27)

3 算例

为验证求得的地基变形解析解的正确性，本文将解析解的计算结果与ABAQUS有限元模拟的计算结果进行对比分析。

有限元ABAQUS计算模型，如图2所示。计算参数如下：竖向集中力为P=100kN，集中力作用深度c=10m，弹性模量E=30MPa，泊松比v=0.3，y0=100m。在模型的左右边界设置水平和竖向位移约束，在模型下边界设置竖向位移约束。

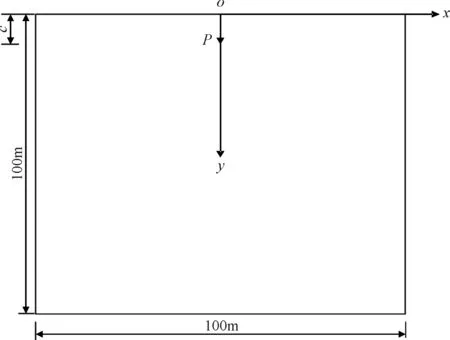
图2 有限元计算模型

3.1 地基水平变形

如图3所示，为解析解和有限元分析在水平距离荷载作用点2 m和10 m位置处地基土的水平变形分布曲线。

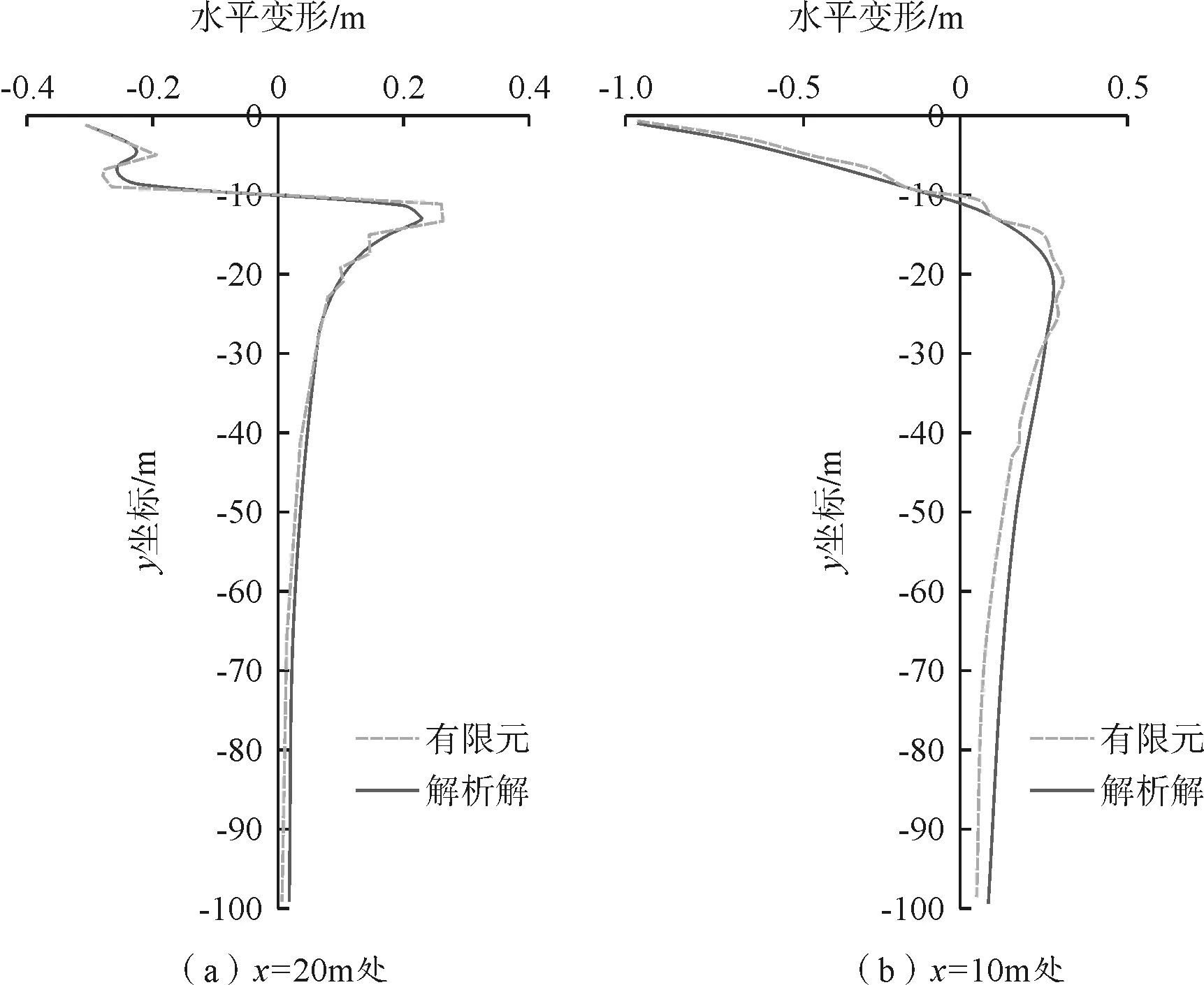
图3 水平位移分布曲线

由图3可以看出，解析解得到的计算结果和有限元分析的计算结果基本一致，吻合较好。

3.2 地基竖向变形

如图4所示，为解析解和有限元分析在距离地表0 m、10 m、20 m和40 m深度处地基土的竖向变形分布曲线。

图4 竖向位移分布曲线

由图4可以发现，解析解得到的计算结果和有限元分析的计算结果基本一致，吻合较好，且在水平距离荷载作用点50 m(y0/2)位置处竖向位移趋于零，即地基土竖向变形在该范围内收敛。距离地表越远，地基土变形解析解和有限元分析的计算结果越接近，分布曲线越吻合；距离地表越近，分布曲线吻合度下降。这是因为距离地表越近，所受约束越少，对变形计算结果影响较大。

4 结束语

本文结合弹性力学物理方程和几何方程，利用Melan应力解推导了Melan位移解，并在考虑Melan位移解受竖向荷 载作用时镜面对称性的基础上，确定了Melan位移解中的待定函数，推导出基于Melan解的弹性半无限平面内受竖向荷载作用的地基变形解析解，并使得解析解在距离荷载作用点一定范围内收敛。通过对有限元ABAQUS分析计算结果与解析解的计算结果进行对比分析，结果表明，解析解计算结果与有限元分析计算结果基本一致，吻合性较好，验证了解析解的正确性。