地震作用下跨断层隧道位移响应滞后特性研究

唐浪洲，杜明哲

(1.中铁四院集团广州设计院有限公司，广东广州 510600；2. 西南交通大学交通隧道工程教育部重点实验室，四川成都 610031)

随着西部大开发全方面的深入和开展，我国交通领域建设迎来了前所未有的挑战。尤其在川藏铁路全面规划建设过程中，许多长大铁路隧道不可避免地穿越位于活跃地震区的断层带。而2008年汶川地震后的震害调查结果表明，跨断层隧道受地震破坏尤为严重[1-3]。由此可见，对地震作用下跨断层隧道的位移响应进行研究十分重要。

迄今为止已有许多研究人员对此进行了相应的研究。安俊吉等[4]采用数值模拟的方法首先研究了在因断层粘滑而造成的地表位移下隧道结构的动力响应特性。胡辉等[5]设计了一种既能模拟断层自主震动又可以保持隧道穿越活动断层时的纵向振动响应性质的模型实验装置。Yang,Zhihua等[6]采用三维离散元模型，结合汶川地震地震动的实际记录数据，对隧道-断层系统的动力响应特性进行了研究。隋传毅等[7]通过相似模型振动试验研究了三种隧道结构的动力特性和破坏类型。孙风伯等[8]基于震害调查结果，着重研究了隧道破坏受破碎带垂直距离的影响，并在此基础上对其相关性进行了归纳。唐垠斐[9]依托摩岗岭隧道工程，通过相关实验及现场测试，利用有限差分数值方法，对穿越破碎断层的隧道结构的动力响应规律和抗减震技术展开了研究。孙风伯等[10]分析了分段隧道在断层作用下的变形特性，在此基础上确定了在该情况下隧道组合抗震缝定量计算公式。王峥峥[11]对跨断层隧道展开了相似模型振动台试验，得到了设置隧道抗震层的减震效果。信春雷等[12]基于相似模型振动试验，研究了隧道结构地震动加速度响应、应变反应及震后破坏状态，并对其减震措施展开了深入研究。Anastasopoulos,Ioannis等[13]基于非线性有限元模型研究了准静态断层在厚层覆岩中的传播规律及其与沉管隧道的相互作用。Corigliano,Mirko等[14]采用有限元模拟的方法研究了穿越活动断层的深埋隧道在三维地震波场条件下的土体和结构作用特性。Ichimura,T等[15]为了研究地震作用下断层-结构体系，提出了一种基于多尺度的分析方法，并某长大公路隧道为例验证了该方法的有效性。

目前国内外研究主要集中在山岭隧道跨断层带的破坏特性及抗减震技术的研究，而对于地震时隧道的瞬变动力特性的研究较少。由于穿越断层隧道在我国交通隧道中数量众多，而地震灾害又往往是瞬间发生。因此研究跨断层隧道的地震瞬变现象十分必要。本文首先通过对穿越垂直断层隧道的振动响应进行理论推导，提出了在地震发生瞬间，断层区域隧道的位移响应滞后时间，即地震时跨断层隧道位移响应首次峰值出现时间与地震波首次峰值时间之差，并推导了位移瞬变响应滞后时间的计算公式。然后结合数值模拟研究了地震时跨断层隧道位移响应滞后效应与断层无阻尼固有频率的关系，验证了推导结果的正确性。最后通过改变衬砌刚度进一步研究了跨断层隧道位移瞬变响应的变化规律。论文的研究思路和结论对今后高烈度地震区跨断层隧道的抗震及避险设计有一定的参考价值。

1 计算模型及理论推导

在本节首先以垂直断层为研究对象，地震波由下向上垂直输入，故位于断层中部隧道结构的竖向位移可假设为与断层质心位移一致。因而研究断层中部隧道结构的位移响应转变为研究断层质心的位移响应。在本节仅对无衬砌模型进行理论分析。如图1所示，k1、c1分别是左侧围岩对断层的切向刚度和切向阻尼，k2、c2分别是右侧围岩对断层的切向刚度和切向阻尼。F(t)为地震动激励力，x(t)为断层质心的位移响应。

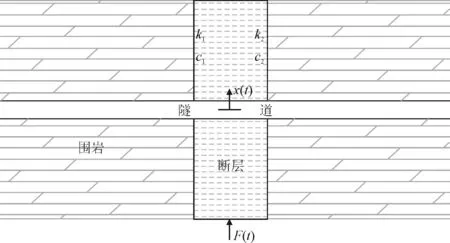
图1 跨断层隧道理论分析模型

由于断层两侧的围岩一般岩石坚固，并与大地连为一体，因此可以把断层两侧的围岩视为相对静止的参照物。所以，取断层为隔离体，其振动微分方程为[16-17]：

(1)

式中：m为断层质量，t为时间。

而断层两侧的围岩的物理性质应该是相同的，所以有c1=c2和k1=k2，上式变为：

(1)

设F(t)为关于时间t的简谐函数，则解振动微分方程式(2)可得：

x(t)=e-ξωnt{[-X(0)+x(0)]}cosωdt+

(3)

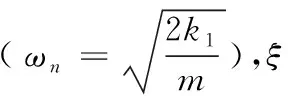
对于本文模型，初始位移和和初始速度应该为零。因此，将(3)式中初始位移和和初始速度取零，可得：

(4)

式(4)中，前一项为瞬态响应，其变化十分复杂且在较短的时间内逐渐消失；后一项为稳态响应，其变化较为简单且只要地震动继续进行就不会消失。为进一步分析稳态响应和瞬态响应的关系，令瞬态响应为Xn(t)，地震动激励力F(t)=F0sinωt(ω为激励力频率，F0为激励力振幅)，则稳态响应为：

X(t)=X0sin(ωt-φ)

(5)

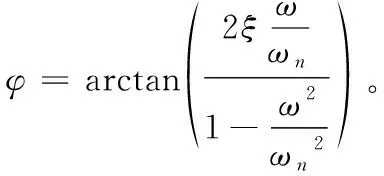
(6)

Xn(t)=X0e-ξωnt(Acosωdt+Bsinωdt)

=X0e-ξωntCsin(ωdt+φ1)=X0e-ξωntCsin(ωdt-φ2)

(7)

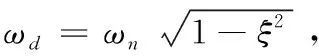
(8)

(9)

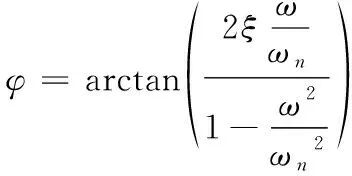
(10)

因而，对于瞬态响应相位差φ2，有：

(11)

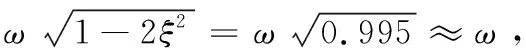
同时对于稳态响应相位差φ，有：

(12)

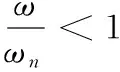
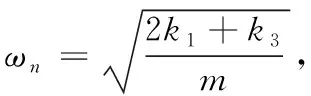
2 数值计算模型及力学参数

2.1 数值计算模型

为了保证隧道数值计算结果的可靠性，尽量消除边界效应的影响，隧道计算模型水平方向长度取66 m，沿隧道纵向取55 m，模型高度为66 m，断层宽5 m(图2)。数值模拟模型分为有衬砌和无衬砌两种，每种各有四种工况。其中隧道衬砌厚度为30 cm。隧道围岩、衬砌均采用实体单元模拟，其中围岩采用摩尔-库伦模型，二次衬砌则采用弹性本构模型计算。

地震加速度波取用简谐波，其变化函数为f(t)=2πcos(20πt)，通过将加速度波转化为应力形式，从模型底部垂直向上输入并乘以0.5的系数进行折减。模型底部使用粘弹性边界，四周为自由边界。

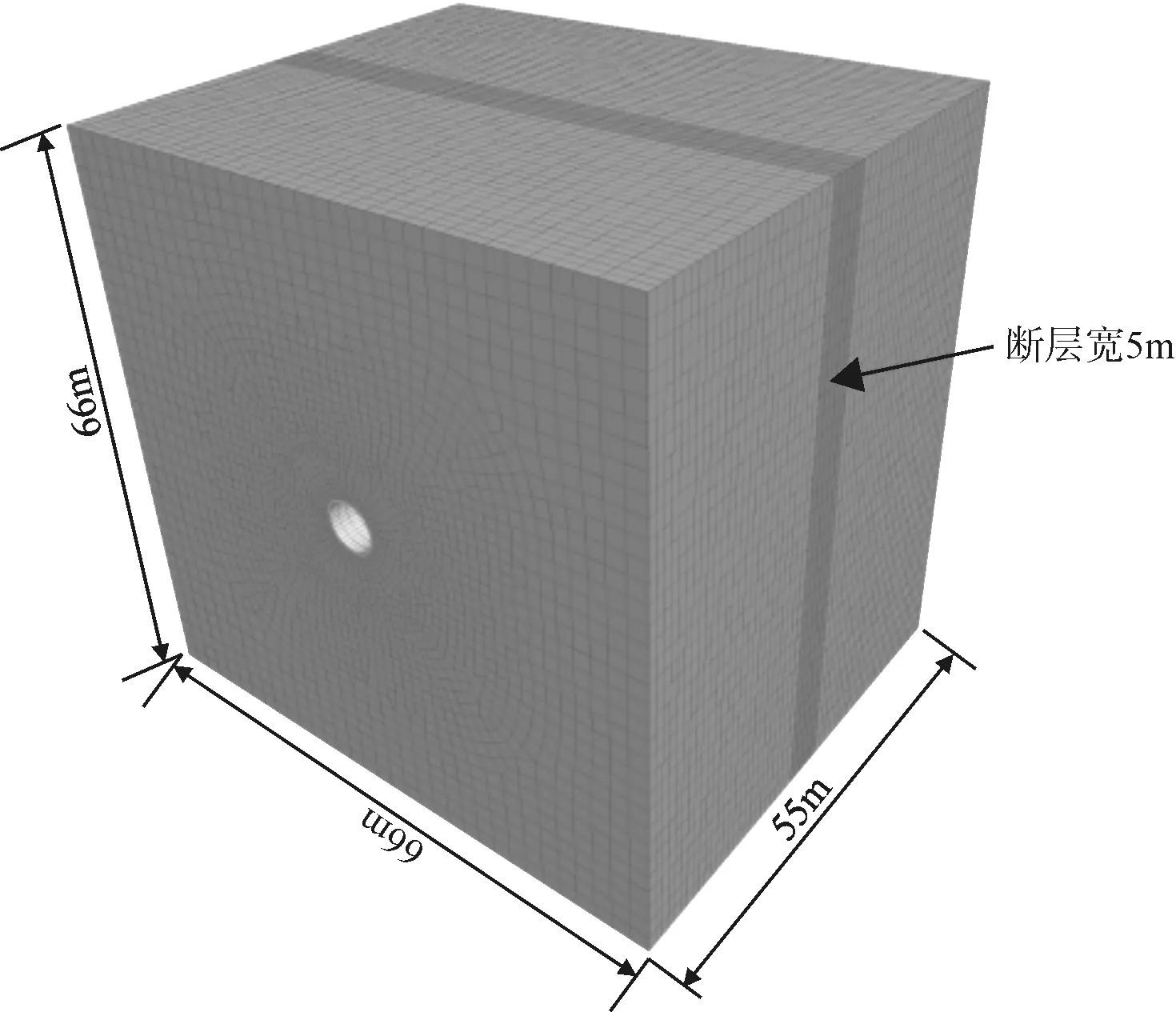
图2 隧道数值模拟模型

2.2 数值计算力学参数

本文采用FLAC3D软件来求解围岩与隧道衬砌结构的动力力学作用关系。数值模拟阻尼模块选用为局部阻尼，临界阻尼比为5 %，即局部阻尼系数为0.157。

在本节，研究有无衬砌两种情况下，跨断层隧道断层中部位移响应滞后特性，其中有衬砌和无衬砌隧道计算模型下各自对应四种工况。计算选取的物理力学参数指标与各工况参数分别如表1～表3所示：

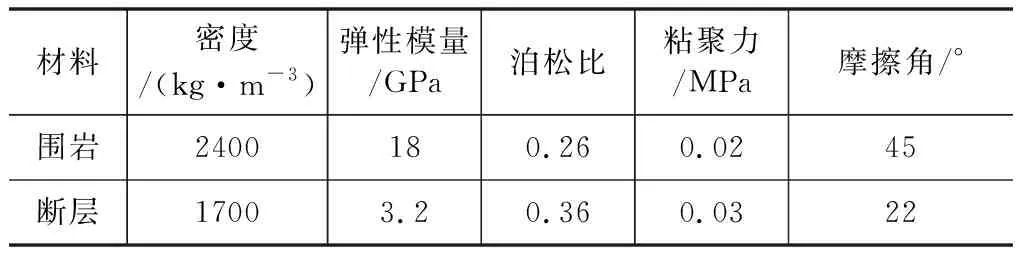
表1 隧道围岩与断层物理力学参数指标

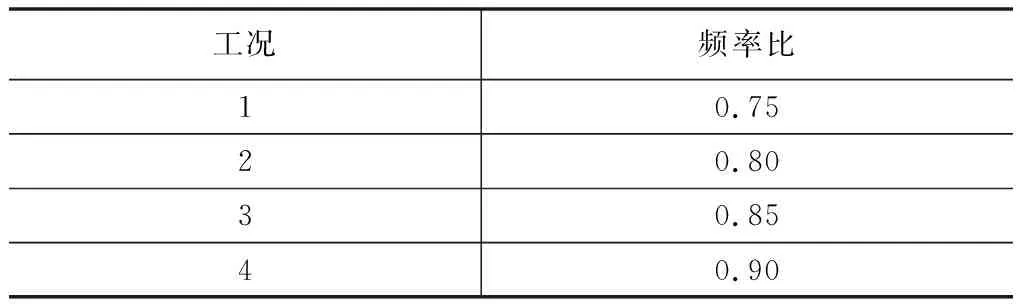
表2 无衬砌隧道计算模型工况一览

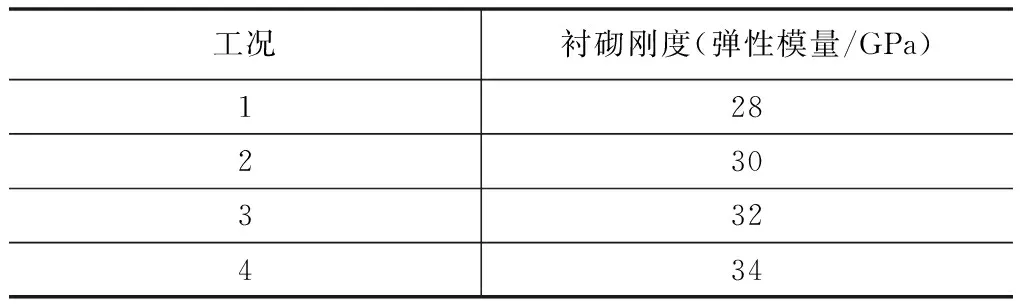
表3 有衬砌隧道计算模型工况一览

3 结果分析

3.1 无衬砌不同频率比下位移响应规律

为排除动力计算中重力造成的影响，故取隧道在断层中心拱腰处的垂直位移进行研究。在四种不同频率比工况下，位移响应时程曲线如图3所示。

图3 无衬砌隧道不同频率比下位移响应曲线

从图3可以看出，在无衬砌隧道结构下，由于四种工况的频率比不同，位移响应峰值首次出现的时间不同。工况一频率比为0.75，在0.499 s时出现位移响应峰值；工况二频率比为0.8，在0.051 2 s出现位移响应峰值；工况三频率比为0.85，在0.052 1 s时出现位移响应峰值；工况四频率比为0.9，在0.053 0 s时出现位移响应峰值。因此，对于跨断层隧道在地震作用下，在地震波输入频率小于断层无阻尼固有频率且地震波输入频率不变时，断层无阻尼固有频率越大隧道响应位移滞后效应越小。

3.2 有衬砌不同刚度下位移响应规律

隧道在四种不同衬砌刚度下，隧道断层中心处的垂直位移随地震动时间的响应变化如图4所示。

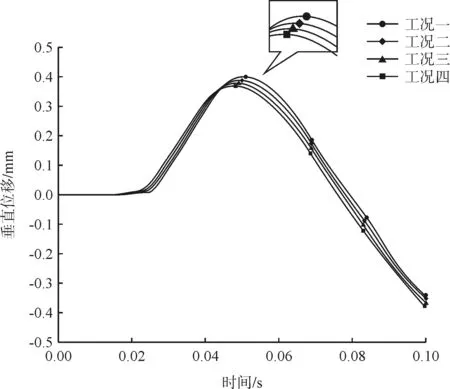
图4 有衬砌隧道不同刚度下位移响应曲线

从图4可以看出，在有衬砌隧道结构下，由四种工况的衬砌刚度不同，位移响应峰值出现时间不同。工况一隧道衬砌刚度为28 GPa，在0.050 7 s时出现位移响应峰值；工况二隧道衬砌刚度为30 GPa，在0.049 6 s时出现位移响应峰值；工况三隧道衬砌刚度为32 GPa，在0.048 5 s时出现位移响应峰值；工况四隧道衬砌刚度为34 GPa，在0.047 4 s时出现位移响应峰值。因此，对于跨断层隧道在地震作用下，有衬砌隧道随着衬砌刚度(弹性模量)的增加，隧道响应位移滞后效应逐渐减小。

4 结论

本文通过建立跨断层隧道理论分析模型利用振动力学理论推导了位移响应滞后时间的计算公式，得出了位移滞后时间与断层固有频率的关系并通过数值模拟实验验证了理论推导结果的正确性和有效性。主要得出以下结论：

(1)在地震波的输入频率与断层无阻尼固有频率比小于1的情况下，固有频率越小，隧道位移响应滞后效应越明显。

(2)对于跨断层隧道结构而言，则可以通过降低衬砌刚度，以降低无阻尼固有频率，从而增加隧道位移响应滞后效应。

本文通过对穿越垂直断层的隧道进行振动力学的理论推导首次提出了隧道在断层区域的位移响应滞后时间，并结合简单的数值模拟在一定程度上验证了推导结果的正确性。但本文取用了差别较小的值，数值计算出的结果相差并不大，因此该理论需要在后续的工作中进一步地研究和完善。本文的研究思路及成果对今后的高烈度地震区跨断层隧道的抗震避险设计有一定的参考。