带钢表面粗糙度自适应滤波检测技术研究
汤文杰,瞿海霞,牟战旗
(宝山钢铁股份有限公司1.冷轧厂,上海 201900; 2.中央研究院,上海 201999)
高端汽车外板涂装后需要具有高的鲜映性、光泽度和成像清晰度,其涂装质量除受涂漆工艺本身影响外,汽车外板表面形貌亦是重要影响因素[1]。因此表面形貌是冷轧带钢的重要表面质量指标。一般评定表面轮廓的重要指标分别是表征宏观几何形状误差、中间几何形状误差和微观几何形状误差的形状误差、波纹度和表面粗糙度[2-3]。其中表面粗糙度对于冷轧板而言至关重要,能直接影响钢板的冲压成形与金属的流动特性,是冷轧产品质量的重要的指标之一[4-5]。因此在冷轧带钢生产过程中需要对带钢表面粗糙度进行监控。
当前冷轧带钢生产中所采用检测方式是,在冷轧后处理机组出口(如连续热镀锌机组或平整机组)处,对带钢进行抽检取样,然后在实验室对样板进行离线测试获取带钢的表面粗糙度参数,并与下游用户的技术要求进行比较。如果带钢表面粗糙度不满足下游用户的要求,则在后续生产计划中对同类带钢的生产工艺参数进行必要调整;然后再抽检取样、离线分析测试、在线调整工艺参数等,直到带钢的表面粗糙度完全满足下游用户要求为止。但是该方法具有滞后性和非连续性,且取样部位一般在头部和尾部,无法代表整块钢板的粗糙度。
随着技术的不断进步,表面检测技术得到了迅速的发展,主要可以划分为以针触法为代表的接触式检测技术和非接触式检测技术[6-8],其中非接触式检测技术又可以划分为光学法和原子力检测法[9-10],光学法又可以划分为干涉法、散射法、散斑法、光学触针法、衍射法、光纤传感法等[11]。接触式检测方法得到的测量结果可靠,但是容易损伤测试样品表面并且磨损测头[12],因此限制了接触式检测仪器在表面检测中的应用。虽然原子力法检测的精度更高,但原子力法检测中探针与被测表面的间距非常小,不适合用于冷轧带钢表面粗糙度的检测。相比之下以光学效应为基础的光散射法,具备检测速度快、检测范围宽、抗干扰性好、体积小易于集成的特点,在表面粗糙度在线测量的理论研究与工程应用方面得到广泛关注与实践。德国EMG自动化公司开发的SORM 3plus系统,应用散射法,实现在不与带钢接触的情况下测量运动中冷轧带钢的表面粗糙度,国内外已有50多条机组安装SORM 3plus系统,已部分实现代替离线取样检测[13]。
散射法实现无损在线检测带钢表面粗糙度的关键技术之一是滤波算法,由传感器检测得到的原始的表面轮廓信号中包含形状误差、波纹度及表面粗糙度的信息,此外原始信号中还包含噪声和许多与被测量无关的干扰信号[14]。因此,为了能从测量获得的初始检测信号中快速准确辨识出带钢表面粗糙度参数,我们需要对原始信号进行滤波处理。现有滤波算法主要采用高通滤波法[15-16],虽然快速性好,但参数检测的准确性和精度因高通滤波器的单一滤波条件限制而很难提升,寻求快速性好、准确度高的滤波算法成为拓展散射法带钢表面粗糙度在线检测应用的瓶颈所在。而高精度的自适应滤波技术越来越受到重视[17-18]。
为了解决散射法中带钢表面粗糙度在线检测传统滤波方法的不足,本文研究适合冷轧带钢表面粗糙度在线检测的回归平滑自适应滤波方法,以提升带钢表面粗糙度参数辨识的准确度。
1 检测系统原理与构成
1.1 检测原理
高精度的滤波方法包括按照某种结构设计的滤波器和与之配套的算法。
随着技术的发展,滤波器分为经典滤波器和现代滤波器两大类。经典滤波器是先预制不同信号的频带信息,进而有效去除无用信息,因此无法去除与有用信号频谱重叠的噪声信号;现代滤波器是在无任何预制信息的情况下,将原始信号中所有信号均视为随机信号,之后利用它们的统计特征,导出有用信号的最佳估计算法,并用硬件或软件实现[19]。本文中即采用现代滤波器,并研究与之配套的自适应滤波方法。该滤波方法的滤波频率是自动适应输入信号而变化的,即利用前一时刻获得的带钢表面参数信息,自动调节现时刻的滤波参数,以实现有用信号与噪声随机变化的统计特性,从而实现最优滤波。这样的自适应滤波方法,更适合冷轧带钢粗糙度的实时在线测量。
在线检测带钢表面粗糙度时,所检测原始信号的统计特征未知,自适应滤波方法能自动调整自身参数以满足最佳准则要求;根据不同的准则,产生不同的自适应算法,最主要的两种基本算法是最小均方误差算法和递推最小二乘算法[20]。本研究中采用最小二乘算法。自适应滤波基本原理为,输入信号x(n)通过参数可调的数字滤波器后产生输出信号y(n),将输出信号y(n)与标准信号d(n)进行比较,得到误差信号e(n)。e(n)和x(n)通过自适应算法对滤波器的参数进行调整,之后反复迭代计算,直至误差信号e(n)最小。
1.2 检测流程与设备
表面粗糙度在线检测回归平滑自适应滤波方法设计如图1所示,将来自光源的光经过光纤送入调制器,然后将部分平行光束投射到被测带钢粗糙表面,按照物理学定律以一定的角度分布作散射,进入调制器的光与由带钢表面采集的散射光相互作用,使光的光学性质,如光的强度、相位、波长、频率、偏振态等,产生改变,成为被调制的信号光。再经过光纤送入光敏元件,由解调器解调后,获得带钢表面粗糙度初始参数,经滤波之后得到带钢表面粗糙度滤波输出参数。
冷轧带钢表面粗糙度在线检测设备安装于平整机组出口段,对经过平整处理之后的带钢表面粗糙度参数,包括表面轮廓算术平均偏差Ra、微观不平度十点高度Rz、峰值密度Pc等,进行实时检测。随着带钢按照一定的速度连续向前移动,可以实时地检测得到带钢表面粗糙度参数及其沿带钢长度方向的变化情况。
1.3 回归平滑自适应滤波算法设计
1.3.1 局部加权回归降噪预处理
将解调器输出的n组带钢表面粗糙度初始值定义为(xi,yi),i=1,2,…,n,其中:xi为采样点数,yi为带钢表面粗糙度初始参数(如表面轮廓算术平均偏差Ra、微观不平度十点高度Rz或峰值密度Pc)。对任意的第k组带钢表面粗糙度初始值(xk,yk),k=1,2,…,n,利用加权最小二乘法拟合如下d阶多项式:
(1)
式中:βj为估计系数,j=1,2,…,d。
为了得到拟和效果最佳的多项式,优化多项式的估计系数,将n组带钢表面粗糙度初始值与多项式计算结果之间的误差,进行加权求和并且最小化处理,得到如下方程:
(2)
式中:wk(xi)为一次权重函数,其表达式如下所示:
(3)
式中:hi为平滑窗口宽度。
1.3.2 二次平滑处理
(4)
式中:s为残差绝对值|ei|的中位数。
将降噪处理中得到的加权误差和Q改写为:
(5)

1.3.3 迭代寻优
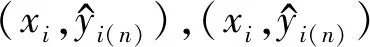
此外,在降噪预处理过程中,当带钢表面粗糙度初始值(xk,yk)与邻近数据(xk+1,yk+1)的变化yk+1-yk远超出设定阈值ε时,减小滤波算法平滑窗口宽度hi;如果带钢表面粗糙度初始值(xk,yk)与邻近数据(xk+1,yk+1)的变化yk+1-yk未超出设定阈值ε,则保持滤波算法平滑窗口宽度hi不变,其原理如下式所示:
(6)
式中:ε为预设可调阈值。
2 试验结果与分析
采用回归平滑自适应滤波方法对带钢表面粗糙度初始值进行滤波处理,操作流程如图2所示。在解调器中获得带钢表面粗糙度初始值之后先进行降噪预处理,输出带钢表面粗糙度初始值;定义一次权重为平滑窗口宽度的函数w,利用加权最小二乘法,拟合d阶多项式;估计系数βj并最小化加权残差平方和Q,降噪处理得到初始平滑值;之后基于平滑值与实际值的残差e,建立二次权重函数δ,将降噪处理中得到的加权误差加入函数并更新权重函数为δw,利用加权最小二乘法,多次迭代二次平滑处理步骤,在此期间如果粗糙度初始值中相邻数据点的差值超过阈值则减小平滑窗口的宽度,重复降噪预处理,最终计算得出,当取ε=0.75 μm时,可获得满意的平滑波形。
在解调器中获得的冷轧带钢表面轮廓算术平均偏差Ra初始参数的波形图如图3所示,分别应用回归平滑自适应滤波方法和高通滤波方法得到的带钢表面轮廓算术平均偏差Ra波形图如图4和图5所示。通过简单对比可以发现,未进行滤波处理的初始参数的波形图中存在低频成分,而应用回归平滑自适应滤波方法和高通滤波方法处理的波形图已经将低频成分剔除。将应用回归平滑自适应滤波方法得到的结果与标准方法测定的结果进行比较,结果显示两者之间的偏差为1.86%;应用高通滤波方法得到的结果与标准方法测定的结果进行比较,两者之间的偏差为5.89%。因此可推断回归平滑自适应滤波方法在冷轧带钢表面粗糙度信号提取上的精度高于高通滤波方法。
3 结论
(1) 自适应滤波方法利用前一时刻获得的带钢表面参数信息,自动调节现时刻的滤波参数,获得有用信号与噪声随机变化的统计特性,实现最优滤波,因此,更适合冷轧带钢粗糙度的实时在线测量。
(2) 回归平滑自适应滤波计算方法通过对表面粗糙度在线检测初始参数采用稳健局部加权回归进行降噪预处理,建立核函数,实现权值根据历史数据与当前数据的相对位置进行更新,当邻近数据变化超出设定阈值ε=0.75 μm时,自动减小平滑窗口宽度,实现粗糙度在线检测数据的自适应变步长回归平滑滤波。
(3) 应用回归平滑自适应滤波方法得到的结果与标准方法测定的结果之间的偏差为1.86%。应用高通滤波方法得到的结果与标准方法测定的结果进行比较,结果显示两者之间的偏差为5.89%。由此可知,回归平滑自适应滤波方法在冷轧带钢表面粗糙度信号提取上的精度高于高通滤波方法。

