钢-超高性能混凝土组合箱梁弹性弯曲性能试验研究及解析解

樊健生，王 哲，杨 松，陈 钒，丁 然

(1. 清华大学土木工程系，北京 100084；2. 清华大学土木工程安全与耐久教育部重点实验室，北京 100084；3. 清华大学水利水电工程系，北京 100084；4. 中电建路桥集团有限公司，北京 100048)

近几十年来，我国建成了众多的大跨径桥梁[1]，其中包括有港珠澳大桥等超级工程。然而，工程实践表明，对于常用的正交异性钢桥面系或钢-混凝土组合桥面系，桥面系病害或桥面系自重过大制约着桥梁跨径的提高[2]。

UHPC 作为一种力学性能优异的新型混凝土材料，近年来在结构工程尤其是桥梁工程中得到越来越多的应用[3 − 9]。将UHPC 作为桥面板，相比于正交异性钢桥面，其抗疲劳性能更优，能够降低疲劳病害；相比于普通混凝土桥面板，UHPC桥面板可做到更小的厚度，使得桥面系自重降低[10]。因此本文研究一种钢槽梁+UHPC 桥面板的新型组合桥面系，该桥面系有望应用于更大跨径的桥梁中。

对于钢-普通混凝土组合箱梁桥面系，国内外已有较多研究[11 − 19]。主要针对组合箱梁的整体抗弯承载力(加载点必须位于钢梁正上方)、界面滑移、剪力滞后效应、施工技术等。对于钢-普通混凝土组合梁的理论分析模型，Newmark 等[20]于1951年提出了考虑界面滑移效应的组合梁解析解；Nie等[21]深入研究了界面滑移效应对组合梁刚度的影响；孙飞飞等[22]推导了同时考虑剪切变形、滑移及剪力滞的工字钢组合梁的解析解，其模型中并未考虑钢梁的剪切翘曲；周旺保[23]推导了考虑上述效应的组合箱梁的解析解，但其模型中的钢腹板剪切变形仅与剪力荷载成正比，并未考虑腹板剪切变形的不均匀分布。

相比于钢-混凝土组合桥面系，已有的针对钢-UHPC 组合桥面系的研究偏少。田启贤等[24]针对正交异性钢箱梁+UHPC 板的组合桥面系开展了试验研究，包括钢-UHPC 组合梁和钢-UHPC 组合板的静力性能试验研究，以及组合桥面系的疲劳性能试验研究，结果表明该类型桥面系静力性能及疲劳性能良好。Yuan 等[25]同样针对该类型的桥面系的局部组合梁开展了疲劳性能试验研究，结果表明铺设UHPC 板显著降低了钢顶板的应力水平。邵旭东等[26 − 27]采用试验和数值模拟方法研究了钢-UHPC 组合板的整体抗弯及界面抗剪性能。刘诚等[28]研究了钢-UHPC 组合梁中栓钉连接件的疲劳性能。以上研究中主要研究对象为正交异性钢箱梁+UHPC 板的组合桥面系，其中的试验研究大多为梁、板等局部构件层面，桥梁节段尺度的试验较少；研究方法主要为试验研究和数值模拟，理论解析研究较少。

本文针对钢槽梁+UHPC 板的组合箱梁桥面系开展了大比例节段模型试验，关注组合桥面系整体抗弯性能，并针对弹性受力阶段的组合箱梁建立同时考虑剪力滞后、滑移效应以及钢腹板剪切变形的分析模型，并推导得出解析解，为新型桥面系的工程应用提供参考。

1 试验方案设计

1.1 试件设计

某实际工程桥梁桥面系方案中，钢腹板间距27 m、横隔板间距3 m、梁高3 m。在该桥面系方案的基础上，共设计了2 组钢-UHPC 组合箱梁构件，编号为CDS-1 和CDS-2，试件整体缩尺比例约为1∶3。然而缩尺后的桥面宽度尺寸仍较大，本试验重点研究桥面系纵向受力行为，考虑实验室场地及加载能力的限制，同时兼顾试验目标，最终减小腹板间距至3 m，使得四边约束的UHPC板仍满足单向板条件。

两个组合箱梁试件均采用UHPC 板+钢槽梁的截面形式，钢槽梁设计相同，变化参数为UHPC板厚度，如图1 所示。钢槽梁纵向总长度为3.2 m，横向宽度为3.16 m，高度为1 m，腹板采用8 mm厚钢板，其余钢板均为6 mm 厚。箱梁腹板中心间距为3 m，设有水平及竖直加劲肋；横隔板间距为1 m，同样设置了双向加劲肋。相邻横隔板之间的底板中间区域作开洞处理，目的是方便观测UHPC 板底的开裂行为。

UHPC 板纵向长3.2 m，横向宽4 m，厚度分别为60 mm(CDS-1)和90 mm(CDS-2)。UHPC 板与钢槽梁的连接采用栓钉连接件，栓钉直径13 mm、高35 mm，焊接在腹板上翼缘(布置3 列)及横隔板上翼缘(布置1 列)。UHPC 板中配置双层钢筋网，纵横钢筋均为 8@100，采用HRB400 级螺纹钢筋，两层钢筋网横筋在内、纵筋在外，保护层厚度为8 mm。

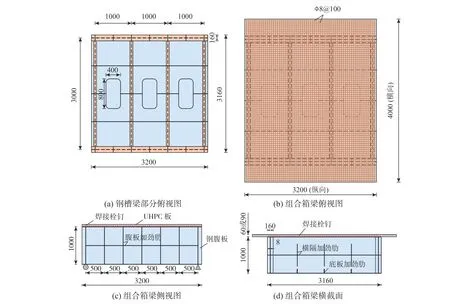
图1 试件设计 /mm Fig. 1 Test specimen design

两个组合箱梁试件的主要设计参数汇总如表1所示。

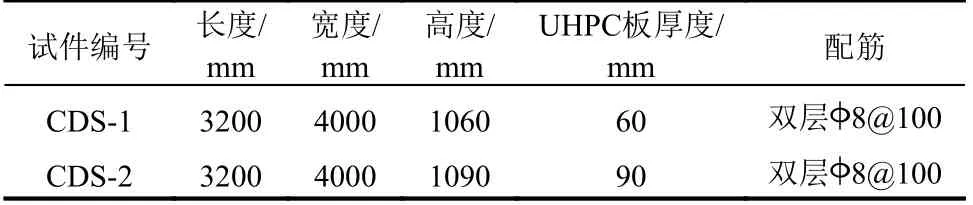
表1 试件主要参数Table 1 Parameters of specimens

1.2 材料性能

本文中采用的UHPC 配合比如表2 所示。钢纤维选用长13 mm、直径为0.2 mm 的平直型钢纤维，其体积掺量为2.5%。UHPC 采用高温蒸汽养护，具体步骤为：浇筑结束后覆膜养护48 h，然后放入养护室中90 ℃高温蒸养48 h。UHPC 抗压强度采用边长100 mm 的立方体试块测得，并按照折减系数0.9 换算为轴心抗压强度[29]；UHPC 轴心抗拉强度采用狗骨试件[30]测得。

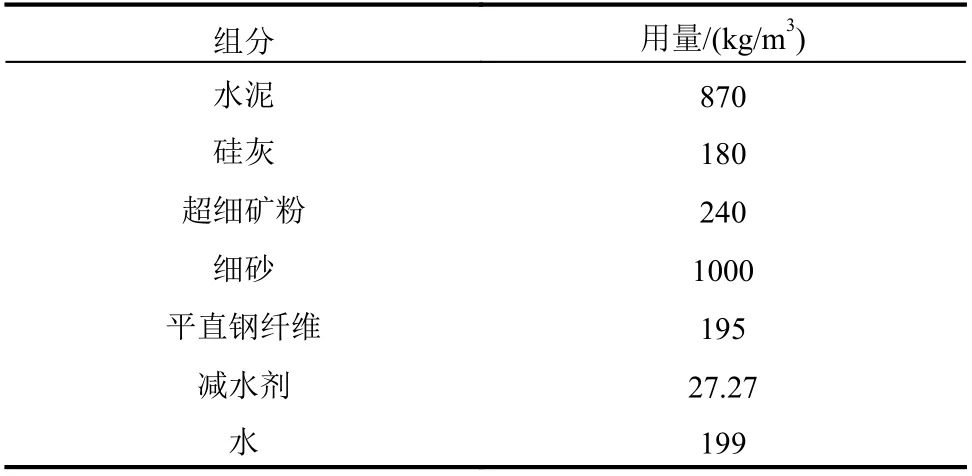
表2 UHPC 配合比Table 2 Mix proportions of UHPC

材性试验测得的UHPC、钢筋及钢板的主要力学性能见表3。

1.3 试验装置及加载方案

试验重点关注组合箱梁试件的纵向受力性能，考虑到实验室加载条件，设计纵向对边简支边界条件，在两端横隔板正下方设置支座。

CDS-1 和CDS-2 加载装置如图2 所示。加载位置位于两侧腹板跨中正上方，加载点位置垫有100 mm×100 mm 钢垫板，最大荷载基于精细有限元模型结果确定，不超过有限元模型中钢板屈服时荷载的85%，且试验中持续观测试件各处应变达到全程控制。

为了保证两处加载点的荷载一致，两个千斤顶共用同一液压油路。

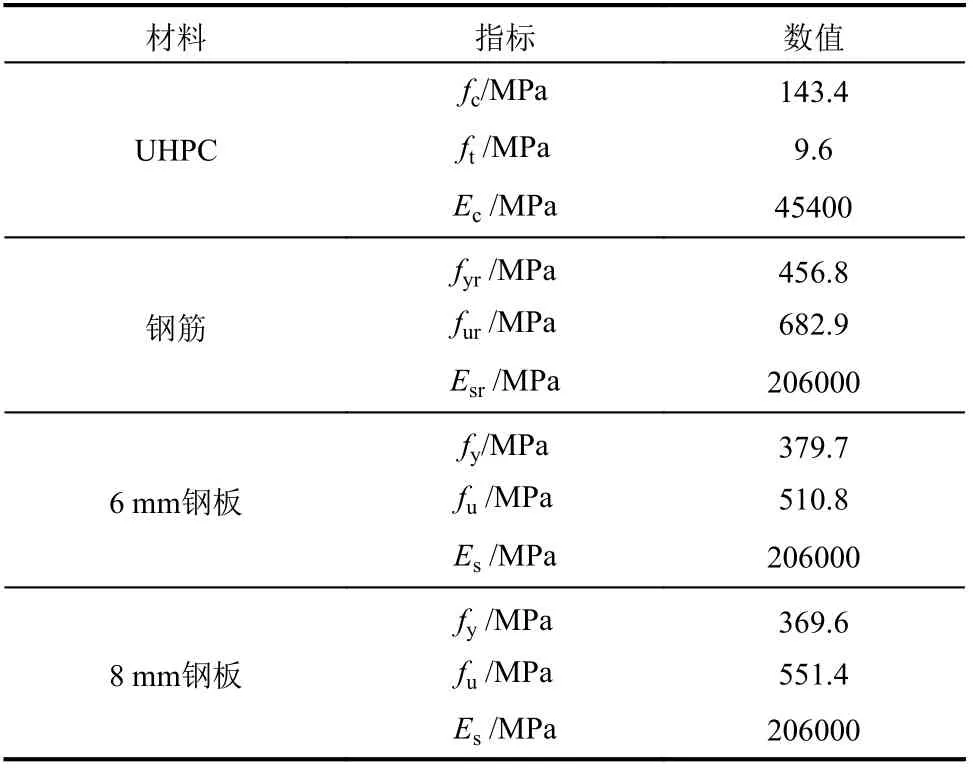
表3 材料力学性能Table 3 Material properties

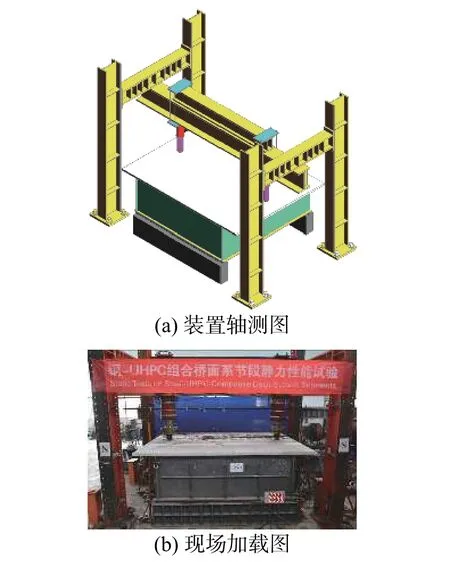
图2 加载示意图Fig. 2 Test setup

1.4 测点布置及量测方案

测点布置如图3 所示。两个试件的测点布置一致。

2 试验结果及分析

2.1 荷载-挠度曲线

为了保证试件处于弹性阶段并且得到可靠的试验数据，试验加载至1000 kN(两个千斤顶各500 kN)停止。试验测得的总荷载-UHPC 板跨中挠度曲线及总荷载-钢梁跨中挠度曲线如图4 所示。由图可知，荷载-挠度曲线基本均为直线，试件刚度未降低，这表明材料整体处于弹性范围内。由于加载点位于钢梁腹板正上方，横向UHPC 板中点的挠度略低于钢梁腹板处挠度。

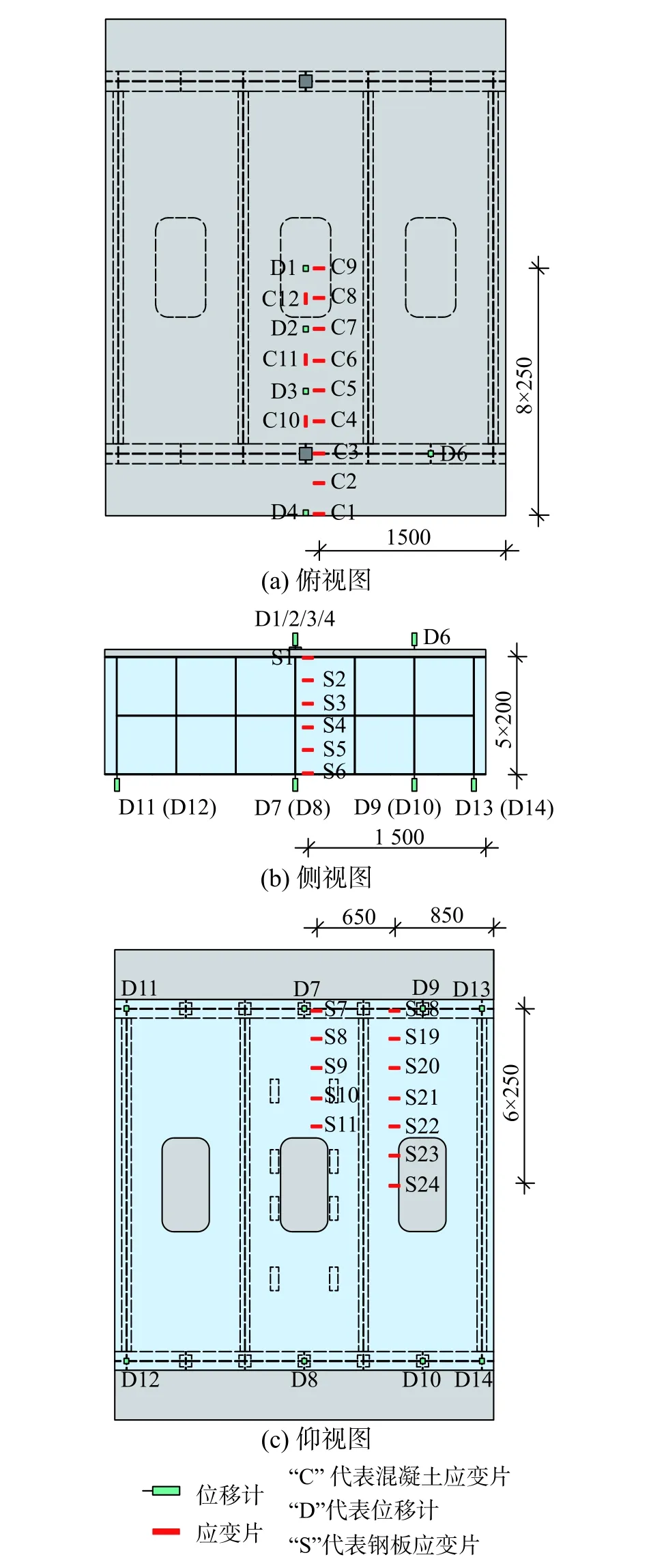
图3 测点布置图 /mm Fig. 3 Arrangement of measurement devices

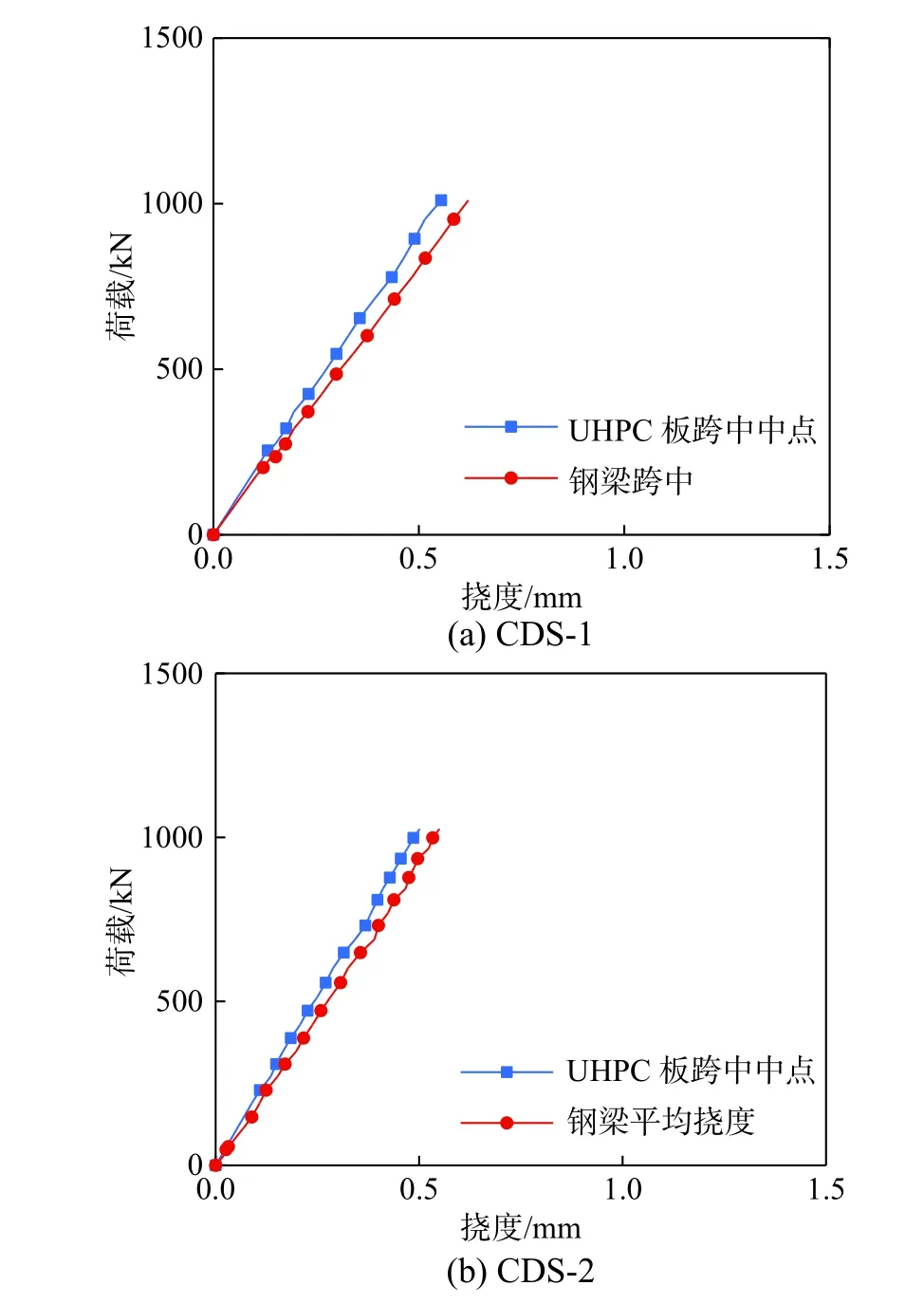
图4 荷载-挠度曲线Fig. 4 Load-deflection curves

试件的挠度结果列于表4，可知CDS-2 的UHPC板跨中挠度及钢梁跨中挠度均低于CDS-1。

表4 试件挠度Table 4 Deflection of specimens

2.2 跨中挠度分布

试验中测量了跨中截面多个测点的挠度，挠度沿横向分布的形式如图5 所示。可见加载点挠度略高于其余测点，并且距离加载点越远，挠度相对越小，但是不同测点间的差值较小，后文进行简化分析时可忽略该差异。

2.3 跨中应变分布曲线

试件主要在跨中附近截面布置了应变片，对于UHPC 板及钢梁底板的纵向应变，其横向分布如图6 所示。由于存在剪力滞后效应，钢腹板附近的应变较大，应变随着距钢腹板距离的增大而减小，截面最大压应变与最小压应变之比约为5～7。由图可知，跨中截面CDS-2 的UHPC 板顶压应变明显低于CDS-1，而钢底板应变较为接近，规律并不明显，有待理论解析解的进一步对比。

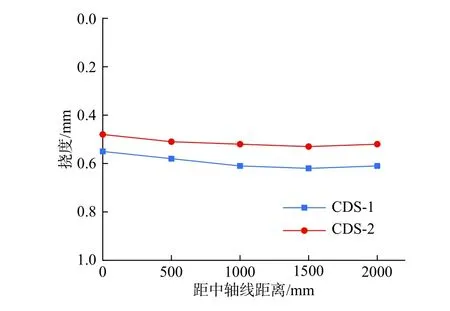
图5 跨中挠度横向分布Fig. 5 Transverse distributions of midspan deflections

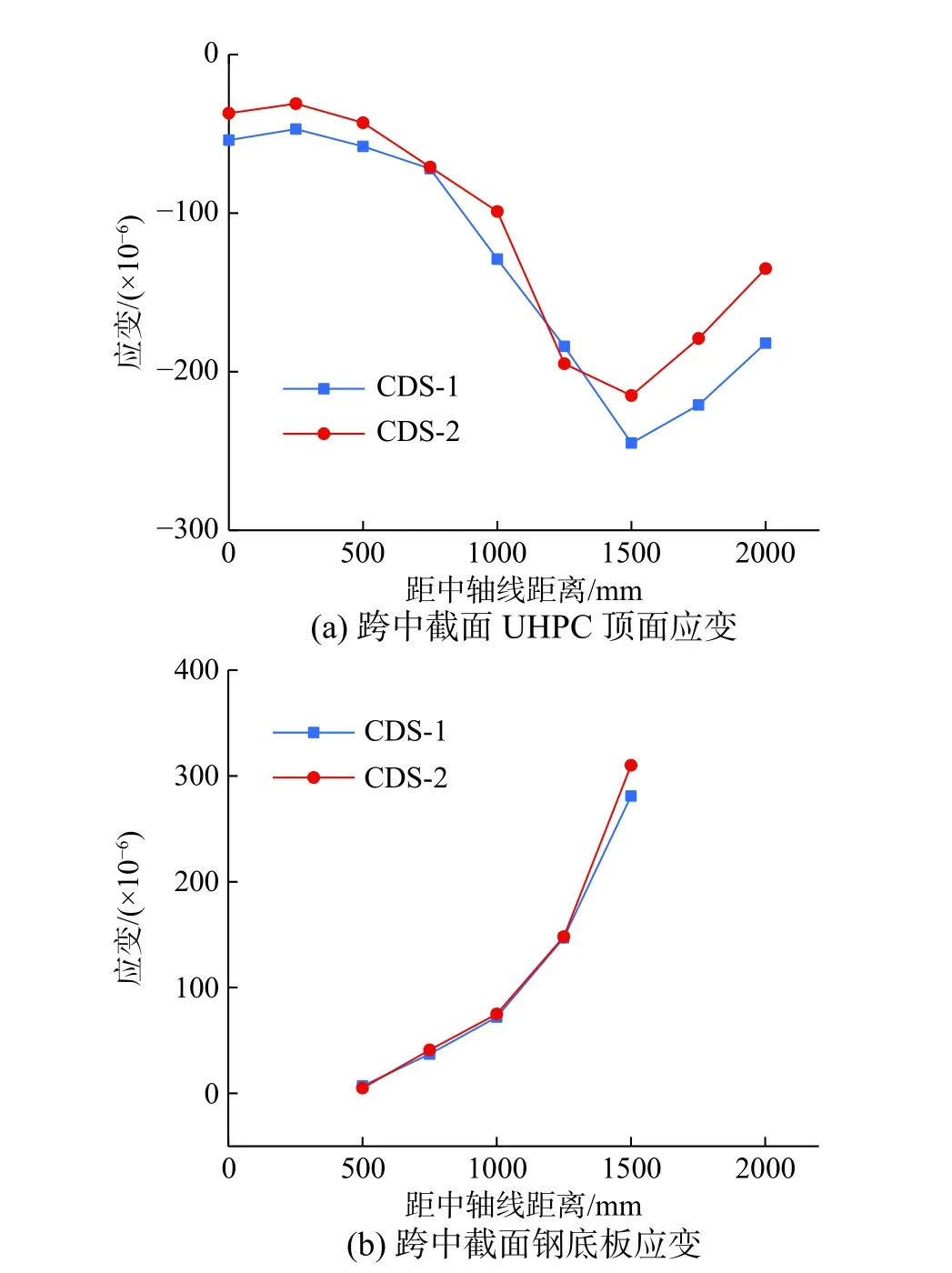
图6 纵向应变的横向分布Fig. 6 Transverse distributions of longitudinal strains

3 组合箱梁解析解

基于本文试验，建立考虑剪力滞后、界面滑移效应以及钢腹板剪切变形的组合箱梁分析模型。

3.1 基本假定

本文后续分析的开展基于以下假定：

1)由于混凝土板的厚度相对于其他方向的尺寸一般较小，因此对于混凝土板忽略其面外剪切变形；

2)钢梁上翼缘尺寸相对较小，将其与钢腹板统一考虑；

3)分析结构在弹性阶段的变形，混凝土、钢材、界面连接件的本构均为线弹性、位移可简单叠加；

4)忽略混凝土板与钢梁之间的竖向分离；

5)混凝土板的变形与钢梁的变形分别满足平截面；

6)忽略钢腹板剪切变形对于界面滑移的影响。

3.2 分析模型

针对如图7 所示的常见的钢槽梁+混凝土板的组合箱梁截面进行分析，图中b1、b2、b3、b4、tc、t1、t2、t3、hw分别表示钢腹板间混凝土板宽度的一半、悬臂混凝土板的宽度、钢腹板间钢底板宽度的一半、钢梁上翼缘宽度、混凝土板厚度、钢梁上翼缘厚度、钢腹板厚度、钢底板厚度和钢腹板高度。

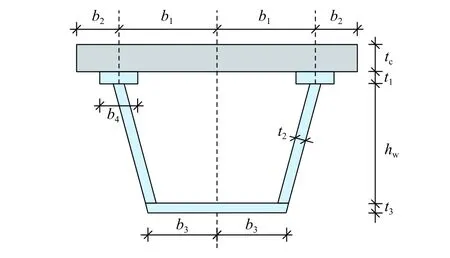
图7 典型组合箱梁截面Fig. 7 Typical section of composite box girder

取组合箱梁中的微单元，分析其变形特征，单元变形前后如图8 所示。图中oc、ocs、os、osb分别表示混凝土板形心轴位置、组合换算截面中和轴位置、钢梁形心轴位置、钢底板形心轴位置，hc、hs分别表示混凝土形心轴和钢梁形心轴距组合换算截面中和轴的距离，hb、hsu分别表示钢梁形心轴距钢底板形心轴和组合梁界面的距离。建立如图8 所示的直角坐标系，x轴平行于组合梁长度方向，以支座位置为零点，且经过ocs；z轴垂直于混凝土板平面，且正方向为oc指向os；y轴以钢梁对称轴平面的位置为零点。

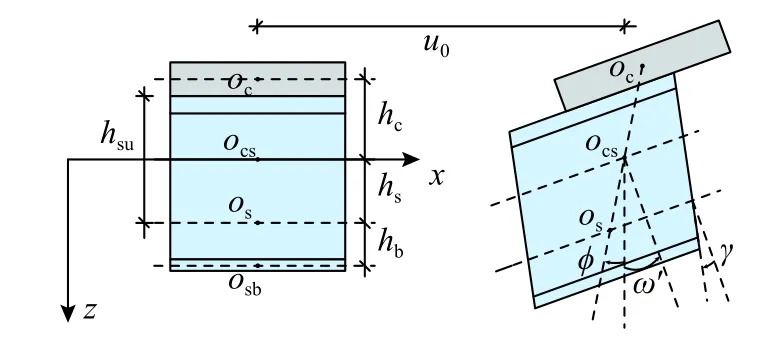
图8 分析模型Fig. 8 Analytical model

在竖向荷载作用下，组合箱梁发生变形，组合箱梁任意一点的位移主要由界面滑移导致的位移、组合箱梁挠曲导致的位移和剪切变形(包括翼板剪力滞后以及钢腹板剪切)导致的位移三部分组成。假设ocos在xz平面内的转角为 ϕ(顺时针为正)，组合梁竖向挠度为ω(与z轴反向)，钢梁在xz平面内的剪切应变为γ(顺时针为正)，xy平面内的剪力滞翘曲位移(与x轴同向)强度函数为f(x)、翘曲位移形函数为ψ(y)。则混凝土板任意一点的纵向位移可表示为：

根据Sun 等[31]的研究，剪切翘曲形函数采用二次函数形式已经相当精确，因此本文选取以下形式的形函数：

式中：α1、α2、α3为翘曲形函数相对幅值；D为考虑轴力自平衡的轴向均匀位移，为确定上述未知参数，参考文献[32]中的方法，由最小势能原理，求得：

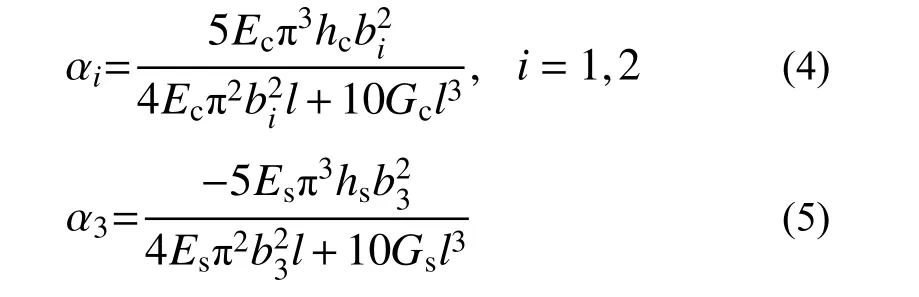
式中，Ec、Gc、Es、Gs、l分别为混凝土弹性模量、混凝土剪切模量、钢板弹性模量、钢板剪切模量、组合箱梁跨度。

由轴力自平衡，得到：

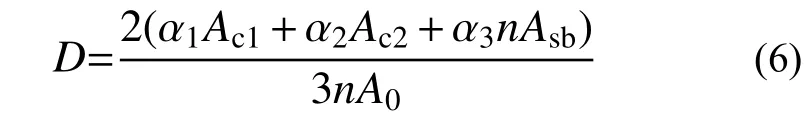
式 中，n=Es/Ec，Ac1=2b1tc，Ac2=2b2tc，Asb=2b3t3，A0为换算截面面积之和。

3.3 势能表达式

忽略板件的面外剪应变，求得箱梁各点的应变为(为缩短篇幅，后文中所有导数符号均表示对x求导，所有以x为自变量的函数均写成简化形式，例如f′表示df(x)/dx)：

根据虚功原理，组合箱梁的总势能表达式为：

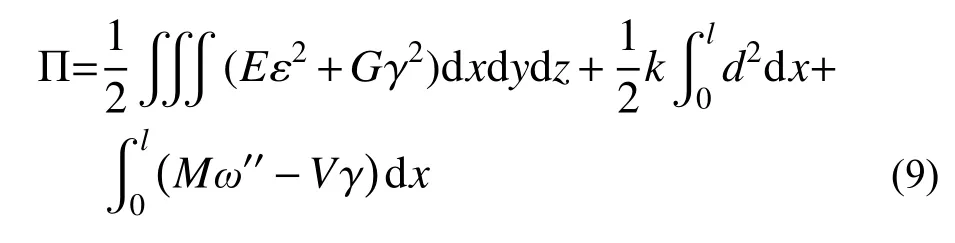
式中，k为单位长度的界面剪切刚度。

将式(7)和式(8)代入式(9)，得到：

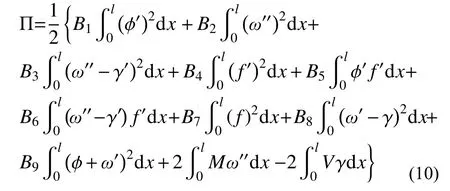
式中，B1～B9由截面特性决定，由于表达式篇幅较长，此处不展开。

3.4 平衡微分方程及求解

根据最小势能原理，在一切“可取位移”中，弹性体的真实位移应使其总能量取最小值，则对总势能求变分，有：

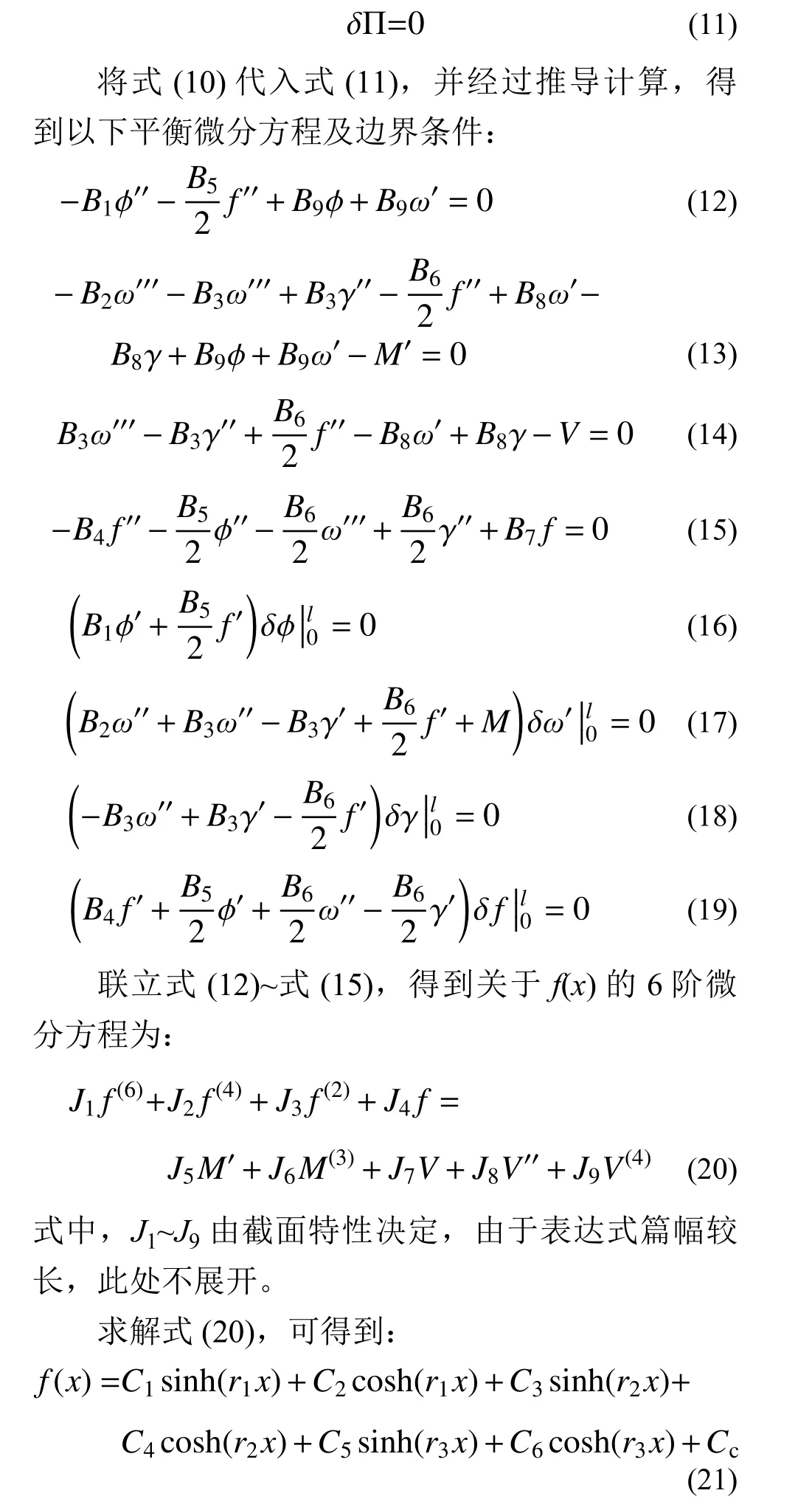
式中：C1～C6为待定系数，需要由位移、变形等边界条件确定；Cc是仅与截面形式和荷载条件有关的系数；r1～r3仅与J1～J4相关；上述求解过程较为简单，此处不赘述。

将式(21)代入式(12)～式(15)，可得：

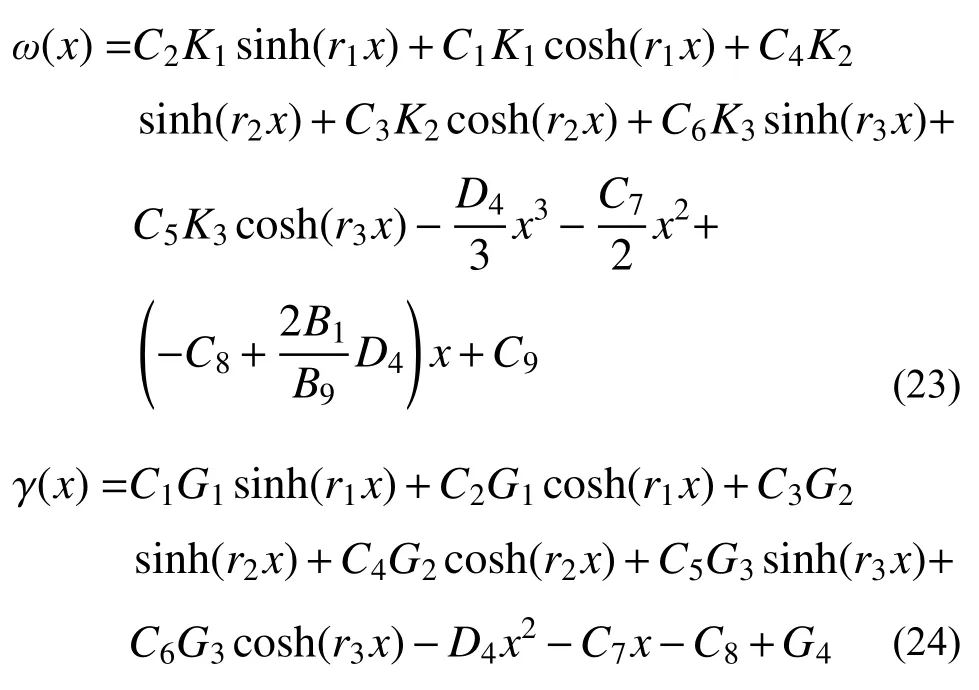
式中：D1～D4、K1～K3、G1～G4是仅与截面形式和荷载条件有关的系数；C7～C9为待定系数，需要由位移、变形等边界条件确定。

3.5 解析解的验证

基于本文试验，考虑组合箱梁的变形，由于试件及边界均具有对称性，因此只需考虑0≤x≤l/2 的半跨箱梁。外力V(x)=P/2。

对于跨中单点加载的简支梁，显然可得以下边界条件：

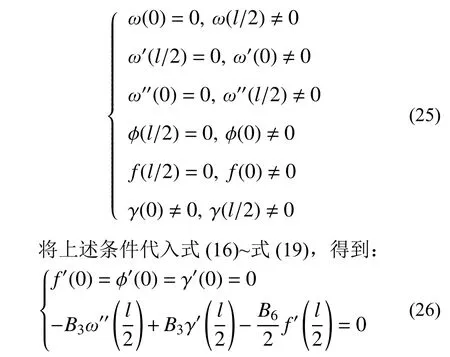
将式(21)～式(24)代入式(25)和式(26)的边界条件，可求得系数C1～C9的值。

计算总荷载P=1000 kN 时的试件变形，并验证文献[11]中不考虑腹板剪切变形的方法。如图9所示为跨中截面纵向应变沿横向的分布情况，本文解析解与试验值基本吻合，而不考虑腹板剪切的解析解明显低估了纵向应变大小，主要原因是本文试件的跨高比相对较小，腹板剪切变形不可忽略。但试验值未能完全落在解析解的曲线上，原因主要包括：1)解析解存在较多的假定，实际构件中受力情况复杂，理论推导无法完全准确地描述构件的行为；2)试验的应变测量本身具有一定误差，该误差包括不可避免的系统误差以及难以预测的偶然误差；3)为了满足观测需求，实际构件在钢底板做开洞处理，增加了构件受力的复杂性。

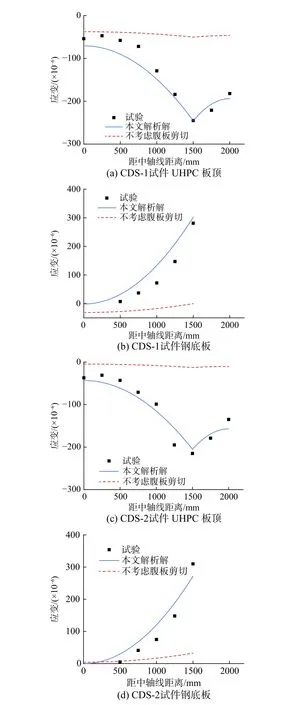
图9 跨中纵向应变分布的解析解与试验值对比Fig. 9 Comparison between analytical and experimental longitudinal strain distributions in midspan

图10 所示为P=1000 kN 时组合箱梁挠度沿纵向的分布情况，可见不考虑腹板剪切的解析解预测效果较差。对于试件CDS-1，实际跨中挠度为0.55 mm，本文解析解挠度为0.50 mm，误差约为9.1%；对于试件CDS-2，实际跨中挠度为0.48 mm，本文解析解挠度为0.42 mm，误差约为12.5%。实际试件中钢底板共有3 处开洞处理，解析解无法考虑该实际情况，因而挠度的计算存在一定低估。

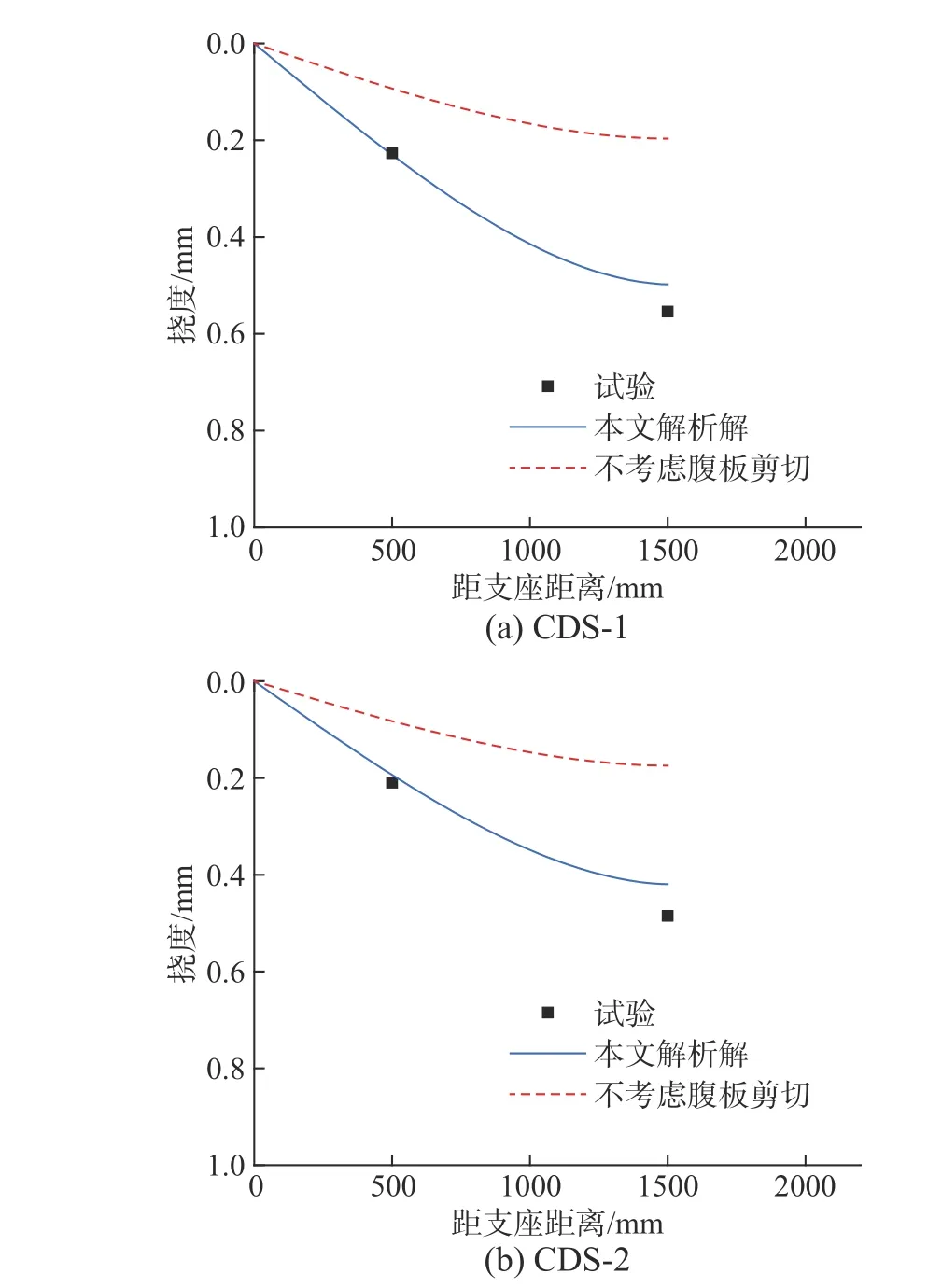
图10 箱梁挠度的解析解与试验值对比Fig. 10 Comparison between analytical and experimental deflections of box girder

汇总理论模型结果如表5 所示，可知相同荷载下，UHPC 板厚越大，组合梁跨中挠度越小、UHPC 板和钢底板应变水平越低。

表5 理论模型主要结果Table 5 Main results of theoretical model

4 结论

本文通过大比例试验，针对新型钢-UHPC 组合箱型桥面系开展了研究，并推导考虑剪力滞后、滑移效应以及钢腹板剪切变形的组合箱梁解析解，得出以下主要结论：

(1) 集中荷载作用下，剪力滞效应较为明显，UHPC 跨中截面纵向压应变的最大值与最小值之比约为5～7；

(2) 相同荷载下，随着UHPC 板厚增加，钢-UHPC 组合箱梁的刚度提高，UHPC 板和钢梁应变和应力水平均降低；

(3) 加载点位于钢腹板正上方的工况下，组合箱梁挠度的横向差异较小；

(4) 跨高比较小的情况下，钢腹板剪切变形不可忽略，与仅考虑剪力滞后和滑移效应的模型相比，考虑剪力滞后、滑移效应以及钢腹板剪切变形的组合箱梁解析解与试验值吻合更好，误差相对较小。