基于MapReduce和Spark的大规模压缩模糊K-近邻算法

王谟瀚,翟俊海,b,齐家兴

(河北大学 a.数学与信息科学学院; b.河北省机器学习与计算智能重点实验室,河北 保定 071002)

0 概述

K-近邻(K-Nearest Neighbor,K-NN)[1]是一种常用的分类方法,广泛应用于模式识别、数据挖掘和机器学习等领域。K-NN方法简单且易于编程实现,但是其存在2个问题,一是对测试样例进行分类时需要存储训练集中的所有样例,并计算测试样例与训练集中所有样例之间的距离,二是对于每一个测试样例,用训练集中的样例对它们进行分类时,每个训练样例被认为是同等重要的。

针对第一个问题,HART[2]于1968年提出了压缩近邻(Condensed Nearest Neighbor,CNN)算法。但是,CNN算法对噪声非常敏感,且其结果与样例选择顺序有关。对此,研究人员提出了较多改进算法,如RNN(Reduced Nearest Neighbor)[3]、ENN(Edited Nearest Neighbor)[4]和ICF(Iterative Case Filtering)[5]等。近年来,针对K-NN对测试样例进行分类时需存储训练集中所有样例的问题,学者们也提出了一些较好的解决方法。HOU等人[6]将哈希技术与决策树相结合,提出基于树的紧哈希方法,该方法可显著提高近邻样例的搜索效率。梁聪等人[7]提出一种基于参考点的改进K-NN分类算法。该算法依据点到样本距离的方差选择参考点,并赋予参考点自适应权重,与基本K-NN算法及kd-tree近邻算法相比,其具有较高的分类精度及较低的时间复杂度。基于谱哈希技术,WAN等人[8]提出针对高维数据的近似近邻搜索算法。基于分布式哈希技术,文庆福等人[9]提出一种近似近邻搜索方法。ALVAR等人[10]使用局部敏感哈希技术,提出针对大规模数据集的样例选择算法,该算法的时间复杂度达到线性级。针对投影哈希中投影误差较大、二进制编码时原始信息丢失严重等问题,杨定中等人[11]提出一种近似最近邻搜索方法,该方法通过多阶段量化策略降低编码过程中的投影及量化误差。罗辛等人[12]提出一种基于相似度支持度的最近邻度量方法,其在保证分类精度的前提下降低了计算复杂度。乔玉龙等人[13]利用向量的方差和小波域中的逼近系数得出2个重要不等式,利用不等式排除不可能成为K-近邻的向量,进而降低了计算复杂度。受交叉验证思想的启发,ZHAI等人[14]提出交叉样例选择算法,该算法可解决大规模样例的选择问题。SONG等人[15]将针对分类问题的样例选择算法移植到回归场景,提出一种针对K-NN回归问题的排序样例选择算法,其扩大了样例选择的应用范围。

近年来,大数据技术在很多领域得到广泛关注与应用,一些科研人员针对大数据的近邻搜索问题进行了研究。基于开源大数据平台,MUJA等人[16]提出具有可扩展性的最近邻算法。基于MapReduce大数据计算平台,ZHAI等人[17]设计基于投票机制和随机权网络的大数据样例选择算法。基于Spark大数据计算平台,MAILLO等人[18]提出大数据K-近邻搜索算法。SONG等人[19]对基于MapReduce的K-NN算法进行了具体的理论分析。

针对第二个问题,KELLER[20]于1985年提出了模糊K-NN算法。然而,模糊K-NN算法依然存在上述第一个问题。为此,ZHAI等人[21]提出了压缩模糊K-近邻(Condensed Fuzzy K-NN,CFKNN)算法。但是,CFKNN算法仅适用于中小数据场景,在大数据环境中,CFKNN会出现计算效率低的问题,甚至不可实现。此外,CFKNN的样例选择采用静态机制,导致该算法的性能提升存在局限性。

为了解决上述问题,本文基于MapReduce和Spark提出2种大规模压缩模糊K-近邻算法。将CFKNN算法扩展到大数据环境,在MapReduce和Spark 2种并行计算框架上实现面向大规模数据环境的压缩模糊K-近邻算法,以降低CFKNN的计算复杂度并缩短算法的运行时间。在样例选择过程中,对阈值进行动态调整,从而提高算法的动态特性。

1 相关知识

1.1 CFKNN算法

设T是训练集,S是所选样例的集合,C为训练集的类别属性,训练集共分为p类。在初始时,从训练集T中的每类随机选择一个样例加入S,然后根据算法1计算S中样例的模糊隶属度,用算法2确定x的类别隶属度,并通过类别隶属度计算样例x的信息熵。如果样例x的信息熵大于所设阈值 ,则将样例x加入到S中,否则丢弃x。当训练集T为空时,算法终止,输出所选样例集合S。CFKNN算法的伪代码如算法3所示。

算法1模糊隶属度算法

输入所选样例集合S

输出样例的隶属度μij=μj(xi),1≤i≤n,1≤j≤p

1.对于∀j,1≤j≤C,计算每一类的中心Cj

2.对于∀i,j,计算xi到各类中心Cj的距离dij

3.对于∀i,j,按式(1)计算μij=μj(xi),1≤i≤n,1≤j≤p

4.返回样例隶属度

(1)

算法2F-KNN算法

输入所选样例集合S{(xi,yi)|xi∈Rd;yi∈Y},1≤i≤n,样例x

输出样例x隶属于每一类的隶属度μj(x),1≤j≤p

1.利用算法1计算S中每一个样例的类别隶属度μij=μj(xi),构成一个n行p列的矩阵μ

2.在S中找到x的K个近邻

3.利用式(2)确定x的类别隶属度:

(2)

4.输出j(x)

算法3CFKNN算法

输入训练集T,参数k和α(假设T的样本容量为n,T中的样例共分为p类)

输出S⊆T

1.从T中的每类随机选一个样例加入S中

2.For x in T-S do

3.根据算法1计算S中样例的类别隶属度

4.用算法2确定x的类别隶属度(μ(x,C1),μ(x,C2),…,μ(x,CP))

5.根据式(3)计算x的熵Entr(x):

(3)

6.If Entr(x)>α

7.S=S∪{x}

8.End if

9.End for

10.Return S

1.2 MapReduce和Spark并行计算框架

MapReduce[22]是由Google公司提出的一种面向大规模数据的并行计算模型,MapReduce继承了函数式编程语言LISP中map函数和reduce函数的思想,采用分治策略处理大数据。在初始阶段,MapReduce自动将大数据集划分为若干子集部署到云计算节点上,map阶段将数据变换为键值对数据。reduce阶段在map阶段的基础上,对已经归纳好的数据做进一步处理,得到最终计算结果。通过map和reduce 2个阶段,完成对大规模数据的并行化处理。

Spark[23]是处理大数据的快速通用引擎,2009年由加州大学伯克利分校对外开源,随后凭借其快速、通用以及可扩展等优势,迅速成为Apache顶级项目。Spark起初是为了克服Hadoop并行计算框架的不足而被提出,发展至今,Spark已经成为包含SparkSQL、Spark Streaming、Spark GraphX和Spark MLlib等子项目在内的生态系统。Spark将MapReduce基于磁盘的存储和容错机制改为基于内存的机制,提高了计算速度。通过将执行模型抽象为有向无环图(Directed Acyclic Graph,DAG),并根据弹性分布式数据集(Resident Distributed Dataset,RDD)间的宽依赖和窄依赖关系,串联或并行执行多个阶段的任务,无需将不必要的中间结果输出到HDFS(Hadoop Distributed File System)上,以此提高计算效率。

RDD和算子是Spark的核心与基础。RDD是Spark中的基本数据抽象,其为不可变、可分区、可并行计算的数据集合。在具体的逻辑实现上,RDD将数据分为若干分区,分区以分布式方式保存在云节点上,既可以存储在内存中,也可以存储在外存中。当某些数据需要重复使用时,RDD允许用户显式地将数据缓存在内存中,从而有效提高了计算速度。在对RDD中的数据进行处理时,需要通过Spark算子来实现相应的数据操作。一般根据是否会触发Spark作业执行将Spark算子分为如下两类:

1)转换算子,其对RDD进行转换操作,将一个RDD转换为另一个RDD。转换算子的转换操作是延时加载的,它们不会直接返回计算结果,只记录转化动作。

2)行动算子,其触发Spark作业执行,得到Spark作业的计算结果。

2 大规模压缩模糊K-近邻算法

2.1 算法描述

通过对原始CFKNN算法进行分析可以得出,该算法难以在大数据环境下进行应用的3个主要原因具体如下:

1)在确定T中样例x的类别隶属度时,首先需要计算集合S的隶属度矩阵m,然后寻找k个近邻,计算样例x的类别隶属度。当训练集T为大数据集时,集合S中样例增多,对T中的每个样例寻找S中的k个近邻并计算T中每个样例的熵值时,算法计算量很大,算法运行时间超出可接受范围。

2)当训练集为大数据集时,寻找k个近邻的计算复杂度大幅增加。

3)对所选样例集合S不能实时更新,进而导致对当前样例x的隶属度和信息熵计算不准确,这是导致原始CFKNN算法无法在大数据环境下应用的主要原因。

针对以上问题,本文提出大规模压缩模糊K-近邻算法,该算法对原始CFKNN做出如下改进:

1)针对第一个问题,大规模压缩模糊K-近邻算法在计算样例x的类别隶属度时,先在S中寻找样例x的k个近邻,然后只计算k个样例的类别隶属度,从而大幅降低了由于计算S中所有样例的隶属度所引起的计算复杂度(对应算法4第5行)。

2)利用并行计算框架,在每个计算节点上并行地寻找集合S中样例x的k个近邻,从而解决第二个问题。

3)对于第三个问题,本文在阈值设置上引入动态机制,对阈值进行动态调整,将阈值α设置为迭代次数j的单调递减函数,如式(4)所示。其中,设置初始阈值initEntropy时考虑到对应类别数的最大熵(对应算法4第6行)。通过引入动态阈值机制,使得本文算法训练出的分类器较原始CFKNN算法具有更好的分类精度。

(4)

其中,j为当前迭代次数,n为总迭代次数。

本文基于并行计算框架的大规模压缩模糊K-近邻算法伪代码如算法4所示,算法流程如图1所示。

算法4大规模压缩模糊K-近邻算法

输入数据集T,近邻数k,阈值α,迭代次数iterations

输出数据子集S⊆T

1.for iteration in iterations do

2.初始化S,T

3.根据式(3)并行计算T中每个样例x的信息熵Entr(x)

4.根据式(4)计算α(j,n)

5.if Entropy>α(j,n)

6.S=S∪{x}

7.End if

8.输出S

9.End for

图1 大规模压缩模糊K-近邻算法流程

2.2 基于MapReduce的压缩模糊K-近邻算法

在原始CFKNN算法中,当T为大数据集时,针对T中的每个样例,在S中寻找其k个近邻以及计算T中每个样例熵值的过程,会大幅提高算法的计算量。因此,本文将此过程通过MapReduce框架进行并行执行。对于T中的样例,并行寻找S中k个近邻并计算熵值,从而大幅缩短算法的运行时间。随着T中样例数量的增加,可以通过增加计算节点个数,使得算法维持可接受的运算时间并容易扩展。大规模压缩模糊K-近邻算法在MapReduce中的计算,即基于MapReduce的压缩模糊K-近邻(MR-CFKNN)算法流程如算法5所示。该算法分为Mapper阶段和Reducer阶段2个部分,Mapper阶段包含setup和map 2个方法,Reducer阶段只包含reduce方法。在Mapper阶段的setup方法中,首先对数据子集S进行初始化(算法5第3行),map方法计算输入的样例t∈T在S中的k个近邻(算法5第6行),由k个近邻计算出t的熵值Entropy(算法5第7行),若Entropy大于熵的阈值α,则输出样例t。Reducer阶段不做任何操作直接输出所选样例。

算法5MR-CFKNN算法

输入数据集T,近邻数k,阈值α

输出数据子集S⊆T

1.ClassMapper

2.执行setup()方法,对所需资源进行初始化

3.初始化数据子集S⊂T

4.初始化参数k,initEntropy

5.使用map方法对样例进行格式化操作,map(sid id,instance t)

6.使用findKNN方法找到当前样例的k个近邻,Array kNearestNeighbor=findKNN(t,S,k)

7.使用fKNN方法计算当前样例的熵,Entropy=fKNN(kNearestNeighbor,t)

8.If Entropy>α

9.context.write(NullWritable,t)

10.End if

11.Mapper end

12.Class Reducer

13.使用reduce方法对样例进行格式化,reduce(NullWritable,[t(1),t(2),…])

14.for t in[t(1),t(2),…] do

15.输出所选样例,context.write(NullWritable,t)

16.End for

17.Reducer end

2.3 基于Spark的压缩模糊K-近邻算法

算法6Spark-CFKNN算法

输入数据集T,近邻数k,阈值α,迭代次数iterations

输出数据子集S⊆T

1.对数据集T进行初始化RDD操作,valtrainInitRDD = sc.textFile(T)

2.得到初始样例集合D,var dRDD = trainInitRDD.combineByKey().map().flatmap()

3.得到T与D的差集,var tRDD = trainInitRDD.subtract(dRDD)

4.for(i<-0 until iterations)do

5.对数据集D进行广播操作,var dInsbroad = sc.broadcast(dRDD.collect())

6.valdistanceRDD=tRDD.map(line => {

7.for(i<-0 until dInsbroad.value.length) do

8.计算当前样例与D中样例的距离,Distance(dInsbroad.value(i),line)

9.End for

10.})

11.valtEntropyAndSelectRDD= distanceRDD.map(line=>{

12.计算当前样例的隶属度,memShipDevide(trainInsMemberShipCalc(kNearestNeighbor))

13.计算当前样例的熵值,val Entropy=calcEntropy()

14.If Entropy>α

15.Sm=Sm∪{x}

16.Tm=Tm-{x}

17.End if

18.})

19.将当前迭代所选样例与D求并集,dRDD = dRDD.union(tEntropyAndSelectRDD)

20.将T与当前迭代所选样例做差集,tRDD = tRDD.subtract(tEntropyAndSelectRDD)

21.End for

3 实验结果与分析

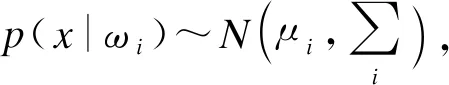
p(x|ω1)～N(0,I)

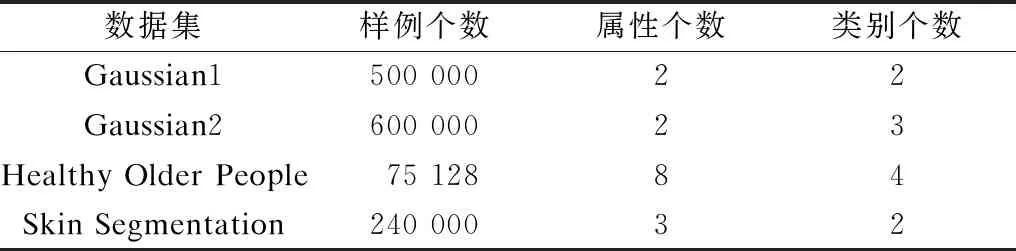
表1 数据集基本信息

表2 高斯分布参数

本文从文件数目、同步次数、分类精度、所选样例个数以及算法运行时间等方面,将MR-CFKNN算法和Spark-CFKNN算法进行对比。此外,分别将原始CFKNN算法和本文算法所筛选出的样例作为训练集,使用KNN算法对测试集进行分类并比较分类精度。在实验过程中,分别从4个大数据集中随机选取部分样例作为测试集,测试集基本信息如表3所示。实验所用的大数据平台环境的配置信息如表4所示, 大数据平台环境的节点规划如表5所示。

表3 测试集基本信息

表4 实验配置信息

表5 大数据平台环境的节点规划

表6所示为原始CFKNN算法与本文大规模压缩模糊K-近邻算法在Guassian1数据集上的实验结果。从表6可以看出,CFKNN算法只对所有训练样例进行1次迭代,MR-CFKNN算法和Spark-CFKNN算法分别进行了3次、4次和5次迭代。表中所示的分类精度是分别将原始CFKNN算法、本文算法所筛选出的样例集合作为训练集,使用KNN算法进行分类精度测试的结果。大规模压缩模糊K-近邻算法的分类精度优于原始CFKNN算法的主要原因有2点:首先,CFKNN算法只对训练集进行1次迭代,为了保证所选样例更具代表性,同时考虑到阈值为固定值,所以CFKNN算法需要将阈值设置为中间数值,这会导致在算法运行初期选入较多的非边界样例;其次,大规模压缩模糊K-近邻算法考虑算法运行初期训练样例的熵值普遍较高的情况,且随着算法的不断迭代,训练样例的熵值逐渐接近真实值,所以其引入了动态阈值策略,使阈值随着迭代次数的增加而逐渐衰减,以此来克服原始CFKNN算法的缺点。以上2点使得大规模压缩模糊K-近邻算法的分类精度优于原始CFKNN算法,说明本文算法所筛选出的样例更具代表性。

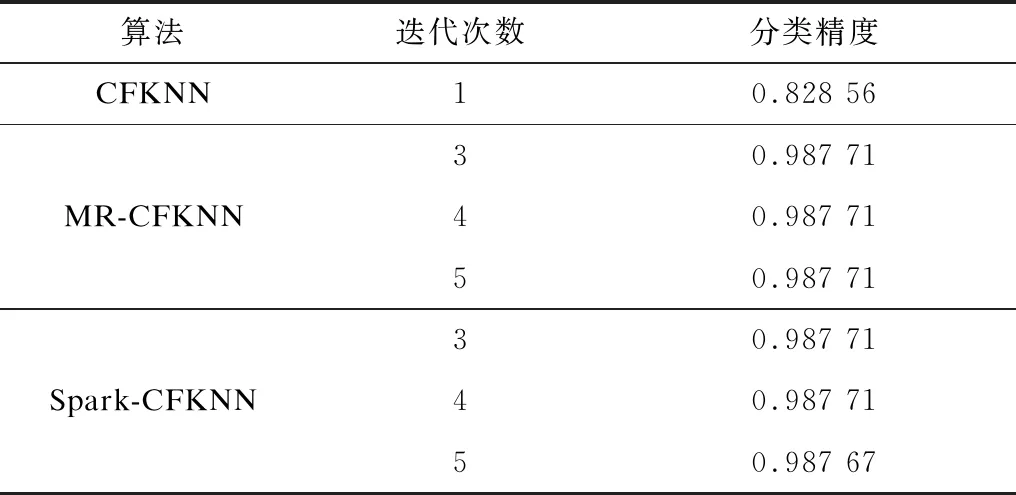
表6 3种算法的分类精度比较

加速比(SpeedUp)是衡量并行计算算法性能和效果的常用指标,传统的加速比计算方式如式(5)所示,其中,Tbest为串行算法在一台计算机上的最优运行时间,T(N)为并行算法在N台计算机上的运行时间。

(5)

由于本文大规模压缩模糊K-近邻算法改变了CFKNN算法对训练集只进行1次迭代的计算方式,因此本文通过式(6)来计算Spark-CFKNN算法的加速比,以此为例来衡量通过大规模压缩模糊K-近邻算法取得的并行化效果,其中,Tsingle-best为Spark-CFKNN算法在单一节点上的最优运行时间。

(6)

表7所示为Spark-CFKNN算法在单一节点和7个节点上的运行时间,从表7可以看出,本文算法大幅缩短了运行时间,具有较高的加速比。

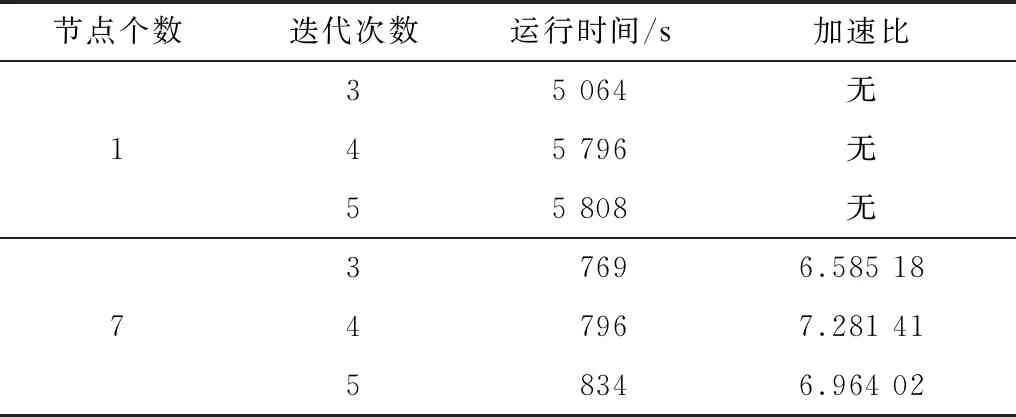
表7 Spark-CFKNN算法在Gaussian1数据集上的加速比

图2所示为不同迭代次数下Spark-CFKNN和MR-CFKNN的分类精度。从图2可以看出,Spark-CFKNN和MR-CFKNN的分类精度变化趋势大致相同,说明2个算法在实现细节上具有逻辑一致性,同时也没有因为平台间运行机制的差异而对分类结果造成影响。此外,由图2可知,分类精度和迭代次数并不成简单的正比关系,即分类精度并不会随着迭代次数的增加而持续增长,当达到一定迭代次数时,分类精度会趋于恒定,这也说明为了提高分类精度而持续增加迭代次数的做法不可行。

图2 Gaussian1数据集上分类精度随迭代次数的变化情况

根据吴信东等人[24]的研究成果,本文对2种大数据平台在不同迭代次数下的文件数目、同步次数和算法运行时间进行对比,结果如表8～表12所示。由于文件数目和同步次数只与大数据平台的调度机制有关而与数据集无关,因此对该指标进行对比时不区分数据集。

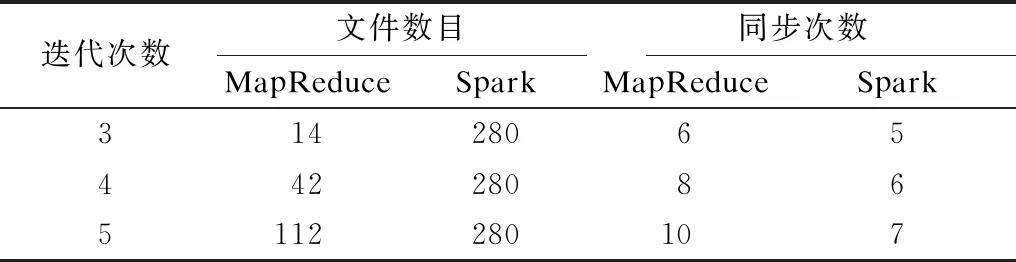
表8 不同迭代次数下文件数目和同步次数的比较

表9 2种平台在Gaussian1数据集下的性能对比

表10 2种平台在Gaussian2数据集下的性能对比

表11 2种平台在Skin Segmentation数据集下的性能对比

表12 2种平台在Healthy Older People数据集下的性能对比

文件数目主要指中间文件数目,因为算法在运行过程中所产生的中间文件数量不仅会占用内存空间,还会影响磁盘的I/O性能,最终导致算法运行时间延长。在MapReduce中,每次的shuffle操作会对map产生的中间结果进行排序和归并操作,MapReduce通过归并和排序操作减少了中间结果传输的数据量,以此保证每一个map只产生一个中间数据文件,达到减少文件数目的目的。在Spark中,默认没有对中间数据进行预排序和归并操作,所以只能将不同分区的数据分别保存在单个文件中,分区个数即为中间文件数目。从表8可以看出,Spark-CFKNN的中间文件数目明显高于MR-CFKNN,且分区数并不随着迭代次数的增加而增加,原因是Spark-CFKNN通过增加分区数目降低了每个分区所需的内存空间,减少了每个task的执行时间,但同时也造成了中间文件数目过多的问题,此外,Spark-CFKNN通过设置Spark的环境变量及对reparation算子进行重分区操作,使得文件数目保持了恒定。

对于同步次数,MapReduce为同步模型,即在所有的map操作结束后才能进行reduce操作。而Spark通过RDD间的宽依赖、窄依赖关系以及管道化操作(pipeline),提高了其并行化程度及Spark中算法的局部性能。

算法的执行时间T会受到输入文件时间Tread、中间数据排序时间Tsort、中间数据传递时间Ttrans和输出文件到HDFS时间Twrite的影响。因为对每一轮的计算结果都进行了广播,2个算法的执行时间差异主要受到MapReduce和Spark运行机制及调度策略的影响,所以最终只考虑Tsort和Ttrans对T造成的影响。对于中间数据排序时间Tsort,由于MapReduce的shuffle过程会对中间结果进行排序和归并操作,因此若假设每个map任务有N条数据,每个reduce任务有M条数据,则MapReduce的中间数据排序时间TMR-sort=N·logaN+R=O(N·logaN)。而在Spark中,默认没有对中间数据进行预排序的操作,因此,Spark的中间数据排序时间TSpark-sort=0。中间数据传递时间Ttrans主要指将map任务运算的数据传送到reduce任务所消耗的时间,Ttrans主要由map任务输出的中间数据大小|D|和网络传输速度Ct所决定。可以看出,在网络传输速度相同的情况下,Ttrans与中间数据大小|D|成正比。由此可知,在相同的迭代次数下,中间数据传递时间Ttrans主要受同步次数的影响。由于Spark引入了管道化操作(pipeline),因此可以减少同步次数,提高并行化程度。由表8中的同步次数可以看出,随着迭代次数的增加,相比MapReduce,Spark在中间数据传递时间Ttrans上的优势越来越明显。

综上,由于MR-CFKNN与Spark-CFKNN算法的程序设计不同,Spark-CFKNN虽然因为增加了分区数而导致Spark的文件数目远多于MapReduce,但因为2个大数据框架的调度机制存在差异,Spark通过引入管道化操作减少了同步次数,使得中间数据传输时间随着迭代次数的增加而越来越优于MapReduce。基于内存的Spark可以将算法运行过程中重复用到的中间数据结果缓存到内存中,减少因为重复计算所消耗的时间,最终使得Spark-CFKNN算法的运行效率优于MR-CFKNN算法。此外,从表9～表12可以看出,Skin Segmentation和Healthy Older People数据集在算法运行时间上的差异小于Gaussian1和Gaussian2数据集,导致该现象的原因是因为前两者的数据规模小于后两者。

分别使用原始数据集和本文算法迭代5次的所选样例集合做训练集,使用KNN算法对分类精度进行测试,结果如表13所示。从表13可以看出,除了Healthy Older People数据集以外,在其余3个数据集上本文算法都实现了精度提升,表明该算法具有有效性。

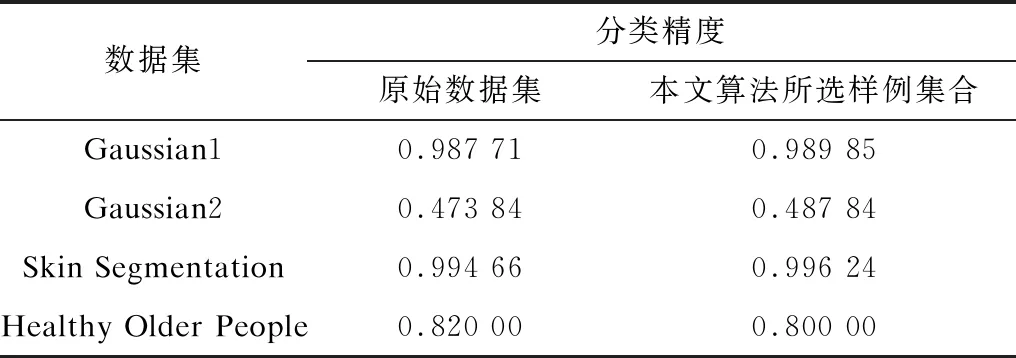
表13 原始数据集和本文算法所选样例集合的最优分类精度对比

4 结束语

本文对CFKNN算法进行改进,提出一种在大数据环境下具有良好可扩展性的大规模压缩模糊K-近邻算法。该算法在样例选择的过程中引入动态机制,使得所选样例更具代表性。实验结果表明,与原始CFKNN算法相比,该算法具有更高的分类精度和加速比,将基于MapReduce和Spark的2种大规模压缩模糊K-近邻算法相比,两者在样例选择个数和分类精度上相近,但在文件数目、同步次数和运行时间上存在比较明显的差异。下一步将对动态选择的阈值是否为最优阈值以及样例初始化是否影响算法性能等问题进行深入研究。