THE EXTENSION OPERATORS ON Bn+1 AND BOUNDED COMPLETE REINHARDT DOMAINS*
Yanyan CUI (崔艳艳)† Chaojun WANG (王朝君)
College of Mathematics and Statistics, Zhoukou Normal University, Zhoukou 466001, China
E-mail : cui9907081@163.com; wang9907081@163.com
Hao LIU (刘浩)
Institute of Contemporary Mathematics, Henan University, Kaifeng 475001, China
E-mail : haoliu@henu.edu.cn
was introduced in [1], where z =(z1,z0)∈ Bn,z1∈ D,z0=(z2,···,zn)∈ Cn−1,f(z1)∈ H(D)and the branch of the square root is chosen such thatThe operator gives a way of extending a univalent analytic function on the unit disc D in C to a biholomorphic mapping on Bn⊂ Cn. Roper and Suffridge [1]proved that Φn(K) ⊆ K(Bn). Graham and Kohr [2]proved that the Roper-Suffridge operator preserves the properties of Bloch mappings on Bnand Φn(S∗)⊆ S∗(Bn), and generalized the Roper-Suffridge operator to be
The above conclusions illustrate that the Roper-Suffridge operator and its extensions are the links between starlike (respectively convex) functions on D and starlike (respectively convex)mappings on Bn. Starlike mappings and convex mappings are important research objects in the geometric function theory of several complex variables. It is easy to find the concrete starlike or convex functions on D, while it is difficult in Cn. By using the Roper-Suffridge operator and its extensions we can construct lots of concrete starlike or convex mappings in Cnfrom the corresponding functions on D. Therefore the Roper-Suffridge operator is useful and important for studying biholomorphic mappings with particular geometric properties in Cn.
Pfaltzgraff and Suffridge [3]introduced the operator
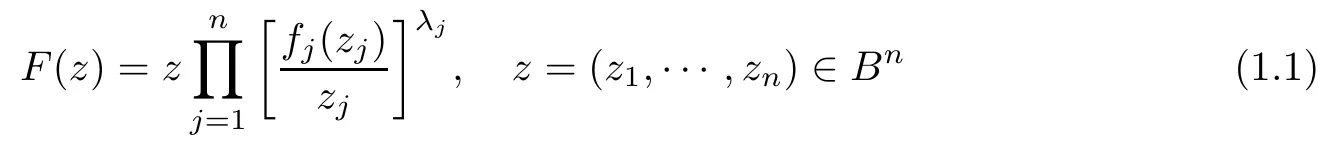
on the Euclidean unit ball of Cn, where λj≥ 0 and
Gong,Liu[4]and Liu,and Liu[5]generalized the Roper-Suffridge operator on more general Reinhardt domains and researched the behaviours of the extension operators. Liu [6]extended the operator (1.1) on bounded starlike circular domains to be
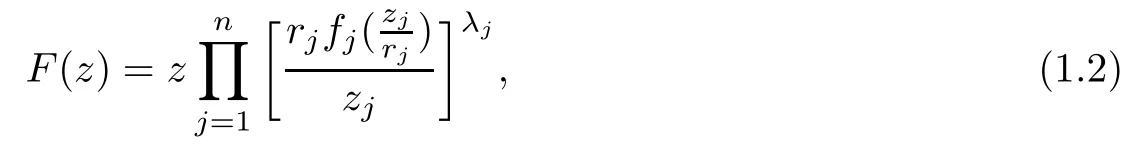
and proved that the operator(1.2)preserves(almost)starlikeness of order α on bounded starlike circular domains.
Duan [7]obtained that the generalized operator
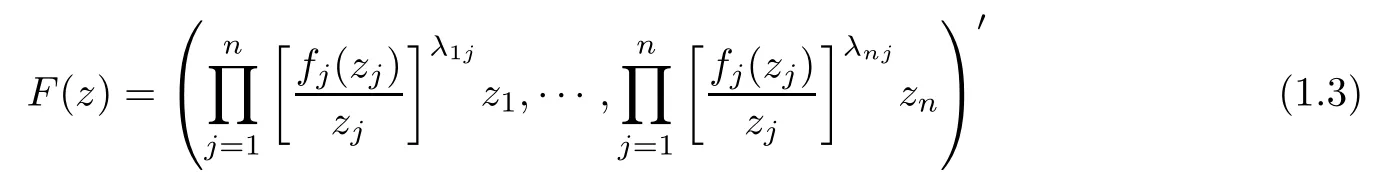
preserves starlikeness on the unit ball Bnin Cn, where Λ = (λij) and Λ is invertible, λij≥ 0,In recent years, there have appeared many results about generalized Roper-Suffridge operators (see [8–11]).
The above operators all construct locally biholomorphic mappings on different domains in Cnfrom one locally biholomorphic function or n functions f1,··· ,fnin C, while the operator
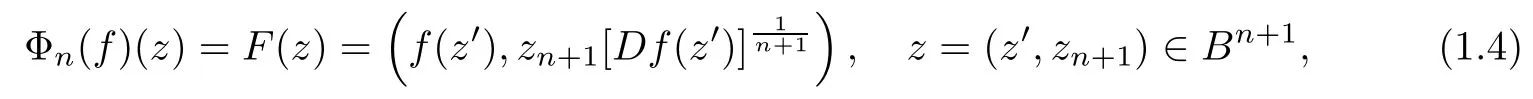
introduced by Pfaltzgraff and Suffridge [12], constructs F ∈H(Bn+1) from a locally biholomorphic function f ∈ H(Bn), where n ≥ 1, z′= (z1,··· ,zn) ∈ CnandLetting f(z′)=(f1(z1),··· ,fn(zn)), the operator(1.4)constructs F ∈ H(Bn+1)from n locally biholomorphic functions fi∈ H(D)(i = 1,··· ,n). This stimulates us to extend the Roper-Suffridge operator to be

where z = (z1,··· ,zn+1) ∈ Bn+1, n ≥ 1, fj(zj) (j = 1,··· ,n) is a normalized locally biholomorphic function on D withfor zj∈ D{0}. For n=1 the operator(1.5)reduces to Φ2,β,as introduced by Graham and Kohr in [2]. The operator (1.5) is not the special form of (1.1) and (1.3); we will shortly investigate the behaviours of (1.5) on Bn+1.
On the bounded complete Reinhardt domain Ω ⊂ Cn+1, we introduce the following extension operator:

where rj=sup{|zj|:(z1,··· ,zj,··· ,zn+1)′∈ Ω}is a normalized locally biholomorphic function on D withfor zj∈D{0}. The operator (1.6) is not the special form of (1.2). Applying (1.5) and (1.6),we can construct biholomorphic mappings in Cn+1(not in Cn) from biholomorphic functions f1,··· ,fnin C.
In this article, we investigate the properties of the generalized operators(1.5)and(1.6). In section 3, we discuss the fact that the mapping defined by (1.5) has parametric representation on Bn+1if fi(i = 1,··· ,n) does on D, and we research the geometric invariance of some subclasses of spirallike mappings preserved by (1.5) on Bn+1. In section 4, from the geometric characteristics and the parametric representation of subclasses of spirallike mappings,we obtain that (1.6) preserves the geometric properties of several subclasses of spirallike mappings on bounded complete Reinhardt domains in Cn+1.
2 Definitions and Lemmas
In what follows, let D denote the unit disk in C, Bndenote the unit ball in Cn, and H(Ω)denote the holomorphic mappings on Ω. Let DF(z) denote the Fréchet derivative of F at z.
To obtain the main results, we need the following definitions and lemmas:
Definition 2.1([13]) A mapping f : Bn× [0,∞) → Cnis called a Loewner chain if it satisfies the following conditions:
(1) f(·,t) is biholomorphic on Bn, f(0,t)=0, Df(0,t)=etIn(t ≥ 0);
(2) f(z,s)≺ f(z,t) whenever ∀ 0 ≤ s ≤ t< ∞ and z ∈ Bn; that is, there exists a Schwarz mapping v =v(z,s,t) such that
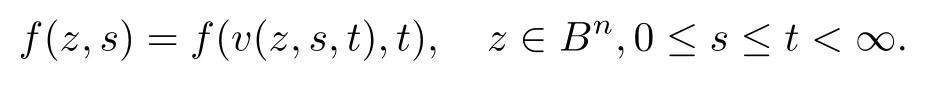
Definition 2.2([13]) Let f(z) be a normalized biholomorphic mapping on Bn. We say that f(z) has parametric representation on Bnif there is a Loewner chain f(z,t) such that{e−tf(·,t)}t≥0is a normal family on Bnand f(z)=f(z,0)(z ∈ Bn).
Definition 2.3([14]) Let F(z) be a normalized locally biholomorphic mapping on Bn,and α ∈ [0,1), β ∈c ∈ (0,1). Then F(z) is called a strong and almost spirallikemapping of type β and of order α on Bnprovided that

If we define strong and almost spirallike mappings of type β and of order α on bounded complete Reinhardt domains, the corresponding condition is
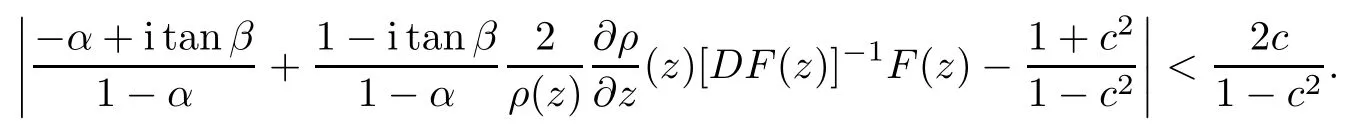
Setting α = 0, β = 0 and α = β = 0, Definition 2.3 reduces to the definition of strong spirallike mappings of type β, strong and almost starlike mappings of order α, and strong starlike mappings, respectively.
Definition 2.4([15]) Let Ω ⊂ Cnbe a bounded starlike circular domain whose Minkowski functional ρ(z)is C1except for a lower-dimensional manifold. Let F(z)be a normalized locally biholomorphic mapping on Ω. Then we say thatprovided that
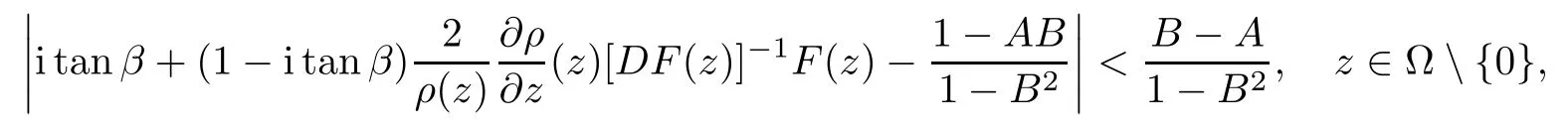
where −1 ≤ A
Setting A = −1 = −B − 2α, A = −B = −α, B → 1−in Definition 2.4, we obtain the corresponding definitions of spirallike mappings of type β and order α [16], strongly spirallike mappings of type β and order α [17], and almost spirallike mappings of type β and order α [18]on Ω, respectively.
Definition 2.5([19]) Let Ω ⊂ Cnbe a bounded starlike circular domain whose Minkowski functional ρ(z)is C1except for a lower-dimensional manifold. Let F(z)be a normalized locally biholomorphic mapping on Ω. Then F(z)is called an almost starlike mapping of complex order λ on Ω provided that
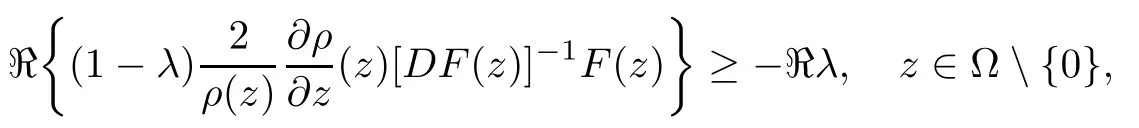
where λ ∈ C,ℜλ ≤ 0.
Setting∈ [0,1) in Definition 2.5, we obtain the definition of almost starlikemappings of order α on Ω.
Definition 2.6([20]) Let Ω ⊂ Cnbe a bounded starlike circular domain whose Minkowski functional ρ(z)is C1except for a lower-dimensional manifold. Let F(z)be a normalized locally biholomorphic mapping on Ω and let ρ ∈ [0,1), β ∈Then F(z) is called a parabolic and spirallike mapping of type β and of order ρ on B provided that
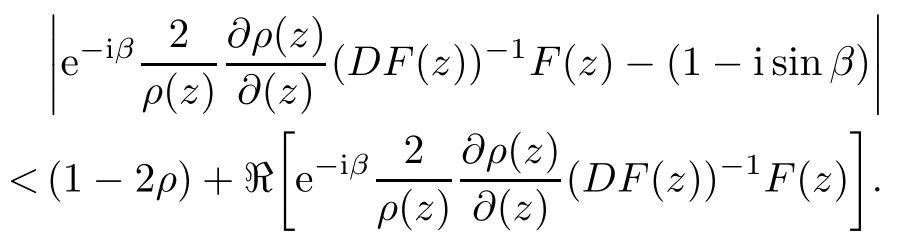
Suffridge [21]introduced the definition of spirallike mappings with respect to a normal linear operator A whose eigenvalues have a positive real part in complex Banach spaces. Now we extend the definition on bounded complete Reinhardt domains.
Definition 2.7Let A ∈L(Cn+1,Cn+1) be a continuous complex-linear operator with
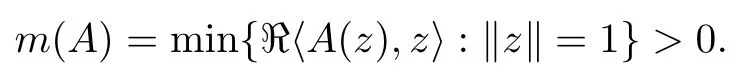
Let Ω ⊂ Cn+1be a bounded complete Reinhardt domain and let f :Ω → Cn+1be a normalized locally biholomorphic mapping. Then f is spirallike relative to A if
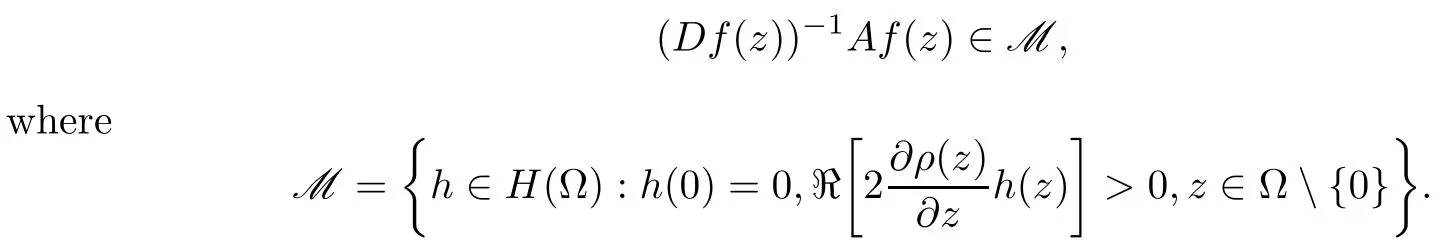
Lemma 2.8([22]) Let f(z) be a normalized locally biholomorphic mapping on B withand a = tan β. Then f(z) is an almost spirallike mapping of order α and of type β on B if and only if g(z,t)=is a Loewner chain.
Lemma 2.9([13]) Let f(z,t) be a Loewner chain. Then

Lemma 2.10([23]) Let Ω ⊂ Cn+1be a bounded complete Reinhardt domain whose Minkowski functional ρ(z) is C1except for a lower-dimensional manifold. Then we have
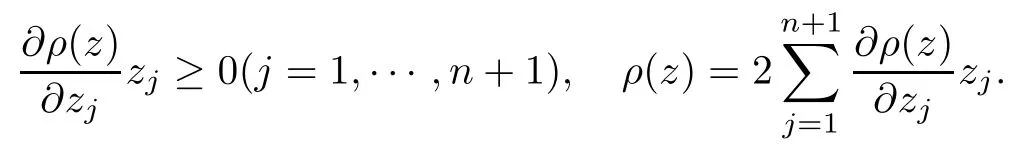
Lemma 2.11([24]) Let Ω ⊂ Cnbe a bounded complete Reinhardt domain and let h ∈M, where

Then the initial value problem

has a unique solution v(t) = v(z,t) (t ≥ 0). Furthermore, v(z,t)→ 0 (t → +∞) and v(z,t) is a Schwarz mapping on Ω for fixed t.
Lemma 2.12([25]) Let Ω ⊂ Cnbe a bounded starlike circular domain and let h ∈M, Jh(0) = A, v(z,t) be a solution of the initial value problem (2.1). Then for ∀z ∈ Ω,must be existing and converge to a spirallike mapping relative to A on Ω. If,instead, f(z) is a spirallike mapping relative to A on Ω and Jf(z)h(z)= Af(z), f(z) must be expressed as
3 Extension Operators on the Unit Ball Bn+1
In this section we will investigate the properties of mappings constructed by (1.5) on the unit ball Bn+1in Cn+1(not in Cn) from biholomorphic functions f1,··· ,fnin C.
Theorem 3.1Suppose that the normalized biholomorphic function fk(zk) can be embedded in Loewner chain {gk(zk,t)}t≥0(k = 1,··· ,n) on D. Then the mapping F(z) defined by (1.5) can be embedded in a Loewner chain on Bn+1.
ProofAs fk(zk)is the normalized biholomorphic function on D,then F(z)is normalized biholomorphic on Bn+1obviously. Because fk(zk) can be embedded in the Loewner chain{gk(zk,t)}t≥0, there exists a Schwarz mapping vk=vk(zk,s,t) such that

(i) As {gk(zk,t)}t≥0is a Loewner chain, gk(·,t) is biholomorphic on D and gk(0,t) = 0,Therefore F(z,t) is biholomorphic on Bn+1. By a simple calculation we obtain that F(0,t)=0,DF(0,t)=etIn+1where In+1is the identity operator in Cn+1.
(ii) Let

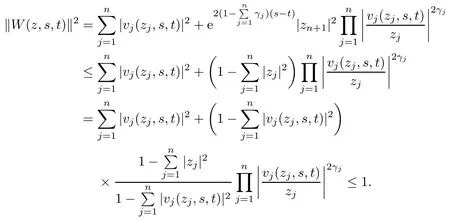
Thus W(z,s,t) is a Schwarz mapping on Bn+1.
(iii) In view of (3.1) and (3.2), we obtain
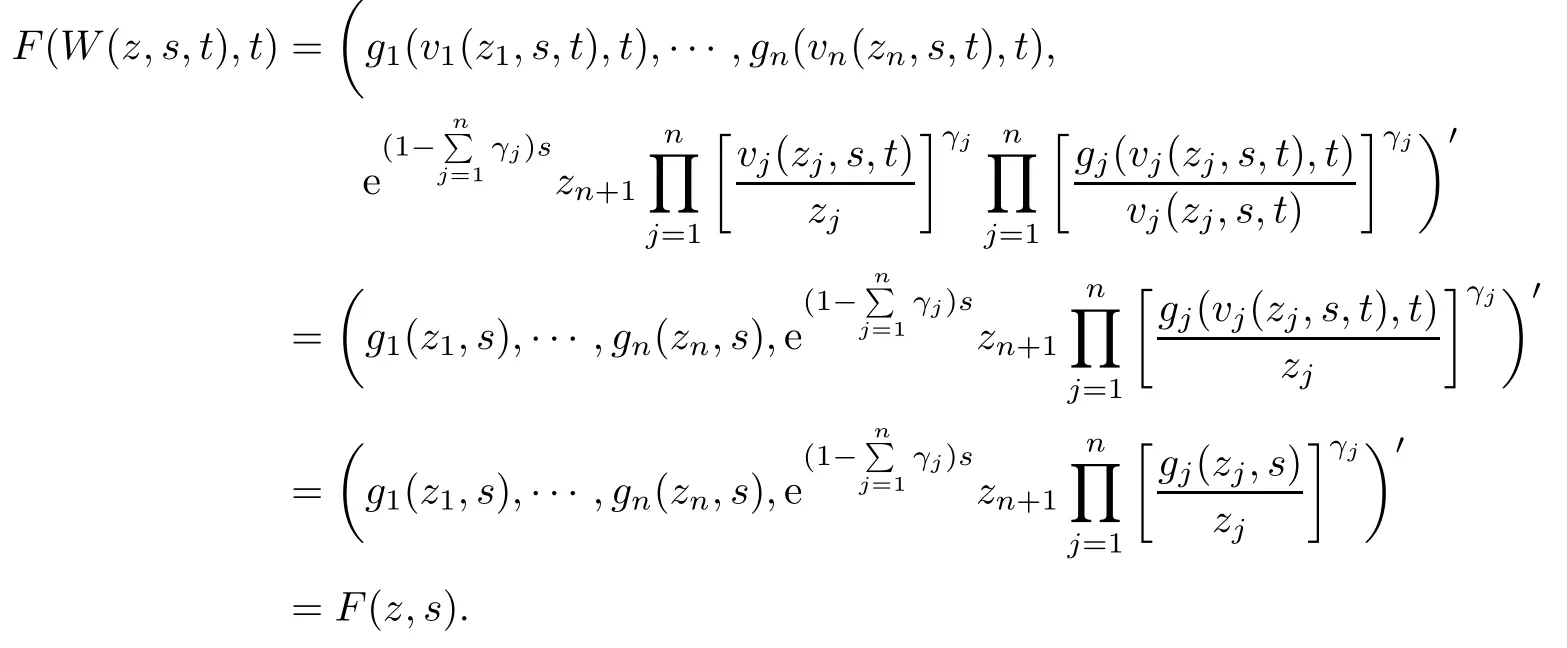
From(i)–(iii)and Definition 2.1 we obtain that F(z,t)is a Loewner chain. As fk(zk)can be embedded in the Loewner chain{gk(zk,t)}t≥0,gk(zk,0)=fk(zk),and therefore F(z,0)=F(z).Hence F(z) can be embedded in the Loewner chain F(z,t) on Bn+1.
Theorem 3.2Suppose that fk(zk)(k =1,··· ,n) is an almost spirallike function of type β and of order α on D with α ∈ [0,1), β ∈Then F(z) defined by (1.5) is an almost spirallike mapping of type β and of order α on Bn+1.
ProofFrom (1.5) we obtain

As fk(zk)is an almost spirallike function of type β and of order α on D,gk(zk,t)is the Loewner chain in which fk(zk) is embedded. By (3.3) and (3.4), we obtain
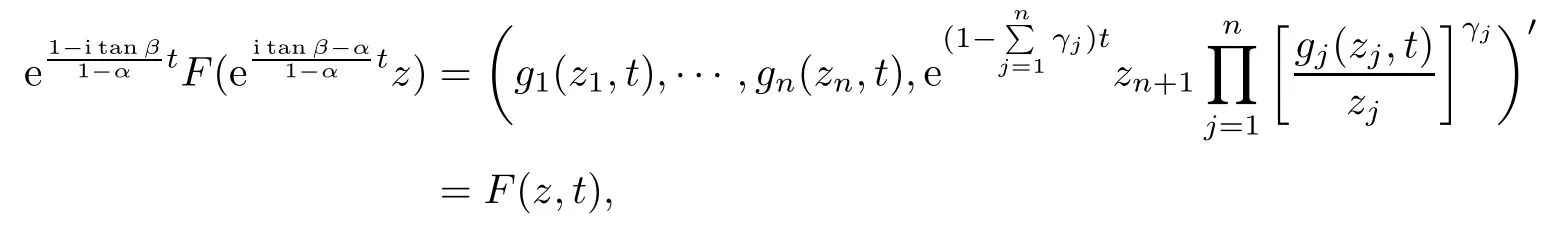
where F(z,t)is the mapping defined by(3.2)in Theorem 3.1,and thereforeis a Loewner chain. By Lemma 2.8 we obtain that F(z)is an almost spirallike mapping of type β and of order α on Bn+1.
Theorem 3.3If fk(zk) (k = 1,··· ,n) has parametric representation on D, then F(z)defined by (1.5) has parametric representation on Bn+1.
ProofAs fk(zk) has parametric representation on D, there exists a Loewner chain gk(zk,t) such that gk(zk,0) = fk(zk), and {e−tgk(·,t)}t≥0is a normal family. By Lemma 2.9 we obtain

Therefore, for |zk| By Theorem 3.1 we obtain that F(z,t)defined by(3.1)is a Loewner chain,that F(z,0)=F(z)and Therefore {e−tF(·,t)}t≥0is locally uniformly bounded on Bn+1, and thus is a normal family.By Definition 2.2 we obtain that F(z) has parametric representation on Bn+1. Theorem 3.4Suppose that fk(zk) (k =1,··· ,n) is a strong and almost spirallike function of type β and of order α on D with α ∈ [0,1) and β ∈Then F(z) defined by(1.5) is a strong and almost spirallike mapping of type β and of order α on Bn+1. ProofBy (1.5) we obtain As fj(zj) (j =1,··· ,n) is normalized locally biholomorphic on D withandis normalized locally biholomorphic on Bn+1and By Definition 2.3, we need only to prove that Then |qk(zk)|<1. In view of c ∈(0,1) and (3.5), we obtain Therefore F(z) is a strong and almost spirallike mapping of type β and of order α on Bn+1by Definition 2.3. Similarly to Theorem 3.4 we can obtain the following conclusion: Theorem 3.5Let(k = 1,··· ,n) with −1 ≤A < B < 1 andLetting F(z)be the mapping defined by(1.5),we get that F(z)∈ Remark 3.6Setting β = 0 (respectively α = 0) in Theorem 3.4, we obtain the corresponding results for strong and almost starlike mappings of order α (and, respectively,the strongly spirallike mappings of type β). Setting A = −1 = −B − 2α (respectively,A = −B = −α) in Theorem 3.5, we obtain the corresponding results for spirallike mappings of type β and of order α (and, respectively, the strongly spirallike mappings of type β and of order α). Theorem 3.7Let fk(zk) (k =1,··· ,n) be an almost starlike function of complex order λ on D with λ ∈ C,ℜλ ≤ 0. Then F(z) defined by (1.5) is an almost starlike mapping of complex order λ on Bn+1. ProofBy Definition 2.5, we need only to prove that As fk(zk) is an almost starlike function of complex order λ on D, by Definition 2.5, we have that Then ℜpk(zk)≥ 0. By (3.5) we obtain that In addition, ℜpk(zk) ≥0 implies thatTherefore F(w,z) is an almost starlike mapping of complex order λ on Bn+1. Remark 3.8Settingin Theorem 3.7, we obtain the corresponding results for almost starlike mappings of order α. Let Ω ⊂ Cn+1be a bounded starlike circular domain whose Minkowski functional ρ(z) is C1except for a lower-dimensional manifold. In this section we will study the properties of(1.6), preserving several subclasses of spirallike mappings on Ω. Theorem 4.1Let(k = 1,··· ,n) with −1 ≤A < B < 1 andLet F(z) be the mapping defined by (1.6). Then ProofBy Definition 2.4, we need only to prove that Then |qk(ξk)|<1. By (4.2) we obtain that which follows (4.1). By Definition 2.4 we obtain that Similarly, we can obtain that F(z) defined by (1.6) preserves the strongth and almost spirallikeness of type β and of order α on Ω. Theorem 4.2Let(k = 1,··· ,n) be a strong and almost spirallike function of type β and of order α on D with α ∈ [0,1) andThen F(z) defined by (1.6) is a strong and almost spirallike mapping of type β and of order α on Ω. Remark 4.3Setting A= −1= −B −2α (respectively, A= −B = −α) in Theorem 4.1,we obtain the corresponding results for spirallike mappings of type β and of order α (respectively,the strongly spirallike mappings of type β and of order α). Setting β =0 (respectively, α =0)in Theorem 4.2, we obtain the corresponding results for strong and almost starlike mappings of order α (and respectively, the strongly spirallike mappings of type β). Theorem 4.4Let(k =1,··· ,n) be a parabolic and spirallike function of type β and of order ρ on D with ρ ∈ [0,1), β ∈and ρ ≤ cos β. Then F(z) defined by (1.6) is a parabolic and spirallike mapping of type β and of order ρ on Ω. ProofBy Definition 2.6, we need only to prove that As fk(ξk) is a parabolic and spirallike function of type β and of order ρ on D, we have that By (4.2) we obtain that In view of ρ ≤ cos β, by (4.4) we obtain that which follows(4.3). Therefore F(z)is a parabolic and spirallike mapping of type β and of order ρ on Ω. Remark 4.5Setting ρ = 0 (respectively, β = 0) in Theorem 4.4, we obtain the corresponding results for parabolic and spirallike mappings of type β (respectively, the parabolic and starlike mappings of order ρ). Similarly to Theorem 4.4, we can obtain the following conclusion: Theorem 4.6Let(k =1,··· ,n) be an almost starlike function of complex order λ on D with λ ∈ C,ℜλ ≤ 0. Then F(z) defined by (1.6) is an almost starlike mapping of complex order λ on Ω. For rj=1 (j =1,··· ,n), (1.6)reduces to(1.5). Therefore,from the above conclusions,we can obtain that (1.5) preserves the properties of the following biholomorphic mappings on the Reinhardt domain: Corollary 4.7Let fk(zk)be a strong and almost spirallike function of type β and of order α on D (respectively,a parabolic and spirallike function of type β and of order ρ,and an almost starlike function of complex order λ). Then F(z)defined by(1.5)is a strong and almost spirallike mapping of type β and of order α on Ωn+1,p(respectively,a parabolic and spirallike mapping of type β and of order ρ, and an almost starlike mapping of complex order λ). Remark 4.8For pn+1= 2, Ωn+1,preduces to Bn+1. Therefore, by corollary 4.7 we obtain the corresponding results for (1.5) on Bn+1. In what follows we will research the properties of the operator(1.6)on the bounded complete Reinhardt domain Ω from the parametric representation of spirallike mappings. Theorem 4.9Let(k =1,··· ,n)be a spirallike function relative to A on D with A being a continuous complex-linear operator. Then F(z)defined by(1.6)is a spirallike mapping relative to A on Ω, where Proof(i) Asis a spirallike function relative to A on D, there existssuch that Let F(z)=(F1(z),··· ,Fn+1(z)). For z ∈ Ω we have that By (4.7) and (4.9), we obtain that−H(u(z,t)), where Furthermore, that is,u(z,0)=z. Therefore u(z,t)is the solution of the initial value problem(2.1)in Lemma 2.11. (iii) In view of hj∈M and (4.8), we have that Applying Lemma 2.10, we obtain that so H ∈M. By (4.5) we have that By simple calculation, we obtain that For H(u(z,t))=(u1q1(u),··· ,un+1qn+1(u))′, let Hj(u)=ujqj(u) (j =1,··· ,n+1). By (4.8)we get thatfor j =1,··· ,n, therefore By (4.9) we get that By (4.11)–(4.13) we obtain that JH(0)=A. From (i)–(iii) and lemma 2.12 we obtain that F(z) is a spirallike mapping relative to A onΩ. Corollary 4.10Let(k = 1,··· ,n) be a spirallike function relative to A on D.Then is a spirallike mapping relative to A on Ω, where Remark 4.11Setting A=e−iβIinto Theorem 4.9 and Corollary 4.10, we obtain the corresponding results for spirallike mappings of type β.
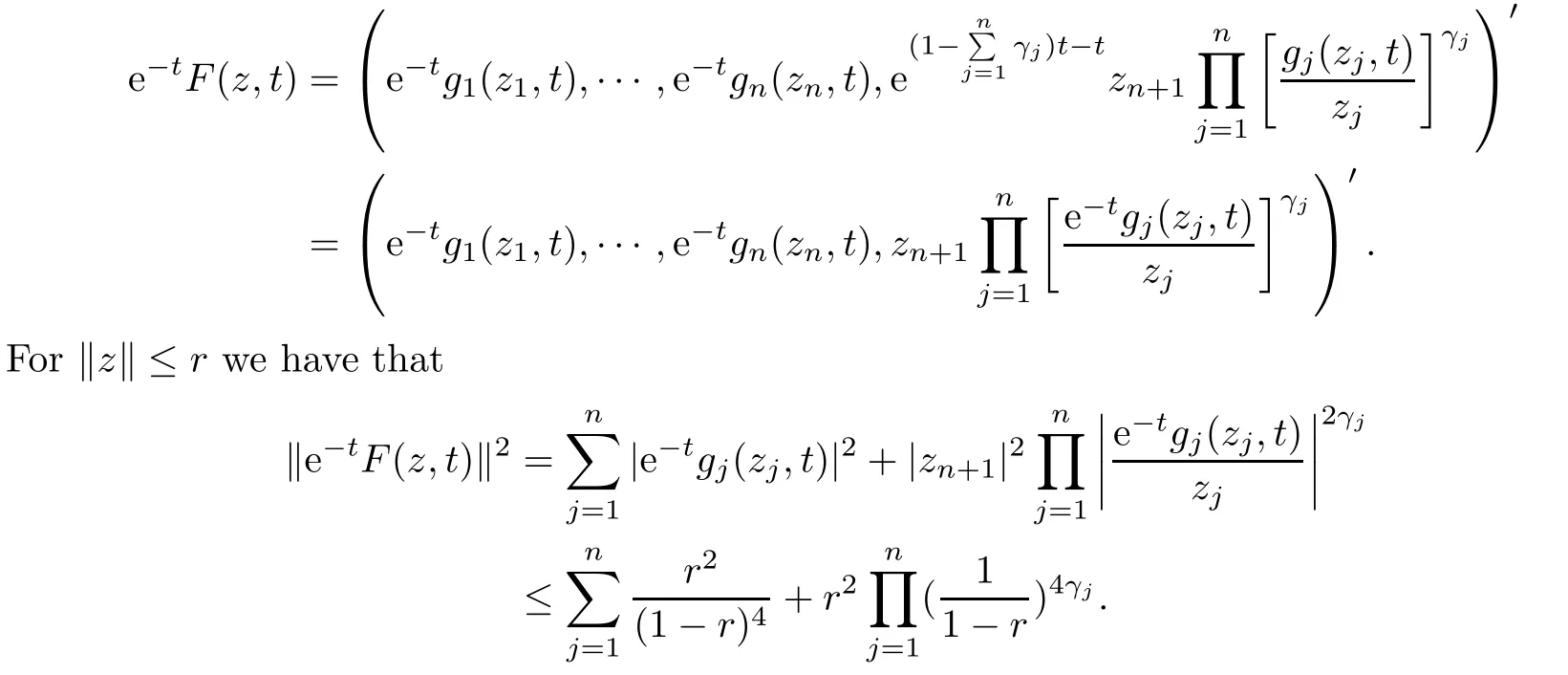
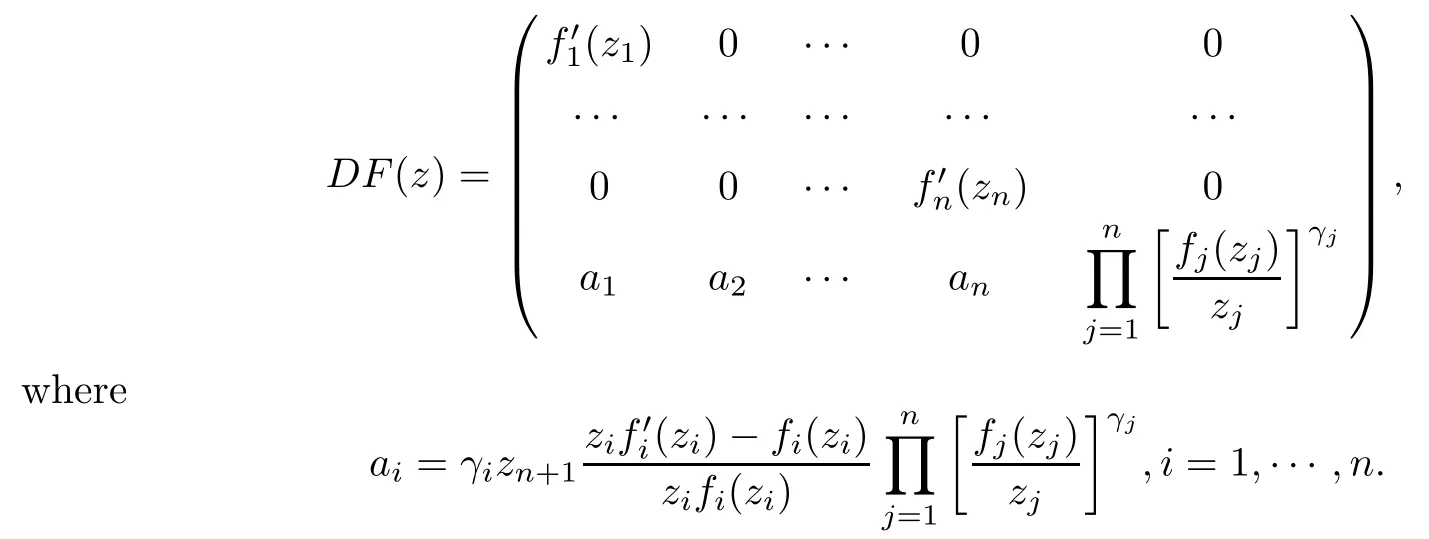
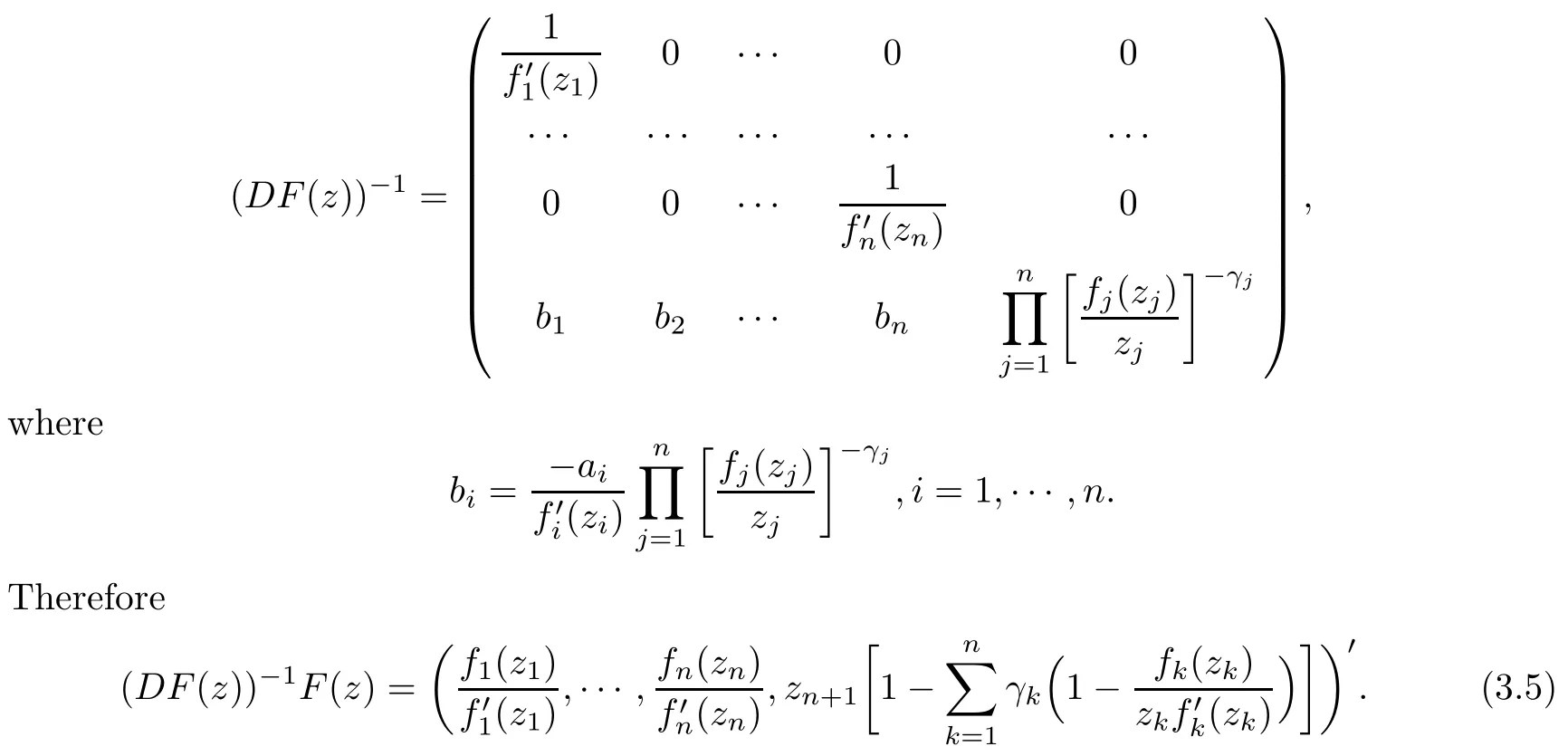


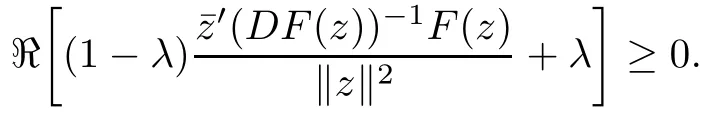
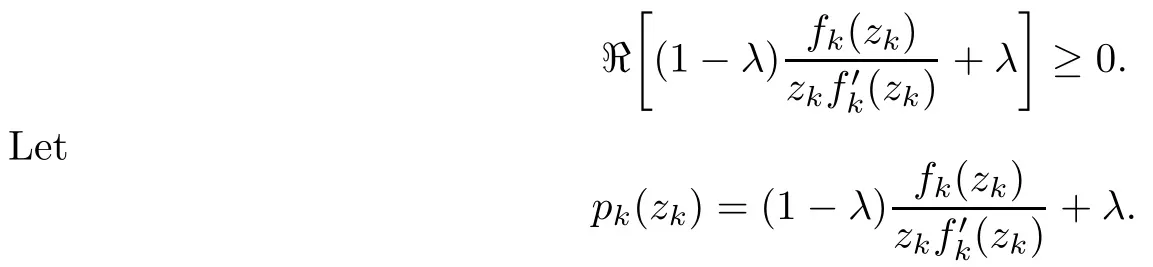
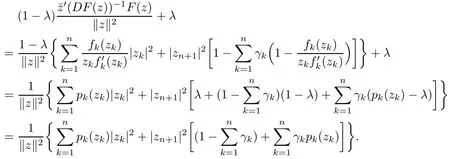
4 Extension Operators on Bounded Complete Reinhardt Domains
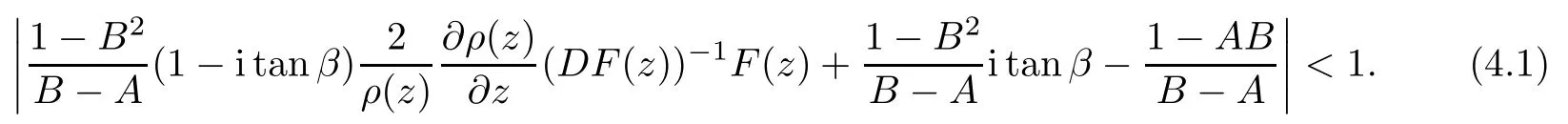

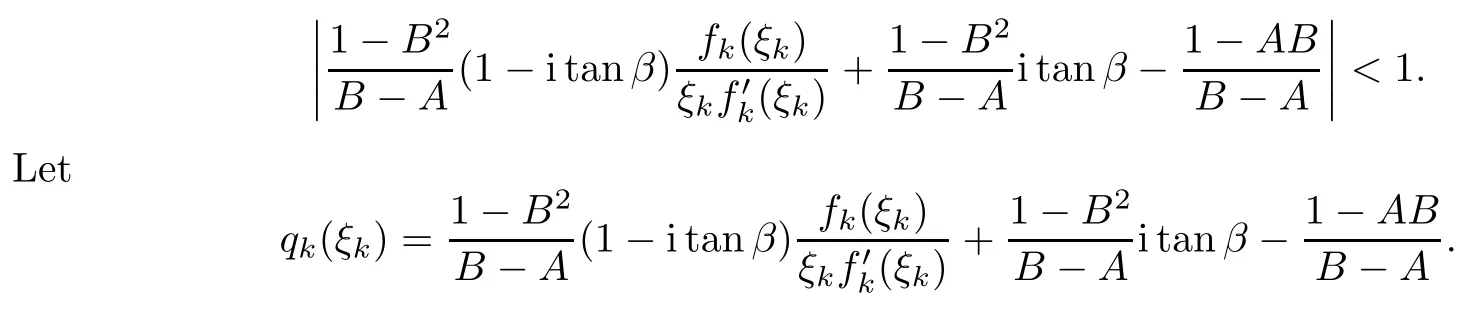

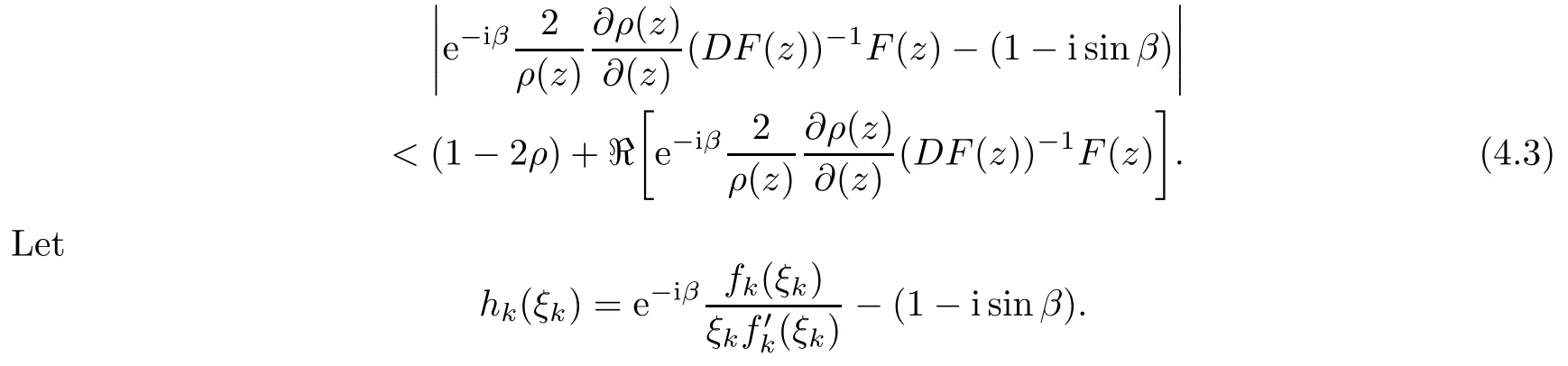
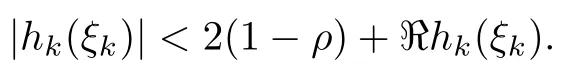


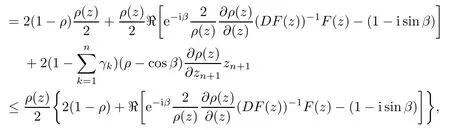
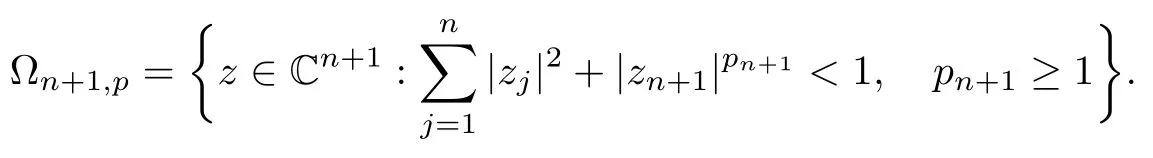

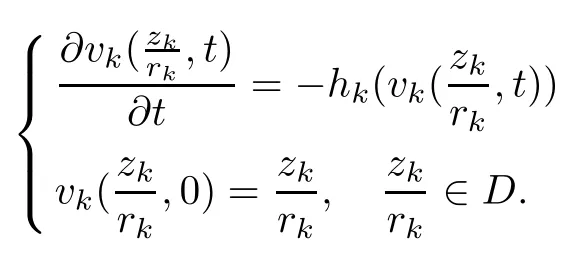



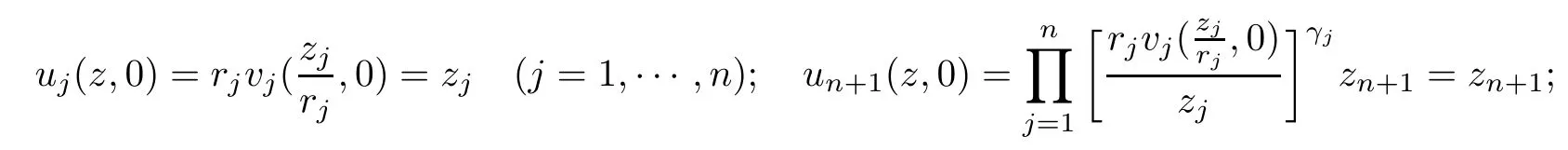
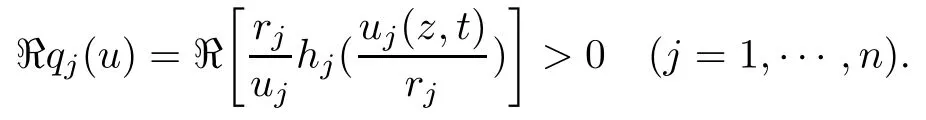
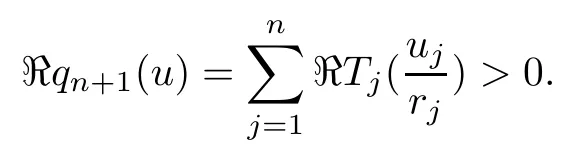
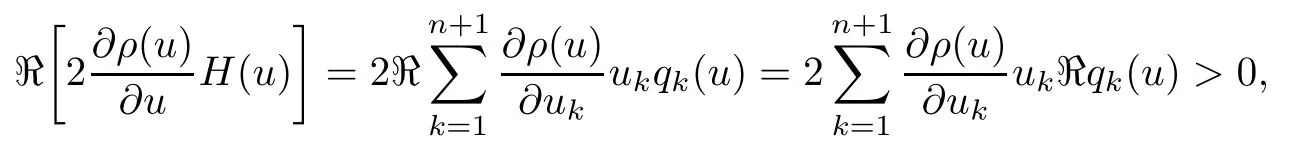

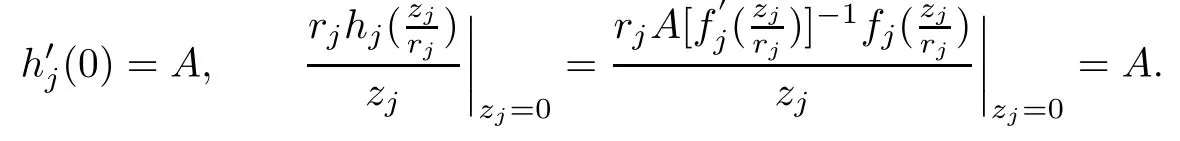
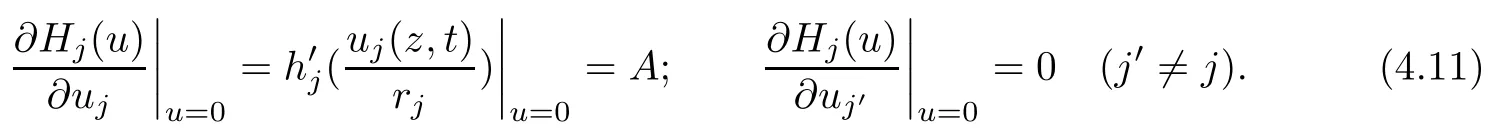
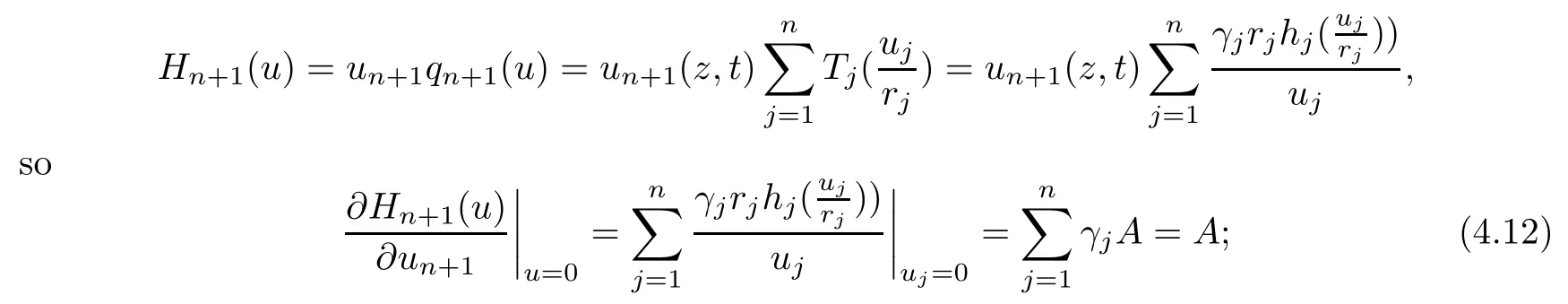



 Acta Mathematica Scientia(English Series)2020年5期
Acta Mathematica Scientia(English Series)2020年5期
- Acta Mathematica Scientia(English Series)的其它文章
- RETRACTION NOTE: “MINIMAL PERIOD SYMMETRIC SOLUTIONS FOR SOME HAMILTONIAN SYSTEMS VIA THE NEHARI MANIFOLD METHOD”Acta Mathematica Scientia, 2020,40B(4):614–624
- DYNAMIC ANALYSIS AND OPTIMAL CONTROL OF A FRACTIONAL ORDER SINGULAR LESLIE-GOWER PREY-PREDATOR MODEL∗
- POSITIVE SOLUTIONS AND INFINITELY MANY SOLUTIONS FOR A WEAKLY COUPLED SYSTEM∗
- PARAMETERS IDENTIFICATION IN A SALTWATER INTRUSION PROBLEM∗
- A LEAST SQUARE BASED WEAK GALERKIN FINITE ELEMENT METHOD FOR SECOND ORDER ELLIPTIC EQUATIONS IN NON-DIVERGENCE FORM∗
- EXISTENCE AND CONCENTRATION BEHAVIOR OF GROUND STATE SOLUTIONS FOR A CLASS OF GENERALIZED QUASILINEAR SCHRDINGER EQUATIONS IN RN∗
