灰色预测模型在公共卫生事件胜利日预测中的应用——以新型冠状病毒疫情为例

赵露露，李 星，金新政

(华中科技大学同济医学院医药卫生管理学院，湖北 武汉 430030)

冠状病毒是一个大型病毒家族，已知可引起感冒、中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病[1]。新型冠状病毒是以前从未在人体中发现的冠状病毒新毒株，可以在人与人之间传染，主要的传播途径是呼吸道飞沫传播和接触传播，各个年龄段的人均易感。

2019年12月，湖北省武汉市发现多起新冠肺炎感染者，随后新冠肺炎开始在武汉市内大范围的传播、爆发。随之，中国其他地区也出现感染者。截至2020年6月，国内新冠肺炎疫情已经得到了很好的控制。但是，此次新冠肺炎疫情对我国人民的生活和经济发展造成了严重的影响。此类突发公共卫生事件具有波及方式多元、规模大、危害性严重等特点[2]。数学建模对传染病传播过程的描述、分析、预报和控制能起到积极的作用，为降低以后此类突发公共卫生事件对人民生活和社会经济的影响程度，有必要对新冠肺炎疫情数据建模后进行回顾性分析。鉴于新冠肺炎是一种新型的传染病，对它知之甚少，在前期不可能拥有太多的案例的情况下，本研究采用灰色模型的思想来对其数据进行建模预测，事实证明，灰色预测模型在此类突发公共卫生事件的预测中具有较高的准确性，现将具体研究情况报告如下。

1 数据与方法

1.1 数据来源

从国家卫生健康委员会官方网站[3]选取2020年2月6日-4月2日全国(除湖北省外)每日本土新增的新型冠状病毒感染的肺炎患者数据，数据真实可靠、可信度高。

1.2 研究方法

本文采用灰色预测模型中的GM(1，1)模型来预测传染病病毒感染的患者人数的变化[4]，主要是预测该传染病病毒感染的患者人数为零的时间点，即“胜利日”的具体时间，并与实际“胜利日”数据做对比，以分析GM(1，1)模型在预测此类突发公共卫生事件受感染患者人数是否具有科学性。

1.3 模型构建

GM(1，1)模型中的两个“1”分别代表的是模型中包含1个变量，且这个变量近似符合1阶线性微分方程[5]。建立GM(1，1)模型的具体步骤如下：

首先确定原始的数据组，假设原始数据组包括n个数据，那么数据可以表示为：

X(0)={X(0)(1),X(0)(2),X(0)(3)…X(0)(n)}

(1)

然后假设X(1)为X(0)做1-AGO生成得到的数据组，则X(1)表示为：

X(1)={X(1)(1),X(1)(2),X(1)(3)…X(1)(n)}

(2)

接下来用X(0)与X(1)来建立矩阵B和YN矩阵，具体计算方法如下：

(3)

(4)

然后使用最小二乘法，通过B和YN计算出a和b：

(5)

接着将a和b代入时间序列方程之中，这样就可以得到GM(1，1)模型的方程：

(6)

最后，可以通过下列式子计算出相应的模型预测值：

(7)

1.4 模型精度测试

为了检验GM(1，1)模型的精准性，需要对该模型的精度进行测试，主要包括小误差概率P和后验差比值C，首先计算小误差概率P。

假设该模型的残差为F(K)，也就是实际值与预测值之差：

(8)

同时，计算出原数据组X(0)的方差S0：

(9)

然后根据残差的方差S0乘以0.6745确定一个标准，小误差概率P计算的就是残差与残差平均值差的绝对值落在这个标准内的概率：

(10)

然后计算后验差比值C，根据数据的残差F(K)，计算出残差的方差S1，再根据后验差比值等于原数据的方差除以残差的方差，计算出C：

(11)

(12)

计算出来的后验差比值C与小误差概率P，结合拟合等级检验评判表(见表1)，可以判断模型的拟合等级，以此为依据来检验该模型是否具有科学性，以及是否可以外推用于预测。

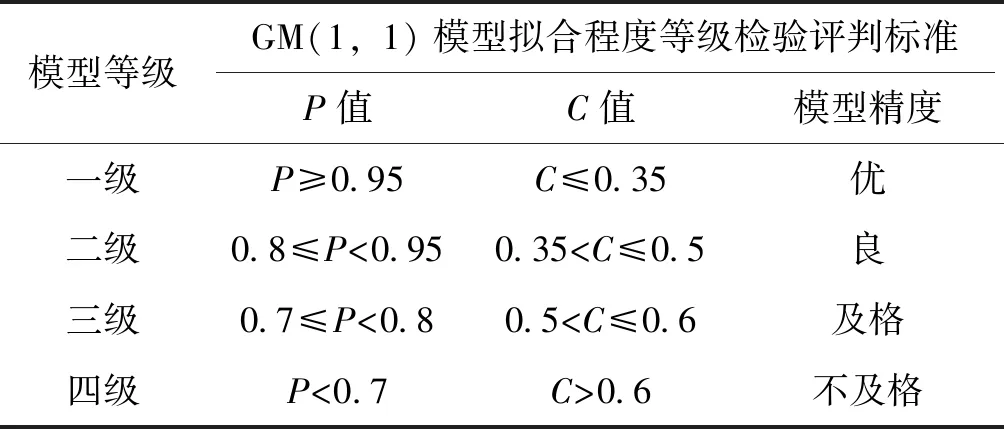
表1 GM(1，1)模型拟合程度等级检验评判表

2 实证分析

2.1 建立灰色系统动态模型

全国(除湖北省外)2月6-10日新型冠状病毒感染的肺炎每日新增确诊病例数(见表2)为原始数据X(0)：X(0)={X(0)(1)，X(0)(2) ，X(0)(3)，X(0)(4)}=(696， 558， 509， 444， 381)；对原始数据X(0)处理累加得X(1)：X(1)={X(1)(1)，X(1)(2) ，X(1)(3)，X(1)(4)}=(1254， 1763， 2207， 2588)；接下来结合公式(5)及相应数据计算出参数a=-0.1248554，b=687.3141；将X(0)(1)、a、b等带入公式计算，最终得新型冠状病毒肺炎感染的患者每日新增确诊病例数GM(1，1)灰色预测模型X(1)(k+1)=5,504.88-480,888e-0.124855k。根据所得预测模型测得2月6-18日全国(除湖北省外)新型冠状病毒感染的肺炎确诊病例数，并与2月6-18日全国(除湖北省外)新型冠状病毒肺炎病例实际数值进行比较，计算得出残差和相对误差，相关数据见表3。

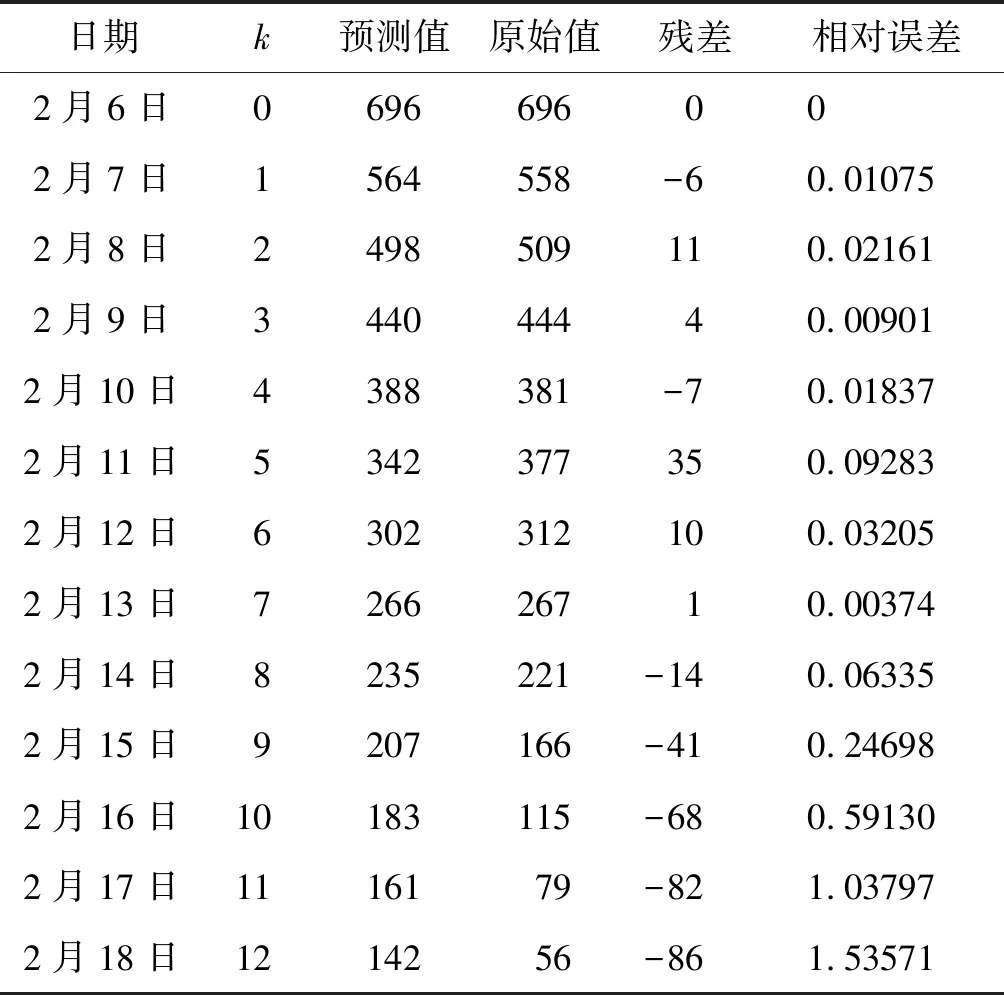
表3 全国(除湖北省外)2020年2月6-18日

2.2 模型检验与分析

为了检测模型的精度，根据GM(1，1)模型精度评判标准计算后验差比值C和小误差概率P来判断模型的精度等级。根据以上数据的计算以及公式(10)和公式(12)，得到上述模型中的C=0.061965026，P=1，参考拟合等级检验评判表可知C≤0.35，P≥0.95，该模型的精度等级为优，平均相对误差经计算结果为1.19%。因此，可以认定本文的GM(1，1)模型可以较为精准地描述该市传染病感染者每日新增人数的变化趋势，也可以用该模型进行未来的传染病感染者每日新增人数的预测，见图1。

通过表3可以发现，全国(除湖北省外)新型冠状病毒感染肺炎的新增人数一直呈现递减的态势，且在2月14-18日新增数持续小于模型预测值，并且差值逐渐增大，说明全国(除湖北省外)居家封闭式管理等措施成果显著，疫情持续向好发展。

利用模型对疫情胜利日进行预测，从图1可以看出，全国(除湖北省外)新型冠状病毒感染的肺炎每日新增人数在4月初趋近于零，即模型预测的疫情“胜利日”为4月初。而实际情况是，除湖北外的全国疫情在3月底(除去境外输入病例)接近结束。

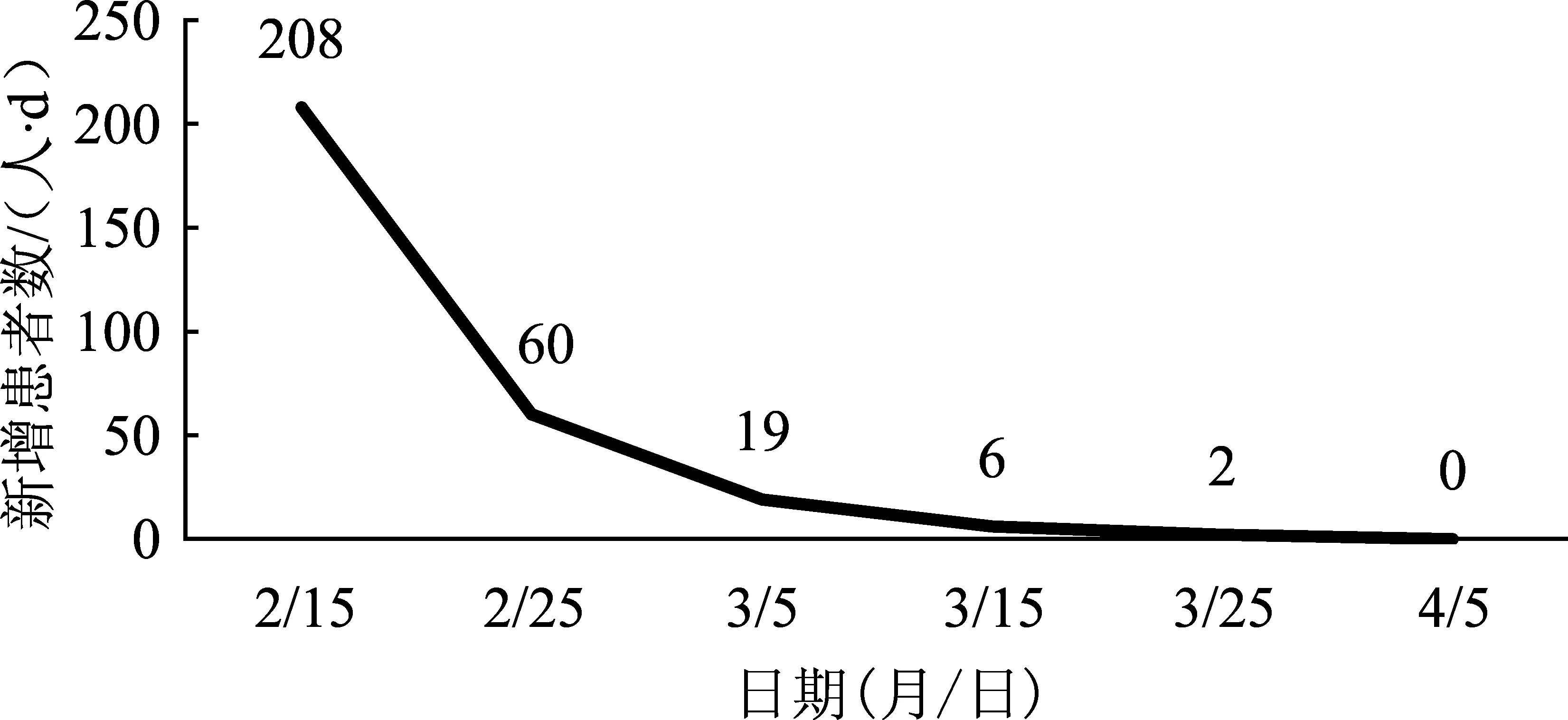
图1 全国(除湖北省外)新型冠状病毒感染的肺炎患者每日新增人数预测

如图2所示，全国(除湖北省外)2月6日到4月2日新型冠状病毒感染的肺炎患者每日新增人数预测值与实际新增人数对比，模型预测时间与实际时间相差不大，说明灰色预测模型在类似传染病等公共卫生事件中，能进行基于历史数据的分析，通过对数据的计算分析出公共卫生事件的大致结束时间。

3 GM(1，1)模型的应用现状

灰色预测GM(1，1)模型的成功应用，解决了生产、生活和科学技术等领域的大量实际问题，应用范围已经扩展到设计、能源、军事、金融、医学、环境、体育等领域。近年来，大量研究者对GM(1，1)算法的优势与局限性进行深入的研究，使其应用于诸多领域。马宁等[6]用灰色模型GM(1，1)预测全国及辽宁省2015-2018年手足口病发病趋势，与实际情况较为符合，模型预测精度为优，能较好的为手足口病防治工作提供参考和科学依据。高凡[7]应用灰色系统理论研究高速列车ATO(列车自动驾驶)系统速度控制器模型，建立的GM(1，1)模型通过实际线路验证了速度控制器的仿真结果，表明该方法具有较高的预测精度，生成的策略能有效地控制列车。康永等[8]利用灰色系统建立GM(1，1)预测模型，将预测结果与实际市场销售量进行对比，发现预测结果与实际市场销售量相吻合，利用灰色预测模型预测销售量，从而减少了制定生产计划中的盲目性，有利于企业的生产调控。

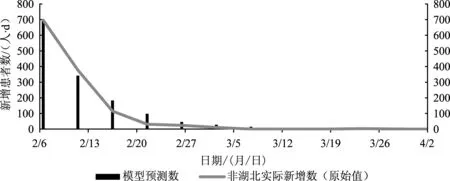
图2 全国(除湖北省外)2月6日-4月2日新型冠状病毒感染的肺炎患者每日新增人数预测与实际新增人数对比

4 结语

自从邓聚龙教授创立灰色系统理论开始，经过20多年的发展，灰色系统理论已成为研究的前沿热点，它涉及多个研究领域，基于“小样本”“贫信息”进行预测的灰色预测方法与其他预测方法相比具有自己的优势。在事件发生初期，信息量有限时，不需要大量数据，只需4、5个统计数据，灰色预测模型就可以预测某特征量随着时间推移变化的规律以及将来的发展趋势。灰色预测模型利用单一的变量建立起来的一阶线性微分动态时间序列模型，可以掌握数据之间的规律，对数据未来的变化规律进行预测[9]。在本文的研究中，基于前期少量的数据建立GM(1，1)模型后利用模型预测疫情的胜利日，与实际日期非常接近，说明灰色预测模型的精确性较好。未来灰色预测模型可以用于医学研究领域，进行疾病发病率、死亡率、新增感染人数等方面的研究分析。