基于Copula函数的导弹部件非线性退化研究*

贺志远，吕卫民，胡文林

(海军航空大学， 山东烟台 264001)

0 引言

导弹部件的许多故障是由于内部材料的性能改变，比如：金属材料的腐蚀，橡胶材料的老化以及电子元器件的失效所导致。研究导弹部件的性能退化过程，合理制定维修决策，对于装备的保障工作具有重要价值。

随着工业制造水平的提高，现代产品的失效机理变得越来越复杂。产品具有复杂内部结构和许多功能，退化过程往往有两个或多个特征参量，并且它们可能是相关的。过去关于退化分析的大多数研究只涉及一个性能特征，当这个关键性能特征参数值降低到失效阈值时，产品失效[1-3]。因此，正确处理各性能退化量之间的相关性，建立多性能退化模型是十分必要的。

目前，在性能多退化模型中，最简单的情况是各特征量线性相关。文献[4]采用主成分分析法，提出了一个PCA-CMAC模型来研究设备的性能退化。对于性能特征之间的复杂相关关系，常用函数来描述性能退化之间的多重相关性。文献[5]采用逆时间尺度变换的逆高斯过程来构建边缘退化过程，通过Copula进行多性能退化建模。文献[6]认为性能退化特性受Winner过程和适应的Copula函数控制，以将特征的退化路径结合在一起。文献[7]建立了具有时间变换的Wiener过程模型评估休眠系统的可靠性，并通过多变量Copula函数描述退化特征的相关性。

某导弹部件具有典型的多性能退化特征，对其退化传统研究方法较为单一。主要存在两个方面的难题：1)该导弹部件属于典型的机电一体化设备，内部包含了电子部分和机械部分，各部分退化规律不同，导致整体退化轨迹呈现非线性。传统的线性退化模型已经无法有效的研究其退化过程。2)退化过程中，往往存在多个具有退化趋势的特征参量，只研究某一退化特征，很可能降低退化分析的准确性。针对以上问题，文中首先建立基于Wiener过程的非线性退化模型，再利用Copula函数进行多性能参数的相关性建模，最后通过实例分析，对导弹部件的退化过程进行研究。

1 基于Wiener过程的性能退化建模

1.1 线性退化

设t时刻产品性能参数的退化量为X(t)，且退化过程可用线性Wiener过程进行表达，则退化模型为：

X(t)=μt+σB(t)

(1)

式中：μ为漂移系数，σ为扩散系数，B(t)为标准布朗运动。

假设该产品的失效阈值为ω，其性能退化轨迹由式(1)的Wiener过程描述，则产品的寿命T可定义为：

T={t:X(t)≥ω|X(0)<ω}

(2)

设μ和σ为固定未知参数，由文献[8]可知，产品寿命T服从逆高斯分布，其概率密度函数为：

(3)

相对应的寿命分布函数为：

(4)

式中：Φ(·)为标准正态分布的分布函数。

1.2 非线性退化

导弹寿命周期任务剖面多变，内部设备的退化机理复杂，退化轨迹也并非全部与时间线性相关，根据这种退化特征，本节建立基于Wiener随机过程的非线性退化模型来描述导弹设备的退化。假设该设备退化过程只有一个关键性能参数，则非线性退化模型表示如下：

(5)

式中：X(0)为初始时刻的性能退化量(为方便研究，令X(0)=0)；μ(t;θ)为非线性函数；σB为扩散系数；B(t)为标准布朗运动，显然，当μ(t;θ)=μ时，式(5)转化为1.1所述的线性Wiener过程。

设σB为固定未知参数，μ(t;θ)是关于t的可导函数，则产品寿命T的概率密度函数为：

(6)

根据文献[9]，设

μ(t;θ)=λbtb-1

(7)

式中：λ为给定的漂移系数；b为固定参数。

将式(7)代入式(6)可得：

(8)

假设模型参数空间不具有随机效应，但不同项在退化中具有可变性，用漂移系数λ表示这种可变性，为了研究随机效应λ，引入以下定理[6]：

引理：若Z～N(μ,σ2)，且A，B，C，ω∈R，则

(9)

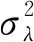
(10)

相应产品寿命T的概率分布函数为：

(11)

可靠度函数可表示为：

R(t)=1-FT(t)

(12)

2 基于Copula函数多性能退化建模

2.1 Copula函数的概念和性质

Copula函数的核心思想[10]可通过Sklar定理实现，若HX，Y(x,y)为联合分布函数，则存在一个Copula函数C(u,v)，对于x,y∈(-,)，满足

HX，Y(x,y)=C(FX(x),FY(y))

(13)

式中：FX(x),FY(y)分别为X和Y的边缘分布。

Copula具有多种构造形式，包括代数方法、几何方法以及Archimedean族[11]生成元构造法。文中主要对比研究Gumbel Copula、Frank Copula、Clayton Copula和Gaussian Copula。

Gumbel:

C(u,v)=exp{-[(-lnu)θ+(-lnv)θ]1/θ}

(14)

式中：θ∈[1,)。当θ→时，u,v→完全相关。

Frank:

(15)

式中：θ∈(-,0)∪(0,+)。当θ>0时，u,v→正相关；当θ<0时，u,v→负相关。

Clayton:

C(u,v)=max[(u-θ+v-θ-1)-1/θ,0]

(16)

式中：θ∈(0,)。当θ→时，u,v→完全相关。

Gaussian:

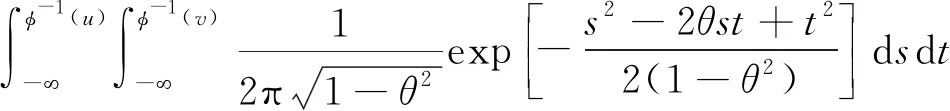
(17)

式中：θ∈(-1,1)。当θ=±1时，u,v完全相关。

2.2 相关性建模

产品有m个性能退化参数，分别为(X1,X2,…,Xm)，分别反映了产品退化过程中的不同特征。本节利用Copula函数对退化过程的不同特征进行相关性建模，为了方便研究，选取具有代表性的二元性能退化参数进行建模分析，并假设它们的退化轨迹符合第1.2节所描述的Wiener随机过程。

设产品退化量X1和X2不互相独立，对应的CDF分别为FT(x1)和FT(x2)，联合分布函数为F(x1,x2)。根据Sklar定理，可得:

F(x1,x2)=C(FT(x1),FT(x2))

(18)

根据Copula函数的性质，联合分布函数的概率密度函数为：

f(x1,x2)=c(FT(x1),FT(x2);α)·fT(x1)·fT(x2)

(19)

式中：c(fT(x1),fT(x2);α)为C(FT(x1),FT(x2))的概率密度函数；α为反映Copula函数中相关性的系数。

为求得相关系数α，由式(19)可得，模型的对数似然函数为：

(20)

式中：γ包含模型中所有未知参数。

3 参数估计

3.1 TSML法

对于1.1节线性退化模型，将式(4)代入式(20)，可得：

(21)

式中：γ=(α,μ1,σ1,μ2,σ2)

对于式(21)，可以直接进行极大化处理，求得未知参数，但由于γ维数较高，求解过程复杂。因此，采用两步极大似然估计法(TSML法)对线性退化模型进行参数估计。主要思路是，先极大化式(20)中不含未知参数α的部分：

(22)

式中：γ1=(μ1,σ1)；γ2=(μ2,σ2)。

根据式(4)，分别对fT(x1)和fT(x2)进行极大似然估计，通过二维搜索法求得相应参数(μ1,σ1)和(μ2,σ2)。再进行第二步似然估计，将相应参数值代回式(20)中求得α的估计值。

3.2 MCMC算法

非线性退化模型复杂，未知参数较多，进行相关性建模后将更加复杂，参数估计时，传统的似然估计法已不再适用。本节采用一种基于贝叶斯理论的Gibbs算法[12]进行参数估计。

设样本γ为一个n维变量，γ=(γ1,γ2,…,γn)，其先验分布为p(γ1,γ2,…,γn)。

Gibbs采样的步骤[13]如下：

当m足够大时，γ(m)可以看作γ的真值，从而求得样本γ的后验分布q(γ1,γ2,…,γn)，进而估计未知参数值。

4 实例分析

以2个月为周期对某导弹进行弹上部件测试，获取多个部件的测试参数，选取光纤陀螺仪作为研究对象。对于光纤陀螺仪主要采集了两个退化特征参量，分别为零偏退化数据和标度因数退化数据，退化数据如图1所示。将零偏退化数据与标度因数退化数据分别记为X1(t)和X2(t)，根据经验及工程实际，将失效阈值设定为ω1=0.5、ω2=1.5。

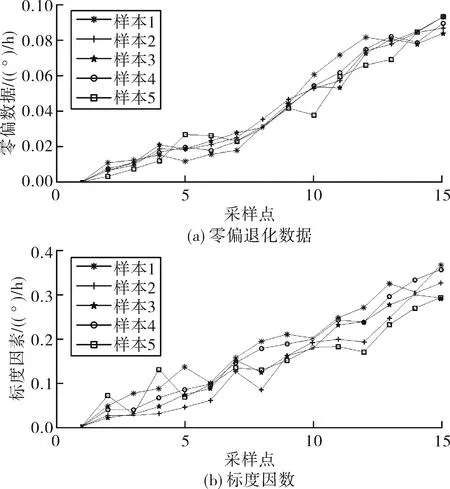
图1 光纤陀螺仪退化数据

首先对数据进行退化建模，分别建立基于Wiener过程的线性退化模型和非线性退化模型；其次，基于Copula函数的线性模型和非线性模型进行相关性建模；最后，对不同模型分别进行参数估计。

由于Copula函数表达形式多样，不同的Copula函数会产生不同的退化概率分布，如果不能选择合适的Copula函数，可能导致结果不正确。因此，对4种不同形式的Copula函数(Gumbel Copula，Frank Copula，Clayton Copula和Gaussian Copula)分别进行建模以及参数估计，通过AIC准则进行检验，为相关性模型选择合适的Copula函数，AIC值越小说明函数拟合效果越好。线性相关模型和非线性相关模型的AIC检验结果如表1所示。

通过AIC检验结果，线性相关模型采用Gumbel Copula函数拟合效果最好，而非线性相关模型采用Gaussian Copula函数拟合效果最好。采用相应的函数，对产品的可靠度进行分析，如图2所示。曲线R1和R4为文中建立的非线性和线性相关模型评估的可靠度；曲线R2为传统的单一性能模型评估的可靠度，选取零偏退化数据作为退化参量；曲线R3为根据光纤陀螺仪真实故障数据评估的可靠度。

表1 两种相关模型的AIC检验结果

图2 不同模型的可靠度曲线

由图2可以看出曲线R1与真实可靠度曲线R3最为接近，证明文中建立的基于Copula函数的非线性退化模型能够更好的描述光纤陀螺仪的退化轨迹。

5 结论

基于Copula函数建立了非线性退化模型，评估了某导弹部件的可靠度，通过与真实故障数据的评估结果对比，证明了模型的合理性。同时，得出以下结论：

1)许多导弹部件的某一性能退化轨迹与时间并非线性相关，传统基于线性随机过程的模型已经无法满足产品的可靠性评估的要求。文中研究的非线性过程能够有效提高评估结果的准确性。

2)多数具有机电一体化特征的导弹部件内部结构复杂，退化过程往往具有多个特征参量，利用Copula函数建立各参量之间的相关性模型，对于导弹部件的可靠性评估具有很好的适用性。

3)文中仅研究了具有退化轨迹的失效模式，实际上还存在其他失效模式，比如，竞争失效。各种失效模式之间的关系值得进一步研究。