黑白棋博弈系统设计

刘佳瑶, 林 涛

(1 河北工业大学 国际教育学院, 天津300131； 2 河北工业大学 人工智能与数据科学学院, 天津300131)

0 引 言

人工智能是近年来非常活跃的研究领域,计算机博弈是人工智能研究的重要分支［1］。 黑白棋在西方和日本是一种深受大众广泛喜爱的游戏,又叫奥赛罗棋(Othello)、苹果棋或正反棋(Anti reversi)。虽然黑白棋规则简单,但其变化复杂,非常有趣味性。 黑白棋程序设计是通过编程使计算机学会黑白棋的规则,使计算机可以与人进行对弈。 本文采用Eclipse 设计博弈黑白棋程序,应用了Minimax 算法进行搜索,通过Alpha-Beta 剪枝减少搜索数量。

1 黑白棋规则

黑白棋由黑、白两种棋子组成,各32 枚,棋盘是64 个8×8 的正方格,棋子要落在方格内［2］。 黑白棋的下棋方法：

(1)在每一场棋局开始时,棋盘的正中间有交叉放置的黑、白棋各两枚,执黑棋一方先落子。

(2)在空的方格新落下己方棋子,同时使对手一枚及以上棋子翻转,为一次合法的落子。

(3)对手棋子被翻转的条件：己方新落下的棋子与棋盘上已有的同色棋子间,被夹住的所有对手棋子(和己方棋子中间无间隙),夹住的方向可以是任何方向。

(4)每次落子可以翻转所有满足条件(3)的对手棋子,可以翻转的对手棋子必须被翻转。

(5)若棋盘上没有位置能实现翻转对方的棋子,则本轮由对手选择落子的位置,直到己方有合法的落子位置为止。

(6)如果一方有合法的落子位置,则必须选择落子,不可以选择放弃。

(7)棋局持续下去,直到棋盘填满或者双方都无合法棋步可下。

(8)当棋盘被下满时,游戏结束；当棋盘上只有一方的棋子时,游戏结束。 游戏结束后,棋盘上剩余棋子多的一方赢得比赛。

2 走棋着法

2.1 局面表达

局面表达指将黑白棋的棋盘上的信息转化为电脑可以识别的数据。 局面表达的过程就是将人机对弈过程中棋局的棋子数据和整体局面信息,用计算机能够识别的语言进行描述的过程［3］。 对于棋子,黑色用B,白色用W；对于黑白棋的棋盘,可以分为横轴和纵轴,横轴用a-h 的英文字母表示,纵轴用1-8 的阿拉伯数字表示。

并做以下定义：

(1)定义棋子的位置Position。 用有两个参数的关键字Position 表示棋子的位置,第一个参数表示棋子的行,第二个参数表示棋子的列(从左到右为0-7,从上到下为0-7)。

(2) 定 义 棋 子 的 颜 色 Player。 用 对 象PlayerWhite 表示白色,用对象PlayerBlack 表示黑色。 类Player 定义玩家棋子颜色,其参数为对象PlayerWhite 或PlayerBlack。

(3)定义棋子Piece。 用两个参数的类Piece 定义一个棋子,第一个参数为关键字Position 表示棋子的位置,第二个参数为类Player 定义玩家棋子颜色。

(4)定义棋盘Board。 Board 列表定义棋盘。 列表元素类型为(3)中的棋子Piece,每次玩家或计算机落子后,将该棋子Piece 类(含颜色和位置信息)加入到列表Board 中。

(5)定义初始棋盘状态initialBoard。 棋盘正中有两枚白棋和两枚黑棋,共四枚棋子交叉放置。

2.2 着法表示

着法指棋子从一个位置挪动到另一个位置,或棋盘上的某个棋子变成其他棋子的过程,着法对应于人机对弈中的行棋［3］。 在黑白棋博弈过程当中着法指：棋盘上所下棋子的位置；人机两方落子后,需改变颜色的棋子；什么情况下游戏结束。

(1)判断落子位置是否为空。 即遍历列表Board 中的每一个元素,判断是否有某一个元素中的位置为落子位置,没有则说明落子位置为空,否则不为空。

(2)将棋子落在该位置,并改变棋盘状态。 首先判断落子位置是否为空,若为空则按2.4 中的方法将可以反转的对手棋子全部反转,否则出现错误。

(3)判断游戏是否结束。 当双方都没有合法棋子可以下时,游戏结束,棋子多的一方获胜,通过Board 的元素个数是否为64 进行判断；当棋盘还没有下满时,如果棋盘上只剩下一个颜色的棋,则游戏结束,棋盘上剩下棋子的一方获胜。 通过判断某一玩家落子并进行相应反转后,Board 中是否仅有一种颜色的棋子进行判断。

2.3 判断本次落子是否有效

黑白棋中落子有效有两个条件：首先要求落子在棋盘的一个空的位置；其次要求新落下的棋子可以翻转对手一个或多个棋子。 因此每次落子前要检查该次落子是否有效,使用isOccupied 函数判断该位置是否为空,使用toFlip 函数判断落子后可以翻转对手的棋子集合是否为空,从而判断本次落子是否有效。

2.4 反转

每次落子后,当自己放下的棋子在所有方向内有一个自己的棋子,则被夹在中间的对方棋子全部翻转成为自己的棋子。 通过穷举实现反转。 落子位置的横向棋子翻转过程如下：

(1)得到棋盘上与所下棋子在同一行的所有棋子的列表row。

(2)从列表row 中筛选出与所下棋子同种颜色的所有棋子,放在列表samePlayer 中。

(3)依次判断所下棋子与samePlayer 中的每一个棋子中间是否全部为异色棋子,是则反转中间的棋子,否则保持不变。

(4)对棋盘上的与所下棋子在同一列、同一条直线上从左上到右下、同一条直线上从右上到左下的棋子,分别进行(1)(2)(3)操作。

3 局面评估

3.1 给不同位置设置权重

对于不同的位置赋予不同的权重w, 使用函数score,计算将己方棋子放在某一位置后,当前棋面上己方的分数s(即当前棋面上己方棋子的个数)。

(1)首先判断是否可以放在四个角落的位置,如图1。 如果可以,则这是最优的位置,令w = 64,保证我方可以尽快占领角的位置。 因为黑白棋的四个角很重要,所以在游戏过程中绝不能轻易的让对手进角［4］。

图1 最优位置Fig. 1 The optimal location

(2)避免在紧靠角的地方放棋子,如图2。 如果放在这个地方,令w = 1。

图2 紧靠角的位置Fig. 2 Right next to the corner

(3)避免在紧靠边的地方放棋子,如图3。 如果放在这个地方,令w = 3。

图3 紧靠边的位置Fig. 3 Close to the side

(4)避免在紧靠边角的地方放棋子,如图4,如果放在这个地方,令w = 2。

图4 紧靠边角的位置Fig. 4 Close to the side and corner

(5)当双方落棋子少于12 枚时(开局系统给出的四枚除外),如果棋子放在蓝色方框以内,如图5所示,令w = s ＋4。 最好不要把棋子放在蓝色方框之外。 这个部分的宗旨是先占满蓝色方框,把对方逼出方框。

(6)早翻转很多对手的棋子实际上会给对手一个优势。 相反,应该采取这样的行动：在棋盘上有一半或更多的棋子之前,尽量将棋子放在可以最少反转对手棋子的位置。 例如：在棋盘上有一半或更多的棋子之前,放在A 位置可以反转对手3 个棋子,放在B 位置可以反转对手5 个棋子,则选择放在A位置。 在棋盘上有一半或更多的棋子之前, 令w =60 - s。

(7)其他情况,令w = s。

图5 中心位置Fig. 5 Center position

3.2 Minimax 搜索

Minimax 搜索算法(即极大-极小算法),该算法要求己方在最坏情况中选择最好的,其第一要义是按照对自己最有利的决策,对盘面进行模拟。 如果能够评价某一时刻其中一方的优劣程度,则另一方走棋时就会选一种使对方优势尽可能小的走法［5］。假设对手每一步都会将我方引入从当前看理论上价值最小的格局方向,即对手具有完美决策能力。 因此我方的策略应该是选择那些对方所能达到的让我方最差情况中最好的,也就是让对方在完美决策下所对我造成的损失最小。

按照这种方式模拟出黑白棋可能的局面,所有局面就构成一棵极大极小决策树,如图6 所示。 第一行为游戏的初始状况,第二行为对手可以下的棋的位置的所有情况,第三行为己方落子可能的情况,以此类推,画出决策树的更深层。 当搜索到预定深度时,对当前局面计算分值估算。 用函数score(Board)算出该层分值,当前层颜色与己方相同时,使之尽可能大。 从而选择己方最坏情况中最好的位置进行落子。

博弈程序消耗的时间与搜索的层数紧密相关［6］。 因此要根据黑白棋的不同难度,以及计算机的运算速度等,设置计算机玩家可以向前看的步数,即决策树的深度。 让计算机又快又准的找到目前最佳位置。

3.3 Alpha-Beta 剪枝

Alpha-Beta 剪枝用于裁剪搜索树中不需要搜索的树枝,以提高运算速度。 基本的原理是：当一个Min 节点的β 值≤任何一个父节点的α 值时,剪掉该节点的所有子节点；当一个Max 节点的α 值≥任何一个父节点的β 值时,剪掉该节点的所有子节点［7］。 本文的黑白棋博弈系统中指的是：删除当前结点获得的值小于其父节点之前得出的值的分支。通过剪枝操作可以有效的减少搜索节点的个数,从而使程序运行更快速。

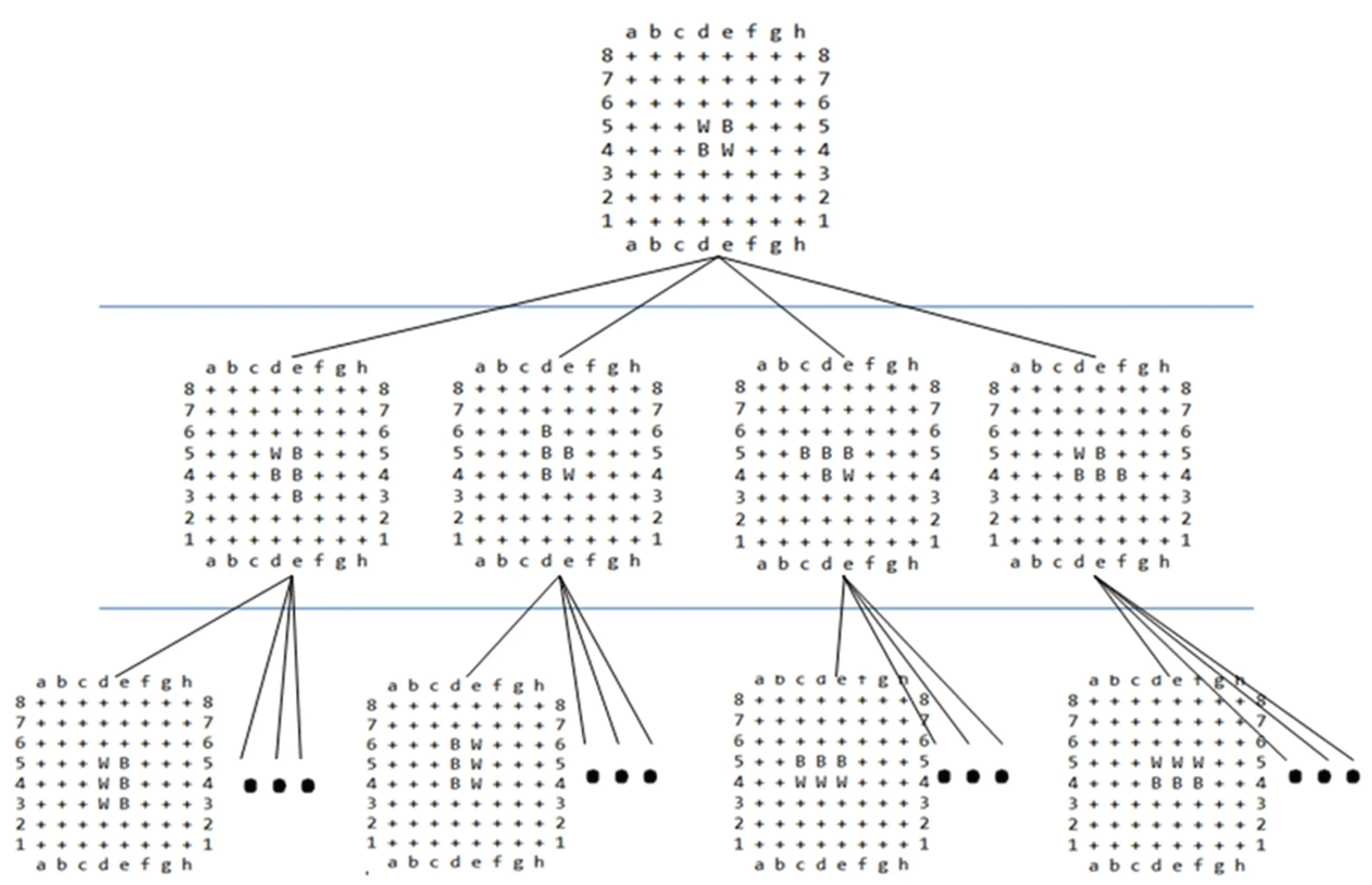
图6 决策树示意图Fig. 6 Decision tree diagram

3.4 其他高级搜索算法

(1)蒙特卡洛树搜索(MCTS)。 蒙特卡洛树搜索算法的最佳下一步的预测完全不同于Minimax 中决策树的生成过程。 MCTS 是对游戏进行多次模拟,最佳下一步的计算是根据尝试和模拟结果进行的。 该方法在保证降低问题规模的同时,能保持所求解的近似最优性［8］。 蒙特卡洛树搜索首先将游戏的当前状态作为一个独立的根节点,例如：在黑白棋中,将当前的棋盘状态作为一个根节点。 然后选择一个节点进行扩展,并模拟,即完成一次从选择节点到博弈结束的过程。 模拟的结果反向传输到根节点,更新根节点信息。 MCTS 算法会在满足最大抽样次数或者达到时间耗尽等设置后,根据第一层节点中每个节点的估值,从中选择一个决策作为本次MCTS 算法的最佳决策［8］。

(2) 遗传算法(Genetic Algorithm)。 遗传算法模拟了生物进化论的自然选择和遗传学机理的生物进化过程［9］。 该算法是通过模拟自然进化过程得到搜索最优解的一种计算模型,且得到演变最后遗留选择的基因,即对应该算法的最优解［10］。 遗传算法在初始化后,要对个体进行适应度计算,在黑白棋中,可根据局面评估中的原则,对棋盘中的位置进行评价。 通过运算将遗传赋给下一代。 当群体的代数达到预先设定值时,适应度最高的个体为最优解,完成算法。 算法运算过程：初始化→个体评价→选择运算→交叉运算→变异运算→终止条件判断。

4 测试与分析

经过人机对弈测试,发现该系统反应较快,计算机出棋时间小于1s。 胜负率上,较为乐观。 测试程序中,一方采用上述算法计算出落棋子位置,另一方模拟真人下棋,随机在可落棋的方格内着棋。 经过100 次测试,该黑白棋博弈系统的胜出次数为87 次。

5 结束语

本文实现了黑白棋的人机对弈系统。 一个较好的人工智能对弈系统来自两个方面的因素：首先是局面评估的准确；其次是博弈搜索的高效性,使程序可以在最短的时间内搜索到足够的深度。 本文在博弈树搜索算法的设计上,运用了Minimax 搜索算法,虽然使用Alpha-Beta 剪枝取得了很好的效果,但是该算法依然会导致游戏树较大,搜索空间较大,需要进一步进行剪枝操作或尝试其他搜索算法。

该黑白棋对弈系统应在以下方面有待改善：(1)局面评估应该更加精准、高效。 (2)在黑白棋下棋的搜索算法中,使用选择性剪枝策略。 (3)尝试使用不同的搜索算法,并进行比较,使黑白棋对弈系统的搜索算法更加快速和精准。