创新能力教学的理论与实践

崔光佐

国际竞争越来越激烈，创新是竞争的核心，培养创新人才已经成为国家的发展战略，培养和提升学生的创新能力是当今教育的核心目标。经由对创新能力进行的系统研究和分析，笔者认为创新能力的核心是发现方法、创建解决方案的心理过程。然后，对创新过程进行了剖析，认为成功解决挑战性问题是培养和提升创新能力的唯一途径。基于上面的结论，对创新能力教学的内涵进行了阐述，并以中小学数学学科为例，对创新能力教学中的问题设计和课堂模式进行了分析和重构。最后，对多年来的中小学数学学科创新能力教学实践进行了小结。

创新能力的核心要素

1.问题的难度

面对一个问题，如果感到困难，原因主要来自两方面：一是缺乏相关知识，对问题相关的对象了解不够;二是无法找到问题的解决办法。我们一般所说的感到困难是指第二个原因。

困难是一种面对问题时的个人感觉，是主观的，每个人的能力水平不同，感觉到的难度就不同。每个人的能力都处在某个水平，当问题的难度高于某人的能力水平时就会感到困难，这个差值越大就会感觉越难，当差值增加到某个值时，就会形成挑战，这样的问题也称为挑战性问题。

2.创新过程

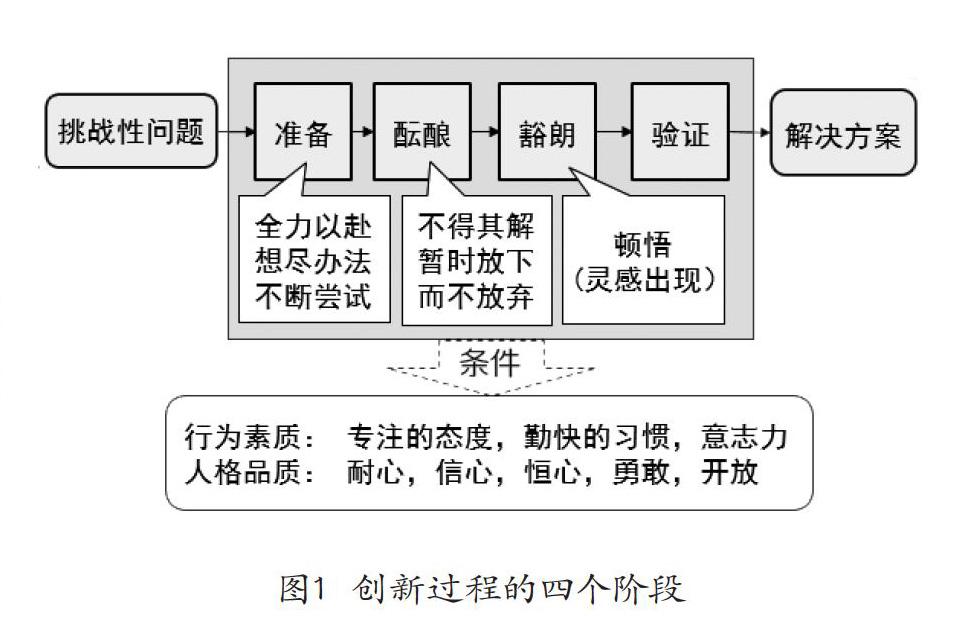
解决挑战性问题的过程是一个发现方法、创建方案的过程，因此是一个创新过程。华莱士将创新过程分为四个阶段，如图1所示。在解决挑战性问题的过程中，起初会不断分析，想尽各种办法，不断尝试探索，但仍然无法找到解决办法，于是不得不暂时放下问题，如果仍然没有放弃，此时便进入酝酿阶段。在酝酿阶段，看起来没有思考问题，但实际上进入了一种称为无意识思考的状态，无意识思考是一种发散性很强的精神活动状态，往往会激活有意识思考状态下无法激活的记忆，更容易产生灵感。研究发现，许多重大科学发现的灵感都是在无意识状态下产生的。

不能发现问题的解决方法，往往是因为对问题相关事物的性質掌握不够，对事物之间的内在联系还没有搞清楚。方法是规律的表现，只有我们发现事物运动变化的规律后，才能找到解决问题的办法。然而，规律是抽象的，隐藏在事物的内部，不能用眼睛直接看到，发现规律需要对事物进行不断地尝试和探索，对表象数据进行归纳抽象，甚至不断猜想和验证。从事物的表象变化数据到发现抽象的规律，是认识的一次飞跃[1]，这种飞跃不是线性过程，不能通过计算得到，而是顿悟过程，需要时间和耐心，是外部事物及其关系在大脑中的抽象加工过程。抽象加工发生在大脑中，常常发生在无意识状态下，具有偶然性，但在头脑中反应的事物越全面，加工的时间越长，顿悟的可能性就越大。对很多科学上重大创新的研究发现，灵感来自于长时间的专注，废寝忘食地沉浸在问题中。

以上的分析表明，创新过程的关键是问题解决者要全力以赴，不断坚持，始终不放弃。要做到这一点至少需要两个方面的心理条件：一方面是专注的态度、勤快的习惯、克服困难的意志力，我们将这些影响行为效率的因素称为行为素质;另一方面是更加稳定的人格品质因素，包括耐心、信心、恒心、勇敢、开放等。我们将这两方面的心理条件称为创新能力的关键因素[2]。

创新能力教学

1.创新能力提升的途径

说明性知识可以用语言传播，通过理解就可以得到。然而，创新能力是一种直接经验，只能通过直接经历成功的创新过程才能得到培养和提升，创新能力提升的模型如图2所示。每个人的创新能力都处在某个水平，当问题的难度高于这个水平时就会感到困难，这个差值越大就会感觉越难;然而，当一个人完全靠自己的努力克服困难，成功解决问题后，这个人的创新能力就会得到提升。

2.创新能力教学

以提升学生创新能力为目标的教学称为创新能力教学，其是提升创新能力的关键因素。基于此，我们可以构建创新能力教学的基本内容。

教学目标：提升学生的行为素质和人格品质等。

教学途径：（1）设计挑战性问题，问题难度要高于学生的能力水平，但不能过高，学生通过一定时间的探索和酝酿可以解决;问题的难度又不能过低，否则学生就不会经历酝酿和顿悟，就不会提升创新能力;（2）学生自主成功解决问题，是指学生要靠自身的努力独立解决问题，亲自经历战胜挑战、克服困难、顿悟发现解决方案的过程，从而提升创新能力。

创新能力教学的问题设计

1.问题设计的基本要求

提升创新能力的唯一途径是成功解决挑战性问题。如何才能成功解决挑战性的问题？可以从四个方面来考虑，第一，从问题内容本身来看，成功解决问题的关键是探索事物本身的固有性质，发现事物内在的必然联系，即发现事物及其变化的规律;第二，从方法上看，发现事物变化规律的基本方法是从多次事物变化的表象数据中归纳出内在的一致性，即变化中的不变性，也就是规律;第三，从心理过程看，发现规律是一个不断探索，不断验证，不断推测，不断归纳，最后通过顿悟发现抽象联系的过程，因此是一个付出高强度努力的辛勤劳动过程;第四，从概率上说，发现事物内在的变化规律是顿悟过程，通过努力和坚持可以增加顿悟的概率，但这种概率不可能是100%，解决挑战性问题存在风险，因此需要勇敢的人格[3]。

以上四个方面是提升创新能力的基本条件，也是创新能力教学中问题设计的基本要求。然而考虑到学生创新能力水平的差异性，要让每位同学都能成功解决挑战性问题，问题设计就要从系统的角度来考虑，按照归纳思维的规律设计由一系列问题组成的问题系统。从我们多年来的经验看，创新能力教学的问题设计可以从以下六个方面来考虑，即问题情境贴近学生的生活，选择学生感兴趣的活动;问题活动基于学生的经验，学生可以动手操作;设计的挑战性问题要紧密结合学科的教学目标;问题对于学生应具有新异性;问题对于学生应具有挑战性，但难度不能过大;问题之间具有内在联系，符合归纳思维的规律。

2.问题设计案例

以人教版小学一年级数学上册的加减法应用为例，设计培养创新能力的系列问题。

学情分析：虽然小学数学一年级上册的知识目标是20以内的加减，但是实际情况是，几乎所有学生都能熟练地数到50，并掌握了50以内的简单加减，但解决应用问题还有难度。

教学目标：利用50以内的简单运算解决鸡兔同笼相关的挑战性问题，培养和提升创新能力，提高素质和人格。

挑战性问题：鸡和兔共有腿34条，兔子比鸡多一只，那么鸡和兔各有多少只？

选择鸡兔同笼问题的理由如下：一年级学生对鸡和兔子较为熟悉;鸡和兔腿数问题有一定的趣味性;可以利用50以内的加减法解决问题;此问题对学生来说是从未见过的，具有新颖性;问题对于一年级学生具有较高的挑战性。

该问题对于一年级的学生具有足够大的挑战，然而要达到创新能力教学的目标，学生必须独立解决问题，亲自经历克服困难发现方法的过程。对于一年级学生来说，几乎还没有解决困难问题的经历，因此，要想让一年级学生成功解决挑战性问题，需要对学生进行适当引导，让学生探索鸡兔同笼问题中隐含的头数和腿数之间的内在联系，最后通过归纳猜想，探索发现问题的解决方案。根据以上的设想，为了让学生独立解决问题，一个有效的引导策略是根据引导目标设计学生能独立解决的问题，因此，问题设计的任务转换为设计由一系列问题组成的问题系统，表1是一年级小学数学加减与鸡兔同笼问题的问题系统设计，其中省略了1-6题知识技能部分，只展示7-16鸡兔同笼相关的十道题，其中的目标一项是指本问题的设计意图。

创新能力教学的课堂模式

从创新过程看，发现解决办法的关键是顿悟，然而顿悟是一个不确定过程，对于难度较大的问题，酝酿阶段往往需要较长的时间，40分钟的课堂时间很难保证学生成功解决问题。因此，创新能力的课堂应该给学生提供若干天冥思苦想的时间，经历顿悟发现的过程，最终成功解决问题，从而提升创新能力。根据我们多年来的实践经验，可以将课堂的思考时间延长到一周，这样每位学生都能够充分尝试顿悟，最后成功解决问题。

创新能力教学实践

十多年来，作者带领北京师范大学研究团队，在全国多个省市开展了从幼儿园到高中的基于数学学科的创新能力教学实践，实际课堂授课超过1500多次，不但提升了实验班学生的创新能力，同时也提升了教师的专业能力和教学水平。尤其是2020年疫情出现以来，团队顺势在校内外展开了完全独立探究的，無讲授的，发现式教学实验。课堂上，教师严格要求，给学生提供一个独立安静的深入思考的环境，学生专注地解决问题，完成的现场提交，未完成的课下继续探究，一周内提交，问题解决的成功率几乎达到100%，学生创新能力提升显著，真正可以做到：让落后的不断进步，优秀的更优秀。

独立解决挑战性问题是提升创新能力的唯一途径，创新能力教学需要特殊的系统化问题设计，经过多年的研究和教学反思，北师大创新能力教学团队对中小学数学的内容进行了广泛的教学实践和案例研究，形成了符合我国中小学数学教学大纲，适合幼儿园到高中的创新能力培养教程，对学生的能力素质提升显著，受到校内外广大用户的好评。

参考文献

马克思，恩格斯. 马克思恩格斯全集（第20卷）[M]. 北京：中共中央马克思恩格斯著作编译局，1986.

林崇德. 教育与发展——创新人才的心理学整合研究[M]. 北京： 北京师范大学出版社，2004.

斯滕伯格. 智力智慧创造力[M]. 王立群译. 北京： 北京理工大学出版社，2007.