天气衍生品定价研究
邹楚瑜


[提要] 天气衍生品是交易资产为标准化的天气指数的金融衍生工具。作为新型的天气风险管理工具,其风险对冲的效果主要由定价模型的预测精度决定。因此,本文使用北京市近60年每日平均气温数据,基于ARIMA模型拟合北京市平均气温动态变化过程,并结合蒙特卡洛模拟法对气温期货进行定价,考察ARIMA模型的预测精度。研究表明:ARIMA模型能够较好地拟合气温动态变化过程,并且以此为基础得到的气温期权价格能够较好地拟合实际价格。
关键词:天气衍生品;ARIMA模型;蒙特卡罗模拟法
基金项目:河北省教育厅重点项目:“农业信贷结构、配置效率与河北省农业经济增长”(编号:SD191051)
中图分类号:F830.91 文献标识码:A
收录日期:2020年7月20日
一、引言
随着全球气候变暖的不断加剧,极端天气发生的频率陡增,灾害破坏力不断加大,各国基础设施、民生和经济发展正在面临日益凸显的威胁。而中国是世界上自然灾害发生最为频繁、灾害种类最多,造成损失最为严重的国家之一,其中干旱、暴雨洪涝、寒潮、台风等灾害对经济社会发展的威胁程度愈发升高,因此对于天气风险的防范工作必须得到广泛关注。相较于上述灾难性天气对经济社会的毁灭性破坏,社会各界对于近年来出现的一般性天气异常现象的重视程度严重不足,例如连续多日高温、雨季提前到来、暖冬等,这些现象对于一国经济的影响不像灾难性天气那样来得迅速、猛烈,但其无异于“温水煮青蛙”,最终可能对一个行业或者整个经济社会产生难以估量的持久不可逆伤害。而我国目前对于上述风险的防控措施十分匮乏,进入21世纪后,天气保险被广泛地运用于灾难性天气的防控和赔偿之中,但这种产品对于应对一般性的天气异常现象几乎没有任何帮助。因此,致力于对冲上述一般性天气风险的天气衍生品逐渐得到政府机构和学术界的重视。
天气衍生品是以气温、降雨量、风力等气象数据计算的天气指数作为交易对象,用以防范宏观、中观和微观经济主体所面临的一般性天气风险的新型金融衍生品。1997年发生的厄尔尼诺暖冬事件促使美国能源企业科赫与安然首次签订天气互换合约,这是天气衍生品迄今为止最早的场外交易记录。1999年,天气衍生品的场外交易规模迅速膨胀,倒逼芝加哥商品交易所(以下简称CME)设计并发现标准化的1月期气温指数期货合约,由此天气衍生品场内交易市场正式建立。随后逐渐推广至欧洲其他发达国家资本市场、日本以及发展中国家之中,交易量迅速攀高。
定价研究是天气衍生品研究的热点。用于天气衍生品定价的模型众多,目前学界关于定价模型达成了一个共识,那就是传统金融衍生工具的无套利定价理论在天气衍生品定价领域不适用,因为天气衍生品的交易资产是不可交易的天气指数,而不是可以实物交割的资产。此外,由于CME市场上流通的产品近90%都以温度指数为交易资产,因此大多数学者的研究主要以温度为标的物的天气衍生品为主,通过各种数理模型来预测气温的动态变动过程并为相应的产品进行定价。天气衍生品的定价模型大致可分为以下两类,即ARMA模型等传统时间序列模型和均值回复模型。传统的时间序列模型的基本实证过程较为相似,大体上是在剔除气温时间序列当中的趋势性因素和季节性因素的基础上,使用ARMA模型等时间序列模型对残差序列进行建模,然后再结合蒙特卡洛模拟法对相应產品定价。学界使用的均值回复模型基于气温的随机变化在长期倾向于回归均值水平的假设,通过不同的气温波动率,如日气温波动率和月气温波动率,结合Alaton(2000)提出的随机微分方程(SDE)来构建模型,最后再依靠蒙特卡罗仿真模拟法对相应产品进行定价。
当前,国内外学界在天气衍生品领域研究的重心不同,国外主要集中于天气衍生品定价问题的探索和改良,而国内大多数学者当前还停留在基础的名片式定性研究当中,研究进展相对落后。因此,本文着眼于天气衍生品定价研究在国内的推广,选择北京市作为研究对象,基于ARIMA模型来拟合北京市的每日平均气温动态变化趋势,并以此为基础结合蒙特卡洛模拟法来对天气期权开展定价研究。
二、数据与研究方法
(一)数据说明。本文选取北京市1960年1月1日至2018年12月31日的日平均气温数据(消除闰年影响后,共计21,535个数据)作为实验组的数据样本,2019年1月1日至2019年12月31日共计365个数据作为测试组的数据样本。全部数据样本均取自中国气象局数据共享网。
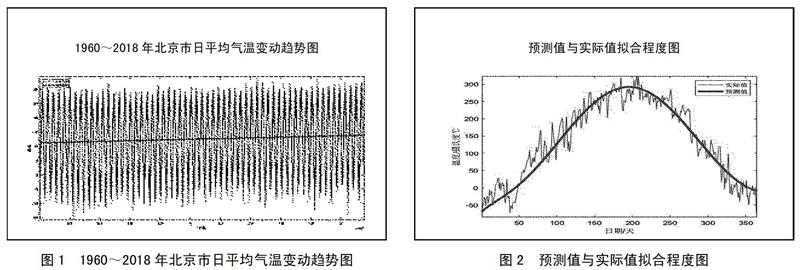
通过绘制气温变动趋势图来直观地呈现气温在区间内的变动情况,如图1所示。可以观察到平均气温存在明显的周期性变化和缓慢的线性递增趋势,这意味着北京市的平均气温在近60年不断的四季更迭中呈现出略微变暖的趋势。(图1)
(二)模型的设定。首先,根据传统的时间序列分析理论将模型的基本形式设定为:
其中,Tt为日平均气温序列,St为气温变动的线性以及季节性趋势变量,而Xt为剔除线性和季节因素后的随机变量(残差)。
从图1不难发现,北京市近年来气温的变动趋势比较接近于正弦函数曲线,此外图1还呈现出略微的线性递增趋势,因此t时刻的趋势变量St可以表示为线性趋势和周期性趋势两部分。具体形式如下:
其中,a+bt为平均气温序列的长期线性递增趋势,βsin(2πft+?渍)为气温序列的周期性变动。β为曲线的振幅,平均气温将在区间[-β,β]内波动;f为曲线的频率,曲线在1/f个时间单位内重复变动趋势,1/f被定义为最小变动周期,本文取f=1/365,此时的最小周期为365天(1年)。?渍为曲线的相位,表示平均气温在时间轴上的任意初始值。
上式可以通过三角函数变换进行进一步简化,如下所示:
由于相位角为常数,可以进一步化简得:
将公式(4)代入公式(1)中,得到平均气温序列Tt的最终表达式如下所示:
三、参数估计与结果分析
(一)ARIMA模型的参数估计。结合公式(5),通过Eviews10.0软件对气温时间序列进行普通最小二乘估计,得到待估参数的估计输出结果如表1所示。(表1)
由表1的输出结果可知,在0.05显著性水平下的各系数值显著大于临界值且拟合优度较高,说明模型拟合效果较好。将参数代入式(5),可得:
从表1还可以观察到DW统计值仅为0.547,查表可知气温时间序列Tt可能存在一阶序列相关,这可能是残差Xt导致的,因此需要对Xt进行修正。将趋势变量St从Tt中剔除后,即可得到残差Xt。通过绘制残差序列图判断出Xt可能不存在显著的序列相关性。通过对残差Xt进行单位根ADF检验,可以判断出在多种信息准则下,一阶差分的残差Xt是一个平稳序列。通过绘制一阶差分的Xt的自相关系数图和偏自相关系数图,可以判断出该序列是平滑的非白噪声序列,因此需要构建ARIMA模型对其进行拟合。根据AIC准则、Schwarz准则和参数的显著性判断,引入ARIMA(2,1,2)模型最为恰当,拟合的具体结果如表2所示。(表2)
从表2中可以看出,各项系数都是显著的,且模型估计的DW统计量为2.002453,十分近似于2。因此,可以初步认为构建ARIMA(2,1,2)模型之后,残差序列中原先存在的相关性问题得到适度的修正。因此,可以得到一阶差分的残差序列Xt和气温时间序列Tt的表达式如下:
(二)模型拟合的精确度检验。根据上式,运用Matlab对2019年北京市日平均气温进行预测,并与2019年实际的平均气温进行比较,得到图2。观察该图能够得出,通过ARIMA(2,1,2)修正后的模型能够较为精准地拟合平均气温的动态变化过程。(图2)
四、天气衍生品定价
(一)天气指数选取。天气衍生品是以天气指标转换而来的指数作为交易资产,其中使用最普遍的天气指数是累积供暖指数(HDDs),被定义为一定时期内的每日平均气温与基线温度之间偏差的累计值。基线温度是一个临界温度,当气温低于该值时,社会各界倾向于开展供暖活动,而当气温高于这一数值时,人们更愿意采取降温措施。不同交易所对基线温度的定义不同,现在最常用的是CME设立的华氏65度(18摄氏度)。HDDs指数的表达式如下:
其中,HDDi是每日的供暖指数,Ti为第i天的平均气温,Tref是基线气温。
(二)基于蒙特卡洛模拟的天气衍生品定价。本文选择基于累积供暖HDDs指数的欧式看涨期权进行定价研究。假设期权为欧式期权(即买方只有在行权日T当天行权的权利),标的指数为HDDs指数,K为合约执行价格,C为价值转换因子(将没有实际货币价值的HDDs指数转化为具体的货币量),U为期权的上限值,r为合约期限内的无风险利率。于是在风险中性条件下,基于HDDs的欧式看涨期权在时刻t的价格如下所示:
其中,HDDs(0,t)是时刻t之前的HDDs数据,是已知量;而HDDs(t,T)是从时刻t到行权日T的HDDs,是需要通过蒙特卡洛模拟来进行仿真的。
结合公式(5)和公式(6),利用蒙特卡洛仿真模拟法进行预测,得到这一期限内基于不同基线温度的累积供暖指数HDDs的期望值,将其和该期限内实际的HDDs指数进行对比得到表3。其中,相对误差率代表真实值相对于预测值的偏离程度。(表3)
从表3中不难看出,在五种基线温度下的相对误差率均小于6%,预测精度较高;另外,随着基线温度的升高,相对误差率递减。
假设北京市2019年2月份的HDDs欧式看涨期权的执行价格K=200(参考现值有利法,设定为低于历年同期水平的价格),合约名义价值C=20,上限值U=10000,无风险利率r=2.72%(取自2019年2月份的一月期SHIBOR利率)。因此,在风险中性条件下,基于不同基线温度的期权价格汇总结果如表4所示。(表4)
从表4中的数据可以发现,在五种基线温度下的相对误差率均小于10%,预测精度较高;另外,随着基线温度的升高,相对误差率递减,且在基线温度为20摄氏度时的相对误差最小,仅为6.85%,这说明将基线温度设定在20摄氏度左右可能更适合于当前我国市场的基本情况。
五、我国天氣衍生品开发及市场发展建议
目前,我国正面临着日益增大的天气风险管理需求与匮乏的天气风险管理工具供给之间的矛盾,诸如天气保险、政策补贴等传统意义上的天气风险管理工具的作用范围和效果有限。而天气衍生产品已经经过了西方资本市场长达二十余年的检验,是一种合格的天气风险管理工具,应该在我国进行适度推广,这不仅需要正确的意识基础,还需要先进的技术支撑和良好的政策环境。
第一,培养正确的天气衍生品风险管理意识。想要推广天气衍生品,当务之急就是让社会各界开始认识、理解并且重视该产品,进而形成正确的天气风险意识,最终培养出数量稳定的市场需求。
第二,进一步发展气象技术、数据分析技术以及金融工程技术。天气衍生品的精准定价要求气象数据尽可能的全面和精准,首先就要求有关气象部门观测、归纳以及共享更为丰富且精准的气象数据;其次需要发明更加先进的数据算法、信息系统等数据分析技术,以便更加高效、准确地处理庞杂的气象数据。不仅如此,还应研究出更为先进的金融工程学理论和实践方法,这样才能将抽象的气象数据转化为社会经济需要的金融产品。
第三,孕育良好的政策和投资环境。天气衍生品在开发、推广和交易中都需要经费支持和政策扶持来抵御较大的不确定性,这就要求政府提供一些切实有效的帮扶政策来分担市场参与者的成本和风险,鼓励更多的机构、企业和个人进入证券市场来转移天气风险,孕育足够具有吸引力的政策环境。同时,市场监管部门应当进行严格的监管和规范,加强对市场准入、信用风险、信息披露以及行业自律的把控力度,必要时可以引入做市商制度来保证天气衍生品发行初期的流动性和价格的合理性,为天气市场的投资者培养出优异的投资环境。
主要参考文献:
[1]刘国光.天气预测与天气衍生产品定价研究[J].预测,2006.25(6).
[2]刘国光,茅宁.气温随机模型与我国气温期权定价研究[J].数理统计与管理,2008.27(6).
[3]李永,夏敏,吴丹.O-U模型在天气衍生品定价中的合理性测度[J].统计与决策,2011.345(21).
[4]郭建国,牛珊.基于ARMA模型的气温衍生品定价研究[J].商业经济,2015.470(10).
[5]曾小艳,陶建平.基于ARMA模型的气温衍生品定价研究:以武汉市为例.区域金融研究,2014.500(7).
[6]Dischel,B.At last:A Model for Weather Risk [J].Energy and Power Risk Management,1998.11(3).
[7]Dornier,F.,Queruel,M.Caution to wind[R].Energy Power Risk Management,Weather Risk Special Report,2000(1).
[8]Alaton,P.,Djehiche,B.,Stillberger,D.On Modelling and Pricing Weather Derivatives[J].Applied Mathematical Finance,2002.9(1).

