一种改进的动态灰色GM(1,1)模型在深基坑形变监测中的预测分析

李豪杰， 独知行， 石 娴， 赵曰耀， 张家威

(山东科技大学测绘科学与工程学院， 青岛 266590)

地铁深基坑的形变监测易受到周边高层建筑、道路及基坑自身荷载的影响，沉降波动较大，传统GM(1,1)模型主要对具有强烈指数规律的单调序列预测效果明显，这给深基坑沉降的后续预测增加了难度，为确保工程安全稳定运行，采用合适的模型改进方法显得尤为重要[1-3]。蒋诗泉等[4]提出应用数值积分思想提高模型参数精度，即通过复化梯形公式对传统GM(1,1)模型背景值进行优化，经算例分析验证了优化后模型对于背景值误差的修正作用；张贵钢等[5]通过权衡信息的时效性，构建了动态GM(1,1)模型，并且通过残差改进，进一步提高了预测值的精度；徐旭等[6]直接从灰色系统理论出发，对非等时距观测值进行变换处理，并在传统模型基础上结合残差GM(1,1)模型，证明了改进方法在高层建筑沉降的可行性。以上模型仅进行了一种或两种方法的改进，且在背景值优化时梯形公式的高次插值会出现Runge现象，得到的预测结果均有待提高。鉴于此，本文以某地铁深基坑工程为例，利用复化Simpson3/8公式优化背景值，同时兼顾新信息的权重和预测残差值，建立了基于背景值优化和残差改进的动态GM(1,1)模型，开展基坑沉降预测研究，取得了良好的实验结果。

1 传统的灰色GM(1,1)模型

1.1 模型构建原理

根据最小二乘原理，解上述微分方程可得：[a,b]T=(BTB)-1BTY,式中：

(1)

则预测值关于时间序列的映射函数即为白化方程的解：

(2)

最后通过累减实现序列还原，预测公式为

(3)

1.2 模型精度评定

为了保证模型预测分析的可靠性，必须对构建的模型进行评价，一般采用后验差检验法[9]。

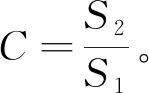
对于评定构建出模型的好坏，主要看C和P，总体来说，C越小越好，P越大越好，具体的精度评定标准如表1所示[10]。

表1 模型精度检验标准

2 改进后的动态GM(1,1)模型

2.1 背景值的优化

灰色GM(1,1)模型预测精度主要取决于参数a、b，而a、b的取值依赖于背景值的构造形式，因此，背景值的构造公式直接影响到模型的预测精度[11]。采用的复化Simpson3/8公式进行优化，即在区间[k,k+1]上选取系列等距分点作为插值节点，利用函数逼近的思想求解背景值。

(4)

B=lnx(0)(k+1)-lnx(0)(k)

(5)

(6)

则称x(1)(t)=AeBt+C，(t≥1)为累加序列的预测模型。

记积分区间[k,k+1]=[a，b]，将区间分成n等份，步长h=(b-a)/n，等距分点tk=a+kh，当n=3时，相应的Simpson3/8插值求积公式如下：

(7)

若将每个子区间[tk,tk+1]划分为3等份，内分节点依次记作tk+1/3、tk+2/3，则复化Simpson 3/8公式即为区间[a,b]内的背景值z(1)(b)：

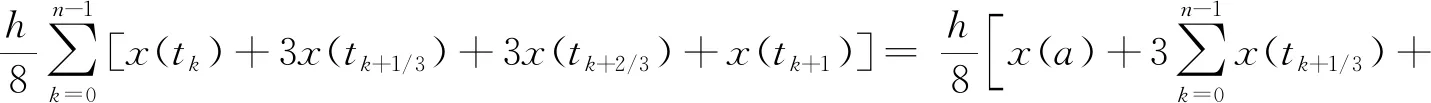
(8)

选定区间划分的份数n后，计算每个子区间的内分节点对应的累加值，再应用式(8)，得到优化后的背景值。相比较传统的算术均值、复化梯形公式，复化Simpson 3/8公式将积分子区间更加细化，对于区域内积分面积的把握更加准确，进而改善了背景值的求积精度。

2.2 动态GM(1,1)模型原理

传统的GM(1,1)模型本质上是指数函数，预测值随时间的增加呈单调递增的变化。在形变监测中，被监测建筑物往往处于一个波动起伏的动态系统中，此时若直接采用传统的GM(1,1)模型进行长期预测，预测值将随时间得增加误差不断增大，精度不断降低[12]。因此需要在预测中加重新信息的权重，即实时引入新的监测信息，淘汰时序相距较远的监测信息，这样改进后的动态 GM(1,1)模型能够比较准确地反映系统的变化状况，从而有效提高形变预测的精度。

利用动态灰色模型进行预测时，要确定好模型的维度，即构建传统模型时的总期数n。首先通过传统的GM(1,1)模型预测得到t=n+1时刻的沉降；再引入实测中t=n+1时刻的沉降x(0)(n+1)，同时去掉原始序列中的x(0)(1)，构建n维动态GM(1,1)模型序列X(0)={x(0)(2),x(0)(3),…,x(0)(n+1)}，得到新的GM(1,1)模型，进而预测t=n+2时刻的沉降值x(0)(n+2)。以此类推，逐个预测，得到实时更新的沉降预测值。

2.3 灰色模型的残差改正

为了达到更好的预测效果，采用n期残差序列作为原始观测数据，构建残差GM(1,1)模型，预测t=n+1时刻的残差值，并结合原来的预测模型进行修正。其改进措施如下：

利用残差原始序列建模：

(9)

联立原模型，构建残差改进后的GM(1,1)模型：

(10)

3 实例分析

该工程主要是对某地铁车站深基坑进行地表沉降监测，在主体基坑施工过程中，围护桩受到自身轴力、桩顶水平位移、桩体水平位移影响，观测数据浮动较大。为了更好预测工程后续的沉降变化，保证车站长期运营和后续维护，从背景值、动态序列、残差值三个方面出发，对模型逐步改进，并将预测值与实测值进行比对分析。现选取沉降观测中较为典型的点位，同时为了确保初始序列呈等时距，选择14期月初的观测数据进行计算分析。利用1～4期沉降观测值构建传统的GM(1,1)模型，得到的时间响应关系式为

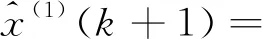
(11)

根据2.1中的定理，通过优化背景值来改进模型求解，优化过程大致为①计算原始序列累加值AGO，将每个区间二等分；②在区间[1,2]内计算累加序列模型x(1)(t)=AeBt+C，并求出各内分节点值；③应用复化Simpson3/8插值求积公式求解改进的背景值z(1)(2)。

以此类推，得出各个区间改进后背景值，构成新的背景值序列Z(1)={z(1)(2),z(1)(3),…,z(1)(n)}。选择前4期沉降数据构建背景值优化GM(1,1)模型，得到优化后的模型关系式为

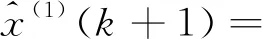
22.878 1

(12)

两种模型的构建结果如表2所示。

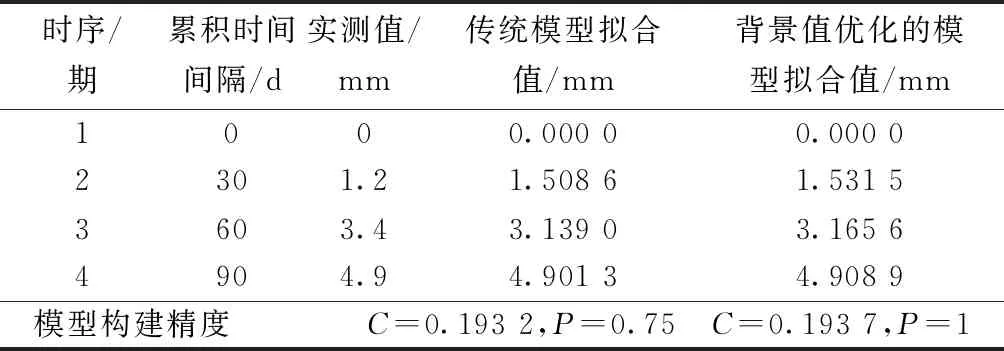
表2 构建传统GM(1,1)模型与背景值优化的GM(1,1)模型

结合表1、表2，选择1-4期观测值构建的传统模型精度为合格，背景值优化的模型精度为优秀。相比于传统模型，背景值优化的模型将构建精度提升两个等级，改善效果明显。由此可见，本文提出的基于复化Simpson3/8公式构建的模型对于波动性较大的数据更具适应性。

根据表2，两种模型均可以进行进一步的预测分析，得到的结果如表3所示。

可见随着时序的增加，实测值离散速度变快，传统模型的预测值与实测值出现较大的偏差，模型整体的预测精度降低。通过优化背景值建立的新预测模型，每一期的相对误差均有改善，但是后期得到的预测值仍不理想，进而考虑在此基础上构建动态优化模型。

通过实时更新观测数据，构建动态GM(1,1)模型，即利用前4期数据建模，预测第5期数据，然后用第5期数据取代第1期数据重新建模，预测第6期数据，以此类推，得到动态预测序列。同时，考虑到残差对预测值的影响，以动态GM(1,1)模型预测值残差为原始序列，构建残差GM(1,1)模型：

(13)

经残差、背景值改进，可以求得动态GM(1,1)模型时间响应函数式为

(14)

代入计算每一期的预测值，分析比较改进后模型的优越性，结果如表4所示。

表3 传统GM(1,1)模型与背景值优化的GM(1,1)模型预测结果

表4 经背景值优化的动态GM(1,1)模型与经残差、背景值改进的动态GM(1,1)模型预测结果

根据表4，经背景值优化的动态GM(1,1)模型的平均相对误差为6.646%，经残差、背景值改进的动态GM(1,1)模型的平均相对误差仅为3.047%。对比表3结果，动态改进后的模型每一期相对误差均明显减小，其中通过残差改进，预测值精度更高，与实测值更为吻合。利用预测值绘制拟合曲线，如图1所示。

图1 传统模型和改进后模型预测值比较Fig.1 Comparison of traditional models and improved model predictions

由图1可以看出，观测期间原始数据的波动起伏较大。从第10期观测开始，观测值逐渐趋于稳定，传统GM(1,1)模型和背景值优化的GM(1,1)模型仍保持单调上升的趋势，与实测值差距越来越大。基于残差、背景值优化的动态GM(1,1)模型始终随着观测数据的变化而变化，且二者的数值十分接近。

4 结论

在传统GM(1,1)模型基础上，利用复化Simpson3/8公式优化背景值，进而改善了模型的整体精度，这在模型构建中体现较为明显，但随着期数的增加，预测值与实测值间出现较大的偏差。通过构建背景值优化的动态GM(1,1)模型，可将预测精度提高23.405%，预测值与实测值趋势更加吻合。考虑到在新旧信息迭代过程中不可避免会累积一些观测值偶然误差，为此进行的残差改进可将模型预测精度再次提高3.239%。因此，基于背景值优化、残差改进的动态GM(1,1)模型精度更高，更具适用性，继而可以作为该工程的预测模型来进行后续的研究分析。