基于问题表征的物理学科核心素养研究*

张贵洲

(徐州市铜山区茅村中学 江苏 徐州 221135)

高中物理课程作为普通高中课程的重要组成部分，目的是进一步提升学生的物理学科核心素养．物理学科的核心素养是学生在学习物理的过程中，通过发现问题、提出问题、分析问题、解决问题所形成的物理观念、科学思维、科学探究和科学态度与责任．

教师通过物理教学，引导学生形成物理观念，并利用物理观念进行解释现象和解决问题．物理观念的教学流程通常为：首先教师提出一个问题，引导学生对问题进行分析讨论，接着通过探究得到问题的结论，即通过对物理问题的解决帮助学生形成物理观念．科学推理和科学论证既是科学思维的重要组成部分，也是探究发现式教学的重要组成部分．因此教师通常采用探究发现式的教学流程，引导学生通过对问题的解决提升学生的科学思维素养．科学思维素养还包括模型建构，新课标中要求高中阶段学生能够将实际问题或较复杂问题中的对象和过程转换成物理模型．在日常学习中学生借助所学物理概念、物理规律解决物理问题时，需要从题干提取相应信息建立对应的时空关系，进而将物理问题纳入特定的物理模型以此将问题解决[1]．

鉴于以上分析，物理学科核心素养的形成建立在物理学科的学习过程之中；物理学科的学习过程主要是对物理问题的解决过程，而问题表征是贯穿于整个问题解决过程中的一个动态过程，从问题的呈现至问题的解决都有各种表征形式和表征状态的存在．在问题解决过程中，问题解决者从问题的外部特征开始，逐步而深入理解问题的深层结构，从而达到对问题的解决，进而提升学生的学科核心素养．

廖伯琴博士在基于McDermott&Larking表征分类假设的基础之上，提出问题解决者在解决物理问题的过程中需要依次经历文字表征、朴素表征、物理表征和数学表征[2]．根据对问题表征的层次分析，笔者选择所在学校低年级和高年级的学生对其进行施测，采用认知作业分析法借助SPSS22.0对其在解决物理问题过程中的表征差异性进行研究，以此提出提升学生物理学科核心素养的建议．

研究中选取以下物理问题对学生进行施测：

物理问题：游乐场近期推出一系列体验项目，其中一项如图1所示，60 kg参赛选手以初速度v0=7 m/s的水平速度借助悬挂在高处长L=6 m的绳子飞越到对面的高台上．当绳摆到与竖直方向夹角θ=37°时，选手放开绳子后恰好运动到最高点A，长xAB=3.75 m传送带始终以v1=3 m/s的速度匀速逆时针运动．选手与传送带的动摩擦因数为0.2，不考虑空气阻力和绳子的质量．(其中选手可视为质点，取重力加速度g=10 m/s2,sin37°=0.6,cos37°=0.8)求：试通过计算说明该选手是否能顺利冲过终点B．

图1 选手运动过程示意图

解析：

第一阶段，由水平位置开始的圆周运动，由机械能守恒定律得

(1)

H=L-h=L-Lcosθ=1.2 m

(2)

由式(1)、(2)联立可得

v=5 m/s

第二阶段，由松手处至A点的逆向类平抛运动，选手在放开绳子时，水平速度为vx，竖直速度为vy则

vx=vcosθ=4 m/s

(3)

vy=vsinθ=3 m/s

(4)

由于恰好到达最高点A，则此时vy=0，vx保持不变．

第三阶段，由于选手运动方向与传送带运行方向相反，所以在传送带上做匀减速直线运动.

选手的加速度大小

(5)

以地面为参考系，选手在最高点A有向右的初速度vx，向右运动的最大位移为末速度为零时的位移

(6)

联立式(3)、(5)、(6)可得

x=4 m>3.75 m

所以可以顺利通过终点．

问题表征的层次界点及评分标准如表1所示.

表1 表征层次界定及评分标准

信效度检验：本研究采用SPSS 22.0进行问卷的信效度检验．从表2中可以看出，Cronbach′s Alpha值为0.870，量表的总体一致性较高，信度较好．此外，本量表借鉴了以往文献关于该问题的量表研究，在内容效度和结构效度上更符合高中生学习的实际情况；一般认为，量表的难度系数在0.3～0.7之间较为适宜，本量表的难度系数为0.61，因此，本量表的整体信效度较好．

表2 观察值处理摘要&可靠性统计资料

研究结论：通过对不同年级学生的认知作业进行整理与分析，从中可以发现,高年级学生和低年级学生的认知作业大多数依次经历了文字表征、朴素表征、物理表征和数学表征4个层次．现从问题表征的表征层次进行分析如下.

(1)对于物理问题文字表征情况，我们通过SPSS进行差异性分析后得出表3和表4.

表3 物理问题的文字表征Crosstab

表4 物理问题的文字表征Chi-Square Tests

卡方检验方法：由样本量的大小来决定参考表中数值，如总样本数N>40且交叉表中每一个cells中频数均大于5，检验的结果是精确的，可参考第一行指标pearson-chi-square，若sig值小于0.05，说明差异显著；如样本总量N<40或cells中有一频数小于5，则取校正后的卡方值，即第二行数据或者第三行fisher精确概率法获得值．

由以上两表可知，低年级学生与高年级学生错误发生的频次皆较少，Pearson Chi-Square中Asymp.值为0.712>0.05，说明在文字表征层次上，低年级学生和高年级学生表征差异不明显，表征水平接近．

原因分析：物理问题的文字表征是对题目内容进行一些表面的理解，考虑到高中阶段学生所具有的文化素养极易达到，因此，学生对问题中文字描述的理解已经达到了较高的水准．部分学生出现文字表征错误主要是由于其学习态度较差，自我效能感较差．

素养提升：物理学科核心素养要求学生具备科学态度与责任，要通过物理教学使学生养成严谨认真、持之以恒的学习、工作态度．因此在重视学生知识获取的同时，也要培养学生学习物理的兴趣，学生接受物理、热爱物理，自然不会出现空白卷的情况．同时，学生利用物理知识解决物理问题的过程也能让学生体会到物理知识是有用的，进而产生学习物理的兴趣和情感．

(2)对于物理问题朴素表征情况，我们通过SPSS进行差异性分析后得出表5和表6.

表5 复杂物理问题的朴素表征Crosstab

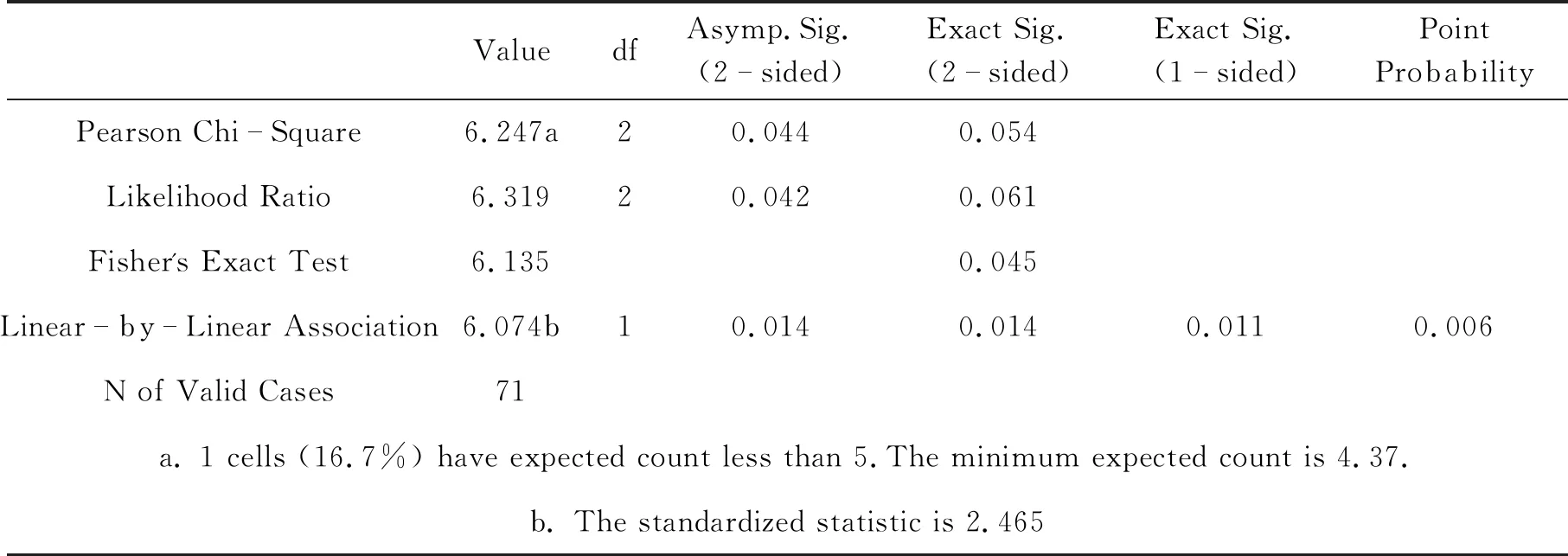
表6 物理问题的朴素表征Chi-Square Tests

由以上两表可知，根据低年级学生与高年级学生错误发生的频次和Pearson Chi-Square中Asymp.值为0.044<0.05，说明在朴素表征层次上，低年级学生与高年级学生存在显著性差异．

原因分析：要解答物理问题就需要正确地对选手不同运动阶段进行表征，题目中存在的冗余信息以及信息中潜在的歧义性会使被试在解答问题中产生错误的解题思路，导致错误解题．例如，低年级学生发生以下错误，选手运动过程表征错误，选手在传送带上最大运动位移判断错误，运动过程图像描述发生错误．

素养提升：学生不能建立正确的时空关系，即朴素表征错误，直接影响学生将实际问题中的对象和过程转换成物理模型，进而物理问题得不到解决．学生模型建构素养的提升是建立在正确的朴素表征之上的．分析学生朴素表征中的错误，教学中应引导学生结合个体生活经验理解基础知识，提升学生朴素表征程度进而提升学生的模型建构素养．

(3)对于物理问题物理表征情况，我们通过SPSS进行差异性分析后得出表7和表8.

表7 物理问题的物理表征Crosstab

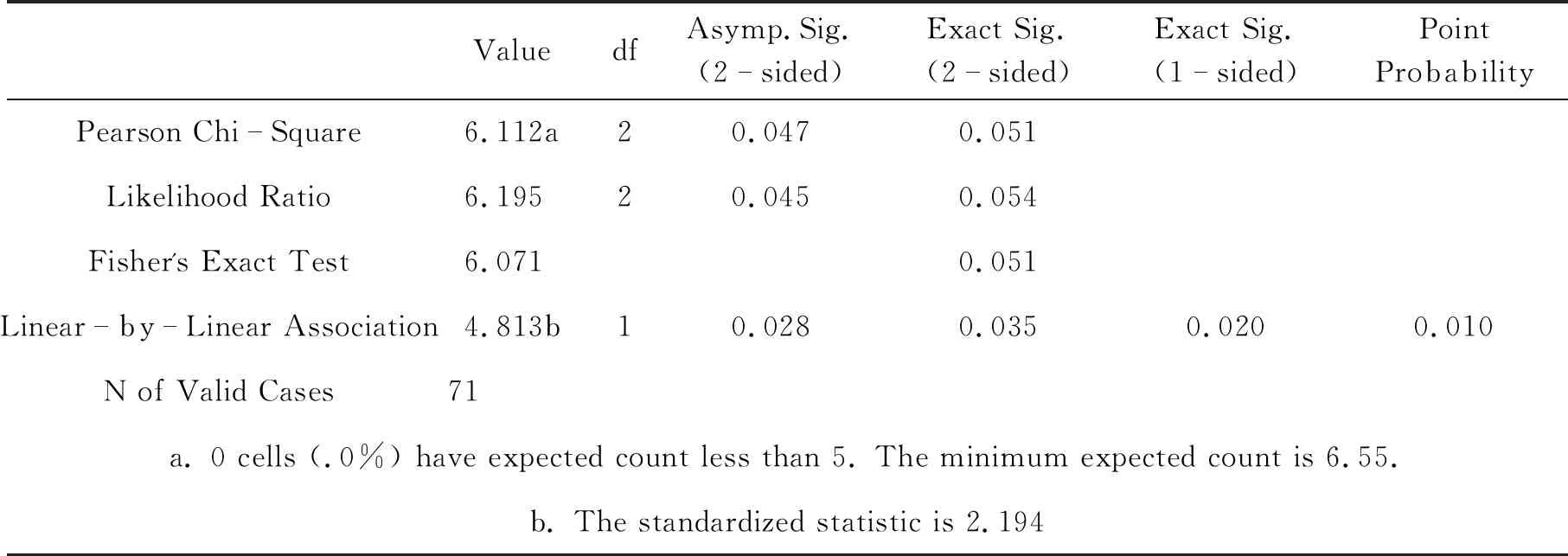
表8 物理问题的物理表征Chi-Square Tests

由以上两表可知，低年级学生错误发生的频次明显高于高年级学生错误发生的频次，Pearson Chi-Square中Asymp.值为0.047<0.05，说明在物理表征层次上，低年级学生和高年级学生存在显著性差异．

原因分析：高年级学生拥有更大更多的包含有关领域陈述性知识的问题图式，且图式中的知识被良好组织，知识单元间高度连接．相较而言，低年级学生拥有的陈述性知识图式是不完善的，包含较少相关领域，图式中知识组织、知识间链接松散．导致低年级学生错误主要表现在错误提取物理公式，物理公式中所使用符合与题目不相符，计算过程中没有注意单位的使用．

素养提升：学生的问题图式主要包括理想化的物理模型、物理概念及规律，能否正确进行物理表征取决于学生对物理概念或原理的理解．因此，帮助学生建构结构优化的高中物理知识系统和在教学中学习更多的物理概念及规律能够提升学生的物理观念和科学思维素养．

(4)对于物理问题数学表征情况，我们通过SPSS进行差异性分析后得出表9和表10.

表9 物理问题的数学表征Crosstab

表10 物理问题的数学表征Chi-Square Tests

由以上两表可知，低年级学生与高年级学生错误发生的频次皆较多，Pearson Chi-Square中Asymp.值为0.336>0.05，说明在数学表征层次上，低年级学生与高年级学生在解决物理问题的过程中差异性不明显．

原因分析：高中物理问题对学生的数学运算能力的要求低于同期数学学科核心素养的要求，因此大部分学生能进行完全表征．

素养提升：学生数学学科核心素养影响物理问题解决的数学表征，学生数学表征错误表现为，错误提取数学三角函数式，计算数据出现错误．纠正学生日常学习中的错误，提升学生数学素养，达到对物理问题的完全表征．