基于拟合改进的径流灰色预测模型研究

武桂芝 王程

摘 要：经典灰色模型可用于水文径流预测，但其预测精度较差。为了提高模型精度，基于经典灰色理论，对累加后的数据进行精度更高的多项式拟合，建立基于拟合改进的径流灰色预测模型。该模型简单易行，且计算精度和效率较高。通过对三门峡水库的入库径流资料进行经典和拟合改进灰色预测，表明拟合改进灰色预测模型可有效地对径流进行预测，预测精度较经典灰色模型有较大提高。

关键词：径流预测;灰色预测模型;拟合改进;三门峡水库

中图分类号：P338;O159;TV882.1 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.10.007

Research on Runoff Grey Prediction Based of Improved Fitting

WU Guizhi1， WANG Cheng2

（1.Henan Vocational College of Water Conservancy and Environment， Zhengzhou 450008， China;

2.Information Center， Henan Yellow River Bureau， Zhengzhou 450004， China）

Abstract：Classical grey model can be used into hydrologic runoff prediction， but has bad prediction accuracy. Based on the classical grey theory， this paper utilized polynomial fitting to higher precision fit cumulative data and built improved runoff grey prediction model. This model could be easily used and realized by program， and also had high calculation accuracy and efficiency. By predicting inflow runoff of Sanmenxia Reservoir through classical and improved grey prediction， it shows that the latter method can effectively predict runoff and has improved calculation accuracy.

Key words： runoff prediction; grey prediction model; improved fitting; Sanmenxia Reservoir

1 引 言

径流预测是指根据前期或现时已出现的水文、气象等信息对径流进行定量或定性预报，是水利水电工程設计、施工和运行管理的重要依据，如何对径流进行精确预测是水利工程设计与运行的关键问题之一[1]。

目前针对径流预测已有统计预测法[2]、人工神经网络预测法[3-4]及机理模型预测法[5-6]等多种预测方法。灰色系统模型是统计预测法中应用较广泛的，由于灰色系统模型不需要大的统计样本和数据的规律性分布，且模型简单易行，因此在径流预测中得到广泛应用[7-8]。灰色系统有多个预测模型，其中常用的是灰色系统经典模型，即GM（1，1）模型。灰色系统经典模型适用于累加（累减）后呈指数平滑分布的数据序列，如果累加（累减）后的数据分布与指数分布吻合度较差，那么灰色系统经典模型的适用性就会减弱。径流资料不确定性强、统计规律较差，导致灰色系统经典模型在进行径流预测时容易出现较大误差。

笔者针对灰色理论指数拟合的精度问题，提出精度更高的多项式拟合，该计算模型仅对累加后数据进行高次拟合，精度较经典灰色模型有所提升。

2 基于拟合改进的灰色理论预测模型

灰色系统理论是通过对系统某一相关方面的观测数据加以数学处理，从而达到了解系统内部总体变化趋势、相互关系的一种理论。“灰色”是相对于“黑色”和“白色”而言的，“黑色”表示信息缺乏，“白色”表示信息完整，而“灰色”则表示信息不完整、不完备。

灰色系统建模的基本思想是对无规则的原始数据进行处理（累加或累减），生成可寻找出内在规律的数据序列，进而再进行建模预测。将时间序列转化为微分方程，从而建立抽象系统发展的动态变化模型，可对系统的发展作出相关预测。灰色系统预测具有准确性好、需要原始数据少、数据处理简单、可靠性高等特点，已在多个领域得到广泛应用。

灰色系统经典模型GM（1，1）是一个近似指数型发散的预测模型，由一个一阶方程和一个预测变量模型组成，适用于累加（累减）序列近似服从指数分布规律的系统。其模型建立与预测规则如下。

（1）设长度为n的原始数据序列为

X（0）=（x（0）（1），x（0）（2），…，x（0）（n））（1）

式中：x（0）（n）为数据序列中的第n项。

（2）判断建模的可行性，进行级比检验：

σ（k）=X（0）（k-1）X（0）（k） （k=1，2，…，n）（2）

式中：σ（k）为原始数据序列X（0）的第k-1项与第k项的比值。

若-2en+1≤σ（k）≤2en+1，则该序列可采用GM（1，1）建模并进行预测。

（3）对数据序列X（0）进行累加处理，得新序列X（1）。

X（1）=（x（1）（1），x（1）（2），…，x（1）（n））（3）

其中x（1）（i）=∑ik=1x（0）（k）。

式中：序列X（1）为对原始数据序列X（0）作一次累加得到的新序列。

（4）由序列X（1）可建立一阶微分方程

dx（1）dt+ax（1）=b（4）

式中：a、b均为待定参数，其中a为发展系数，b为灰作用量。

（5）令Z（1）=（z（1）（2），…，z（1）（n）），其中z（1）（i）=0.5[x（1）（i）+x（1）（i-1）]。参数列可表示为

P1=（BTB）-1BTYTn=[a，b]T（5）

BT=-z（1）（2）-z（1）（3）…-z（1）（n）11…1（6）

YTn=[x（0）（2），x（0）（3），…，x（0）（n）]（7）

式中：BT为2×n的矩阵，YT为1×n的矩阵。

（6）采用最小二乘法计算发展系数：

Y（1）（k+1）=[X（0）（1）-ba]e-ak+ba（8）

因Y（1）（k+1）是通过累加计算得出的，故需还原数据得到预测的实际值，即

Y（0）（k+1）=Y（1）（k+1）-Y（1）（k） （k=1，2，…，n）（9）

式中：Y（0）（k+1）为原始数据序列的第k+1项;序列Y（1）（k+1）、Y（1）（k）分别为对原始数据序列Y（0）作一次累加，得到新序列Y（1）中的第k+1、k项。

笔者提出的灰色系统改进模型引入拟合多项式作为累加（累减）后的“微分方程式”，通过拟合后的多项式建立数据统计规律，对新序列进行预测分析，将累加（累减）后得到的值作为改进模型的灰色预测值。该模型对数据的适应性强，可针对数据进行高精度的数据拟合，从而得到较为精确的预测值。对式（9）进行多项式拟合，生成了新序列Y（1）。

Y（1）（i）=a0+a1i1+…+akik+…+amim （i=1，2，…，n） （10）

式中：ak为拟合多项式的系数;m为多项式的最高次幂。

由于新序列Y（1）是对X（1）序列进行预测得到的，因此对Y（1）进行累减可生成预测实际值Y（0）。

Y（0）（i+1）=Y（1）（i+1）-Y（1）（i） （i=1，2，…，n）（11）

式中：Y（0）（i+1）为原始序列的第i+1项;序列Y（1）（i+1）、Y（1）（i）分别为对原始序列Y（0）作一次累加后得到新序列Y（1）的第i+1、i项。

改进灰色理论预测模型不改变灰色系统经典模型内部的运行机理及其适用范围，仅对累加后数据进行更高精度拟合，在不影响计算效率的基础上，预测精度有较大提高。

3 实例分析

3.1 实例选择

选择三门峡水库对本研究构建的径流预测系统进行验证。三门峡水库是黄河上的第一座大型水利枢纽工程，1957年正式投入使用，是治黄工程体系最重要的组成部分，担负着黄河下游防洪、防凌的重任。

3.2 入库径流分析

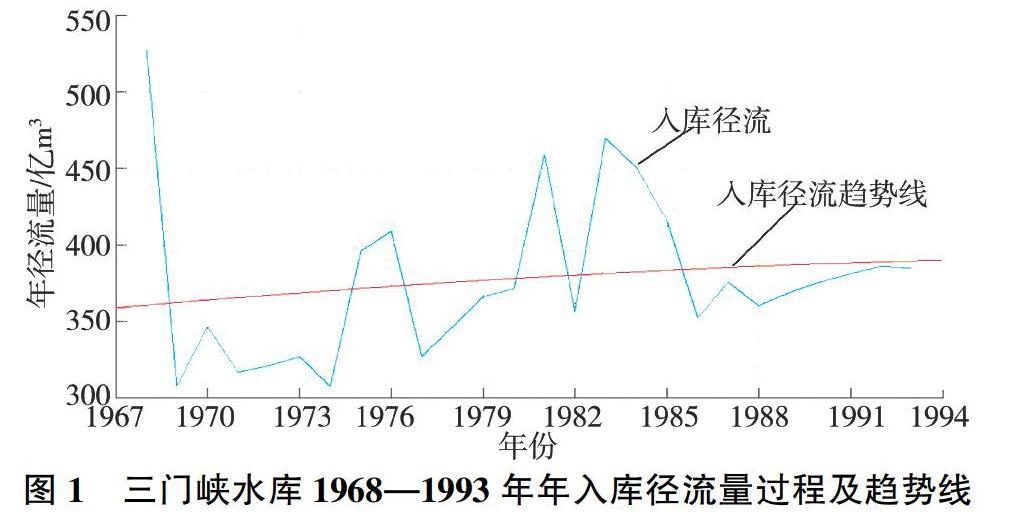
采用参考文献[7]中三门峡水库1968—1993年共26 a的入库径流量作为分析数据，年径流量变化过程及其趋势线如图1所示。水库多年平均入库径流量为376.94亿m3，其中最大径流过程发生在1968年，为527.2亿m3，最小径流过程发生在1974年，为307.4亿m3。

为对入库径流过程进行水文分析，将多年径流量序列按年径流量从大到小进行排频，并采用P-Ⅲ型曲线进行拟合，拟合成果如图2所示。

根据年径流量P-Ⅲ型曲线拟合结果，分别选择对应频率P=5%、25%、50%、75%、95%的年份作为特丰年、丰水年、平水年、枯水年、特枯年，并在三门峡实际入库径流过程中选择对应的典型年进行分析，其对应关系见表1。

对丰水年、平水年和枯水年的设计年径流量与水库实际的多年径流过程进行比较，如图3所示。

通过对表1及图3的分析可知，本研究选择的三门峡水库的入库径流过程包括特丰年（5%频率）、丰水年（25%频率）、平水年（50%頻率）、枯水年（75%频率）和特枯年（95%频率），水文径流过程具有一定的代表性。

3.3 径流预测分析

以1968—1988年作为原始数据年份，以1989—1993年作为预测径流年份，并对1989—1993年的预测年径流量与实测年径流过程进行对比分析。

对选取的1968—1988年的年径流资料进行累加生成新的序列，分别对其进行经典灰色理论指数拟合和改进灰色理论多项式拟合，拟合结果的相对误差如图4所示。可以看出，改进灰色理论拟合的相对误差较经典灰色理论有所减小，经典灰色理论拟合相对误差平均值为1.48%，而改进灰色理论拟合相对误差平均值仅为0.93%。

利用经典灰色预测模型和改进灰色预测模型对三门峡水库1989—1993年的年径流过程进行预测，并与实际径流过程进行对比，见图5和表2。

由图5及表2可知，经典灰色理论模型和改进灰色理论模型均可以对径流过程进行预测，且预测结果与实测径流过程的趋势均吻合。经典灰色理论拟合预测数据呈直线上升，与实测径流量吻合较差，而改进灰色理论预测数据呈二次曲线分布，且变化规律与实测径流量较为吻合，原因是改进灰色理论预测模型对累加数据进行了误差更小的多项式拟合，消除了累加数据的拟合误差。

由表2可知，经典灰色理论模型的预测相对误差平均值为13.15%，最大预测相对误差为14.37%，最小预测相对误差为12.55%;改进的灰色理论模型的预测相对误差平均值仅为5.07%，最大预测相对误差为9.60%，最小预测相对误差为1.61%，预测精度有较大幅度提高。可见，在采用灰色预测模型进行径流预测时，可以采用本研究提出的预测精度更高的改进灰色预测模型进行预测。

4 结 语

改进灰色理论预测模型不改变灰色系统经典模型内部的运行机理及其适用范围，仅对累加后数据进行更高精度拟合，改进后的模型在三门峡入库径流预测中的应用表明，在不影响计算效率的基础上，其预测精度有较大提高。

参考文献：

[1] 李红波，夏潮军，王淑英.中长期径流预报研究进展及发展趋势[J].人民黄河，2012，34（8）：36-40.

[2] 李颖慧.基于灰色系统模型的三峡库区水污染预测与治理对策研究[J].重庆理工大学学报（社会科学），2020，34（3）：46-55.

[3] 徐中民，蓝永超，程国栋.人工神经网络方法在径流预报中的应用[J].冰川冻土，2000，22（4）：372-375.

[4] NAEHIMUTHU K， WILLIAM J G， MEMBER， et al. Neural Network for River Flow Prediction [J]. Journal of Computing in Civil Engineering， 1994，8（2）：201-220.

[5] LAURA M， JON H， MICHAEL B， et al. Adapting the Relaxed Tanks-In-Series Model for Storm Water Wetland Water Quality Performance[J]. Water，2017，9（9）：691.

[6] XIA M， JIANG L. Application of an Unstructured Grid-Based Water Quality Model to Chesapeake Bay and Its Adjacent Coastal Ocean[J]. Journal of Marine Science and Engineering， 2016，4（3）：52-60.

[7] 藍永超，杨志怀，权建民，等.灰色预测模型在径流长期预报中的应用[J].中国沙漠，1997，17（1）：49-52.

[8] 赵璀.灰色系统在瑞丽江长期水文预报中的应用[J].云南水力发电，2007，23（6）：5-7.

[9] 马建琴，许龙宾，师琨.改进型灰色马尔科夫模型在径流预测中的应用[J].华北水利水电学院学报，2012，33（2）：39-42.

【责任编辑 张 帅】