小浪底水库泄水孔洞调度方案比选研究

江颖 李珍 安静泊

摘 要：小浪底水利枢纽进水塔群前的泥沙淤积影响工程的安全运行和水库的发电效益，制定合理的泄水孔洞调度方案至关重要。为此采用立面二维水沙数学模型开展小浪底水库底孔防淤堵的数值模拟研究。在设计水沙条件下，计算和比较两种泄水孔洞运用方案对坝区河床纵剖面淤积形态、排沙比和发电效益的影响，结果表明：两种方案均能满足进水塔群防淤堵的要求，为尽可能发挥小浪底水库的发电效益，泄水孔洞调度方案推荐方案1，即出库流量小于发电洞泄流量时优先启用发电洞泄流，当出库流量超过发电洞泄流量时超出部分尽量通过排沙洞、明流洞、孔板洞泄流，减少库区淤积。

关键词：小浪底水库;防泥沙淤堵;立面二维水沙数学模型;泄水孔洞调度方案

中图分类号：TV697.1;TV882.1 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.10.003

Comparison of Operation Dispatch Scheme of the Discharge Outlets in the Xiaolangdi Reservoir

JIANG Ying， LI Zhen， AN Jingbo

（Xiaolangdi Multi-Purpose Dam Project Management Center， Ministry of Water Resources， Zhengzhou 450000， China）

Abstract：Preventing sediment siltation in front of intake tower group of the Xiaolangdi Reservoir affects the safety operation and the generation benefits of the project. It is vital to determine a proper operation dispatch scheme of the outlet structures. This paper did the numerical research on the prevention of silt plug in the Xiaolangdi Reservoir by a vertical 2D numerical model. The bed evolution， sediment delivery ratio and generation benefit were discussed under typical water and sediment conditions with the two different dispatch schemes of the outlets. The results of the numerical modeling show that neither of the dispatch schemes will cause the sediment siltation and the scheme 1 shows a better performance in promoting the generation benefits. The present work provides the technical support for the operation dispatch scheme of outlets in engineering practices.

Key words： Xiaolangdi Reservoir; preventing sediment siltation; vertical 2D numerical model; operation dispatch scheme of outlet structures

黃河小浪底水利枢纽是黄河干流的关键控制性骨干工程，在黄河治理开发中具有十分重要的战略地位。为了满足以防洪（包括防凌）、减淤为主，兼顾供水、灌溉、发电等的开发任务需要，小浪底水利枢纽共设置了3条孔板洞、3条排沙洞、3条明流洞、6条发电洞和1条灌溉洞[1]，各隧洞设有工作、事故、检修闸门，控制各条泄水洞的进水“咽喉”，形成底部泄洪排沙、中间引水发电和上部泄洪排漂的格局[2]，担负着完成枢纽任务和确保工程安全的重要使命。

黄河来水含沙量高且来沙量大。小浪底水库运行至2019年10月，库区三角洲顶点高程已经达到212.70 m，顶点距坝里程约10.32 km。坝前1.32 km处淤积高程由137.50 m抬高至181.64 m，淤积抬升了44.14 m，高于最低进水口底板高程6.64 m;进水塔前60 m处淤积高程为176.18 m，高于最低进水口底板高程1.18 m。受泥沙淤积影响，有可能导致进水口淤堵、闸门启闭困难等。如2019年7月17日，在执行全关2号排沙洞事故闸门操作时，发现闸门底坎有厚约330 mm的淤积泥沙，致使无法全关到位。据统计，2018—2019年小浪底工程事故闸门启闭遇到的淤堵及卡阻问题达12次之多。

随着小浪底水库库区泥沙淤积发展，三角洲顶点进一步向坝前推进，淤积面不断抬高，泄水建筑物进水口泥沙淤堵的风险也越来越大，影响工程效益发挥和枢纽工程安全运行，开展小浪底水利枢纽进水塔群前防淤堵研究十分必要。目前已开展了一系列的模型试验研究[3-6]，并取得了一定的研究成果，但是物理模型试验的周期长，且对不同工况的灵活度较低。笔者利用立面二维数学模型，在典型设计水沙条件下对不同泄水孔洞运用方案的底孔防淤堵进行数值模拟研究，从河床纵剖面、排沙比、发电效益等方面综合分析比较，从而选定合理的泄水孔洞运用方案，为确保水库安全运行并充分发挥小浪底水库的工程效益提供技术支持。

1 立面二维数学模型及其控制方程

近年来三维水流数学模型发展迅速，可以直观准确地描述水流的细节运动[7-9]，但是其计算成本非常高，很难普遍应用于大尺度长历时的实际工程问题研究。一维水流数学模型适用于长历时长河段的计算，但其更侧重于物理量在各断面上的平均值，在某些特定的问题中难以反映物理要素在断面上的分布。综合而言，二维数学模型能够较好地平衡计算量和水流细节描述的问题。二维模型分为平面二维和立面二维模型，对于水库坝前段，伴随着水库泄水等调节控制运用，常有异重流发生，并且在孔口前易形成冲刷漏斗，不同深度的含沙量及流速差异明显。为进行小浪底水利枢纽进水塔群前的防淤堵研究和泄水孔洞的调度方案比选，宜采用立面二维数学模型进行模拟和计算研究。

根据流体力学的基本守恒定律，分别以水流、泥沙以及河床为研究对象建立各自的控制方程[10]。

水流连续方程：

ux+vy=0（1）

水流运动方程：

ut+uux+vvy=-1ρpx+νt（2ux2+2uy2）（2）

vt+uvx+vvy=-g-1ρpy+νt（2vx2+2vy2）（3）

悬移质运动方程：

hst+husx+h（v-ω）sy=ε（2hsx2+2hsy2）（4）

河床变形方程：

Zbt=Pγω（sa-s*a）γ′（5）

式中：x为沿水流方向坐标;y为垂直方向坐标，向上为正方向;u为沿水流方向流速;v为垂直方向流速;p为压强;ρ为清水密度;νt为紊流黏滞系数;h为水深;ε为泥沙紊动扩散系数;Zb为河床高程;ω为泥沙沉速;Pγ为泥沙孔隙率;s为含沙量;sa、s*a为床面含沙量及挟沙力;γ′为泥沙干容重。

为了使表示自由水面的水位函数ξ（x，t）和动量方程紧密联系起来，将压强分解为动水压强和静水压强之和，即p=pd+ps。pd为动水压强，是水体流动时因流线弯曲和流速不均匀所产生的附加压强;ps为静水压强，ps=ρg[ξ（x，t）-y]，将压强分解后，压强梯度可分别改为

-px=-pdx-ρgξ（x，t）x（6）

-ρg-py=ρdy （7）人 民 黄 河 2020年第10期

2 数学模型的求解

2.1 方程离散

水流运动方程离散采用基于交错网格离散的SIMPLE算法，如图1所示，标量变量和各种常数储存在网格节点上，矢量变量及速度变量储存在控制边界上。

水流运动方程可离散为

un+1i+1，j+1/2=uni+1，j+1/2-（uux+vuy）Δt+

[-1ρpx+νt（2ux2+2uy2）]Δt（8）

vn+1i+1/2，j+1=vni+1/2，j+1-（uvx+vvy）Δt+

[-1ρpy+νt（2vx2+2vy2）]Δt（9）

式中：Δt为时间步长;n为时间节点编号;i为x方向节点编号;j为y方向节点编号。

悬移质运动方程在矩形网格上采用有限体积法离散：

（hsk）n+1i+1/2，j+1/2-（hsk）ni+1/2，j+1/2Δt+

（hu）n+1i+1，j+1/2snki+1，j+1/2-（hu）ni+1/2，j+1/2snki，j+1/2Δx+（hv-hω）n+1i+1，j+1/2snki+1/2，j+1/2-（hu-hω）ni+1/2，j+1/2snki，j+1/2Δy=

CFFx-CFBxΔx+CFFy-CFByΔy（10）

式中：CFFx、CFBx、CFFy、CFBy为式（4）右端项的离散代数关系式，根据文献[11]进行求解。

CFFx=εhn+1i+3/2，j+1/2+hn+1i+1/2，j+1/22sni+3/2，j+1/2-sni+1/2，j+1/2ΔxCFBx=εsni+3/2，j+1/2+sni+1/2，j+1/22hn+1i+3/2，j+1/2-hn+1i+1/2，j+1/2ΔxCFFy=εhn+1i+1/2，j+3/2+hn+1i+1/2，j+1/22sni+1/2，j+3/2-sni+1/2，j+1/2ΔxCFBy=εsni+1/2，j+3/2+sni+1/2，j+1/22hn+1i+1/2，j+3/2-hn+1i+1/2，j+1/2Δx（11）

河床变形方程离散形式为

ΔZb=Pγω（sa-s*a）γ′Δt（12）

式中：ΔZb为河床冲淤厚度。

2.2 封闭模式

泥沙运动极其复杂，对于其中河底挟沙力公式需要采用经验公式来进行封闭。立面二维水沙数学模型计算中与河床冲淤变形相关的因素是河床底部含沙量与挟沙力，通常选一接近河底的点作为参考点，参考点距离河底为ξa=（0.01～0.05）h，河底挟沙力公式为

sb=s*（1+gck）j1-gckj2（1ξ-1）z1（13）

式中：s*為挟沙力;c为谢才系数，c=h1/6/n;j1、j2分别为计算参数，j1=∫1ξa[（1-ξ）/ξ]Zdξ，j2=∫1ξa[（1-ξ）/ξ]Zln ξdξ，其中Z为悬浮指标、ξ为水深;k为卡门常数;z1=ωβkU*=Zβ，其中β为参数、U*为摩阻流速。

2.3 模型计算网格

模型计算网格布置如图2所示。网格长度为50 m，高度为2 m，总数为90×50。

3 不同泄水孔洞调度方案比选

数值模拟的研究范围为小浪底水库库区大峪河口至大坝段，在距离进水塔4.5 km范围内设置了31个漏斗测验断面，断面编号自下而上依次为HHLD01—HHLD31，距塔210 m以内断面间距为50 m，距塔210～710 m范围内断面间距为100 m，距塔710 m以上断面间距为100～200 m。

3.1 典型设计水沙过程选取

20世纪80年代中后期以來，受人类活动和气候变化的影响，黄河来水来沙条件发生了较大变化，尤其是2000年以来水沙条件变化更为明显，来水来沙量大幅度减少。本次研究在1987年以来实测入库水沙过程的基础上选取入库水沙条件，从不利于进水塔前防淤堵的角度考虑，选取平水偏丰沙过程。

由于小浪底水库冲淤变化主要发生在汛期，因此针对7—9月对进水塔群前进行防淤堵模拟研究。通过对1987年以来7—9月三门峡站（入库控制站）的水沙过程分析，选取平水偏丰沙的2003年7—9月实测入库水沙过程作为入库的典型水沙条件。

为了提高模拟精度，立面二维模型常采用较为精细的计算网格，但是受计算能力限制，模拟范围往往局限于坝前区域。鉴于此，需要利用库区一维水沙数学模型提供的坝前4.5 km处的流量、输沙率过程，以此确定坝区立面二维水沙模型进口边界的流量和含沙量分布。

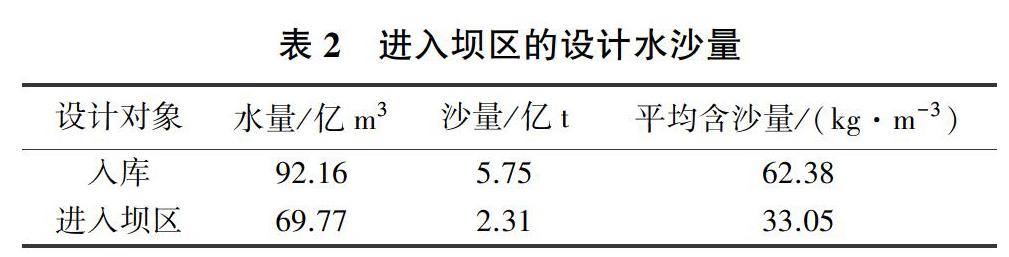
由于没有2003年的初始地形数据，因此基于2014年4月的初始地形资料，把2003年7—9月实测水沙过程作为计算条件，将计算结束后的地形作为库区立面二维水沙数学模型计算的河床初始边界条件，见表1和图3。其次，把2003年7—9月进入坝区的实测水沙过程作为立面二维模型所采用的设计水沙过程，其设计流量过程如图4所示，设计含沙量过程（该设计水沙过程以下简称为2003典型）见图5，设计水沙量见表2。进水塔前高程与底孔进口高程均为175 m。

3.2 泄水孔洞调度方案

底孔防淤堵研究拟对两种泄水孔洞调度方案进行比选。方案1：当出库流量小于发电洞泄流量时，优先启用发电洞泄流;当出库流量超过发电洞泄流量时，超出部分尽量通过排沙洞、明流洞、孔板洞泄流，减少库区淤积。方案2：出库流量大于400 m3/s时，发电洞过水80%，排沙洞分流20%。具体调度方案见表3。

3.3 数值模拟结果分析

采用库区立面二维水沙数学模型，分别对2003典型水沙条件下泄水孔洞调度方案1和方案2进行计算和分析比较，提出推荐的泄水孔洞调度方案。

3.3.1 河床纵剖面分析

两种泄水孔洞调度方案的河床淤积厚度和淤积量计算结果见表4，2003典型方案1和方案2河床纵剖面冲淤变化对比如图6所示。总体而言，两个方案计算结果差别不大，方案1和方案2在塔前约600 m范围均形成冲刷漏斗，塔前60 m处与初始时刻（7月1日）相比淤积厚度分别为1.40 m和0.42 m，塔前4 500 m处与初始时刻相比淤积厚度分别为11.41 m和11.29 m。7月1日—9月30日，整个计算范围平均淤积厚度分别为8.87 m和7.96 m，方案1与方案2相比，平均淤积厚度多0.91 m，坝区淤积量多424万m3。

图7为方案1塔前60 m处淤积高程与出库流量变形过程。7月1日—8月30日只有发电洞过流，塔前60 m处持续淤积抬高，最大值达到181.39 m;9月1日—9月30日除了发电洞开启，排沙洞也有开启，塔前60 m处持续降低。

图8为方案2塔前60 m处淤积高程与出库流量变化过程，7月1日—7月10日发电洞过流80%，排沙洞过流20%，在此期间来沙较少，塔前60 m处略有淤积抬升，7月11日—8月31日只有发电洞过流，塔前60 m处持续淤积抬高，最大值达到181.35 m，9月1日—9月30日除了发电洞开启，排沙洞也有开启，塔前60 m处持续降低。

方案1与方案2不同之处在于，方案1出库流量小于1 800 m3/s（6台机组满发）时全部通过发电洞下泄，方案2出库流量为400～2 250 m3/s时发电洞过流80%、排沙洞分流20%。当出库流量大于2 250 m3/s时，两方案的孔洞运用方式相同。方案2排沙洞开启的时间略长，有利于排沙。模拟时段内底孔前淤积高程均没有达到允许淤积高程187 m。

3.3.2 排沙比

2003典型7月1日—8月31日进入坝区的沙量为1.44亿t，方案1计算的出库沙量为0.98亿t、排沙比为68.1%，方案2计算的出库沙量为1.02亿t、排沙比为71.0%，方案2比方案1多排沙0.04亿t。7月1日—9月30日进入坝区的沙量为2.31亿t，该时段内方案1出库沙量为1.84亿t、排沙比为79.9%，方案2出库沙量为1.89亿t、排沙比为81.9%，方案2比方案1多排沙0.05亿t，见表5。

3.3.3 发电效益

水轮机发电量可表示为

N=9.81ηQH（14）

式中：Q为通过水电站水轮机的流量;H为水电站的净水头;η为水电站效率。

经计算，2003典型方案1总发电量为11.57亿kW·h，方案2总发电量为10.65亿kW·h，方案1比方案2多发电0.92亿kW·h，见表6。

3.3.4 泄水孔洞调度方案推荐

综上，虽然方案1比方案2进水塔前平均淤积厚度多0.91 m，但是两方案在模拟时段内底孔前淤积高程均未达到允许值187 m，都能保证进水塔群前实现防淤堵的要求。在此前提下，方案2底孔开启次数多，使得方案2发电效益不如方案1，为充分发挥水库的发电效益，推荐选用泄水孔洞调度方案1。

4 结 语

将建立的立面二维水沙数学模型应用于小浪底水利枢纽进水塔群的防淤堵研究，在典型设计水沙条件下，计算和比较了两种泄水孔洞调度方案下河床纵剖面的变化及其对排沙比和发电效益的影响，得出以下结论。

（1）在模拟时段内，方案1和方案2的底孔前淤积高程均未达到允许值187 m。

（2）就平均淤积厚度而言，方案1比方案2在进水塔前多淤积0.91 m;就排沙比而言，在同时段方案2比方案1稍高，但方案2底孔开启次数多，发电效益不如方案1。

（3）在满足近期进水塔群防淤堵要求的前提下，应尽可能发挥小浪底水库的发电效益，泄水孔洞调度方案推荐选用方案1，即出库流量小于发电洞泄流量时优先启用发电洞泄流，出库流量超过发电洞泄流量时超出部分尽量通过排沙洞、明流洞、孔板洞泄流，减少库区淤积。

参考文献：

[1] 王二平，张欣，孙东坡，等.小浪底水利枢纽防泥沙淤堵试验研究[J].华北水利水电大学学报（自然科学版），2015，36（6）：6-9.

[2] 林秀山.黄河小浪底水利枢纽文集[M].郑州：黄河水利出版社，2001：1-6.

[3] 邢晨雄.小浪底浑水动床模型验证及进水塔前冲刷漏斗试验研究[D].郑州：华北水利水电大学，2016：17-22.

[4] 王银海.高水位水库淤积泥沙水力排淤模拟研究[D].郑州：华北水利水电大学，2018：9-12.

[5] 张欣.小浪底枢纽进水塔前允许淤沙高程试验研究[D].郑州：华北水利水电大学，2016：9-14.

[6] 何胜男.小浪底水利枢纽进水塔群高滩边岸坍塌特性试验研究[D].郑州：华北水利水电大学，2016：9-14.

[7] 刘子龙，王船海.复杂边界准三维水流模拟[J].成都科技大学学报，1996，28（1）：12-20.

[8] 李褆来，窦希萍，黄晋鹏.长江口边界拟合坐标的三维潮流数学模型[J].水利水运科学研究，2000（3）：1-6.

[9] 周宜林，道上正规，桧谷治.非淹没丁坝附近三维水流运动特性的研究[J].水利学报，2004，35（8）：46-53.

[10] 余明辉，吴腾，杨国录.剖面二维水沙数学模型及其初步应用[J].水力发电学报，2006，25（4）：66-69.

[11] 余明辉，杨国录.平面二维非均匀沙数值模拟方法[J].水利学报，2000，31（5）：65-69.

【责任编辑 张 帅】