超混沌Rossler系统与分数阶超混沌Chen系统的异结构同步分析

杜永霞 高 雅 李珊珊

（河套学院数学与计算机系 内蒙古巴彦淖尔 015000）

一、引言

随着混沌系统研究的不断发展，人们提出了各种不同的混沌同步的方法，如驱动响应同步、主动控制同步、自适应同步等，这些方法在理论和实验上都已经有了广泛的应用。但这些理论大多是只研究了整数阶或者分数阶的同步问题，而分数阶和整数阶间的同步却发展的远不如整数阶充分。

本文基于追踪器的思想，利用分数阶系统的稳定性理论和主动控制方法实现了整数阶超混沌Rossler系统和分数阶超混沌Chen系统的同步，理论分析和数值仿真结果的一致性表明了同步方法的有效性。

二、系统描述

超混沌Rossler系统的是数学模型为：

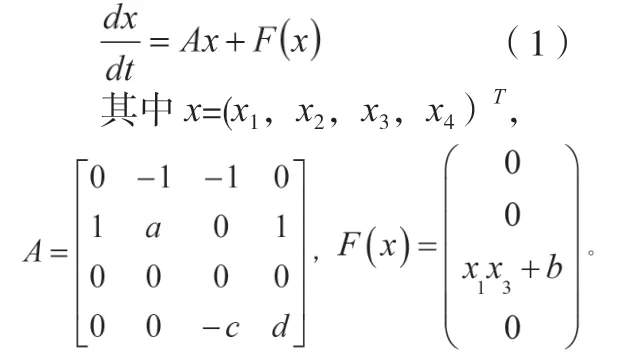
当a=0.25,(b=3,c=0.05,d=0.05时，系统呈现超混沌现象。

分数阶超混沌Chen系统的数学模型为

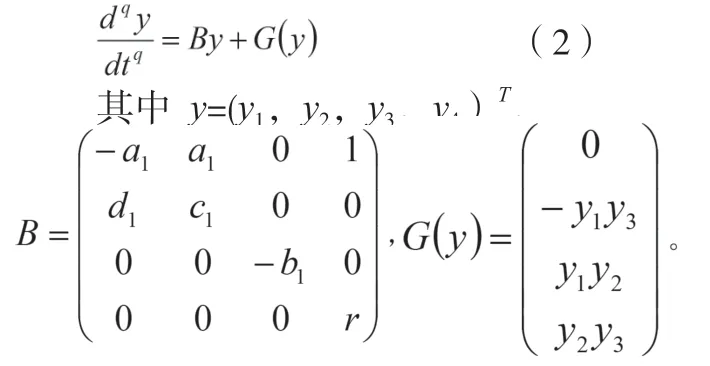
当a1=35,b1=3,c1=12,d1=7,r=0.5,q=0.95时，此时系统是超混沌的。

在（3）式中u(x）+U(t）为追踪控制器，u(x）为补偿器，U(t）为控制器。

定义受控系统（3）中的补偿器u(x）为

三、主动控制同步

定理1：假设存在关于e1,e2,e3,e4）函数的控制输入信号V1(t）,V2(t）V3(t）,V4(t），若控制函数选择为

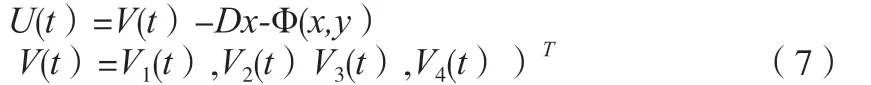
则分数阶超混沌Chen系统与超混沌Rossler系统渐近同步。

证明 将方程（7）带入到误差系统（6），得到如下的误差系统：

因为V(t）=V1(t）,V2(t）V3(t）,V4(t））T是关于误差函数 的控制输入信号，即V(t）=Ke

其中K∈R4×4实常数矩阵，关于矩阵K∈R4×4的选取有很多种可能情况。

该式满足同步条件，故实现了分数阶超混沌Chen系统和超混沌Rossler系统的异结构同步。

通过数值模拟实验验证此方法的有效性，取a=0.95时，选取参数为：(a,b,c,d）=(0.25,3,0.5,0.5)，(a1,b1,c1,r）=(35,3,12,7,0.5)，初值选择为：(x1(0),x2(0),x3(0),x4(0))=(3,-4,2,2)， (y(0),y(0),y(0),y(0))=(-15,5,9,3-4,18.6)