极靴形状对永磁副励磁机工作性能的影响

刘韬伦， 辛绍杰

(上海电机学院 机械学院， 上海 201306)

近年来，三级式无刷励磁系统越来越多地应用到汽轮发电机组中，其最大优点是取消了大电流集电环和电刷，从而克服了高速器制造和大电流集电环通流的问题[1]，并且大大降低了维护、运行和检测的成本，具有很高的可靠性[2]。而永磁副励磁机作为永磁同步发电机的一个应用方向，专门为大型汽轮机组提供励磁，作为三级式无刷励磁的第一个环节，其工作效率直接决定了汽轮发电机的工作效率,对整个励磁系统甚至最终的发电效率都有着重要作用[3]。

对于发电机电磁场的数值分析方式主要有有限元法、边界元法和有限差分法3种。与其他两种方法相比，有限元法具有计算时间短、几何剖分灵活、程序标准化等优点，故有限元法是目前最有效且应用最广泛的分析方式[4-6]。

极靴是永磁副励磁机不可缺少的一部分，可有效改善副励磁机工作时的磁感线分布状况，使其工作效率更高。极靴的形状对气隙磁密的影响体现在气隙磁密的基波幅值和谐波畸变率均受偏心极弧半径Rp的影响较大，且偏心极弧半径Rp减小会使气隙磁密基波幅值受到削弱，并且存在一个使气隙磁密谐波畸变率较小的区域[7-8]。本文针对一台无刷永磁副励磁机，以有限元软件Maxwell为基础，建立了永磁副励磁机的两种物理模型，施加边界条件求出其空载特性；通过对额定参数的计算确定等效额定负载，从而模拟出在额定负载下的工作特性[9-11]；对极靴进行参数化建模，通过比较得到发电机运行性能最优时对应的极弧系数[12-13]。

1 原理与计算方法

1.1 空载特性

永磁副励磁机是永磁同步发电机的一个分支，具有与永磁同步副励磁机相同的磁路计算方法。空载运行时，空载气隙基波磁通在绕组中产生励磁电动势E0；负载运行时，气隙合成基波磁通在定子线圈中产生气隙合成电动势Eδ，即：

E0(V)=4.44fNKdpΦδ0KΦ

(1)

Eδ(V)=4.44fNKdpΦδNKΦ

(2)

式中：N为电枢绕组每相串联匝数；Kdp为绕组因数；KΦ为气隙磁通的波形系数；ΦδN为每极空载气隙磁通，Wb；Φδ0为每极气隙合成磁通，Wb。

每极空载气隙磁通和每极气隙合成磁通可用等效磁路法求出。

空载时：

(3)

(4)

Φδ0=(bm0-hmoλσ)BrAm×10-4

(5)

负载时：

(6)

(7)

ΦδN=(bmN-hmNλσ)BrAm×10-4

(8)

式中：bm0为空载时永磁体工作点磁通密度标幺值；φm0为空载时每极磁通标幺值；hm0为空载时永磁体工作点退磁磁场强度标幺值；fm0为空载时永磁体向外磁路提供的磁动势标幺值；Br为剩磁密度；bmN为额定工况下永磁体工作点磁通密度标幺值；φmN为负载时永磁体向外磁路提供的磁动势标幺值；hmN为额定工况下永磁体工作点退磁磁场强度标幺值；fmN为负载时永磁体向外磁路提供的磁动势标幺值；f′为每对极磁路中等效电枢磁动势的标幺值；Am为永磁体提供每极磁通的截面积；λn为外磁路合成磁导标幺值；λσ为漏磁导标幺值，则

λn=λσ+λδ=σ0λδ

(9)

式中：λδ为主磁导标幺值；σ0为空载漏磁系数，即

(10)

本文所采用的磁路结构为径向结构，即有

Am=bMLM

(11)

式中：bM为永磁体宽度；LM为永磁体轴向长度。

(12)

式中：fad为直轴电枢反应的标幺值；Fad为每极直轴电枢磁动势；Hc为工作温度时的计算矫顽力；hMp为永磁体每对极磁化方向长度，对径向结构有

hMp=2hM

(13)

式中：hM为永磁体磁化方向长度，即厚度。

固有电压调整率对于永磁副励磁机来说也是非常重要的指标，是指在转速一定时电压随负载的变化情况，其数值只取决于发电机本身的特性。作为永磁同步发电机的一个分类，永磁副励磁机制成后气隙磁场调节同样非常困难，为了能将其大量推广，有必要对其固有电压调整率有一定要求：

(14)

式中：U为输出电压；UN为额定相电压；E0为空载励磁电动势。

在理想状况下，电压波形应是周期性标准正弦波，但由于线圈绕组会提供感性阻抗，所以最终输出的波形会偏离正弦波产生畸变。电压畸变率过高会导致设备过热等不良现象，也应作为优化指标来考虑。

电压畸变率计算方法为

(15)

式中：Un为第n(n=2,3,…,n)次谐波电压有效值；U1为基波电压有效值。

1.2 额定负载计算

通过副励磁机的额定电压、额定电流与功率因数得出额定负载时的等效阻抗，采用场路耦合的方法来模拟无刷副励磁机的额定负载工况，可以提高计算收敛性：

(16)

式中：Z为每相额定等效阻抗；UN、IN为额定电压和额定电流；φN为功率因数角；R为每相额定等效电阻；L为每相额定等效电感；ω为角频率。

图1所示为搭建外电路，与电磁场模型进行耦合，其中LWinding A、LWinding B、LWinding C分别是与有限元模型耦合的三相定子绕组。端部漏抗远远小于负载阻抗，可忽略不计。

图1 额定等效负载外电路

2 建模与电磁场仿真

2.1 Maxwell 2D建模

本文选用的永磁副励磁机主要参数如表1所示。

表1 永磁副励磁基本参数

在有限元软件Maxwell 2D环境下建立永磁无刷副励磁机二维瞬态场模型[14]。

本文研究对象采用内转子外定子的结构形式，副励磁机定子有60个槽，且定子槽为梨形槽，槽内采用双层绕组。定子槽模型如图2所示，为了提高磁密和改善磁场分布，对定子槽模型进行90°折线处理。

图2 定子槽

2.2 求解域和边界条件设定

在建模后，为了求解的精度和时间都能够最佳化，取两个磁极为求解区域(一个电周期)，如图3所示。

图3 副励磁机求解区域

为顺利进行仿真分析工作，对发电机做出如下假设：

(1) 对磁极冲片和定子槽形状作近似处理；

(2) 将每个槽内双绕组的数根导线近似为两块导体；

(3) 忽略端部影响。

施加如下边界条件：

(1) 取外壳矢量磁位为零，施加狄里克莱边界条件[15]：

(18)

式中：Az为矢量磁位；Js为源电流密度；μ为磁导率。

(2) 在扇形区域的两条半径上施加主、从边界条件：

Bs=Bm

(19)

式中：Bs为主边界磁密；Bm为从边界磁密。

2.3 剖分网格

在有限元计算过程中，网格的剖分是一个非常重要的环节，网格的合适与否直接决定了计算的精准度和准确度。设置的网格太多，会导致计算机资源的浪费，也会耗费一些不必要的时间；设置的网格太少，则可能导致一些重要的区域(如气隙)的剖分结果不够精细，从而降低结果的准确率。因此，有必要选择合适的剖分单元。

Maxwell 2D具有自适应网格剖分功能，在分析模型时，有限元软件可以自动确定网格单元，但自适应网格剖分下网格质量不高，数量不够多，为此有必要对每个部分设定参数，重新剖分网格。改善后额定网格剖分如图4所示。

图4 改善后的网格剖分

3 有限元仿真结果分析

3.1 空载仿真结果

永磁无刷副励磁机空载运行时的磁场分布状况对副励磁机的电磁设计而言非常重要，可以直接影响副励磁机的感应电势、转矩、功率等参数。空载气隙径向磁密分布如图5所示。

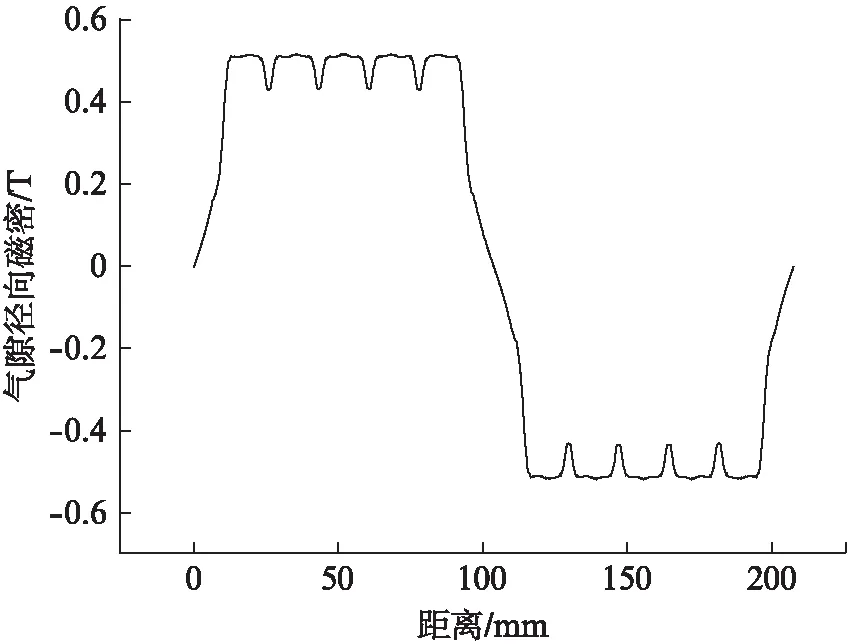
图5 空载气隙径向磁密分布

永磁副励磁机空载运行时，所得空载感应电压如图6所示，经过傅里叶变换后可以得到基波感应电压幅值为131.65 V，计算后得到副励磁机空载相电压为161.23 V。

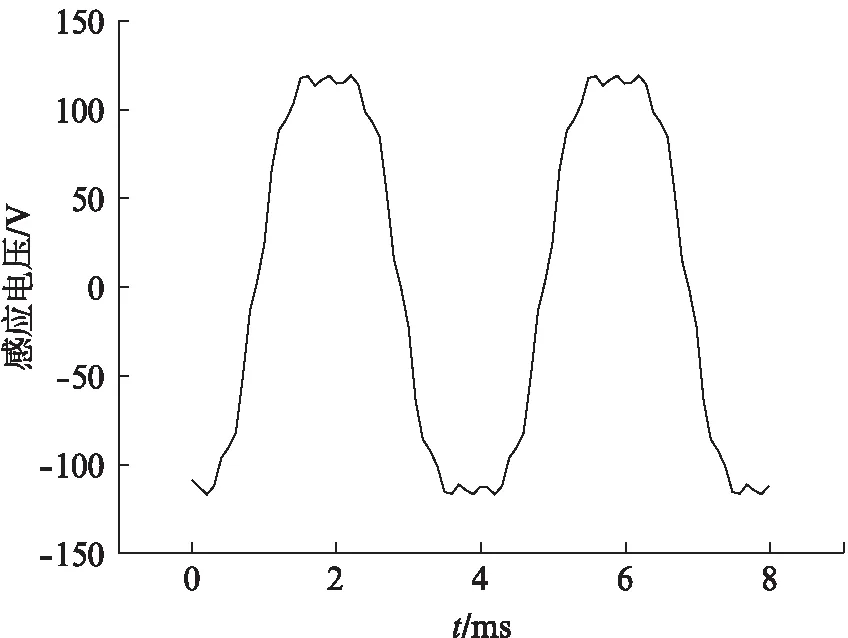
图6 二维模型下的空载电压

3.2 满载仿真结果

通过计算得出等效负载搭建外电路，并将其与电磁场进行耦合，可以模拟出额定负载下副励磁机的工作情况。此时的气隙磁密情况如图7所示。

图7 额定负载下的气隙径向磁密

从图7可以看出，在额定工况下，同一块极靴所对应的径向磁密随距离减小。

额定负载下的感应电压及感应电流如图8所示。经过傅里叶变换后可以得到基波感应电压幅值为127.76 V，即输出相电压为156.49 V。

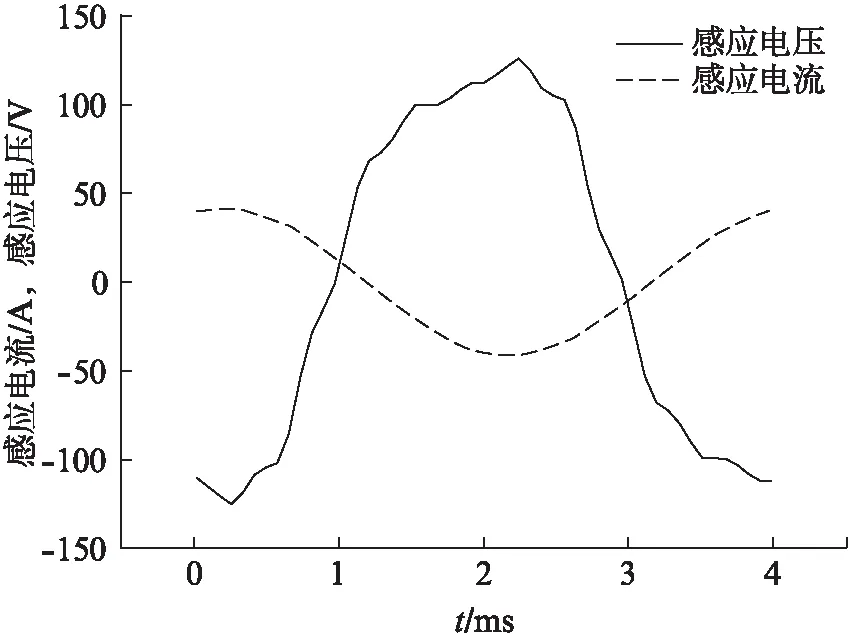
图8 二维模型下的额定电压及电流

4 电磁场优化

4.1 极弧系数

在永磁副励磁机中，极靴宽度太小会导致无法改善磁感线分布，太大则会导致漏磁与损耗增大。出于以上考虑，极弧系数调整范围取0.7～0.8。

通过对极弧系数的计算，可以得到相对应的极靴宽度范围在72～81 mm之间。对极靴宽度进行参数化设置，以极靴宽度的一半作为变化量，设置范围为36～40.5 mm，步长为0.5 mm，如图9所示。

图9 参数化建模设置

仿真运行结束后得到电压随时间变化的曲线，对空载电压仿真结果进行傅里叶变换，可以得到不同极靴宽度下空载电压的基波幅值情况，如表2所示。

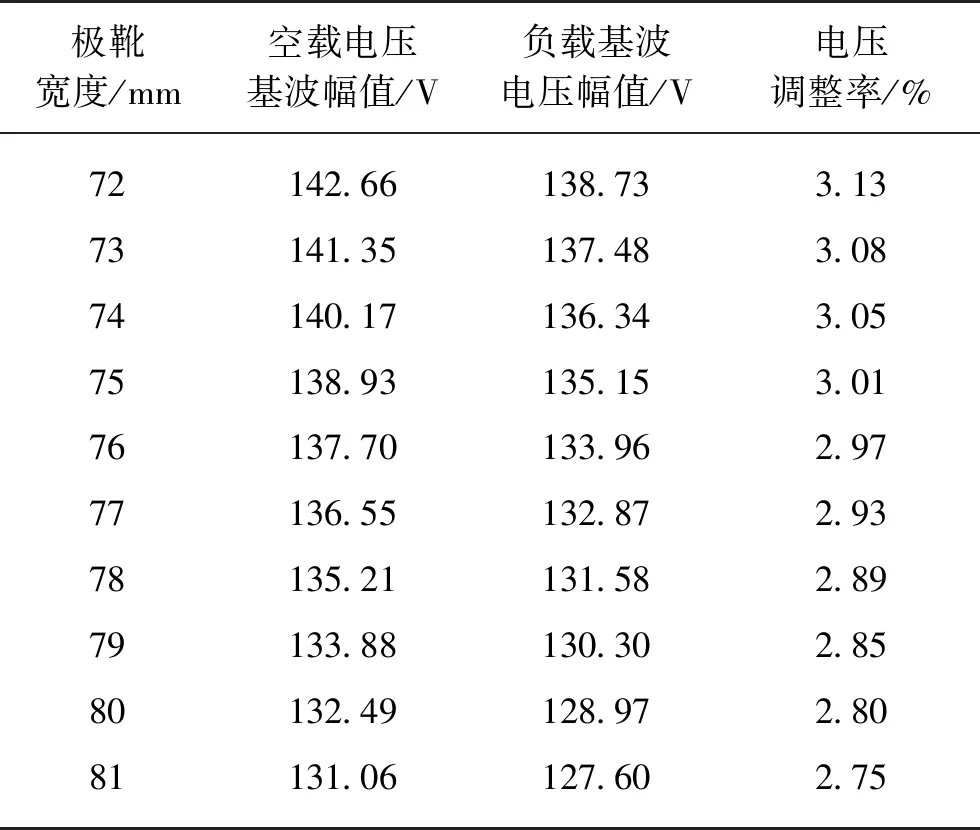
表2 不同极靴宽度下空载电压的基波幅值

由表2可见，在其他条件不变的情况下，极靴宽度对副励磁机固有电压调整率影响不大。

空载电压畸变率如图10所示，随着宽度增加，电压畸变率增加幅度较大，即极靴过宽时永磁副励磁机的输出电压波形较差。

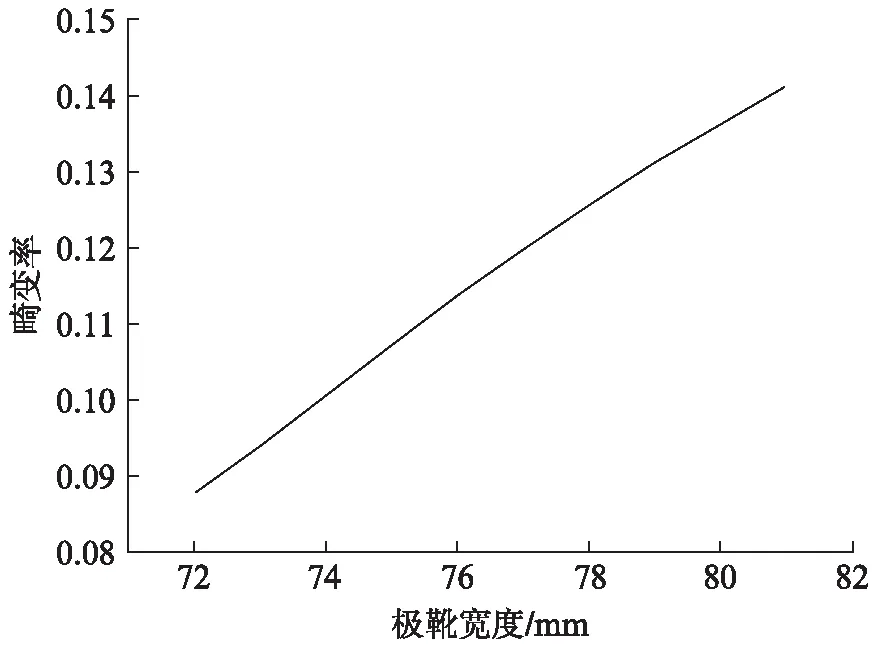
图10 电压畸变率与极靴宽度关系

通过对副励磁机的气隙谐波和空载电压分析可得：当极靴宽度取72 mm，即极弧系数为0.7时，电压调整率与电压正弦畸变率最佳，此时副励磁机拥有最佳的运行性能。

4.2 偏心距

以同样的处理方法对极靴弧形做参数化处理，来模拟偏心距不同时副励磁机的运行性能结果。以极靴宽度为80 mm作为实验对象，取偏心距范围为0～60 mm,步长为10 mm，共7组数据。对应的电压调整率和空载电压畸变率变化趋势如表3所示。

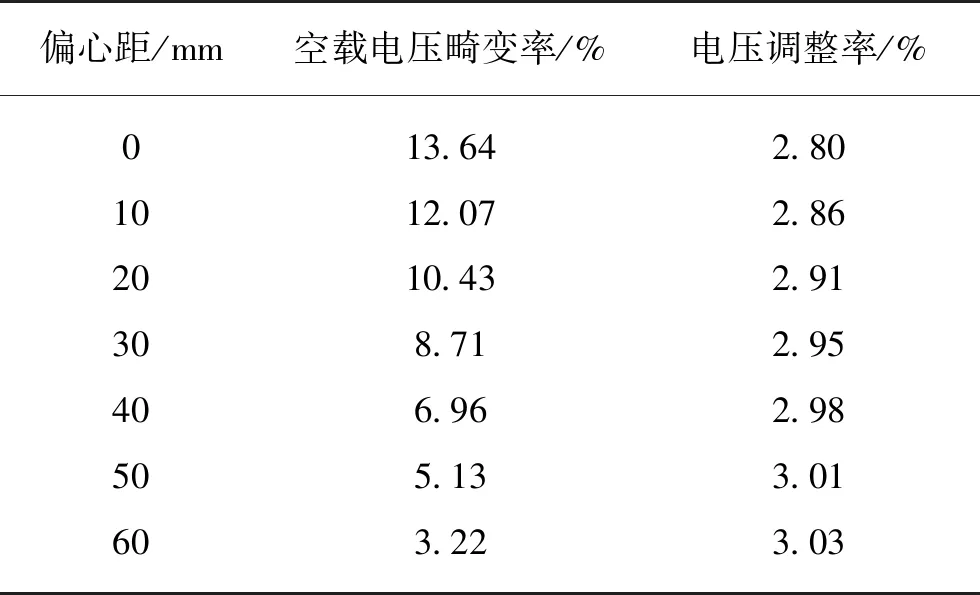
表3 不同极靴宽度下空载电压的基波幅值

由表3可知，随着偏心距的增大，空载电压畸变率不断减小，电压调整率增大，但由于空载电压调整率变化趋势远大于电压调整率，故偏心距为50 mm时副励磁机运行性能最佳。

5 结 语

本文以一台7.8 kVA额定容量的钕铁硼永磁副励磁机进行了建模仿真及计算，分别研究了其在空载、满载两种工况下的气隙磁密、磁场分布、感应电势情况，通过场路耦合来模拟出在额定负载下的感应电流。针对永磁副励磁机的电压调整率与空载电压正弦畸变率的问题，选取了不同的极弧系数与偏心距做了对比分析。结果表明，当极弧系数为0.7，偏心距为50 mm时，气隙谐波和反电势数值最小，永磁副励磁机具有最佳运行性能。