基于决策树的无车承运人平台货运任务定价模型

汪琼枝，马永传

(皖西学院 金融与数学学院，安徽 六安 237012)

无车承运人是由美国track broker(货车经纪人)这一词汇演变而来[1]，是无船承运人在陆地的延伸，指的是不拥有车辆而从事货物运输的个人或单位。其一般不从事具体的运输业务，只从事运输组织、货物分拨、运输方式和运输线路的选择等工作[1]，已经有成熟的运行模式，具有多项优势[2]。无车承运人平台有三个参与角色：平台、货主、承运人。其利用互联网平台连接货主和承运人，通过有效对接货主与承运商的需求并促使其交易，极大改善了物流业资源闲置率高的状况[3]。在其运行模式中，首先货主在平台发布货运任务；接着平台根据任务条件，给出货运任务指导价格；最后承运人浏览任务，根据任务线路和价格自主选择承运任务。如果平台指导价格科学合理，能够促进货运任务快速成交，增加货运任务交易的成功率，货主、承运人、平台三方均能获益，从而提高平台运行的整体效率。因此，如何对无车承运人平台货运任务科学定价，具有很强的研究价值和现实意义。

随着我国无车承运人平台的兴起，国内也出现了一些相关研究。尤美虹、骆温平、陶君成通过实地访谈和网络调查[3]，调查分析了平台监管问题。董娜综合分析了平台的内涵、优势，提出了未来发展的建议[1]。金忠旭和郭跃显利用物联网等新技术，提出了基于互联网+平台的物流模式[2]。冯淑贞分析了发展现状和相关的政策与制度问题[4]。张树山课题组研究了平台绩效动态演化的趋势，构建了绩效演化的系统动力学模型[5]。基于普通公路货运定价已经有了一些相关研究。顾敬岩和吴群琪[6]研究了我国公路货运价格的演化趋势，并提出了一些政策建议。王燕凌通过数据统计，分析了我国公路货运市场的供求[7]。陈艳静分析了公路货运价格的影响因素，并给出了一些的完善运价形成机制的对策和建议[8]。冯芬玲和李杰潞分析了公路和铁路的货运价格和服务竞争，并建立了铁路货运和公路货运的Hoteling模型[9]。但是，无车承运人平台货运任务定价模型的相关研究还很少。王聪珊等人给出了一个多元线性回归模型，预测了平台货运定价[10]。聂福海和李电生基于信息不对称理论，从博弈的角度研究了平台的定价策略[11]。

决策树是一种非线性监督机器学习，常用于分类和回归[12]。其原理是通过从训练集数据学习简单推测规则，来预测目标变量的值。决策树具有诸多优点：易于理解和应用、需要较少的数据预处理、预测算法为对数复杂度，训练速度快、出色的数据分析效率、直观易懂的结果展示[12]。决策树有多个算法，其中CART(Classification and Regression Trees)决策树算法由L. Breiman, J. Friedman, R. Olshen, and C. Stone提出[13]，是一种广泛应用于分类和回归的决策树算法[14]。CART决策树的回归预测效果很好，已广泛应用于多个领域，并取得了良好的效果。李晓宁等人利用CART决策树预测平原河网区不透水面覆盖度[15]。董红召利用CART决策树预测城市交通道路氮氧化物浓度[14]。韩家琪等人利用CART决策树预测土壤水分[16]。许安定等人利用CART决策树预测烤烟评吸质量[17]。探索使用CART决策树来建立无车承运人平台货运任务定价模型，预测无车承运人平台货运任务价格具有良好的理论基础和实际应用意义。

Pandas 是 Python 的核心数据分析支持库，主要用户数据整理与清洗、数据分析与建模、数据可视化与制表，具有高效、易用等特点，是目前流行的开源数据处理库。

本文首先利用pandas库分析了平台货运任务价格的主要影响因素，接着提出了一种基于CART决策树的定价模型，预测平台新任务价格，最后利用某无车承运人平台的实际运行历史交易数据，验证模型的有效性，并与多元线性回归算法进行对比，验证了模型的优越性。

1 无车承运人平台货运任务价格的影响因素分析

要想准确的预测无车承运人平台货运任务的价格，首先需要找出影响平台货运任务价格的主要因素。

1.1 无车承运人平台货运任务价格的影响因素调研

通过调研现有的文献并结合某无车承运人平台的实际运行数据[6-9]，我们找出了可能对平台货运任务价格有影响的因素如下：

1)线路里程，线路里程是任务价格的直接影响因素，路程越长，成本越高，相应价格很可能越高。

2)业务类型(速运或重货)，一般来说，重货的成本要大于速运，相应价格可能越高。

3)是否区域发运，一般来说，区域发运的成本更低，相应价格可能越低。

4)计划还是临时，从博弈的角度考虑，临时任务的价格可能更高。

5)车辆长度，车辆更长的货车载重更多，相应价格可能越高。

6)车辆吨位，车辆吨位更大的货车载重更多，相应价格可能越高。

7)运输等级，即线路等级，路况不同，收费站不同等等，也会影响大价格。

8)紧急程度，从博弈的角度考虑，越紧急的任务价格可能更高。

对平台以上因素的运行数据，我们首先需要进行量化处理。其中线路里程、车辆长度、车辆吨位数据、运输等级可以直接使用。业务类型，是否区域发运，计划还是临时为二元数据，我们均将其转化为数值0、1度量。紧急程度的原始数据为常规、紧急、特急，可将其转化为数值0、1、2来度量。

接着，我们需要分析以上因素及实际运价之间的相关性。利用pandas库，我们得出各影响因素及实际运价的相关系数如表1所示：

表1 影响因素及实际运价的相关系数

由表1可以得出：

1)车辆长度和车辆吨位相关性很高(0.99)。直观上，我们也认为货车越长，其载重量也越大。因此，这两个因素，我们去除和价格相关性更低的车辆长度因素，保留车辆吨位因素。

2)车辆吨位和里程数相关性很高(0.816)。我们分析认为，这两者缺少因果关系，因此两个因素均保留。

1.2 基于灰色关联度分析的货运任务价格的影响因素分析

灰色关联度分析法(Grey Relation Analysis, GRA)基于灰色理论分析系统因素间的相异程度[18]，通常用关联系数来表示因素间关联程度的大小[19]。方法具有对数据要求低、计算简单等优点。因此，我们利用灰色关联度分析来找出影响平台货运任务价格的主要因素。其具体过程如下：

1)确定自变量和因变量：我们用排除车辆长度后剩余的七个影响因素作为自变量，平台货运任务价格作为因变量。

2)归一化处理：由于各数据量纲不同，我们采用最大最小化方法进行数据归一化处理。

3)计算灰色关联度：

设Xi=(xi(1),xi(2),…,xi(n)),i=1,2,…,m为平台货运任务价格的影响因素。Y=(y(1),y(2),…,y(n)) 为对应的平台货运任务成交价格。

γ(Y,Xi)为Y与Xi的灰色关联度，则

(1)

其中

(2)

式(2)中ξ∈(0,1)为分辨系数。

其中灰色关联度的计算步骤可细化如下：

Step 1：根据(3)式对平台货运任务价格的影响因素序列进行初始化：

(3)

Step 2：根据(4)，(5)式，计算平台货运任务价格的影响因素序列的差：

其中，

(5)

Step 3：根据(6)，(7)式求Δi(k)中的最大值M与最小值m：

Step 4：根据(8)式计算关联系数：

(8)

Step 5：根据(9)式计算灰色关联度：

(9)

根据灰色关联度算法，计算得出七个影响因素的灰色关联度，如表2所示。

表2 货运任务价格的灰色关联度

根据表2的结果，线路里程、区域发运、紧急程度、计划或临时对任务价格的影响程度很高，这也符合实际情况。

1)线路里程直接影响到运送的成本，里程数的增加增大了运送的成本，从而增加了最终运价。表1也表明了，里程数和实际运价有很强的正相关性。

2)紧急程度的增加，临时的运输任务，都会减少了愿意接单的承运人数量，从而增加了最终运价。表1也表明了，这两个因素与实际运价的正相关性。

3)区域发运，可以降低运输成本，从而降低了最终运价。表1也表明了与实际运价的负相关性。

4)业务类型分为速运(1)和重货(0)，其中速运的成本要小于重货，从而减少了最终运价。表1也表明了这种负相关性。

5)运输等级与最终运价的关联度不高，此因素可以去除。

最终得出平台货运任务价格的六个主要影响因素如下：线路里程、是否区域发运、紧急程度、计划或临时、车辆吨位、业务类型。

2 基于CART决策树的无车承运人平台货运任务定价模型

我们采用CART决策树，构建无车承运人平台货运任务定价模型，具体流程如下：

1)特征选取

选取上一章总结的六个运价主要影响因素为特征向量。

2)CART决策树的生成

从根节点开始，从把所有训练集数据放到根节点开始，通过选择最佳特征，递归的将训练集数据划分到左右子集，即决策树的左右分枝。

其划分的过程如下：

Step 1：假设训练集数据的容量是n，输入变量为x，输出变量为y。当选择第j个特征向量x(j)及其取值v作为划分特征和划分点时，其两个子集(子树)定义如下：

式中，Rl(j,v)表示使用第j个特征变量及其取值v，划分出的左子树。Rr(j,v)表示使用第j个特征变量及其取值v，划分出的右子树。

Step 2：按(12)，(13)，(14)式求得最优划分的特征变量j及划分点v：

式中，yi表示输入变量xi对应的输出变量，xi∈Rl(j,v)表示使用第j个特征向量的取值v进行划分，属于左子树的输入变量。通过遍历所有输入变量，找到最佳划分变量j和最佳划分点v并构成一对(j,v)，然后依次将集合划分至两个子集。

Step 3：递归的进行上述划分过程，直到满足停止条件。

按照上述过程，我们实行了无车承运人平台货运任务定价模型，下一步我们将使用某平台实际数据来训练模型，测试效果。

3 数据和模型验证

3.1 实验数据

我们使用了某无车承运人平台历史运行数据，共16016条货运任务来进行实验。这些数据包括了任务id、线路里程、业务类型、是否区域发运、计划或临时、线路编码、线路指导价、线路成交价、交易时间、车辆长度、车辆吨位、运输等级、紧急程度等数据。根据第二章的研究，我们选取其中主要的六个影响因素的数据，将数据按8∶2的比例，采用随机分配为训练集和测试集。

3.2 评价标准

为了检验定价模型的效果。我们使用常用的误差指标：均方误差根(RMSE)和R-平方(R2)，并和传统的多元线性回归算法进行对比。

均方根误差，是通过观测值与真值偏差的平方与观测次数n的比值的平方根来度量模型误差，我们根据(15)式来进行计算。

(15)

我们根据(16)式计算R-平方，用其来判断模型的拟合程度，R-平方值越接近1说明拟合程度越好。

(16)

3.3 实验结果

我们的基于CARTR决策树的无车承运人平台线路定价模型，对数据集进行了5次随机划分，分别进行了训练和测试，实验结果如表3所示。

表3 基于CARTR决策树的无车承运人平台线路定价模型实验结果

作为对比，我们使用多元线性回归算法，以同样的训练集和测试集划分，也分别进行了训练和测试，实验结果如表4所示。

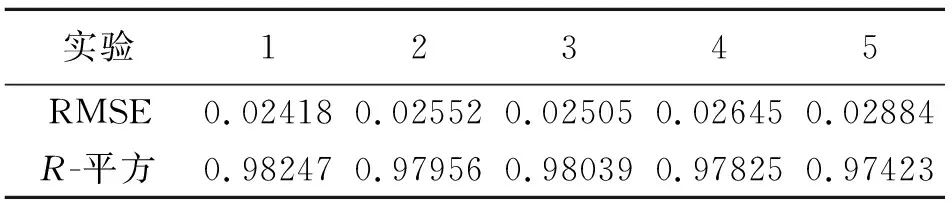
表4 多元线性回归实验结果

从表3和表4可以看出，相对于多元线性回归算法，我们模型的RMSE值均较小，且R-平方值均较大。结果验证了模型的有效性和优越性。

4 结论与展望

本文针对无车承运人平台的货运任务定价问题，分析了平台货运任务价格的主要影响因素，提出了一种基于CART决策树的定价模型，主要工作如下：

1)分析得出了平台货运任务运价的主要影响因素。

2)完成了整个定价模型的构建。

3)通过真实数据实验验证了模型的有效性，对比实验结果表明了该模型优于多元线性回归算法。

本文基于CART决策树的无车承运人平台的货运任务运价模型的提出，丰富了运价模型相关的理论研究。同时，货运任务运价模型能够帮助平台更为准确地给出任务的指导定价，促进了平台任务的快速成交，提高了平台的整体效率，提高了货主、承运人用户的使用体验，具有良好的现实意义。

进一步的研究包括，寻找更好的定价因素，以及更优的拟合算法，以其获得更好的定价预测。另外，当平台任务过多后，平台会面临信息过载问题，此时准确的货运任务定价并不能完全解决承运人快速寻找合适任务的问题，未来的研究可以考虑通过个性化任务推荐来解决平台信息过载问题。