一类带切换的随机SIRS模型的稳定性研究

王锋，宋波

一类带切换的随机SIRS模型的稳定性研究

王锋1，宋波2

（1. 萍乡学院 工程与管理学院；2. 萍乡学院 初等教育学院，江西 萍乡 337000）

SIRS模型是经典的传染病模型之一。文章利用随机微分方程理论研究了一类带切换的随机SIRS模型的稳定性。结果表明，在一定的条件下，所建立的模型是随机渐近稳定的，这一结果可以用数值例子来验证。

随机SIRS模型；机制切换；全局正解；稳定性

引言

传染病是人类生存发展的重大威胁之一，当它发生并流行时，会给经济和人们的生活产生极其严重的危害。因此，建立传染病传播机制模型并对其研究，对于掌握疾病传播规律和控制疾病有重要的作用。SIR模型是一类经典的模型，它将群体分为3类：易受感染者（Susceptible）、感染者（Infected）和恢复者（Recovered），并假设感染者经过治愈恢复后不再具有重新感染的可能性。这类传染病有天花和水痘等。很多学者研究了这类模型的性质，见文献[1~2]。

在实际生活中环境不是一成不变的，它在时刻发生着变化，例如夏季冬季等季节的变化、温度、湿度的变化等。这些变化都会使得模型中的参数发生改变，而这种改变不能通过上述Brown运动这类连续的随机干扰来刻画，但能通过有限状态空间的连续时间Markov链来表示。因此，带Markov切换的SIRS模型获得了越来越多的关注[4-7]。Li等[6]研究了传播率由半马氏过程驱动的SIRS模型的动力学行为和遍历性。Bao等[7]研究了系数受状态依赖的Markov链调制的SIRS模型的持久、灭绝性。关于带切换的随机微分方程的系统知识和各种性质，可见文献[8]。

虽然研究带Markov切换的传染病模型较多，但是大多从疾病的持久灭绝性等动力学行为来研究，关于稳定性的研究则较少。本文研究具有一般发生率函数、带Markov切换的随机SIRS模型的稳定性，其形式如下：

求得。

1 基础知识

对于一个方程，首先考虑的是方程是否有解，解的范围能不能估计，下面的引理将研究这些问题。

将式（1）中三个方程相加起来，得到式子：

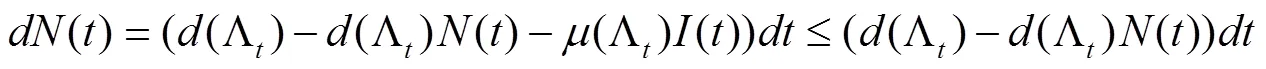
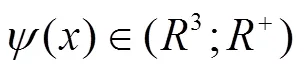
2 模型的稳定性

在本节我们将研究模型（1）的随机渐近稳定性。

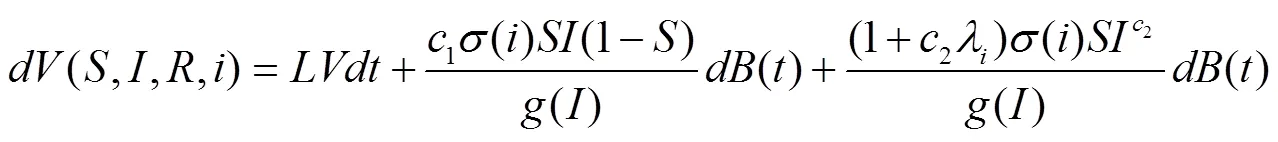
其中

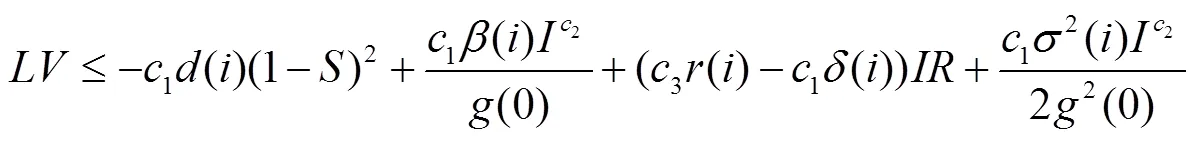
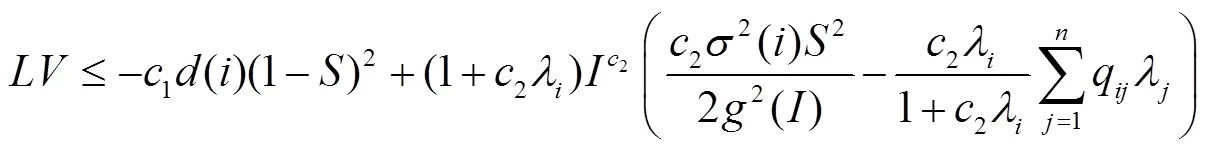
因此，

。（7）

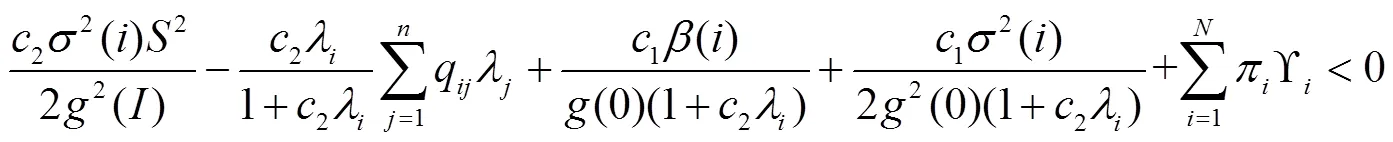
3 数值例子

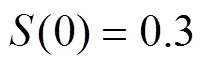
图1 例1中参数且模型（1）时N(t)的轨迹

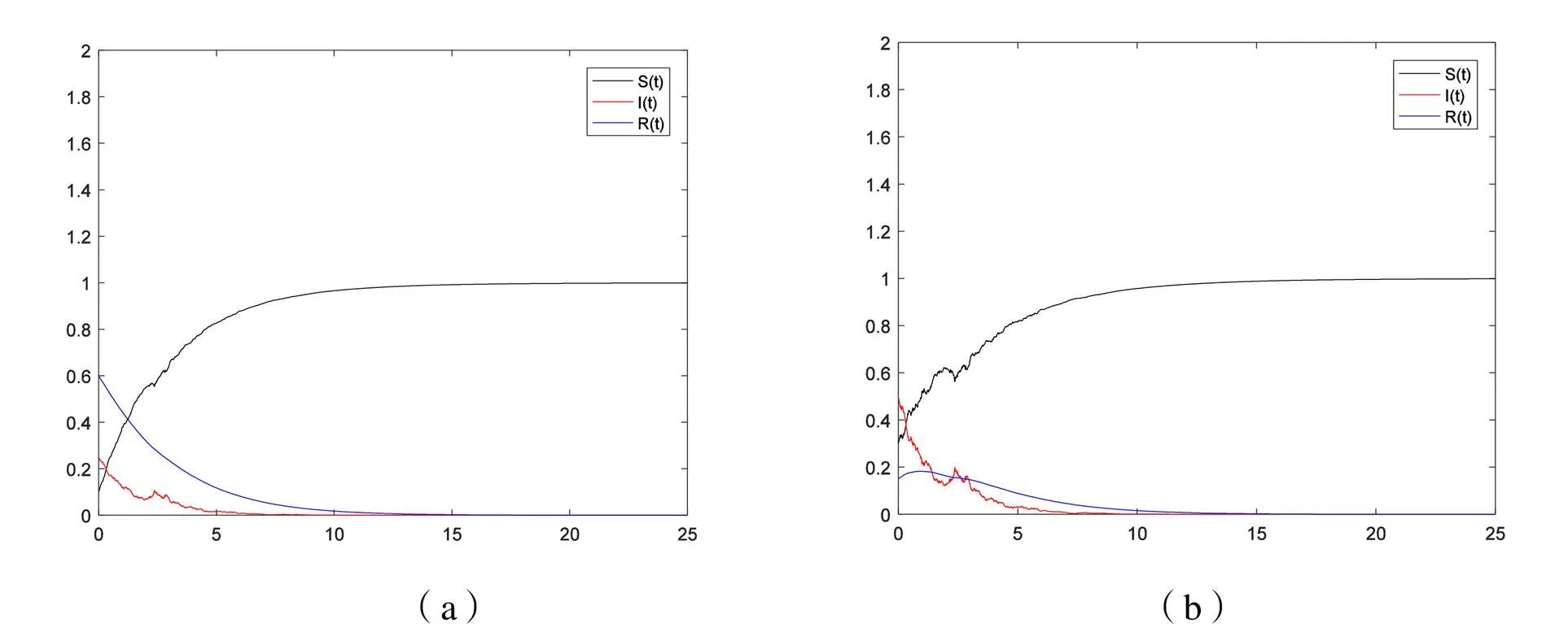
图2 例1参数下模型（1）时在不同初始值的轨迹

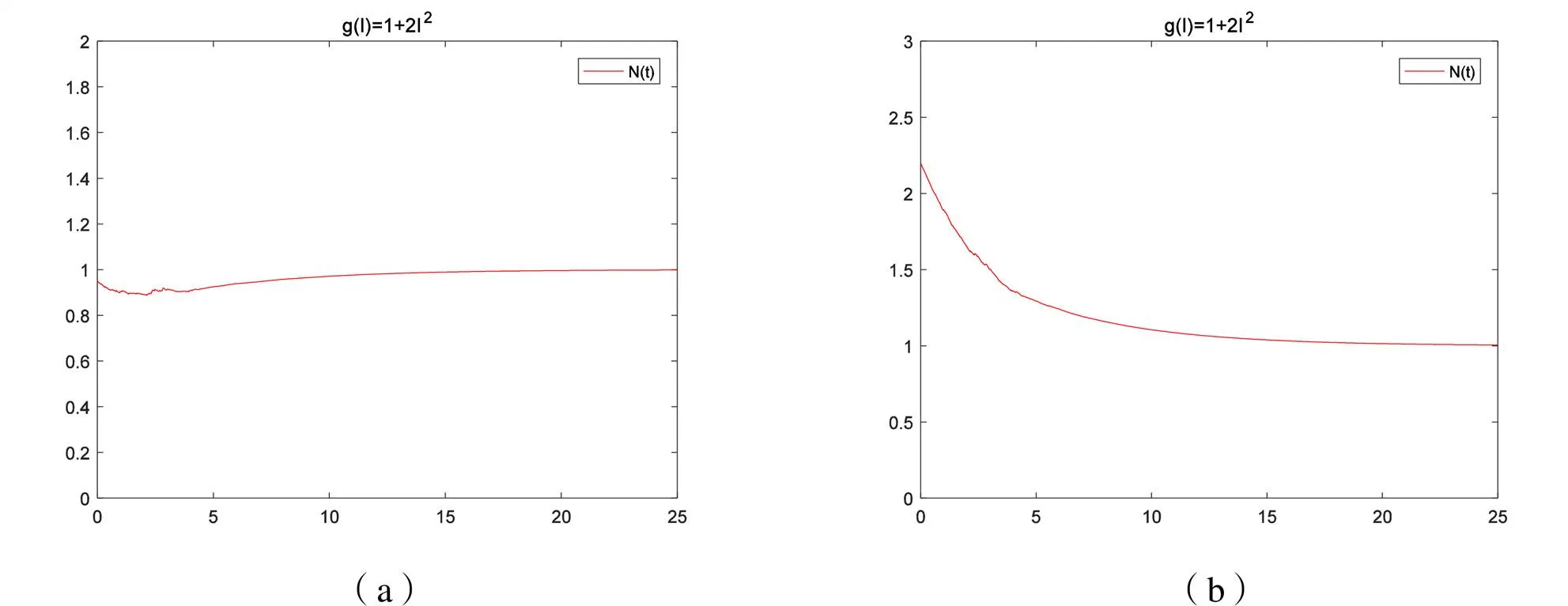
图3 例2中参数且模型（1）时N(t)的轨迹

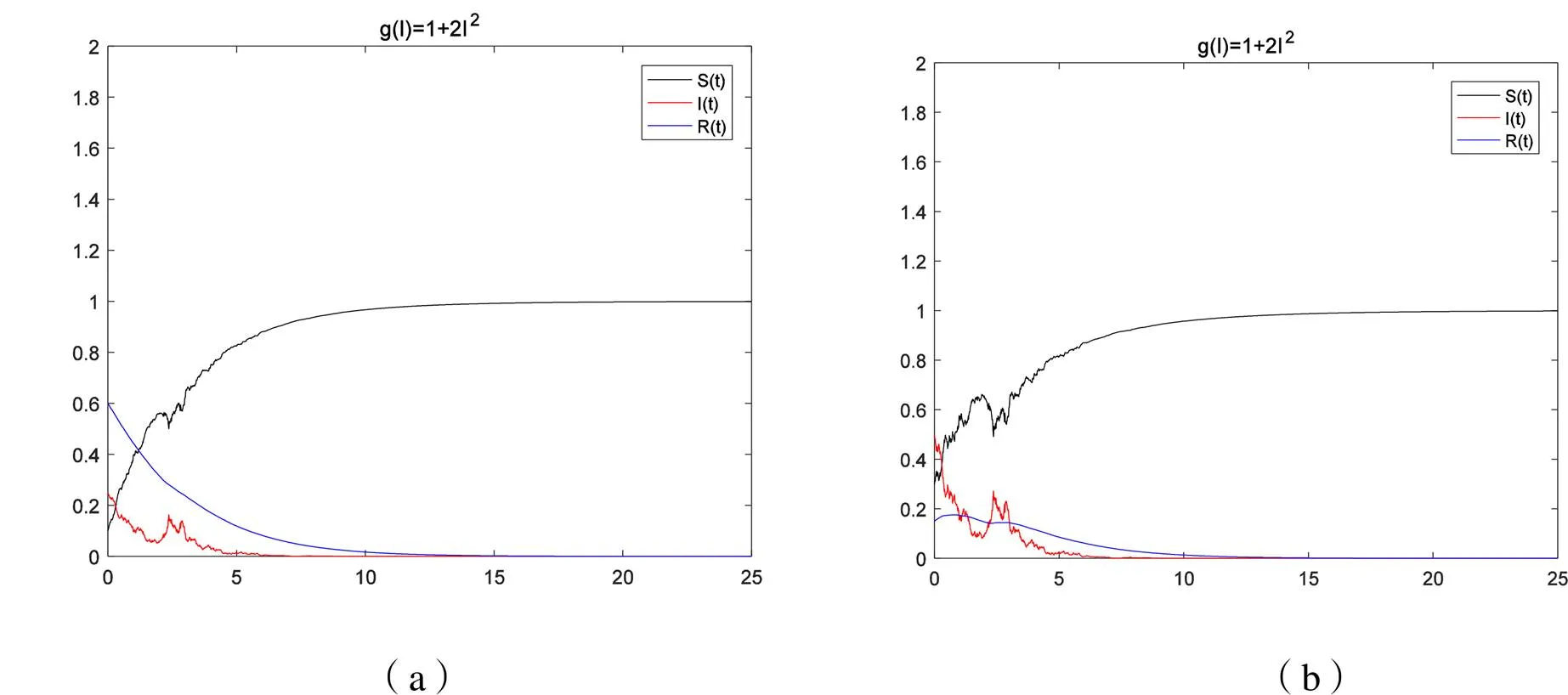
图4 例2参数下模型（1）时在不同初始值的轨迹

[1] E. Tornatore, S.M. Buccellato, P. Vetro. Stability of a stochastic SIR system[J]. Physica A, 2005, 354: 111~126.

[2] N.H.Du. Long-time behavior of an SIR model with perturbed disease transmission coefficient[J], Discrete Contin. Dyn. Syst. Ser. B, 2016, 21(10): 3429~3440.

[3] Y.L. Cai, Y. K.. A stochastic SIRS epidemic model with infectious force under intervention strategies[J]. J. Differential. Equations, 2015, 259: 7463~7502.

[4] D. Li, S. Liu, J. Cui. Threshold dynamics and ergodicity of an SIRS epidemic model with Markovian switching[J]. J. Differential. Equations, 2017, 263(12): 8873–8915.

[5] 王锋. Markov随机环境中随机SIRS模型的灭绝性研究[J]. 萍乡学院学报, 2019, 36（6）: 1~5.

[6] D. Li, S. Liu, J. Cui. Threshold dynamics and ergodicity of an SIRS epidemic model with semi-Markov switching[J]. J. Differential Equations, 2019, 266: 3973~4017.

[7] J.H. Bao, J.H. Shao. Asymptotic Behavior of SIRS Models in State-dependent Random Environments[J]. Nonlinear Anal. Hybrid Syst., 2020, 38 : 100914, 18 pp.

[8] X.R. Mao, C.G. Yuan. Stochastic Differential Equations with Markovian Switching[M]. London: Imperial College Press, 2006.

[9] R.Z. Khasminskii, C. Zhu, G. Yin. Stability of regime-switching diffusions[J]. Stoch. Proc. Appl., 2007, 117: 1037~1051.

〔责任编校：范延琛〕

Research on the Stability of a Stochastic SIRS Model with Switching

WANG Feng1, SONG Bo2

(1. School of Management and Engineering, Pingxiang University; 2. School of Primary Education, Pingxiang Jiangxi 337000, China)

SIRS model is one of the classical epidemic models. In the paper, the stability of a class of stochastic SIRS model with switching is studied by making use of the theory of stochastic differential equations. The results show that the model is stochastically asymptotically stable under certain conditions. Finally, some numerical examples are presented to verify the results.

stochastic SIRS model; Markovian switching; global positive solution; stability

2020-06-24

江西省教育厅科学技术研究项目（GJJ191145）；萍乡学院青年科研基金项目（2018D0224）

王锋（1987—），男，江西九江人，讲师，硕士，研究方向：随机微分方程及其应用。

O211.6；O29

A

2095-9249（2020）03-0007-06