纠缠光子源的性能模型与实验实现

王冬阳，吴俊杰，刘英文，杨学军

(国防科技大学计算机学院，湖南 长沙 410073)

1 引言

量子计算[1]是高性能计算的前沿研究方向。相对于经典计算与经典比特，量子计算以量子比特为基本单位；实验上，常将量子比特编码在某一物理体系上，通过对该物理体系状态的操控，完成计算过程。量子计算因其超强的计算能力，在许多科研领域有着显著的应用，如大数质因子分解[2 - 4]、线性方程组算法[5,6]和量子机器学习[7,8]等。但是，由于实验技术的限制，目前量子计算的物理实现仍处于初级阶段，核心原因是受限于可操控的量子比特的数目。

光量子计算是研究量子计算的一条重要途径。目前实现量子计算的物理体系包括光子[9,10]、离子阱[11]、超导[12]、原子[13]、量子电动力学腔[14]和核磁共振[15]等，而光量子计算以光子来实现量子比特的编码，通过光学元器件来操控并测量量子比特的状态，从而实现量子计算的过程。相对于其它的物理系统，光量子系统的优势在于可以快速地传播，相干时间长，性质稳定，不易受外界干扰，并且操控十分方便，因此是量子计算研究中的一个重要方向。

一套完整的光量子计算装置分为纠缠光子源(光量子比特)的制备、操控和探测3个部分。纠缠光子源是光量子计算研究中最重要的方面，所产生的光量子比特的性能直接影响了光量子计算装置的计算能力与效果。此外，通过光子与其它微观粒子的相互作用，可以实现混合物理体系的量子计算。因此，纠缠光子源的制备对于光量子计算和量子计算具有重要的意义。

光量子比特用来编码的状态种类包括偏振、路径、频率、动量和时间等，而偏振是用来编码光量子比特的一个主要自由度。目前偏振编码的纠缠双光子源主要以Kwiat等人[16,17]于1995年和1999年提出的自发参量下转换过程SPDC(Spontaneous Parametric Down Conversion)的方法为主。而纠缠多光子的产生以若干对纠缠双光子为基础，通过干涉的方式将其纠缠在一起而实现[18 - 22]。纠缠双光子的质量直接决定了纠缠多光子的质量。

衡量纠缠光子源的2个关键指标是纯度和亮度，前者描述了所产生光子的纠缠质量，而后者描述了其产生效率。影响纯度的一个因素是退相干现象，指的是所产生光子的各个叠加部分不再具有干涉的效果，从而使得各个部分的相干叠加性被破坏，影响纠缠性质。实验中与退相干相关的一个指标是纯度，退相干越严重，纯度越低。当退相干达到一定程度时，所产生的光子之间的纠缠作用就会被破坏。亮度反映的是最终接收到的纠缠光子的强度，如果所收集到的纠缠光子的亮度过低，将不利于光子的长距离、长时间操控。

如何提高纯度和亮度一直是纠缠光子源研究的一个重点和难点，代表工作包括通过空间补偿[23]和时间补偿[24]来提高纯度，以及通过研究晶体厚度与产率的关系，得到双光子亮度的最优解[25]。此外，纠缠光子的数目也在不断提高，已经达到了12光子纠缠的水平[22]。

但是，目前缺少关于纠缠光源完整的性能分析和理论模型，本文系统分析了基于I型SPDC的多光子纠缠光源的性能模型，设计实现了基于I型自发参量下转换的纠缠双光子源，为光量子计算的研究提供了理论和实验指导。具体贡献为：(1)研究纠缠双光子的纯度模型，得到提高纯度的方法；(2)研究纠缠双光子的亮度模型，得到提高亮度的合理聚焦参数；(3)研究纠缠多光子的产生模型，得到产生纠缠多光子需要满足的条件；(4)根据上述理论分析，在实验上产生了高纯度、高亮度的纠缠双光子。

本文结构如下所示：第2节简述利用I型SPDC过程产生纠缠光子的原理；第3节理论分析影响纠缠光子纯度和亮度的因素，以及从纠缠双光子到纠缠多光子的干涉过程；第4节利用第3节的理论分析，通过实验产生了高品质的纠缠双光子；第5节对工作进行总结与展望。

2 纠缠光子源的原理与结构

根据量子光学理论，通常激光器输出的光处于相干态，而用于光量子计算的光子源需要输出近似确定数目的粒子数量子态。SPDC过程是实现这2种量子态转换的重要方法。本节将介绍利用I型SPDC过程产生纠缠双光子与多光子的原理，以及衡量纠缠源质量的2个指标——纯度和亮度。

图1是利用I型SPDC过程产生偏振纠缠双光子的过程。当一束处于水平和垂直偏振的叠加态的激光(称为泵浦光)入射到2块特殊设计的非线性晶体上时，水平偏振的泵浦光会在第1块晶体上发生SPDC过程，产生垂直偏振的光子对，而垂直偏振的泵浦光会在第2块晶体上产生水平偏振的光子对。当泵浦光处于水平和垂直偏振的叠加态时，所产生的光子对为2个同时垂直与同时水平的叠加态，当这2种情况无法区分时，就形成了偏振纠缠。目前实验中主要采用偏硼酸钡(BBO)作为非线性晶体。

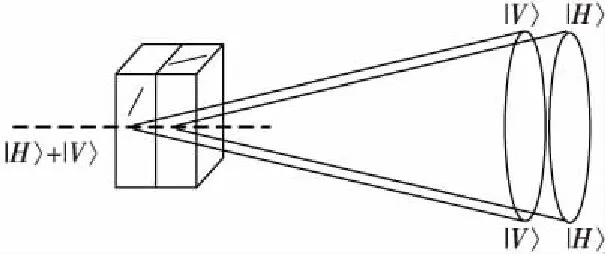
Figure 1 Generating two entangled photons using type-I SPDC process. A pump photon is converted into a pair of daughter photons at the center of the crystal, which form a circle spatially, |H〉 and |V〉 represent states of horizontal and vertical polarizations 图1 利用I型SPDC过程产生纠缠双光子泵浦光会在晶体处发生转换，产生一对转换光子，而转换光子在空间中的分布为一个圆环。|H〉和|V〉分别代表水平和垂直偏振状态

SPDC过程的发生需要满足的2个条件就是动量守恒(不需要严格守恒)和能量守恒。假设泵浦光子的频率和动量分别为ωp和kp,2个转换光子的频率为ωi、ki以及ωs、ks，那么能量守恒要求为：

ωp=ωi+ωs

(1)

定义动量差Δk=kp-ki-ks，根据非线性光学的理论，所产生的双光子的强度正比于sinc2(ΔkL)，其中L是晶体对应的厚度，sinc(x)≡sin(x)/x。当Δk=0时，所产生的双光子的强度最大。

由于2种下转换的过程发生在2个晶体中，因此|HH〉和|VV〉 2种情况在时间上存在一定的可区分性，这会使得两者不再是量子叠加的状态，而是处于部分的经典混合。纯度p定义为两者处于量子叠加的比例，p=1对应着完全的量子叠加，p=0对应着完全的经典混合。只有量子叠加的部分会存在纠缠性质，因此纯度p直接决定了纠缠的强弱。第3.1节将从理论上分析影响纯度p的因素，以及如何提高纯度p。

纠缠光子源的亮度指的是在单位时间内、单位泵浦光的功率下最终收集到的纠缠光子的数目，和泵浦光的聚焦参数有关。在实验中，为了提高SPDC的转化效率，需要利用透镜将泵浦光聚焦在晶体处，以达到集中能量的目的。如果聚焦的束腰过小，会使得转换光在远处的空间发散过快，不利于远距离收集；而如果聚焦的束腰过大，会导致泵浦光在晶体处的能量发散，使得光子的转换效率过低。3.2节将理论分析泵浦光束腰大小和最终亮度的关系，以及如何得到最优的亮度值。

纠缠多光子的产生，以纠缠双光子为基础，通过干涉过程完成，如图2所示。图中的PBS为偏振分束器，偏振分束器会反射垂直偏振的光子，透射水平偏振的光子。当2对纠缠双光子各取出一个输入到偏振分束器上后，并在2个输出端各探测到1个光子时，2个光子要么同时被透射(都处于水平偏振)，要么同时被反射(都处于垂直偏振)。而此时这4个光子的状态要么同时处于水平偏振，要么同时处于垂直偏振，当满足一定条件使得这2种情况无法区分时，这4个光子就形成了偏振纠缠。对于更多光子数的纠缠原理也是类似的。

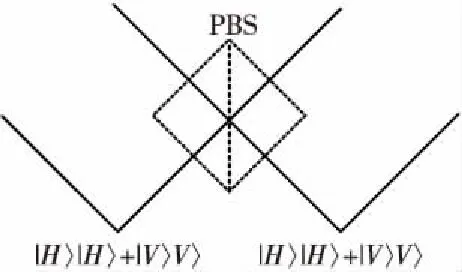
Figure 2 Generating four entangled photons using the interference of two pairs of entangled photons图2 利用干涉过程由2对纠缠双光子产生纠缠4光子

由于动量守恒和能量守恒，SPDC过程所产生的双光子在频率和动量上都是高度关联的，而这样的关联会破坏上述2种情况的不可区分性。3.3节将理论分析影响这种不可区分性的因素，得出产生多光子纠缠的条件。

3 纠缠光子源的性能模型

3.1 纠缠双光子的纯度模型

影响纠缠双光子纯度的因素主要包括时间可区分性和空间可区分性。目前大部分实验采用单模光纤收集光子，所以时间可区分性为主要因素。

本节将通过计算产生的|H〉|H〉和|V〉|V〉 2部分对应的波函数和时间的依赖关系，得到时间可区分性对于纠缠双光子纯度的影响。由于 2部分对应的均为I型SPDC过程(泵浦光为e光，2个转换光子为o光)，因此本文只计算第1块晶体产生光子的波函数。

根据非线性光学的理论，所产生的双光子波函数为:

fp(ωp)fs(ωs)fi(ωi)e-i(ωsτs+ωiτi)

(2)

其中,τ是转换光子从产生到被探测到的时间，f(ω)是泵浦光的频率包络函数和滤波片的滤波函数，下标p,s和i分别代表泵浦光和2个转换光子的函数(后面的下标含义相同)，Δk和L分别是之前定义的动量之差(这里只考虑传播方向上的动量，而默认横向的动量之差为0，此时动量可以看成是标量)和晶体的厚度。

为了计算波函数，需要计算各个动量以及Δk与频率的关系。假设泵浦光和转换光子的频率分别为ωp=Ωp+υp，ωs/i=Ωp/2+υs/i，而由能量守恒:

υp=υs+υi

(3)

根据动量和频率的关系，将各个动量值在各自的中心频率处进行泰勒展开，然后得到:

(4)

(5)

其中,σ是滤波片的带宽，σp是泵浦光的带宽，D+和D″分别为群速度色散和群速度失配项,υ-≡υs-υi。第2块晶体产生的双光子的波函数为Ψ(τ++Δτ,τ-)，Δτ为收集到的|HH〉和|VV〉光子的时间差。

结合一套具体实验的参数，泵浦光和转换光子的中心波长分别为405 nm和810 nm，非线性晶体选BBO晶体，DL值设为400 fs，本文做出了不同的σp以及σ下的双光子波函数的图像，如图3所示。

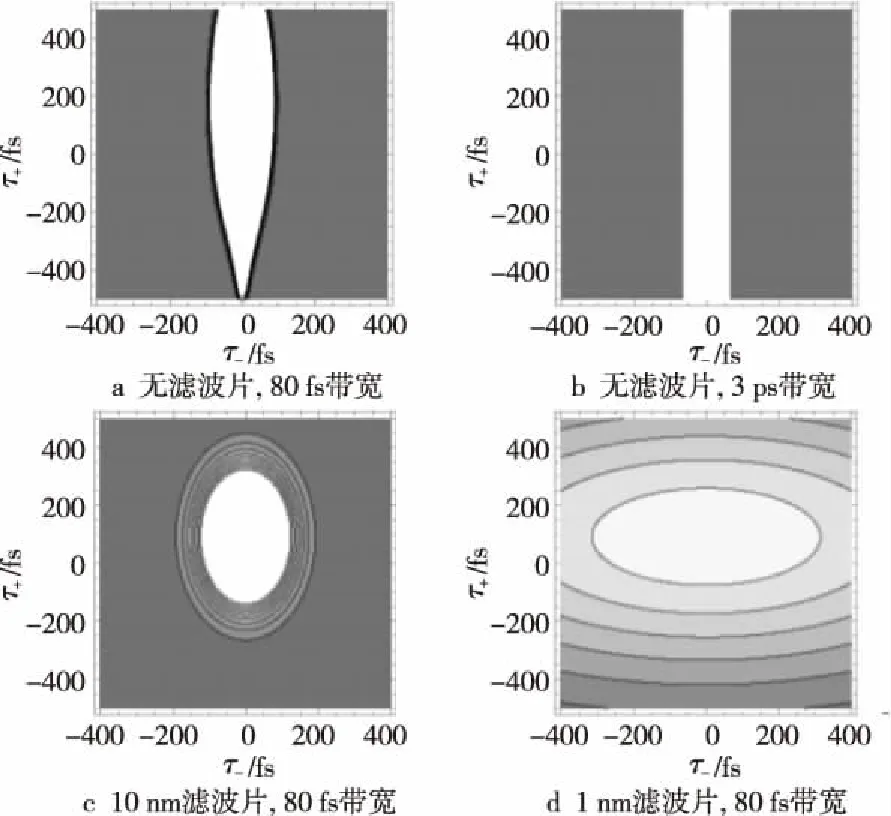
Figure 3 Calculated two-photon wavefunction Ψ(τ+,τ-) with different bandwiths of the filters and pump lights图3 计算出的双光子波函数Ψ(τ+,τ-)在不同滤波片带宽以及泵浦光时间带宽的情况

图3中横坐标为τ-，纵坐标为τ+，单位为fs。从图3中可以看出,I型SPDC过程产生的双光子在τ-方向是对称的，但是一般情况下，在τ+方向上是不对称的，这与II型过程产生的光子是相反的。而Ψ(τ++Δτ,τ-)的波函数图像对应于图中Ψ(τ+,τ-)的波函数在纵轴上平移Δτ。对于图3a，在没有滤波且泵浦光时间带宽较窄时,|VV〉和|HH〉重叠区域较少，即可区分性很大，这导致纯度很低；当泵浦光的时间带宽为3 ps时，对于图3b，此时泵浦光接近于在时间上连续的激光，此时2种波函数完全重叠，纯度较高；对于时间带宽较窄的泵浦光，对于图3c和图3d，当滤波的带宽变窄时，2种波函数重叠区域增加，纯度提高。

因此，基于纠缠双光子的纯度模型，本文得出以下结论：如果想要在实验中得到纯度较高的双光子，需要使用连续激光作为泵浦光，或者使用脉冲激光配合窄带滤波片使用。此外，对于飞秒激光器，当Δτ值过大时，还需要利用补偿的方法减小Δτ的值，提高2种波函数的重叠区域，从而提高纯度。

3.2 纠缠双光子的亮度模型

影响纠缠双光子亮度的因素包括晶体材料、模式匹配、泵浦光性质和元器件损耗等，而当实验器材固定时，泵浦光和转换光子的模式和收集模式的匹配是最重要的因素。

本节将计算双光子波函数和泵浦光束腰大小Wp以及收集转换光子所对应传播模式的束腰大小Wf的关系，得到使双光子亮度达到最大的Wp的最优值。

为了同时考虑泵浦光子和转换光子的空间高斯分布，根据相互作用绘景下的一阶微扰理论，将SPDC过程的双光子态表示为:

(6)

其中,i是虚数单位，ħ是约化普朗克常数，t表示时间，HI是系统的相互作用哈密顿量，可以表示为:

(7)

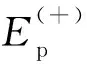
为了便于计算，本文选取了图4的坐标系[25]，其中包括泵浦光和2个转换共3个坐标系，考虑泵浦光为单色，并且因为最终用单模光纤收集转换光子，本文忽略转换光子电场的横向动量分布，只考虑其频率对于纵向动量的影响。

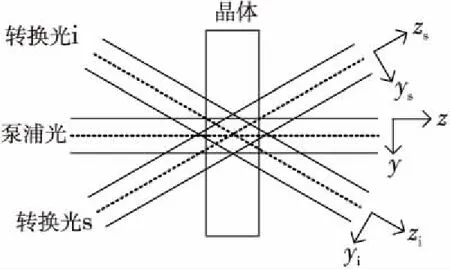
Figure 4 Coordinate system in SPDC process图4 SPDC过程对应的坐标系

在这样的近似下，各个电场的部分表示为:

(8)

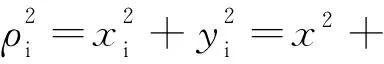
(9)

利用这样的坐标变换关系，本文得到了最终的哈密顿量:

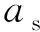
(10)

其中被积函数表示为:

i(kpz-(ks+ki) cosθz))

(11)

其中，函数的实部表示真实的物理量，后文类似。

利用和3.1节一样的泰勒展开，经过计算得到Iz的具体形式和系统的波函数|Ψ〉。系统最终的双光子产率可以估计为:

R=〈Ψ|Ψ〉∝γ2(2γ2+1)-2

(12)

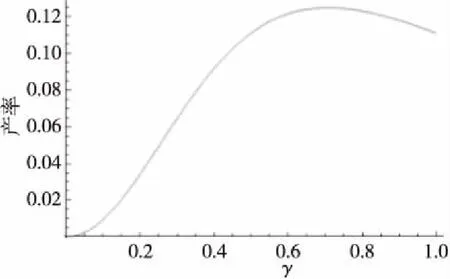
Figure 5 Variation of two photons’ generation rate with γ图5 双光子产率随着γ的变化

3.3 纠缠多光子的产生模型

目前纠缠多光子主要是通过来自不同的纠缠光子对的光子之间的干涉[26]产生的。本节从来自2个光子对的双光子HOM(Hong Ou Mandel)干涉[27]出发，指出通过干涉的方式得到多光子纠缠所需要满足的条件。

HOM干涉是一个著名的双光子干涉实验。考虑2个光子分别入射到同一个分束器的2侧，它们都有一半的几率被反射，一半的几率被透射。而当2个光子完全不可区分时，它们要么同时被反射，要么同时被透射，也就是说无法在2个探测器同时接收到光子。

图6是来自2个光子对的双光子HOM干涉装置，其中BS是光束分束器。相比于普通的HOM干涉，其发生干涉的2光子来自2个SPDC过程产生的光子，此时由于发生干涉的2光子(记为i光子)的可区分性有可能被对应的s光子泄露，因此需要更为严格的限定条件。

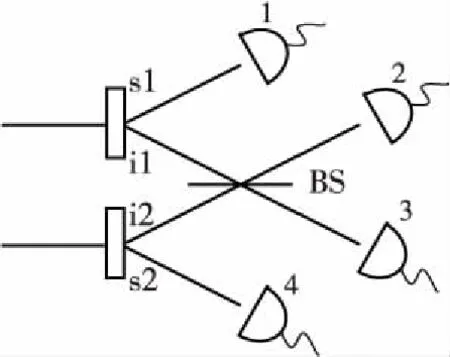
Figure 6 HOM interference of two photons from different pairs图6 来自2个光子对的双光子HOM干涉

计算方法是类似的。本文首先考虑在4个探测器端的电场和转换得到的4光子对应的电场之间的关系：

(13)

其中，T和R分别代表透射率和反射率，对于一个对称的分束器，取值均为0.5。τ代表2个s光子从产生到被探测的时间，δτ代表干涉的2个i光子到达分束器的时间差，下标对应的光子参照图6。

通过电场可以计算出对应的4光子波函数，不失一般性，本文取脉冲型泵浦光、完美相位匹配，以及高斯型滤波片，暂时忽略泵浦光的横向分布，进而得到4光子符合的概率为:

e-i(vi2,vi1)δτf(vs1,vi2)f(vs2,vi1)|2dvs1dvi1dvs2dvi2

(14)

其中本文取转换光子的频率为:

ωs=ω0+vs,

ωi=ω0+vi

(15)

对应的联合谱分布函数为高斯型泵浦光的谱包络函数和滤波片的滤波函数的乘积。上述积分区域应该是符合计数的时间窗口，若时间窗口远远大于光子的相干时间，积分区域可以近似为无穷。

通过计算上述积分值，本文得到最终的4光子符合概率为:

(16)

当时间差δτ=0时，符合概率值达到最小，也对应于发生干涉的2光子的可区分性最弱。当采取滤波的带宽σf远远小于泵浦光的带宽σp时，

(17)

即2光子接近于不可区分的状态。此时对应于产生光子的相干时间远远大于脉冲泵浦光的脉冲持续时间。

当σp=0时，对应于单频连续激光器的情况，此时完全没有对比度。所以，只能取时间窗口远远小于单光子的相干时间，在这样的情况下，之前的4重积分限不能取为无穷，因此可以利用积分中心的函数值来计算，从而得到:

(18)

同样可以达到不可区分的效果。

本文以此为基础，进一步分析目前利用干涉方式由纠缠双光子产生纠缠4光子的实验装置，计算过程是一样的，只是要将偏振的自由度考虑进去。假设在偏振检验中，每一个探测器端口前放置的偏振片的设置为cosθ|H〉+sinθ|V〉，对应于之前分析的可区分和不可区分2种情况下，4光子的符合概率P(0)分别对应着4光子纠缠态的纯度为1以及为0 2种情况。

因此，基于纠缠多光子的产生模型，本文得出以下结论：如果想要利用干涉的方式由纠缠双光子得到纠缠多光子，就需要满足达到此种类型的HOM干涉的条件。对于连续泵浦光，条件是光子相干时间大于时间窗口；对于脉冲泵浦光，条件是光子相干时间大于脉冲的持续时间，而放宽对于时间窗口的要求。

4 I型SPDC纠缠双光子源实验

结合之前的理论计算，本文在实验中利用连续激光器产生了高纯度的纠缠双光子[28]，并且测量了双光子的亮度和泵浦光聚焦的束腰大小之间的关系。

4.1 实验装置

图7为纠缠双光子产生装置,其中，LP是长通滤波片，IF是带通滤波片，Pol是偏振片，APD是雪崩光电二极管探测器。基于之前的理论分析，本文设计了如图7所示的纠缠双光子实验装置图。本文采用连续激光器作为泵浦光，波长为405 nm，功率为80 mw；使用的非线性晶体为2块粘合的BBO晶体，厚度各为0.6 mm。由于此款激光器的泵浦光频率带宽较窄，因此本文采取的滤波装置为中心波长为810 nm，半高全宽为10 nm的滤波片。根据3.1节的理论计算，这种实验参数可以消除|HH〉和|VV〉的可区分性，达到较高的纯度。

Figure 7 Experiment setup of generating two entangled photons图7 纠缠双光子产生装置

本文采用透镜对泵浦光进行聚焦。产生的光子先由偏振片进行偏振检验，然后由光纤耦合器耦合进光纤，再由雪崩光电二极管探测器将光信号转换成电信号，最后由符合计数系统[29]对电信号进行探测。为了减少光子的损耗，本文实验中的相应镜片都做了相应波长的增透镀膜。在晶体之前，需要对泵浦光的偏振态进行初始化。根据相关理论，由2个四分之一波片和半波片组成的三明治结构，可以制备光子的任意偏振态[30]。

实验通过2个光子的偏振关联来检验所产生的双光子的纯度。根据量子力学的理论，假设所产生的双光子的纯度，即|HH〉和|VV〉量子叠加的比例为p，那么当固定一个探测端口前偏振片的角度为45°偏振，然后观察2光子计数随着另一个探测端口前的偏振片角度的变化，所获得曲线的对比度也为p。

4.2 实验结果与分析

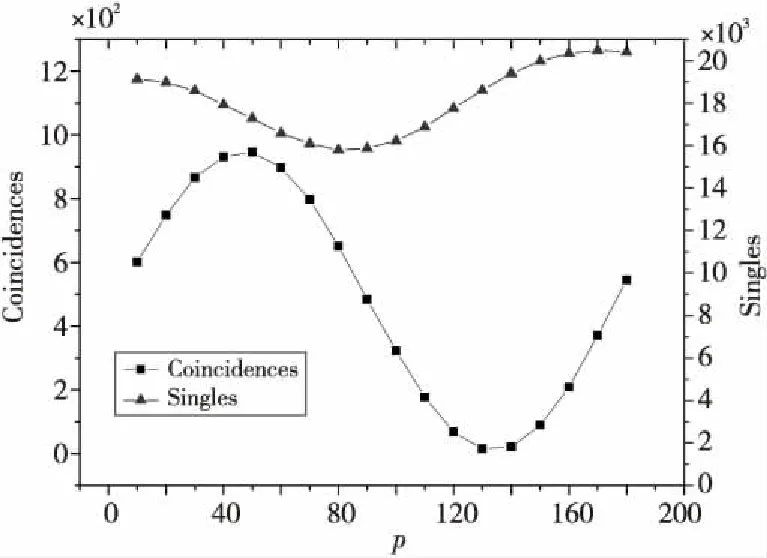
Figure 8 Measured correlation curve of the two photons’ polarizations图8 测得的双光子的偏振关联曲线

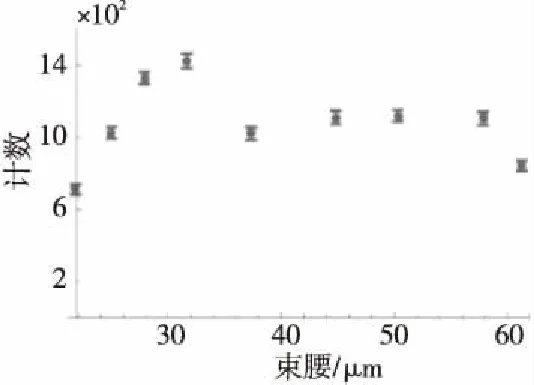
Figure 9 Measured variation of the two photons’ count with the waist of the pump light图9 测得的双光子计数随着泵浦光束腰大小变化

5 结束语

光量子计算是实现量子计算的一个重要途径，而在光量子计算中，纠缠多光子的产生是难度最大，也是最关键的一部分。本文研究了由SPDC过程产生纠缠光子的理论模型，得出以下结论：(1)为了得到高纯度的纠缠光子，需要使用连续泵浦光，或者利用飞秒泵浦光配合窄带滤波片使用。此外，对于飞秒泵浦光来说，当2块晶体对应的时间差过大时，还需要利用时间补偿晶体缩减时间差，进而提高纯度。(2)为了得到高亮度的纠缠光子，需要将泵浦光的束腰和收集模式相匹配。(3)为了利用纠缠双光子得到纠缠多光子，对于连续泵浦光需要使光子相干时间大于时间窗口；对于脉冲泵浦光，需要使光子相干时间大于脉冲的持续时间。

基于理论分析，本文通过实验产生了纯度为97.25%的纠缠双光子，同时测量了双光子亮度与泵浦光束腰大小的关系，结果符合理论分析的结果。由于受到实验条件的限制，针对第3.3节理论研究的干涉与多光子纠缠的内容，本文没有进行实验验证，这一点将在后续研究中完成。