GPU上典型存储器难散列函数的优化

陈 虎，韩建国

(1.华南理工大学软件学院，广东 广州 510006;2.广东省科技基础条件平台中心,广东 广州 510006)

1 引言

在口令安全机制中，往往基于一般散列函数构造特定的口令散列函数。在设置口令时，口令验证方计算并存储用户口令明文对应的口令散列函数值(密文)，从而避免口令明文的泄露。在验证口令时，口令验证方计算用户输入口令对应的口令散列函数值并与存储的密文进行对比。在恢复口令时，可以并行计算多个口令明文的散列值，并与待猜测的密文比较。因此，口令散列函数的计算性能成为口令攻防两方面的关键性问题。可以使用MD5[1]、SHA1[2]等简单散列函数作为口令散列函数，其计算过程较为简单，但难以抵抗较大规模的口令攻击。也可以使用PBKDF2[3]等构造口令散列函数，其通过多次迭代简单散列函数以增加计算量，但是此类计算密集型的散列函数易于在FPGA、ASIC等专用硬件上[4,5]并行计算多条口令明文的散列函数实例，具有较高的性能，对口令安全构成潜在威胁。

存储器难散列函数(Memory-Hard Hash Functions)[6]具备抗ASIC攻击的能力，有望成为新型的口令散列函数。这类散列函数在执行过程中需要较大的存储器容量，而且计算和访存的比例相近。这使得ASIC上实现该类函数面临困难：如果将散列函数计算所需要的存储器都放置在ASIC芯片上，将占用大量的晶体管，从而降低芯片的计算能力；如果采用片外存储器存储，芯片的存储器访问带宽可能会成为系统瓶颈，而且存储器访问的功耗依然与传统的CPU/GPU系统相当[7]。

得益于强大的计算能力和完整的生态环境，高性能的通用GPU[8,9]是当前口令恢复的主要硬件平台。hashcat[10]、John the Ripper[11]等高效的口令猜测软件对传统的口令散列函数进行了深入的优化，具有很高的执行效率，但是在GPU上优化实现存储器难散列函数的方法还没有得到深入的研究。

本文主要研究利用GPU体系结构的特点提升存储器难散列函数计算吞吐率的方法。GPU的片上存储器容量非常有限，难以在片上存放这些散列函数所需要的存储空间。但是，GPU提供了很高的存储器访问带宽和较大容量的全局存储器，可以在全局存储器中存放存储器难散列函数所需要的内容。为了更有效地发挥GPU潜在的计算能力，本文一方面研究了存储器难散列函数的数据布局，以提升存储器的访问效率；另一方面利用GPU上多线程间寄存器交换数据的方法，使多个线程协作执行同一个散列函数实例，从而增加线程的数量，更好地隐蔽存储器的访问延迟，提升吞吐率。

本文以经典的存储器难散列函数Scrypt[12]为例说明了GPU上优化实现方法，并使用该方法优化实现了较为复杂的存储器难散列函数Argon2d[13]。与hashcat的实现方法相比，本文提出的优化方法使得Scrypt的性能提升了2.03倍。

本文第2节介绍存储器难散列函数和GPU体系结构的基本特点；第3节介绍对Scrypt的优化实现方法；第4节讨论Scrypt性能测试结果，并简要介绍Argon2d算法的性能，说明本文提出的方法可以优化多种存储器难散列函数；第5节总结了本文的工作。

2 相关工作

2.1 存储器难散列函数

存储器难散列函数的主要特征包括：(1)每个实例执行过程中需要占用较大容量的存储器，其存储器容量参数往往可以配置，从数百K字节到数G字节不等。从口令安全的实际应用场景看，其存储器容量往往介于数百K字节至数M字节。(2)可以分为独立型和依赖型2种。前者的存储访问地址序列固定，与输入的明文无关，具有较好的抗侧信道攻击能力，但由于地址序列固定，可以通过预先优化存储器布局获得较高的计算性能[14,15]。后者的存储器访问地址依赖于散列函数的输入明文，事先难以确定存储器访问的地址序列，这使得系统实现更为困难。(3)散列函数执行过程中计算和访存比例较为接近，在实现的过程中如果减少内存的使用量，则会显著增加计算量。这个特征使得在ASIC上使用较少的片上存储器压缩存储变得得不偿失。

典型的存储器难散列函数包括Scrypt、Argoon2、Lyra[16]和Ballon[17]等，其中Scrypt是出现较早的存储器难散列函数，目前已经成为RFC标准[18]。Argon2是2015年口令散列函数竞赛[19]的优胜者，包含依赖型和独立型2种类型：Argon2d和Argon2i。Argon2原理较为复杂，限于篇幅，本文仅介绍Scrypt的原理。

Scrypt的配置参数包括：CPU/存储器开销参数N、块大小r、并行度p和输出长度dkLen，输入包括口令pwd和盐salt。Scrypt的原理如图1所示，分为3个步骤：

(1)使用PBKDF2_HMAC_SHA256(pwd,salt,p×128r)生成p个128r字节的初始数据块，分别作为p个线程的输入B。

(2)p个线程使用ROMix算法分别填充p块容量为N×128r字节的存储器，并迭代得到128r字节的结果B′。

(3)对p个结果使用PBKDF2_HMAC_SHA256生成长度为dkLen位的散列函数值。

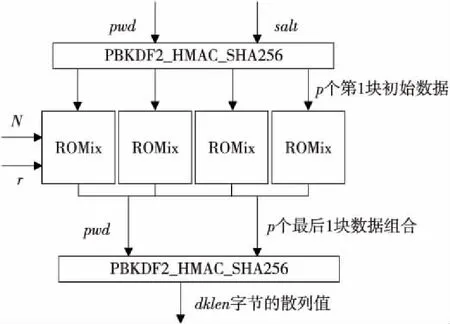
Figure 1 Structure of Scrypt图1 Scrypt结构

ROMix算法包含了N个128r字节块构成的数组V，其中第1块V0由PBKDF2_HMAC_SHA256()所产生的1个128r字节块B初始化。在第1阶段(第2～4行)中，Scrypt按照顺序依次使用BlockMix算法填充数组V，其中Vi仅仅依赖于Vi-1。在第2阶段(第5～7行)中，第6步的Integerify函数取X的最后64字节作为一个小端对齐的整数，并由此随机选择V中的一个块，在第7步中更新X。经过N次迭代后，得到128r字节的输出B′。ROMix算法依赖关系如图2所示，其中X0,…,XN-1对应算法1中第7步X在第i次循环时的值，节点之间的实线为必然的依赖关系，虚线为随机的依赖关系。

算法1ROMix算法

Input:B,r,N。

Output:B′。

1:X←B;//X为中间变量

2:forifrom 0 toN-1do

3:Vi←X;

4:X←BlockMix(X)

5：endfor

6:forifrom 0 toN-1do

7:j←Integerify(X) modN;

8:X←BlockMix(X^Vj);

9：endfor

10:B′ ←X;

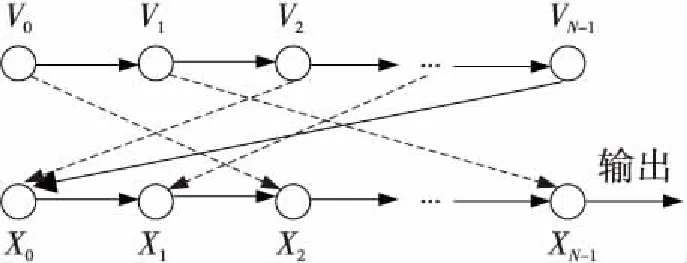
Figure 2 Dependency graph of ROMix图2 ROMix算法的数据依赖图

BlockMix算法由Salsa20/8散列函数派生得到，其输入和输出都是2r个64字节的数据块，如算法2所示。

算法2BlockMix算法

Input:2r个64字节的数据块B0…B2r-1。

Output:更新后的2r个64字节的数据块B′0…B′2r-1。

1:X←B2r-1；//X为中间变量

2:forifrom 0 to 2r-1do

3:T←X^Bi；//T为中间变量

4:X←salsa20/8(T);

5:Yi←X；//Yi(0≤i≤2r-1)为中间变量

6:endfor

7:B′←(Y0,Y2,…,Y2r-2,Y1,Y3,…,Y2r-1)

存储器难散列函数Scrypt具有以下特点[12]：

(1)在串行随机访问的计算机上，需要的存储空间为O(N)，计算次数T(N)=O(N)。

(2)在具有S*(N)=M(N)个处理器和S*(N)存储空间的并行随机访问计算机上，算法执行时间T*(N)=O(N2/M(N))，即SN(N)×T*(N)=O(N2)。

Scrypt的主要特点是计算次数和所需要的存储器容量成正比，且在并行计算机上其时空乘积为O(N2)，这使得它在并行计算机上的速度提升无法按照硬件资源的数量增加呈线性关系。

2.2 GPU体系结构特点

与CPU相比，GPU使用了更多的晶体管构造计算单元，片上存储器容量非常小。GPU中包含了多个流多处理器组SM(Stream Multiprocessors)，每个SM包含了多个计算单元、64～192 KB的共享存储器/Cache和大容量的寄存器文件。一个SM上可以同时并发运行多个轻量级线程，并且零开销实现线程切换。

NVIDIA公司的GPU采用了单指令多线程SIMT(Single Instruction Multiple Threads)[8]的并行方式，即多个线程执行相同的指令，但是使用不同的数据。SM调度的基本单位是由32个线程构成的warp，同一个warp的所有线程执行相同的指令。同一warp内的线程可以使用混洗指令直接交换数据，无需访存存储器，执行开销很小。一个warp执行高延迟的访存指令时，将会挂起直至访存指令结束。在此期间，执行算术逻辑指令的其他warp仍可以并发执行，可以在一定程度上隐藏内存访问的延迟。

GPU访问全局存储器的基本单位[20]是以128字节为单位的区段。一个warp的32个线程可以同时访问32个不同地址。如果这32个地址均处于一个区段内，一次全局存储器访问就可以满足这个访问请求。如果这32个地址分散在m个区段，则需要m次全局存储器访问，存储器访问效率降低为1/m。

3 GPU上Scrypt算法的优化

存储器难散列函数在执行过程中使用的内存容量较大，同时伴随着大量的访存操作。需要优化全局存储器的数据布局，提高存储器带宽的利用率。与此同时，口令恢复过程可以并行执行多个散列函数实例。如果一个GPU线程计算一个散列函数实例，由于受到显存大小的约束，GPU中线程数量受限，难以隐藏存储器访问带来的延迟。

本文采用多个线程协作计算一个散列函数实例的方法，使得在同样散列函数实例的情况下，具有更多的工作线程，更为有效地隐藏存储器访问延迟。

3.1 2种存储器布局

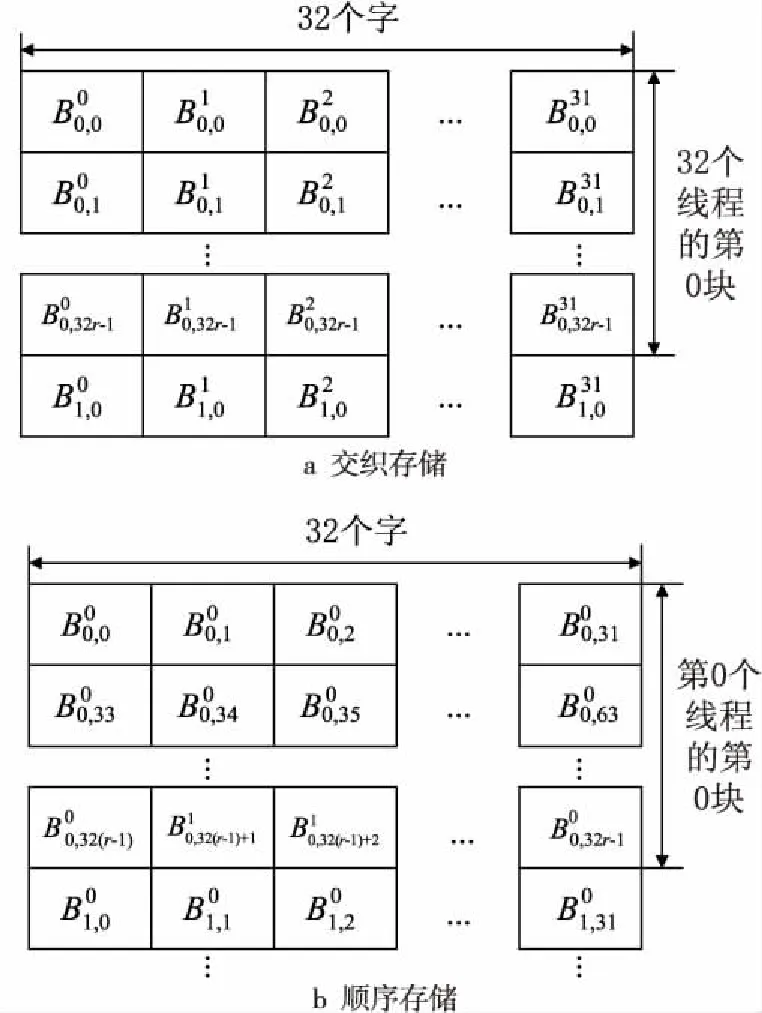
Figure 3 Two storage methods图3 2种存储方式

在交织存储方式中，每个warp交织存储32个线程的内容，即不同线程的相同位置的字连续存放。在顺序存储方式中，同一个线程对应数据连续存放，不同线程的存储区域不发生交叠。对于一个warp中第t个线程的第i个块的第j个字，交织存储的地址AI和顺序存储的地址AN的计算方法分别如式(1)和式(2)所示：

AI(t,i,j)=32×(32r×i+j)+t

(1)

AN=32r×N×t+32r×i+j

(2)

其中,0≤t≤31，0≤i≤N-1，0≤j≤32r-1。

交织存储方式中，一个warp中的32个线程同时计算32个Scrypt散列函数实例，且每个线程按照32位无符号整数的方式并行访问存储器。ROMix算法的第1阶段，32个线程发出的存储器访问地址处于一个128字节的区段中，GPU的带宽利用率为100%。但是，在第2阶段中，32个线程可能访问不同的块，导致32个地址处于不同的区段中。在最坏的情况下，所需要读取的数据分布于32个不同的区段，此时存储器带宽的利用率仅为1/32。

在顺序存储方式中，每个线程计算一个Scrypt实例且仅使用32位存储器访问时，存储器带宽利用率为1/32。为了避免这个问题，可以使用16字节的存储器访问。CUDA的程序设计指导[20]指出，如果warp中每个线程均访问16个字节存储器，则GPU产生4个存储器访问请求，且每个请求完成8个线程的存储器访问。如果这8个线程计算不同的实例，其地址将处于不同的区段，在Scrypt的2个阶段中存储器带宽的利用率均为1/8。

3.2 多线程协同计算

由于GPU的显存容量有限，在N较大的情况下，可以同时支持的Scrypt散列函数实例数受到限制，导致能并发计算的线程数有限，从而影响系统的吞吐率。为此，本文考虑4个线程协同计算1个散列函数的实例。

Scrypt的主要计算基于散列函数Salsa20/8[21]，其伪代码如下所示，其中R(d,s)表示对32位无符号整数d循环右移s位。

算法3Salsa20/8

{//b0…b15:16个32位的字输入

//x0,…,x15:16个中间变量

1:x0…x15←b0…b15;

2:forifrom 0 to 3do

3:x4^=R(x0+x12,7);x8^=R(x4+x0,9)；

4:x12^=R(x8+x4,13);x0^=R(x12+x8,18)；

5:x9^=R(x5+x1,7);x13^=R(x9+x5,9)；

6:x1^=R(x13+x9,13);x5^=R(x1+x13,18)；

7:x14^=R(x10+x6,7);x2^=R(x14+x10,9)；

8:x6^=R(x2+x14,13);x10^=R(x6+x2,18)；

9:x3^=R(x15+x11,7);x7^=R(x3+x15,9)；

10:x11^=R(x7+x3,13);x15^=R(x11+x7,18)；

11:x1^=R(x0+x3,7);x2^=R(x1+x0,9)；

12:x3^=R(x2+x1,13);x0^=R(x3+x2,18)；

13:x6^=R(x5+x4,7);x7^=R(x6+x5,9)；

14:x4^=R(x7+x6,13);x5^=R(x4+x7,18)；

15:x11^=R(x10+x9,7);x8^=R(x11+x10,9)；

16:x9^=R(x8+x11,13);x10^=R(x9+x8,18)；

17:x12^=R(x15+x14,7);x13^=R(x12+x15,9)；

18:x14^=R(x13+x12,13);x15^=R(x14+x13,18)；

19:endfor

20:forifrom 0 to 15do

}

上述函数可以分为2段：第1段是第3行到第10行，第2段是第11行到第18行。将16个中间变量划分为{x0,x4,x8,x12}，{x1,x5,x9,x13}，{x2,x6,x10,x14}和{x3,x7,x11,x15}4个集合。基于此数据划分，第1段的16个移位/加法操作可以按照下述计算次序由4个线程分4步并行完成：〈x4,x9,x14,x3〉，〈x8,x13,x2,x7〉，〈x12,x1,x6,x11〉，〈x0,x5,x10,x15〉。同理，第2段的计算过程中，4个线程使用的数据集合分别为{x0,x1,x2,x3}，{x4,x5,x6,x7}，{x8,x9,x10,x11}，{x12,x13,x14,x15}，并行计算次序为：〈x1,x6,x11,x12〉，〈x2,x7,x8,x13〉，〈x3,x4,x9,x14〉，〈x0,x5,x10,x15〉。由此可以看出，可以使用4个线程同时完成一个Salsa20/8散列函数的计算。需要设计中间变量x0, …,x15的存储布局和交换方法，使得每个线程分别包含4个局部变量，并行执行第1段操作，然后进行一次数据交换，再并行执行第2段操作。

在GPU中可以使用共享存储器或warp混洗函数实现同一个warp内多个线程间数据交换。共享存储器分为16个存储器体，如果1个warp中的16个线程同时访问不同体，可以达到共享存储器体的最大访问带宽。可以将协同计算同一个实例的4个不同线程的中间变量x0, …,x15分布到不同的存储器体上，并精心排布第2段计算的次序(如图4所示)，使得4个协作线程在整个Salsa20/8计算过程中不发生体冲突，但是这将引入比较复杂的地址计算。另外一种方法使用了NVIDIA公司特有的warp混洗函数实现同一个warp内的多个线程间快速数据交换。测试表明，使用warp混洗函数的性能稍高于使用共享存储器的性能，这可能是因为共享存储器地址计算的开销和较高的存储器访问延迟导致的。因此，本文在NIVIDIA公司的GPU上使用了混洗函数。在不支持warp混洗函数的其他类型GPU上可以考虑采用局部存储器的交换方法。

Figure 4 Layout of intermediate variables in Salsa20/8图4 Salsa20/8中间变量的存储布局

4 测试与分析

本节在GTX TITAN X上进行性能测试，其硬件参数如表1所示。测试主要包括3个方面：(1)在(N,p,r)=(1024,1,1)的参数配置下，比较交叉存储、单线程顺序存储和4线程顺序存储3种方法实现Scrypt的性能；(2)上述3种方法实现Argon2d的性能；(3)所需存储容量变化时，散列函数的性能。

在 (N,p,r)=(1024,1,1)情况下，3种不同方法实现Scrypt性能如表2所示，其中hashcat使用了单线程顺序存储方法。由表2可以看出，4线程顺序存储方法具有最高的性能，是hashcat实现方法的2.03倍。

Table 2 Scrypt performance of three different methods(N=1024, p=1, r=1)表2 3种不同方法的Scrypt性能(N=1024,p=1,r=1)

Argon2d也是一种典型的存储器难散列函数，其主要配置参数包括：并行度p，存储器容量m，迭代次数T。一个Argon2d实例所需要的存储容量为1204mp个字节。它在填充存储器阶段采用基于blake2b[22]的压缩函数。与Salsa20/8类似，该函数可以由4个线程并行实现，也可以使用本文所述的4线程顺序存储方法。表3给出了3种方法的性能比较，可以看出，4线程顺序存储方法的性能是交织存储方法性能的310%。

Table 3 Argon2d performance of three different methods(m=64, p=1, T=1)表3 3种不同方法的Argon2d性能(m=64,p=1,T=1)

当N=1024时，一个Scrypt散列函数的实例需要128 KB的全局存储器容量。在总容量为12 GB的显存中，约有8～9 GB存储器可供使用。在此配置下，4线程顺序存储方法可以使用的线程数为252K个，每个SM容纳2K个线程。

受到显存容量的限制，当N增加时，单个GPU上可以并行计算的实例数(线程数)也在不断下降，如表4和图5a所示。在Scrypt散列函数中，N增加一倍，计算和访存的数量也都相应增加一倍。在理想的情况下，N增加一倍，计算性能应降低一半。但是，实际性能降低的速度远远高于50%。例如，在N=2048时，计算性能仅为N=1024时性能的12.65%。发生这种情况的主要原因是GPU中对全局存储器访问的延迟高达200～400个周期，需要依赖大量计算密集型的线程隐藏存储器访问导致的延迟。但是，N(单个实例的内存使用量)增加时，可以并行计算的线程数随之减少，降低了对存储器访问的隐藏能力，导致系统资源利用率和吞吐率显著下降。

Table 4 Scrypt performance with different storage capacity (p=1, r=1)表4 Scrypt散列函数存储容量变化时的性能(p=1，r=1)

与Scrypt类似，在其他参数不发生变化时，Argon2d的存储容量增加一倍，其计算量和存储器访问量也增加一倍，理论计算性能应该降低一半。存储器容量发生变化时，Argon2d在GPU上的性能如表5和图5b所示。在单个实例的存储器容量从128 KB增加到256 KB时，其性能下降为128 KB时性能的25.71%。可以看出，在GPU上执行这一类存储器难散列函数的最重要问题是显存容量有限，导致可以运行的线程数受限，从而降低了GPU利用计算过程隐藏存储器访问的能力，影响了系统的资源利用率和吞吐率。

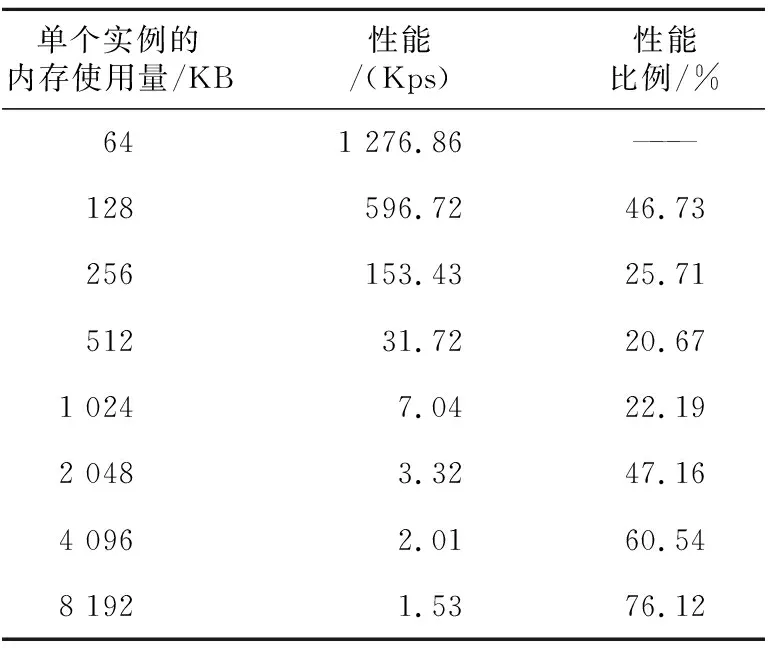
Table 5 Argon2d performance with different storage capacity (p=1, T=1)表5 Argon2d散列函数存储容量变化时的性能(p=1,T=1)

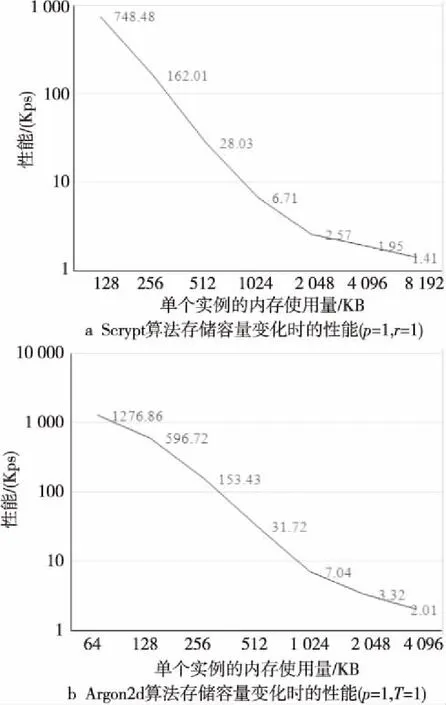
Figure 5 Performance vs storage capacity of Scrypt and Argon2d图5 存储容量变化时Scrypt和Argon2d的性能

在GPU上使用4线程协同计算和顺序存储方法计算存储器难散列函数，具有以下优点：(1)在相同的显存容量下，相对于1个线程计算1个实例，4个线程同时计算1个实例使得可以并发执行的线程数量增加4倍，增加了系统的并发能力。(2)在Salsa20/8的计算过程中，每个线程仅仅使用了4个32位字保存中间变量，寄存器使用量控制在32个字，提高了SM的使用率。(3)每个线程都使用16个字节的存储器访问而且采取了顺序存储方式，此时每个存储器请求包含了8个线程的存储器访问。由于使用了4个线程同时计算一个实例，存储器带宽利用率也从原有单线程模式的1/8提高到50%。

5 结束语

由于抗ASIC的特征，存储器难散列函数很有可能成为未来的口令散列函数。本文以典型的Scrypt和Argon2d为目标，研究了GPU上存储器难散列函数的性能优化方法，比较和分析了交织存储和顺序存储2种方法的存储器带宽利用率，指出使用16字节存储器访问和顺序存储方法可以更有效地利用GPU的存储器带宽。同时，本文提出了使用多个线程协作计算一个散列函数实例并使用warp间混洗函数交换数据的方法，有效减少了每个线程占用的资源，增加了可以并行运行的线程数量，更为有效地隐藏了存储器访存的延迟，并将存储器访问带宽的利用率提高到50%，较hashcat中的Scrypt实现，性能提升了2.03倍。

本文还使用4线程顺序存储方法实现了较为复杂的Argon2d散列函数，对于Argon2d依然具有较好的性能，说明了其对于不同存储器难散列函数的适应性。

本文比较了2种存储器难散列函数在不同存储器容量需求下性能的变化情况。实验表明，由于显存容量有限，可以并行执行的散列函数实例受到约束，减少了GPU上可以并发执行的线程数，使计算操作难以隐藏存储器访问延迟，从而降低了资源利用率，在GPU上执行散列函数的性能大幅度下降。

如何克服显存容量的瓶颈，保持可以并行工作的线程数量将是后续在GPU上优化实现存储器难散列函数的主要问题。