变形镜用高效率音圈驱动器的结构优化设计

曹 朔， 张志高， 赵子云， 顾 虎， 吴晶晶， 朱华新， 苏宙平， 张逸新， 胡立发*

(1. 江南大学 理学院，江苏 无锡 214122； 2. 江苏省轻工光电工程技术研究中心，江苏 无锡 214122)

1 引 言

1953年Babcock首次提出自适应光学的概念，即通过实时探测和校正光学系统的畸变，提高目标图像的分辨率[1]。1961年穆尔黑德提出了镀金属膜的聚酯薄膜变焦镜[2]。经过多年的研究开发，人们研制出了不同类型的变形镜：PZT变形镜[3]、电致伸缩变形镜[4]、薄膜变形镜[5]、MEMS变形镜[6]、音圈变形镜[7]等，并广泛应用于天文观测、显微成像、大功率激光、眼底成像等领域。其中，PZT变形镜是目前最广泛使用的变形镜。但因其磁滞特性、调制量相对低的缺点，限制了其在大口径望远镜次镜方面的应用。近年来，液晶以其优异的光电性能[8-10]，也用于波前校正器，是自适应光学系统的核心器件之一。相较于PZT变形镜，音圈变形镜的调制量大、无磁滞，同时还具有结构简单、体积小、噪声低、比推力高、响应速度快、精度高、维护方便、可靠性高等优点[11]。

1993年，意大利阿切特里天文台的Salinari提出了基于音圈驱动器的非接触变形镜[12]，并于1999年研制了30单元和36单元音圈变形镜，误差衰减可达100 Hz(0分贝衰减水平)[13]。2002年，MMT的336单元音圈变形镜研制成功，用作MMT望远镜的次镜，极大简化了自适应光学系统，提高了入射光的利用效率。其在H波段的斯特列尔比达到了0.2，在M波段的斯特列尔比达到了0.98[14-15]。2010年，有672个驱动器的音圈变形镜安装在LBT望远镜上，在H波段的斯特列尔比达到了0.8[16]。2012年正式运行的VLT巡天望远镜的变形次镜有1 170个音圈驱动器，所有模式的拟合误差RMS为62.5 nm[17]。E-ELT M4直径2.4 m，分为6个部分，由5 316个驱动器控制，最多可承受5%的驱动器故障，而不会破坏其性能[18]。Vecchio设计的永磁体径向磁化的音圈驱动器，功耗更低，结构更紧凑，但磁化过程复杂[19]。日本的Hashizume团队设计的音圈变形镜变形2.8 μm时，与理想抛物线的最大偏差小于30 nm[20]。国内多个研究组也开展了关于音圈变形镜的研究[21]。中科院光电技术研究所设计了动磁式音圈电机，输出力可达±0.5 N[22]，阶跃响应时间为50 ms，对离焦像差拟合PV值可达50 μm[23]。长春光机所通过音圈驱动器校正400 mm反射镜面形，经过校正后的RMS可达λ/40[24]。

音圈变形镜基本原理是音圈驱动器通过产生电磁力来驱动薄镜面变形，因此，在音圈变形镜的设计中，电机常数K是一个关键的参数，其定义为输出力与功耗的平方根的比值，是衡量电机电磁与热设计水平的标准，K值越大则驱动器效率越高[25]。在同样的形变量下，效率低的音圈驱动器会产生过多的热，热的积累导致温度升高，严重时导致薄镜面局部变形，最终会使变形镜的补偿精度和工作稳定性下降。最先应用于MMT望远镜的音圈驱动器的电机常数为0.6[26]，LBT望远镜的变形次镜单元中的音圈驱动器电机常数为0.74[27]，ELT望远镜中用于支撑镜面的音圈驱动器的电机常数达到1[28]。国内张玉方设计的用于薄镜面的动磁式音圈驱动器的电机常数为0.446[22]。赵静设计的采用Halbach阵列磁体的音圈电机的电机常数达到1.15，但是其径向排列的结构不适用于设计小口径的驱动器[25]。

目前研究较多的是动圈结构，固定的磁体可提供较强的磁场，但是运动的线圈散热差，对于需要快速响应的变形镜是个大的隐患。动磁式音圈电机由于尺寸限制无法提供较强的磁场，因此产生的电磁力较小。高效率的动磁式音圈电机的研究对于其应用尤为重要，本文针对该问题进行了研究，对音圈变形镜的结构设计进行了优化和仿真。

2 理 论

2.1 驱动器的基本结构

音圈驱动器常用的结构有两种：一种是动磁式，即磁体运动，线圈固定；另一种是动圈式，即磁体固定，线圈运动。基于动圈式的结构不利于工作过程中线圈的散热，因此，我们采用动磁式。基本结构如图1所示。

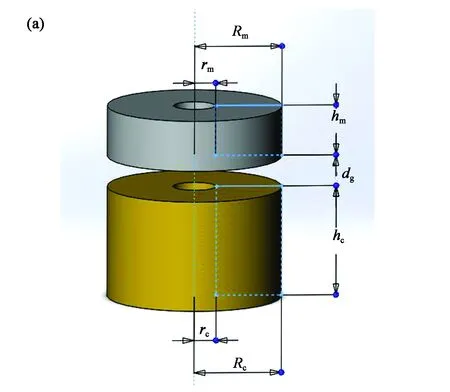
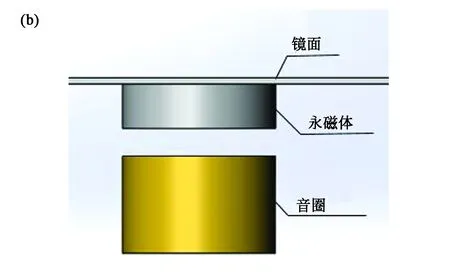
图1 (a)音圈驱动器结构图； (b)音圈驱动器与镜面的位置关系。Fig.1 (a)Structure diagram of voice coil actuator；(b) Position of voice coil actuator and mirror.

该音圈电机由上部粘在镜面背面的钕铁硼永磁体和下部铜线圈构成，主要参数如下：永磁体内外半径分别为Rm和rm，厚度为hm；线圈的内外半径分别为Rc和rc，厚度为hc；永磁体和线圈之间的气隙为dg。

2.2 电磁场分析

根据图1所示的基本结构，永磁体所产生的磁场是静磁场，其磁场分布可以按如下方法进行计算。首先，根据等效电流模型[29]，磁体内部存在的圆电流密度：

Jm=×M，

(1)

其中:M为磁化强度。在均匀磁化磁体内部圆电流抵消，而面电流密度为：

Jms=-en×M，

(2)

根据安培定律可求得磁体周围的磁感应强度：

(3)

其中:R是源点到场点的矢径，R是源点到场点的距离，V是永磁体体积，S是永磁体表面积。

通过虚位移法可以得到载流线圈在非均匀磁场中受到的合力为[30]：

Fi=IΦm，

(4)

其中Φm为线圈磁通量。设第i匝线圈半径为ri，距多层线圈上表面距离为di，其上任一点到磁体源点的距离：

(5)

该点处的磁感应强度：

(6)

其中：Ri为线圈上任一点到磁体源点的矢径。单匝圆线圈受到的安培力为：

(7)

其中：S是永磁体表面的面积矢量，方向为表面法线方向。多层线圈受到的合力为：

(8)

2.3 影响效率的因素

音圈驱动器的电机常数为：

(9)

其中:P是其功耗。

音圈驱动器的功耗为：

P=I2Rall，

(10)

其中:I为电流，Rall为线圈总电阻。将式(8)和(10)代入式(9)，可以得到评价驱动器效率的电机常数K公式如下：

(11)

由公式(11)可见，影响效率的主要因素包括磁感应强度、线圈尺寸和线圈电阻。

需要说明的是，上述公式在近似条件下，计算中心轴线等特殊位置处的磁场时可以得到近似准确的解，但实际情况下，磁体和线圈边缘的磁场分布复杂，我们需要借助有限元的方法进行求解。有限元分析已经广泛应用于各个领域，能够快速地求解电磁、热、流体、结构等问题，节约研发成本，减少研发时间。有限元法是将待求解的整体分割成许多足够小的子区域，即“有限元”，然后根据求解边界问题的原理求解这些有限元，求得的所有结果合起来就是整体的解。Ansoft Maxwell进行三维网格剖分时将求解区域剖分为许多四面体单元，如图2所示。

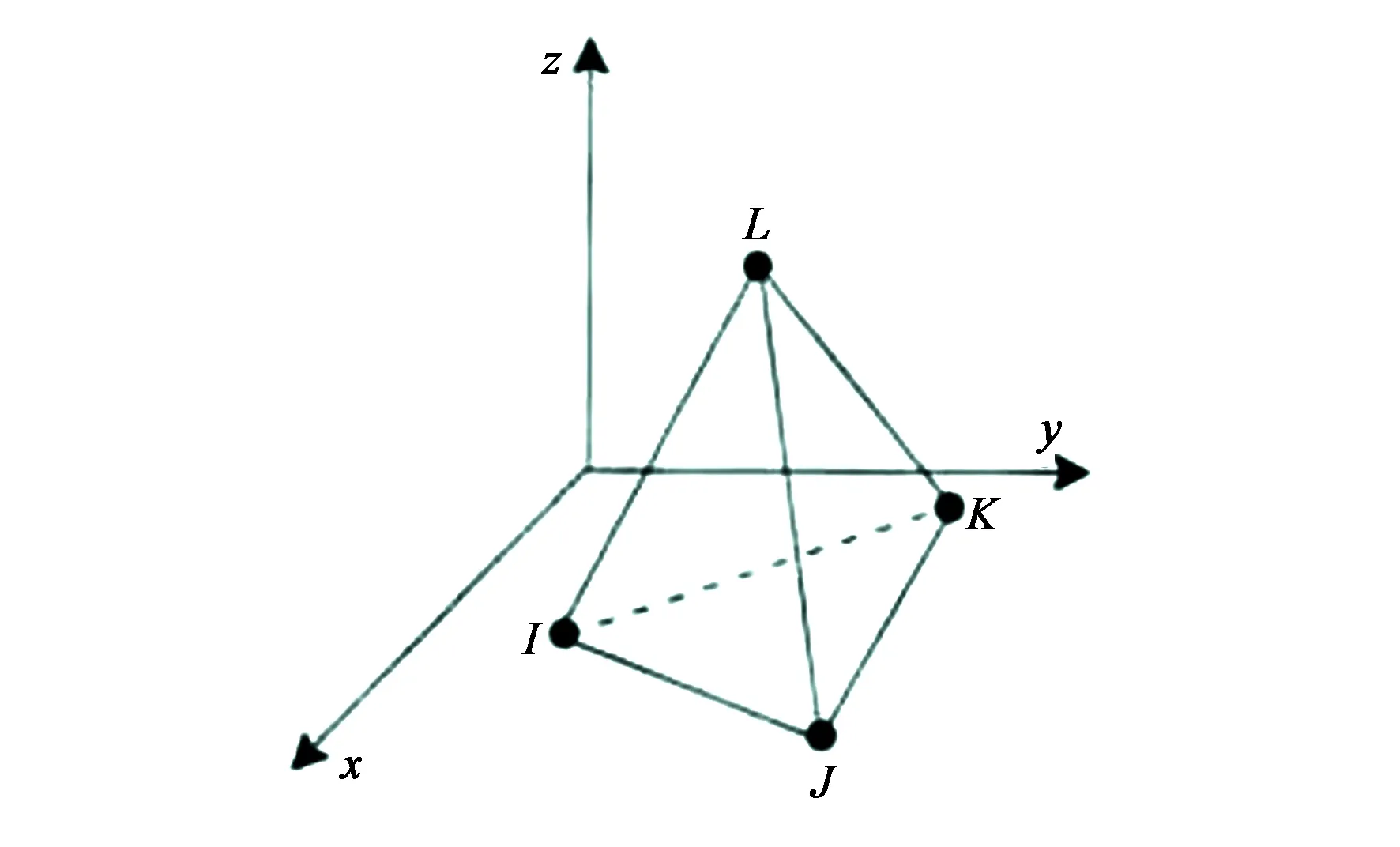
图2 有限元计算基本单元Fig.2 Basic element of finite element calculation

4个顶点上的场量为：

(12)

求解该方程组需要4个顶点的坐标和定点上的场量。

三维静磁场采用棱边法计算，以单元边上的待求场量为自由度。磁场强度H为

H=HP+φ+HC，

(13)

其中：φ为标量磁位，Hp为四面体单元6条棱边上待求的磁场强度。四面体4个顶点上的标量磁位和6条边上的磁感应强度组成了待求解的10个自由度，最后采用二次插值逼近每个单元内的场量[31]。Maxwell软件进行有限元仿真的步骤为：建模，添加材料，添加边界条件和激励，划分网格，后处理。为了得到高精度的结果，要特别注意网格的质量以及边界条件和激励的合理性。

3 仿真结果与分析

由前述的解析公式可以看出，驱动器的输出力跟以下因素有关：永磁体的充磁方向和磁体线圈间的气隙厚度、磁体和线圈的几何尺寸等关键参数。但上述解析公式只针对特殊位置有精确的解，为了进一步研究驱动器参数对音圈变形镜性能的影响，我们利用有限元算法进行了精确的模拟。本节分别对这些参数的影响进行了仿真模拟与讨论。

3.1 磁场方向的优化对比

设置线圈外径为10 mm，内径为1 mm，高度为6 mm，导线直径为0.33 mm；永磁体外径为10 mm，内径1为mm，高度为3 mm，分别设置磁体的充磁方向为径向充磁和轴向充磁，永磁体轴向受力和电流关系如图3所示。图中横轴为输入电流i，纵轴为永磁体在轴向所受的电磁力，结果显示永磁体受力Fz与输入电流成正比，可用式(14)表示：

Fz=k·i，

(14)

其中：k是比例系数，对于径向充磁和轴向充磁的磁体k分别是0.45和0.34。可见，径向充磁的永磁体所受电磁力更大。因此，接下来的实验中都选用径向充磁的永磁体。

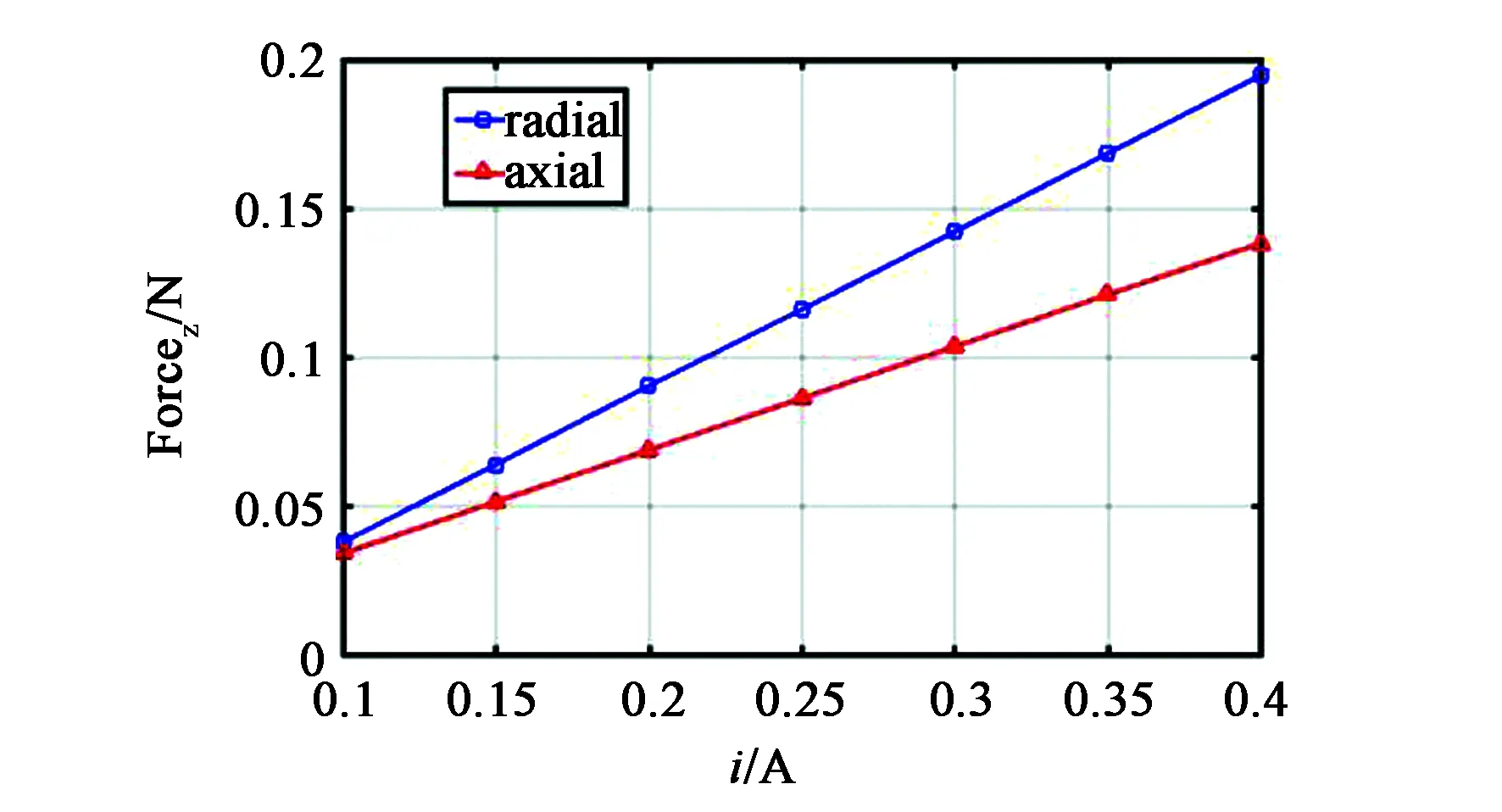
图3 电磁力与磁体不同充磁方向的关系Fig.3 Relationship between electromagnetic force and different magnetization directions of magnet

3.2 气隙厚度

磁体和线圈之间的气隙为变形镜的镜面局部形变提供空间，当间隙较大时，镜面相同的形变量需要更大的驱动力，而这需要更大的输入电流，增加了功耗和热；而当间隙较小时，这会限制镜面的局部形变，减少它的调制量。因此，需要对驱动器的形变进行优化设计。线圈尺寸为：外径10 mm，内径1 mm，高度6 mm；导线直径0.33 mm，通入电流0.2～0.5 A，步长0.1 A；磁体外径10 mm，内径1 mm，高度3 mm，设置磁体与铜线圈之间的气隙厚度dg为0.1～1 mm，步长0.1 mm，仿真结果如图4所示。图4中横轴为永磁体与铜线圈之间的气隙厚度dg，左纵轴为永磁体的轴向受力，右纵轴为电机常数K，结果表明气隙的增大会导致电磁力和电机常数减小，所以气隙应在满足驱动器最大行程条件下取最小值。MMT望远镜的音圈驱动器的气隙为0.1 mm，满足运行时所需的行程空间[13]，因此本文选择气隙厚度为0.1 mm。

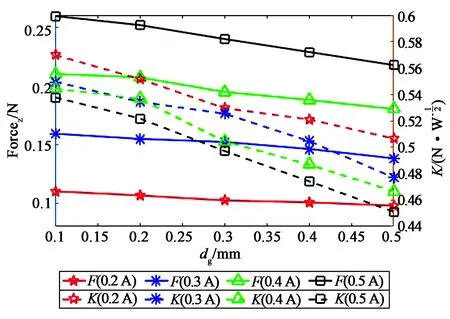
图4 电磁力随气隙厚度的变化关系Fig.4 Relationship between electromagnetic force and air gap thickness

3.3 磁体结构优化

3.3.1 磁体厚度的优化

图5 电磁力和电机常数随磁体高度变化的关系Fig.5 Relationship between electromagnetic force,actuator constant and the height of magnet.

驱动器的基本结构如图1所示，为了优化线圈的尺寸，线圈的外径增加时，会影响其空间密度，而外径太小时，输出的电磁力较弱，会导致调制量降低，因此，线圈外径采用10 mm，通过优化磁体高度，来优化其性能。首先，我们固定线圈外径10 mm，内径1 mm，高度6 mm；导线直径0.33 mm，通入电流0.2～0.5 A，步长0.1 A；磁体外径10 mm，内径1 mm，设置高度hm取值1 ～10 mm，步长1 mm，仿真得到磁体高度与电磁力的关系如图5所示。图中横轴为永磁体的高度hm，左侧纵轴为永磁体的轴向受力，右侧纵轴为电机常数，结果显示随着磁体高度的增加电磁力也变大，但是电磁力与电机常数的增长幅度变小。考虑到磁体的成本，选择磁体高度为3 mm。

3.3.2 磁体外半径优化

固定线圈外径10 mm，内径1 mm，高度6 mm；导线直径0.33 mm，通入电流0.2～0.5 A，步长0.1 A；磁体内径1 mm，高度3 mm，设置磁体外半径Rm取值3～7 mm，步长0.5 mm，仿真结果如图6所示。图中横轴为永磁体外半径Rm，左纵轴为永磁体轴向受力，右纵轴为电机常数。结果显示随着永磁体外半径变大电磁力和电机常数也变大，但外径大于5 mm时电磁力和电机常数的增长幅度开始减小，因此选择永磁体外径为5 mm。

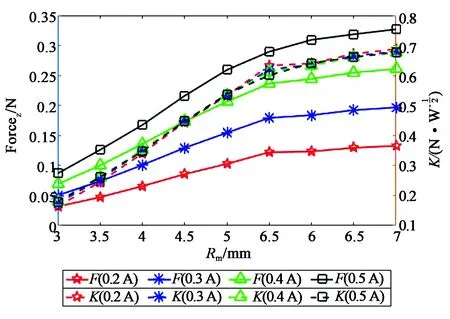
图6 电磁力和电机常数随磁体外径变化的关系Fig.6 Relationship between electromagnetic force,actuator constant and the outer diameter of magnet.

3.3.3 磁体内半径优化

固定线圈外径10 mm，内径1 mm，高度6 mm；导线直径0.33 mm，通入电流0.2～0.5 A，步长0.1 A；磁体外径10 mm，高度3 mm，设置磁体内半径rm取值0.3～0. 7 mm，步长0.1 mm，仿真结果如图7所示。 图中横轴为永磁体内半径rm，左纵轴为永磁体轴向受力，右纵轴为电机常数，结果显示磁体内径变化时电磁力没有明显变化，但当磁体内半径从0.1 mm增至0.5 mm时，电机常数变大并达到极值，然后随着磁体内径的增大而减小，因此选择磁体内半径为0.5 mm。

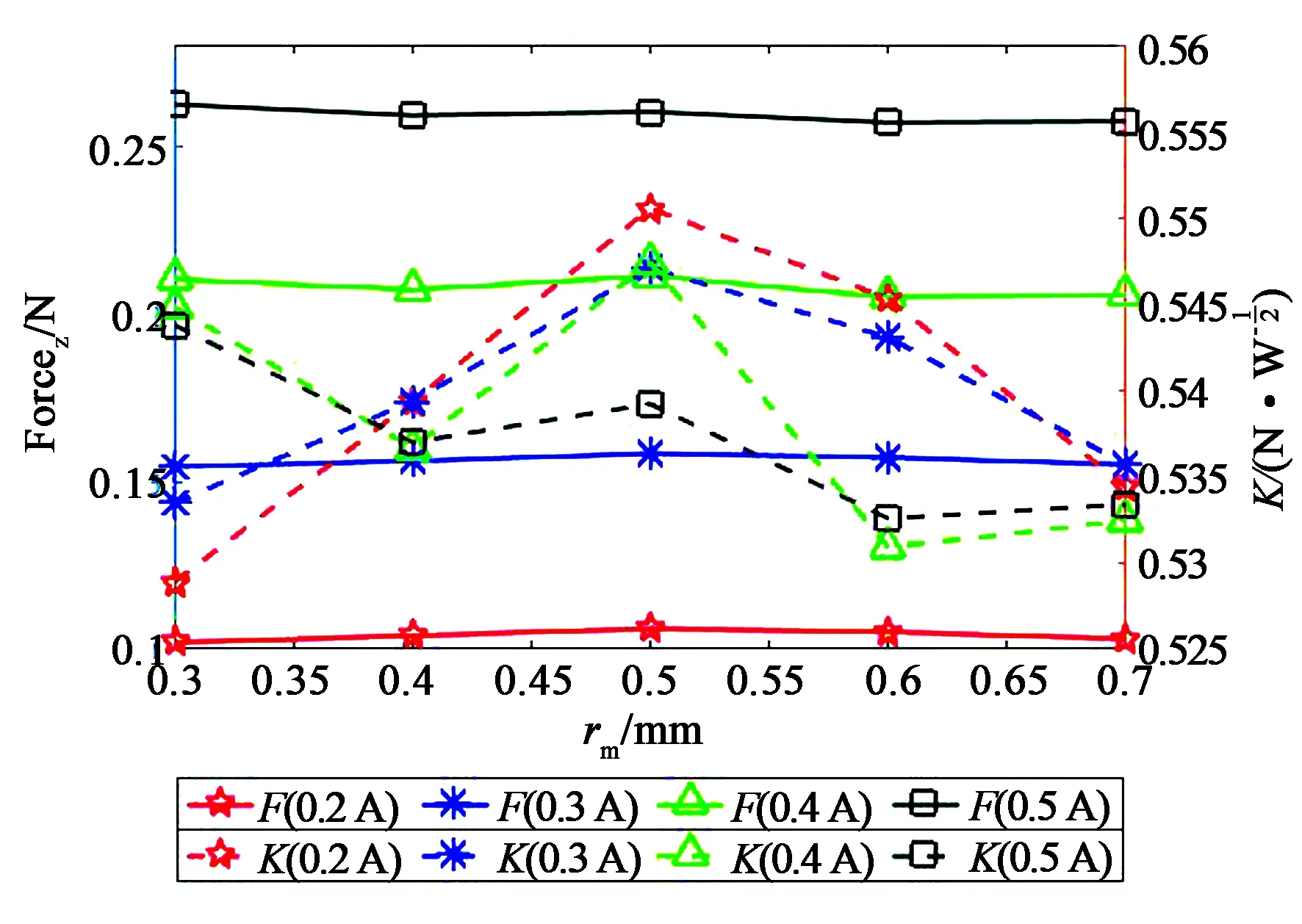
图7 电磁力和电机常数随磁体内径变化的关系Fig.7 Relationship between electromagnetic force,actuator constant and the inner diameter of magnet.

3.4 线圈结构优化

3.4.1 线圈高度

图8 电磁力和电机常数随线圈高度变化的关系Fig.8 Relationship between electromagnetic force,actuator constant and the height of coil.

固定磁体外径10 mm，内径1 mm，高度3 mm；导线直径0.33 mm，通入电流0.2～0.5 A，步长0.1 A；线圈外径10 mm，内径1 mm，高度hc为4～8 mm，步长1 mm，仿真结果如图8所示。图中横轴为线圈高度h，左侧纵轴为永磁体轴向受力，右侧纵轴为电机常数。随着线圈高度的增长磁体受力增长而电机常数减小，综合考虑电磁力和电机常数，选择线圈高度为6 mm。

3.4.2 线圈外径

固定磁体外径10 mm，内径1 mm，高度3 mm；导线直径0.33 mm，通入电流0.2～0.5 A，步长0.1 A；线圈内径1 mm，高度6 mm，外半径为4～6 mm，步长0.5 mm，仿真结果如图9所示。图中横轴为铜线圈外半径Rc，左纵轴为永磁体轴向受力，右纵轴为电机常数。结果显示随着线圈外径的增大，电磁力逐渐增大，而电机常数在Rc=5 mm处达到极大值，因此选择线圈外半径为5 mm。

图9 电磁力和电机常数随线圈外径变化的关系Fig.9 Relationship between electromagnetic force,actuator constant and the outer diameter of coil.

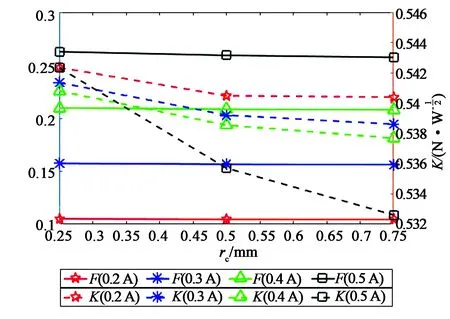
图10 电磁力和电机常数随线圈内径变化的关系Fig.10 Relationship between electromagnetic force,actuator constant and the inner diameter of coil.

3.4.3 线圈内径

固定磁体外径10 mm，内径1 mm，高度3 mm；导线直径0.33 mm，通入电流0.2～0.5 A，步长0.1 A；线圈外半径5 mm，高度6 mm，内半径为0.25 mm，0.5 mm，0.75 mm，仿真结果如图10所示。图中横轴为线圈内半径rc，左侧纵轴为永磁体轴向受力，右侧纵轴为电机常数。结果显示随着线圈内径的变大，电磁力没有明显变化，而电机常数虽然减小但数值变化不大，考虑到电机的结构，因此选择线圈内半径为0.5 mm。

3.5 输出力的线性

经过Maxwell的仿真优化，该音圈电机结构参数如下：永磁体外半径5 mm，内半径0.5 mm，高度3 mm，磁体径向充磁；线圈外半径5 mm，内半径0.5 mm，高度6 mm；通过仿真表明输入电流和电磁力有良好的线性关系，如图11所示。

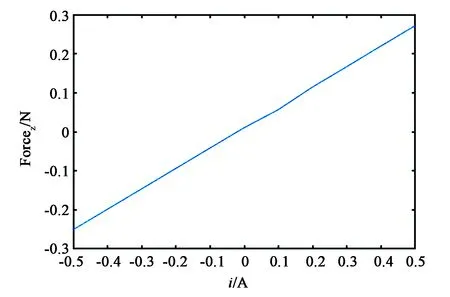
图11 电磁力和电流的关系Fig.11 Relationship between electromagnetic force and current

4 双线圈结构音圈电机

(a)双线圈音圈电机结构图(a)Structure of voice coil actuator with double coils

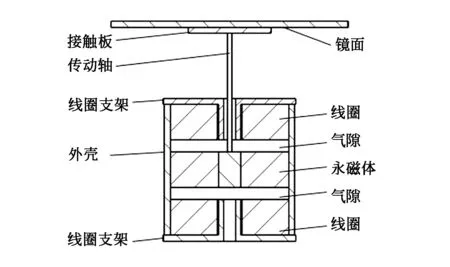
(b)双线圈音圈电机剖面图(b)Section of voice coil actuator with double coils图12 双线圈音圈电机结构图Fig.12 Structure diagram of voice coil actuator with double coils

经过优化的音圈电机的电机常数约为0.6，与MMT望远镜的音圈电机的效率相当。为了进一步提高效率，在此基础上设计了一种新的结构，如图12。将6 mm厚的铜线圈分为两个厚度为3 mm的铜线圈，分布于磁体两侧，气隙厚度0.1 mm，其余尺寸均与第三节相同。两个线圈分别位于永磁体两侧，提高了磁场的利用率，而且通过传动轴对镜面进行推拉减小了驱动器热量对镜面的影响。

4.1 磁场强度的仿真与对比

通电线圈激发的磁场越大永磁体受力越大，以两种结构的线圈在永磁体半高处产生的磁场强度为例，仿真结果如图13所示。横轴为直径上的点，纵轴为该点处的磁场强度，双线圈结构产生的磁场强度为H1,单线圈产生的磁场强度为H2。结果表明双线圈结构可以在永磁体处产生更大的磁场强度。

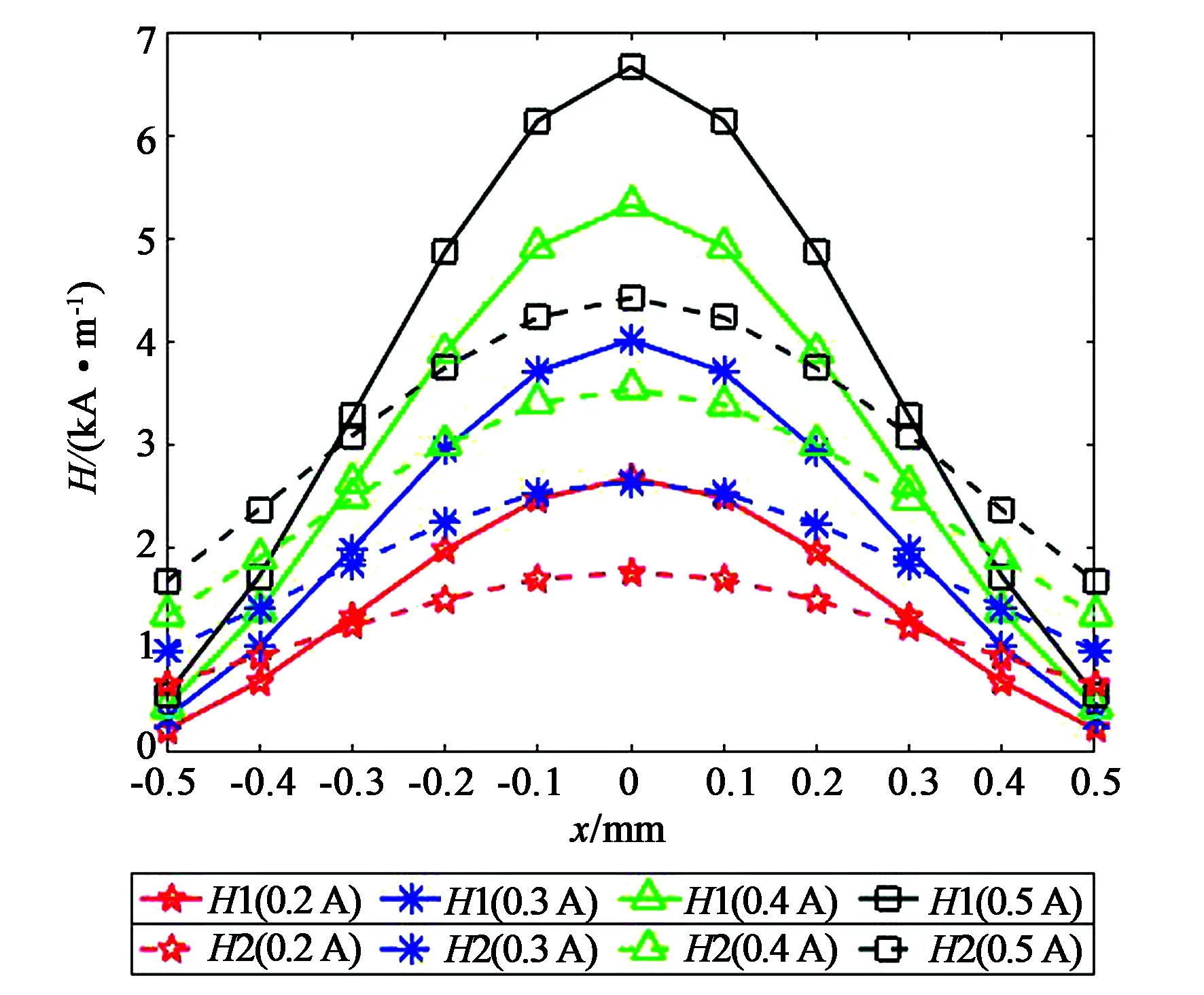
图13 双线圈和单线圈产生的磁场强度对比Fig.13 Comparison of magnetic field strength generated by double coils and single coil

4.2 电磁力的仿真与对比

图14展示了双线圈电机(CMC)和单线圈电机(MC)通入不同电流得到的电磁力和电机常数，图中横坐标为通入的电流i，左纵轴为永磁体轴向受力，右纵轴为电机常数，结果显示双线圈电机可以产生更大的推力和电机常数。

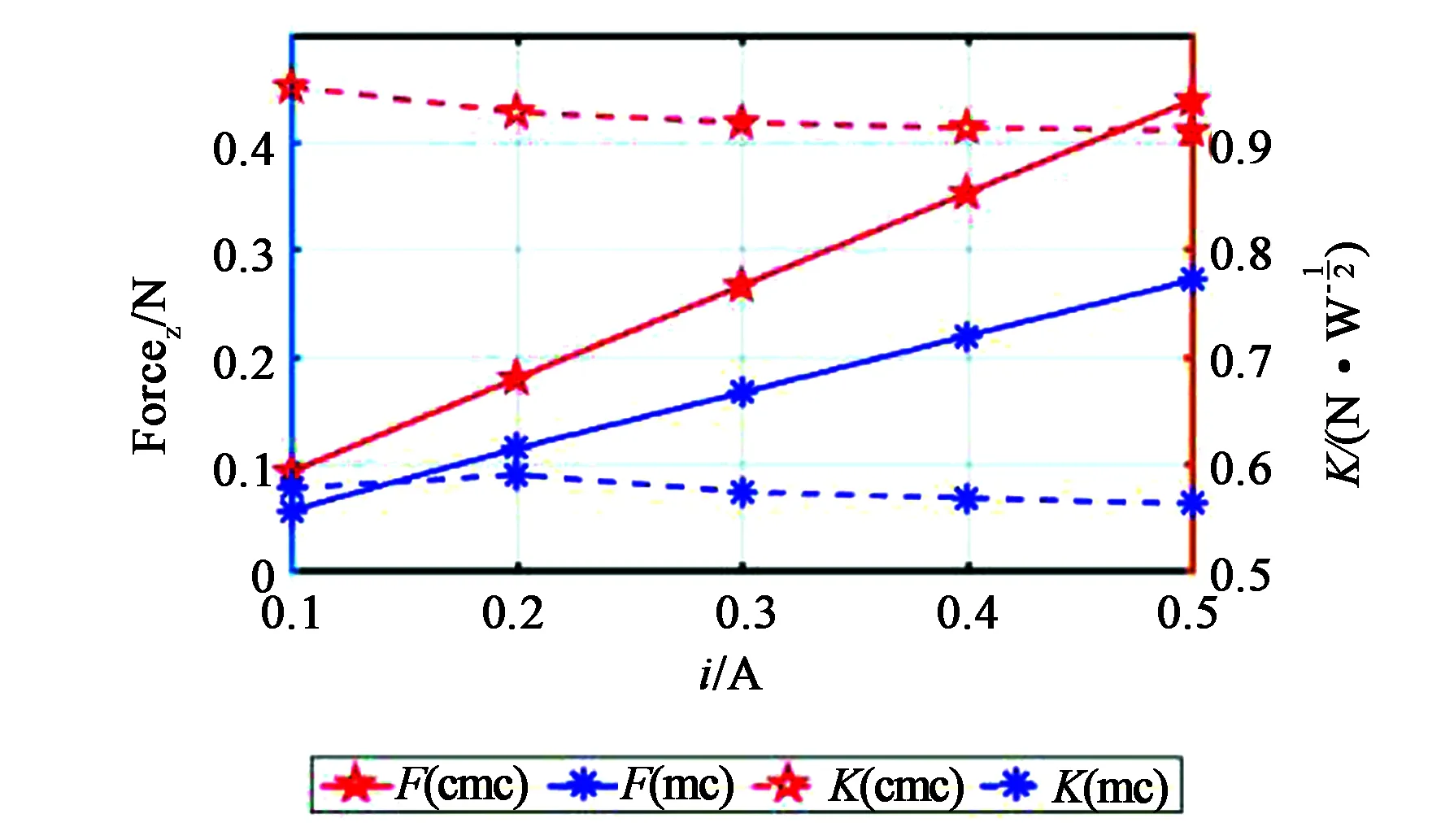
图14 两种电机的电磁力和电机常数Fig.14 Electromagnetic force and actuator constant of two actuators

5 结 论

本文设计了用于变形镜的动磁式高效率音圈驱动器。介绍了音圈驱动器的基本原理并且推导了计算音圈驱动器电磁力的公式。基于有限元的方法利用Maxwell软件对动磁式音圈电机进行了模拟仿真，结果表明采用径向充磁的永磁体提高了电机的效率，降低了发热。通过对磁体和线圈的尺寸进行优化将电机常数提高至0.9，输出力达到0.43 N。结果符合电机设计的基本要求，为音圈驱动器的研制提供了理论基础。