灰色统计模型在辽河平原灌区地下水埋深预测的的适用性分析

孟庆玉

(朝阳市喀左县水利局，辽宁 喀左 122300)

1 概 况

辽河平原位于辽宁的中部，处于辽东和辽西山丘之间，从铁岭到阜新彰武的南端，一直到辽东湾入海，为辽宁省沉降一级区，辽河平原地下水资源较为丰富，主要地形堆积为冲击平原，且在辽河干流发育冲击洪谷，下辽河地形从南向北逐步发生倾斜[1-2]。辽河平原区的地下水主要富集在第三系碎屑岩孔隙和裂隙中[3]。地下水分布可划分两个分区带，第一个分区带主要分布在石佛寺及辽滨的东部，这一分区地下水资源量较为丰沛，单井水量可保持在3000-5000m3/d之间，第二个分区主要分布在营口以西的地区，这一区域水量主要为地下径流的补给，两个分区地下水排泄方式均为人工开采。彭博的研究表明辽河平平原由于地下水开采布局的原因使得区域地下水位下降较为明显。辽河平原部分地下水开采井较为密集的区域出现面积较大的漏斗，漏斗中心的水位可达到46m，主要分布在新兴以及兴隆台区域[4-5]。辽河平原灌区覆盖面积较大，主要的农作物为水稻和玉米，其中水稻需水量较大，而由于区域地处大陆季风性气候，年降水量在600-800mm左右，夏季易出现旱情，影响农作物的正常生产[6]。近些年来，为保障区域农业供水量，除水利工程供水措施外，辽河平原也通过增加地下水开采井来进行水量的供给，使得区域地下水资源量呈现逐年递减变化[7]。从2013年开始，辽河平原灌区加大了对地下水资源的有效配置措施，合理规划各开采井的压采量，使得辽河平原灌区地下水资源量有所回升[8]。为加大对辽河灌区地下水资源的保护，需对区域地下水变化趋势进行预测，从而进一步调整各地下水开采井的压采量，为此文章结合在国内地下水预测效果较好的灰色统计模型，对辽河平原灌区的地下水进行预测，从而为区域地下水优化配置提供重要的支撑依据[9-11]。

2 灰色统计模型原理

灰色统计模型主要结合二次回归方程的原理，通过实测数据作为回归样本，建立模型，对模型变量进行预测，回归方程为：

(1)

其中记系数向量

(2)

灰色统计模型结合最小二乘法对模型进行优化求解：

(3)

式中：X为实测数据的样本系列；a为模型回归方程系数；u为回归变量系数；变量B和YN分别为模型的求解变量，求解方程为：

YN=[X(0)(2),X(0)(3),…X(0)(N)]T

(4)

灰色统计模型不同时段下的求解方程为：

(5)

灰色统计结合变量的不同权重值对地下水位变量进行预测：

(6)

在方程中T和B分别表示灰色统计模型的上限和下限条件。

3 模型应用及结果分析

3.1 站点概况

结合辽河平原灌区地下水资源的分布特点，选取两个地下水监测井进行模型的检验，第一个地下水观测井分布在石佛寺及辽滨的东部，第二个地下水观测井分布在营口以西的地区。第一个观测井的单井出水量在1000-30000m3/d之间，地下水埋深观测数据的系列长度为59a，第二个观测井的单井出水量在2000-4000m3/d之间，地下水埋深的观测数据系列长度也为59a。两个地下水观测井主要为辽河平原灌区灌溉用水服务，并重点对区域的地下水埋深进行有效监测，文章以这两个典型地下水观测井作为分析井点，分析灰色统计模型在区域地下水预测的适用性。

3.2 回归方程的检验

基于各观测井年尺度、季节尺度、月尺度地下水埋深数据，建立多元回归方程，并分别采用F检验和T检验对各时间尺度的回归方程进行检验，检验结果见表1、表2及表3。

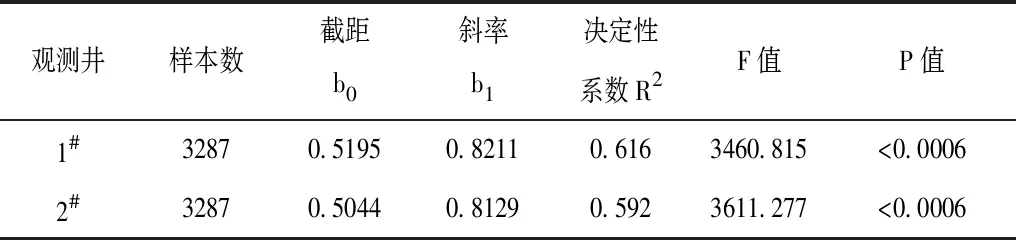
表1 辽河平原灌区地下水观测井年尺度回归方程检验结果

表2 辽河平原灌区地下水观测井月尺度回归方程检验结果

表3 辽河平原灌区地下水观测井季节尺度回归方程检验结果

从年尺度回归方程分析结果可看出，地下水井日地下水埋深变幅总体较小，因此采用线性回归构建辽河平原灌区地下水埋深的回归方程，从年地下水埋深的决定性系数可看出，决定系数分别为0.616和0.592，低于0.7，这主要是因为辽河平原灌区各地下水观测井地下水埋深年尺度变幅影响较大，因此线性回归方程的决定系数不高，但从F检验结果可看出，其可通过F检验，达到95%的置信水平，满足模型地下水日埋深的预测要求[12-14]。表2为辽河平原典型灌区月尺度回归检验结果，从回归方程的检验结果可看出，其相关系数均高于0.9，这表明月尺度的建立的回归方程的相关度较好，从其T检验值也可看出，均可通过95%的T检验水平。由于不同季节辽河平原灌区地下水埋深变化差异较为明显，为此在日尺度和月尺度回归方程检验的基础上，对不同季节辽河平原灌区两个地下水观测井回归方程检验结果可看出，春季和秋季各观测井地下水埋深建立的回归方程的决定系数要高于夏季和冬季地下水埋深回归方程的决定系数，这主要是因为春季和秋季地下水埋深受人工压采影响较小，而夏季辽河平原灌区由于地下水开采量增加，使得地下水埋深受到人工压采量的增加影响较为明显，其决定系数降低。而冬季由于地下水补给量减少，使得其地下水埋深较低，影响其回归方程的决定系数，冬季建立的观测井回归系数低于其他季节，但从不同季节的F值检验结果可看出，均可通过95%的F检验。

3.3 预测精度分析

在灰色统计模型回归方程检验基础上，基于构建的年地下水埋深回归模型对两个地下水观测井年尺度地下水埋深进行预测，并和BP神经网络模型进行精度对比，对比结果分别见表4和表5。

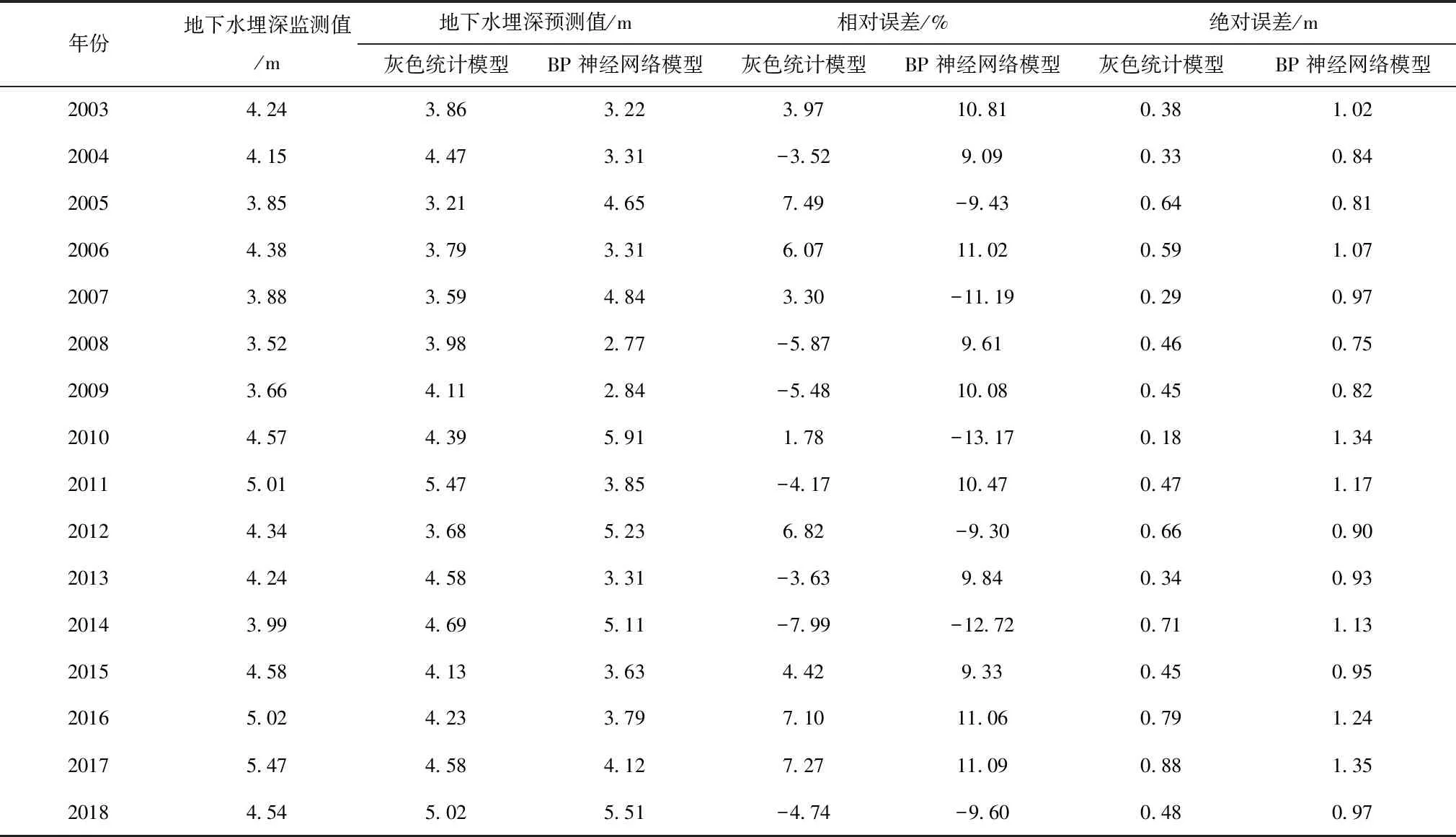
表4 1#观测井地下水埋深预测的精度分析结果

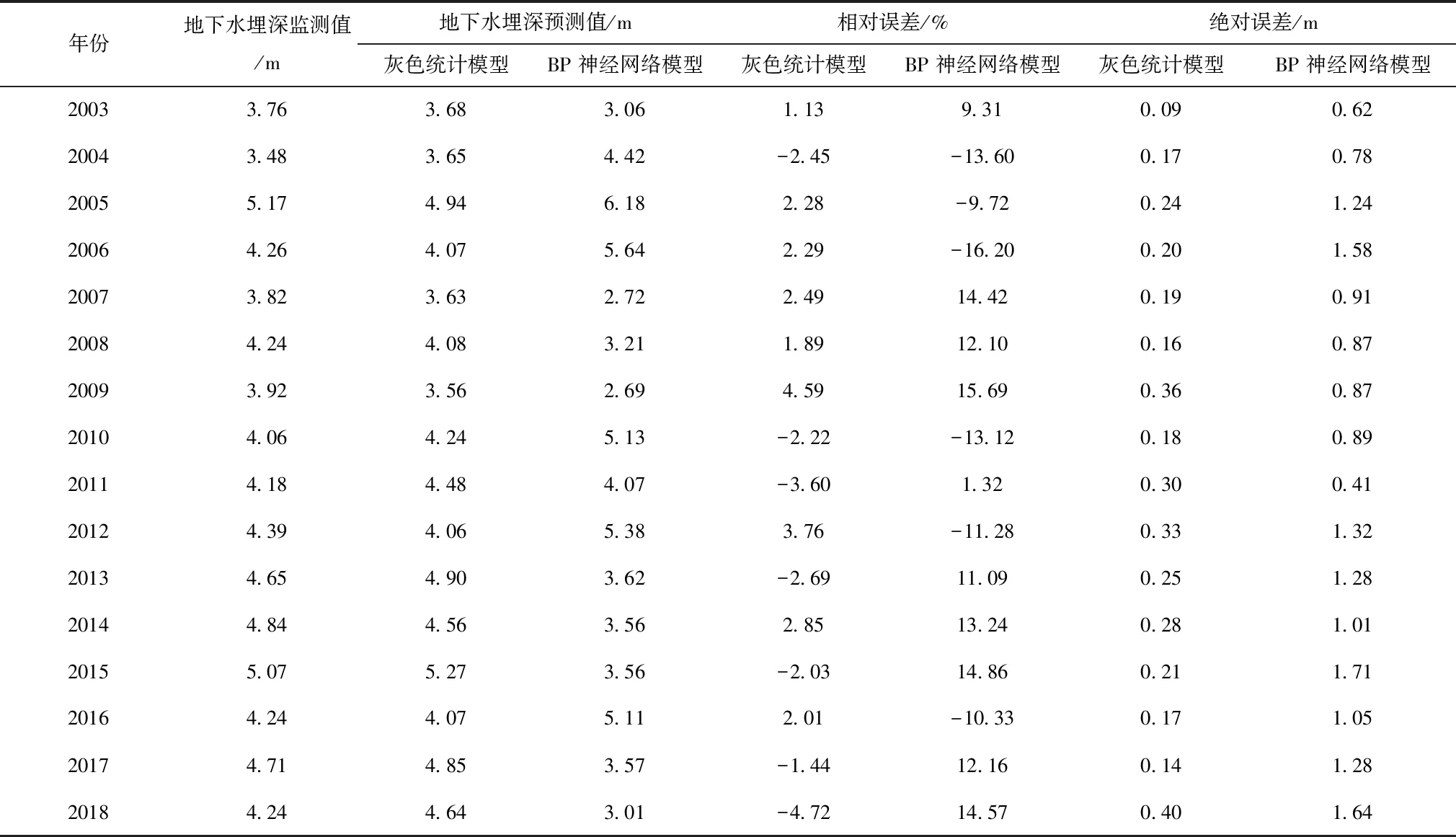
表5 2#观测井地下水埋深预测的精度分析结果

从第一个地下水观测井的对比结果可看出，灰色统计模型预测的各年份地下水埋深的相对误差均低于10%，相比于BP神经网络模型，相对误差的平均值减少5.26%，灰色统计模型预测的第一个观测井地下水埋深相对误差在0.18-0.88m之间，而BP神经网络模型下预测的地下水埋深绝对误差均高于同年份灰色统计模型下的绝对误差值，相比于BP神经网络模型，灰色统计模型在绝对误差上，平均降低0.51m，可见在辽河平原灌区选取的第一个地下水观测井，灰色统计模型具有较好的适用性。从表2中可看出，和第一个观测井地下水埋深预测误差较为相似，第二个观测井下灰色统计模型预测精度也好于BP神经网络模型，相对误差和绝对误差都较BP神经网络模型有明显改善。这主要是因为灰色统计模型对回归方程变量进行权重分析，通过合理设置不同变量的影响权重，来提高回归方程的精度，尤其是对于地下水埋深预测而言，由于地下水埋深受人工开采影响程度较高，因此各变量影响因素较多，BP神经网络模型变量预测大都基于天然条件下，对于人为影响因素难以考虑，因此对于区域地下水，尤其是地下水开采量较大的区域，其预测精度较低。

4 结 论

1)灰色统计模型由于可设置变量权重，来优化模型精度，尤其是可考虑人为影响较大变量预测，适合于地下水埋深的预测，在辽河平原灌区地下水埋深预测精度要好于传统回归模型的精度。

2)在构建灰色统计模型回归方程后，需要结合T检验和F检验对回归方程进行误差检验，而不能单纯考虑相关系数确定回归方程的合理性。