软土盾构近距离下穿地铁双圆隧道变形实测分析

刘颖彬，廖少明，*，陈立生，柳毅强，顾颖成

(1.同济大学地下建筑与工程系，上海 200092；2.上海城建市政工程(集团)有限公司，上海 200065)

0 引言

盾构下穿既有建(构)筑物是城市基础设施建设中常见的工程问题。随着相关施工技术、理论研究的不断进步以及施工经验的不断积累，盾构下穿常规既有建(构)筑物的技术体系已经相对成熟和完善，穿越效果也越来越接近于"零沉降"。但是，对于盾构穿越双圆隧道等异形结构形式或特殊功能的建(构)筑物，仍存在诸多问题与挑战。

目前，众多学者针对盾构穿越运营地铁单圆隧道开展了一系列研究，其中包括盾构上穿运营隧道[1]、下穿运营隧道[2]、上下夹穿运营隧道[3]以及盾构隧道群下穿运营隧道[4]等工程的实测分析以及不同工程的相应施工控制措施[3-7]等。在双圆隧道方面，周文波等[8]对双圆盾构施工主要技术难点进行了剖析，初步摸索出一整套适用于双圆盾构的施工工艺；袁金荣等[9]总结出几种计算模型对双圆盾构隧道结构计算的适应性，发现双圆隧道结构对计算参数具有显著的敏感性；周文波等[10]通过原位测试方法对盾构隧道管片在不同施工阶段的受力进行分析，指出管片在不同施工阶段的结构内力变化特点；翁承显等[11]根据实测数据统计分析总结出双圆隧道引起地表沉降槽的形态特征，并提出了沉降槽宽度范围的估算公式；张兆逵等[12]结合具体工程阐述了双圆盾构施工引起的地面沉降与各项影响因素的关系；魏纲等[13]采用三维MIDAS/GTS软件，考虑到建筑物-土体-隧道共同作用，对双圆盾构隧道施工引起的建筑物附加沉降及荷载进行了研究；魏纲等[14]采用椭圆形非等量径向位移模式的土体变形方法，推导出双圆盾构隧道施工对平行既有隧道的附加荷载影响与2条隧道相对位置密切相关；曾彬等[15]通过实例计算得出了双圆盾构隧道施工偏转角将导致地表附加变形的结论；郭璇等[16]通过系列正交试验考察软土层与双圆盾构衬砌相互作用的参数效应，得到软土层作用下双圆盾构衬砌的结构内力响应和各地层沉降曲线的影响规律；李筱旻[17]通过实测和数值分析的方法得到，在道路施工中，采用EPS换填技术可以减小道路填方施工对下卧双圆隧道的不利影响；陈小亮等[18]构建三维弹塑性有限差分模型，计算分析双圆盾构掘进引起的地表位移场以及土体应力场分布，并将数值模型计算结果和现场监测数据进行对比验证；丁智等[19]基于2.5维有限元法首次建立双圆地铁列车-轨道-地基土分析模型，分析双圆地铁运行荷载下隧道埋设深度、列车行车速度等重要因素对地基及轨道振动的影响。综上可知，双圆隧道现有研究成果多集中于双圆盾构隧道本体结构、双圆盾构施工控制和环境影响方面，在盾构下穿双圆隧道方面研究较少。双圆隧道的异形断面使得其纵横向不均匀变形变得极为敏感，本文以上海地铁14号线盾构下穿地铁6号线双圆隧道工程为背景，通过现场实测分析盾构下穿双圆隧道过程中隧道的变形特征与变化规律，以期探明盾构穿越过程中双圆隧道结构的纵横向受力变形的特点。

1 工程概况

上海地铁14号线云山路站-蓝天路站区间为盾构法圆形隧道区间，区间覆土厚度为9.6～17.2 m，2条线最小线间距为16.14 m，线路长度约为1 067.08 m，采用直径为6 760 mm土压平衡盾构施工，盾构长度为9.55 m，隧道内径为5.9 m，外径为6.6 m，环宽为1.2 m，环厚为0.35 m。盾构在云山路与张杨交叉口下穿运营地铁6号线双圆隧道区间，6号线隧道外径为6.3 m，宽度为10.3 m，环度为1.2 m，环厚为0.3 m。2条相交隧道角度接近90°，2条隧道交叉区域宽度约10 m。地铁6号线双圆隧道与本工程上行线交叉环号为849-859，与下行线交叉环号为850-860。双圆隧道底部与盾构隧道最小竖向距离为5.05 m。14号线盾构主要穿越上海典型高灵敏度饱和软黏土地层，即④层灰色淤泥质黏土、⑤1-1灰色黏土层以及第⑤1-2层灰色粉质黏土层。地层主要力学参数如表1所示。盾构穿越双圆隧道平面如图1所示。盾构穿越双圆隧道剖面如图2所示。

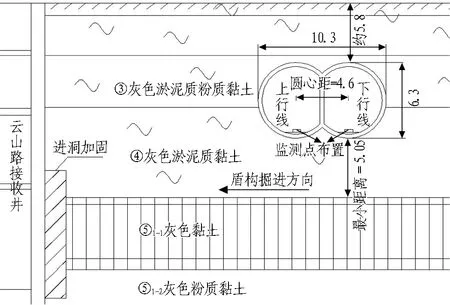
图2 盾构穿越双圆隧道剖面图(单位：m)Fig.2 Profile of shield crossing DOT tunnel (unit:m)

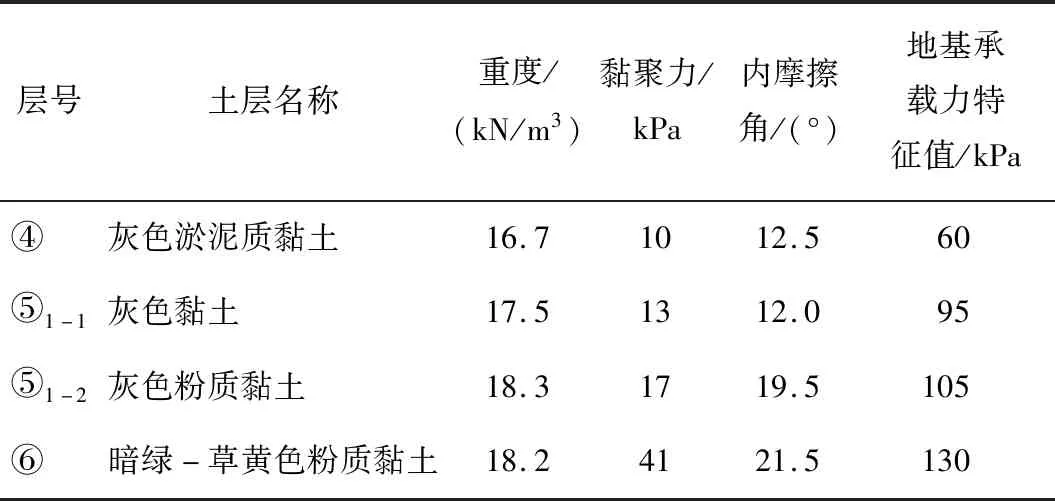
表1 地层主要力学参数Table 1 Mechanical parameters of soils

穿越区域划分为3个区域，如图1和表2所示。

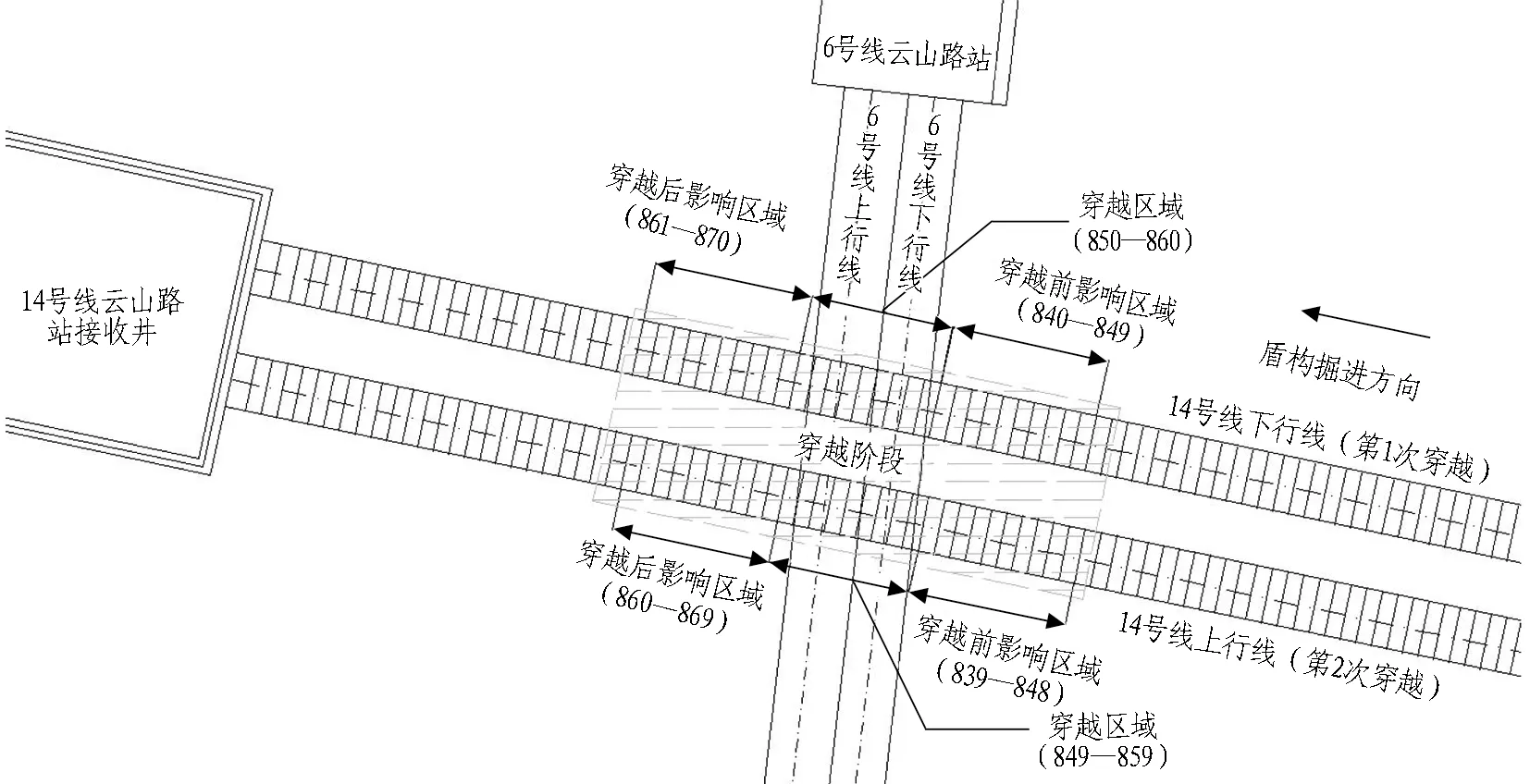
图1 盾构穿越双圆隧道平面图Fig.1 Plane of shield crossing DOT tunnel

表2 穿越区域划分Table 2 Partition of undercrossing area

为了减少2次穿越之间的相互影响，2次穿越在时间上设置了间隔。14号线下行线盾构于2019年9月17日推进至839环，进入穿越前影响区域，9月21日盾尾离开859环，第1次穿越结束；2019年10月9日14号线上行线盾构推进至840环，盾构切口进入穿越前影响区域，10月12日盾尾离开860环，穿越施工结束。

2 监测方案

在盾构穿越前，沿着双圆隧道上、下行线轴线分别布置了电子水平尺测点，共布置98个测点(6号线上行线SU08-SU56，6号线下行线XU08-XU56)，对双圆隧道竖向位移进行测量。其中测点28是双圆隧道与盾构下行线掘进轴线的交叉点，测点36是双圆隧道与盾构上行线的掘进轴线交叉点，上、下行线测点之间的距离为4.6 m，轴线上各测点的间距是2 m。测点布置如图3所示。本文选取盾构掘进过程中关键施工参数的每环平均值作为依据，分析各阶段施工参数对隧道变形的影响。

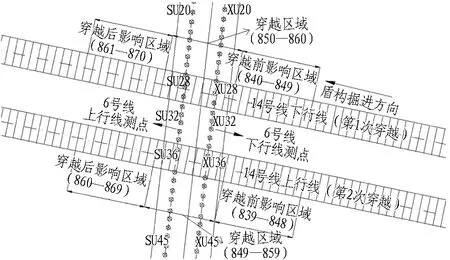
图3 地铁双圆隧道测点布置图Fig.3 Layout of field measurement for DOT metro tunnel

3 实测数据分析

在盾构下穿过程中，随着切口位置的变化，双圆隧道上、下行线所受的扰动呈现非对称且不断变化的特性，导致上、下行线隧道结构的变形及空间位置分布具有明显差异性。

地铁双圆隧道结构内上、下行线之间的差异沉降Δ引起的双圆隧道横断面扭转角

α=arcsin (Δ/S)。

(1)

式中：S为双圆隧道圆心距；Δ=Δ1-Δ2，Δ1为地铁双圆隧道下行线竖向变形，Δ2为地铁双圆隧道上行线竖向变形。

由于扭转角α沿着双圆隧道纵向存在差异，将引起隧道纵向相对扭转

θ=Δα/l=(α1-α2)/l。

(2)

式中：α1、α2是隧道任意2个横断面的扭转角；l是这2个横断面沿隧道纵向的距离。

双圆隧道纵横向变形如图4所示。

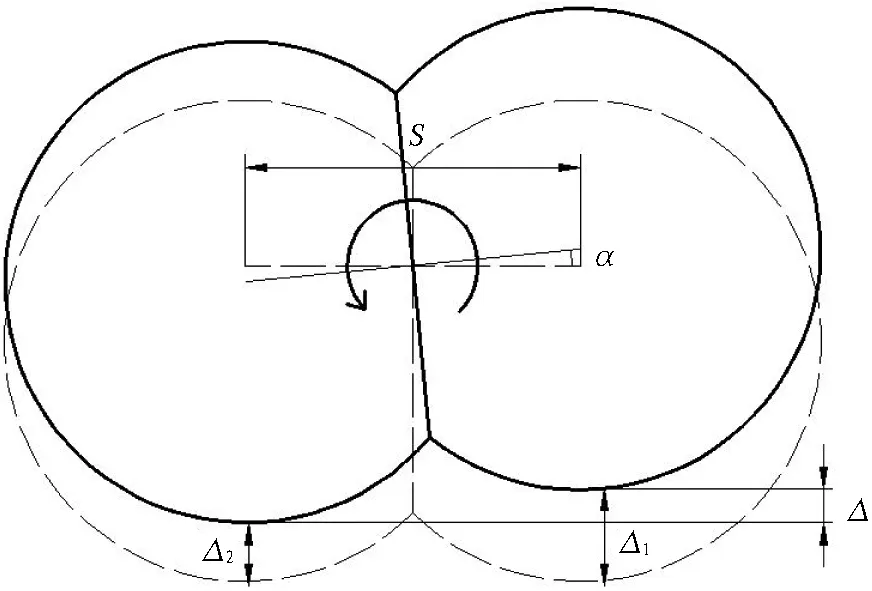
(a) 横断面扭转变形图

3.1 双圆隧道纵向隆沉位移变化规律分析

3.1.1 双圆隧道纵向隆沉分析

本文选取盾构不同切口位置时双圆隧道的纵向变形分布曲线的数据，分析盾构2次穿越时双圆隧道竖向位移变化规律(见图5-8)。

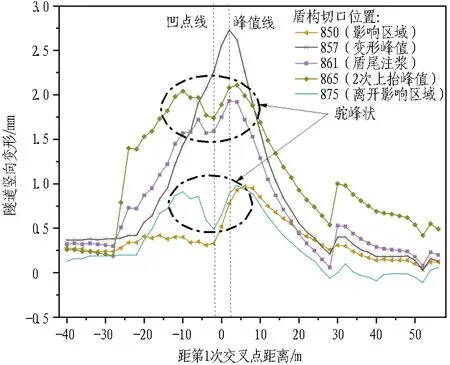
图5 第1次穿越时双圆隧道(下行线)纵向隆沉分布曲线Fig.5 Longitudinal settlement distribution curves of DOT tunnel (downline) during first undercrossing

图6 第1次穿越时双圆隧道(上行线)纵向隆沉分布曲线 Fig.6 Longitudinal settlement distribution curves of DOT tunnel (upline) during first undercrossing

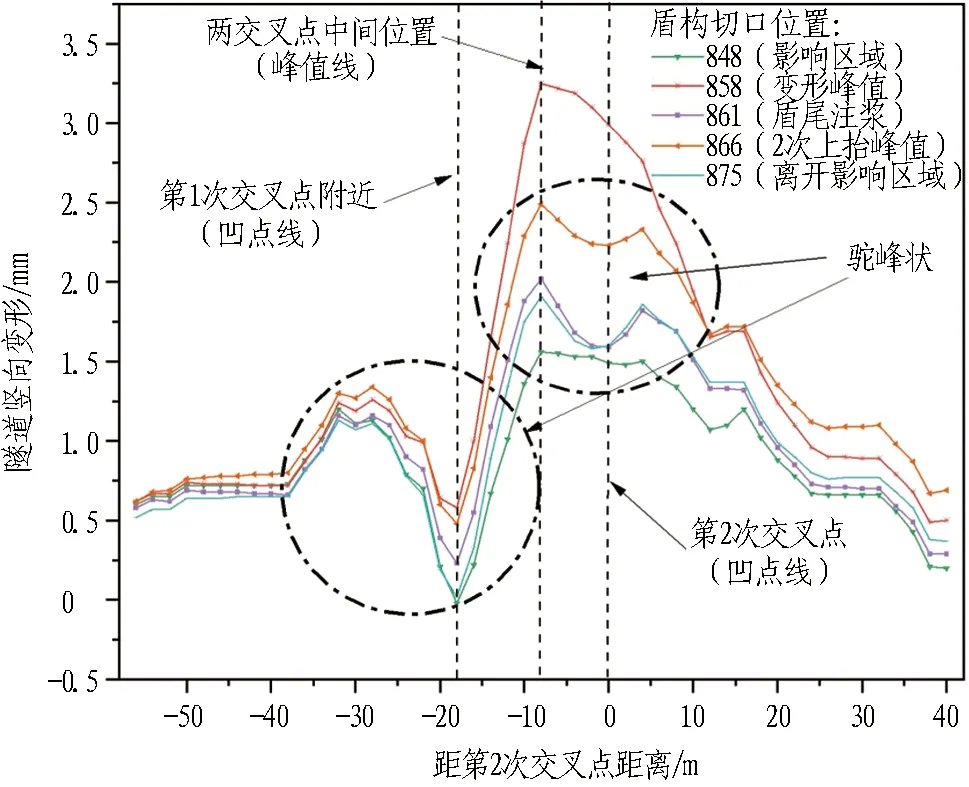
图7 第2次穿越时双圆隧道(下行线)纵向隆沉分布曲线Fig.7 Longitudinal settlement distribution curves of DOT tunnel (downline) during second undercrossing

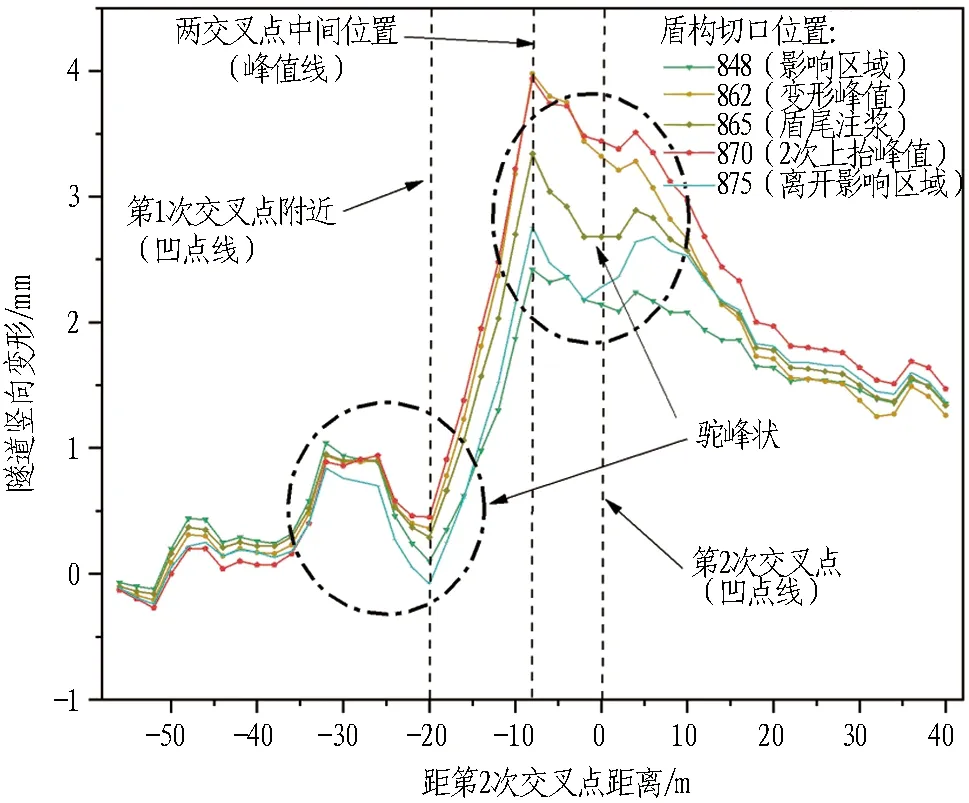
图8 第2次穿越时双圆隧道(上行线)纵向隆沉分布曲线Fig.8 Longitudinal settlement distribution curves of DOT tunnel (upline) during second undercrossing

3.1.1.1 双圆隧道纵向隆沉变化曲线分析

由图5-8可知：1)2次穿越过程中双圆隧道竖向位移主要以隆起为主，第1次穿越隆起覆盖范围约4D(D为盾构直径)，第2次穿越隆起范围有所增大，可达约6D，2次穿越后在交叉点附近局部都呈现"驼峰状"分布，覆盖范围约2D；2)第1次穿越，隆起变形主要发生在盾构切口到达地铁双圆隧道边缘至盾尾离开双圆隧道1D范围内，最大隆起位置发生在双圆隧道地铁线与盾构掘进轴线交叉处；3)在第2次穿越中，隆起量主要发生在盾构切口进入双圆隧道前约0.5D的距离至盾尾推出双圆隧道1D的范围，比第1次穿越变形时间延长，最大隆起位置出现在沿双圆隧道纵向与盾构轴线两交叉点的中间位置，表明2次穿越叠加效应明显。

3.1.1.2 双圆隧道纵向隆沉变化分析

对比前后2次穿越的隧道竖向位移发现：1)双圆隧道上(下)行线最大隆起出现的时间均在盾构切口离开上(下)行线1D，盾尾到达上(下)行线前约0.5D时。2)在盾构切口离开上(下)行线1D后到盾尾到达上(下)行线前的掘进过程中，隧道隆起变形表现出回落，该阶段隧道下方开始管片拼装，表明管片拼装阶段形成正地层损失，引起双圆隧道沉降。3)盾尾到达上(下)行线时，由于受到盾尾注浆的影响，双圆隧道上(下)行线变形开始出现2次上抬，至盾尾离开双圆隧道上(下)行线约1D的距离时，上(下)行线变形才再次回落，表明穿越施工对周围土体扰动造成的隆起存在滞后性。4)由于第1次穿越后隧道隆起未恢复，同时叠合第2次穿越的影响，第2次穿越时双圆隧道隆起量明显大于第1次穿越。对比2次穿越隧道变形的最大净隆起值，第1次穿越最大净隆起值约2.7 mm，第2次穿越最大净隆起值约2.1 mm，较第1次穿越减小22.2%。5)第1次盾构穿越中，变形曲线基本呈正态分布，盾构穿越后，交叉点附近变形曲线呈现"驼峰状"分布；第2次盾构穿越中，第1次交叉点附近变形曲线始终呈现"驼峰状"分布，使得变形曲线呈现双"驼峰"分布，穿越后，第2次交叉点附近同样呈现"驼峰状"分布，曲线呈现三"驼峰"分布。

3.1.2 双圆隧道纵向隆沉变化曲线特征指标

2次盾构下穿过程中，地铁双圆隧道均出现明显的纵向不均匀沉降。在穿越的整个过程中，地铁双圆隧道纵向不均匀变形≤5 mm，隧道纵向曲率半径≥15 000 m，相对变曲≤1/2 500。由于2次扰动影响，在第2次穿越过程中，隧道最大沉降明显增大，最小曲率半径减小，相对变曲增大。在盾构穿越各阶段中，隧道最大不均匀变形、最小曲率半径和相对变曲等如表3所示。

2次盾构穿越施工过程中，横断面(沿运营地铁双圆隧道纵向)沉降槽均体现为全部隆起，由盾构盾尾注浆挤压及正面挤压等引起的负地层损失所主导，第1次穿越隆起沿纵向分布基本服从正态分布。各阶段曲线的特征值和正态拟合结果如表3所示。

表3 双圆隧道地铁线纵向变形特征值和变形曲线正态拟合结果Table 3 Characteristic values of longitudinal deformation of DOT tunnel and normal fitting results of deformation curves

地铁双圆隧道纵向变形分布曲线和正态分布拟合曲线的对比结果如图9所示。

图9中正态分布拟合曲线公式为

(3)

式中：Smax为隧道最大隆起变形;x为沿隧道纵向任一点到最大隆起点的距离;i1为正态分布函数反弯点至最大隆起点的距离。

由表3和图9可以看出：1)在盾构穿越各阶段中，地层损失均为负地层损失，且地层损失率控制为 -0.18%～-0.62%，隧道绝对隆起量≤5 mm，第2次穿越影响区域大于第1次穿越影响区域，影响范围超过4D，可达约6D；2)第1 次穿越时隧道变形曲线和正态公式曲线拟合较好，两者拟合优度可达0.98，在首次穿越过程中可用正态分布公式预测隧道纵向变形规律；3)第2次穿越时，双圆隧道最大隆起点发生在两交叉点中间位置，变形曲线在第1次交叉点附近测点始终呈现"驼峰状"分布，该变形主要原因是地层损失的正地层损失率与盾尾注浆等引起的负地层损失率的叠加，虽然在盾尾注浆挤压及正面挤压等因素引起的负地层损失的作用下，隧道变形呈现整体隆起的状态，但是在盾构隧道中心附近地层损失导致的沉降变化更为剧烈，因此变形曲线呈现特殊的"驼峰状"分布。

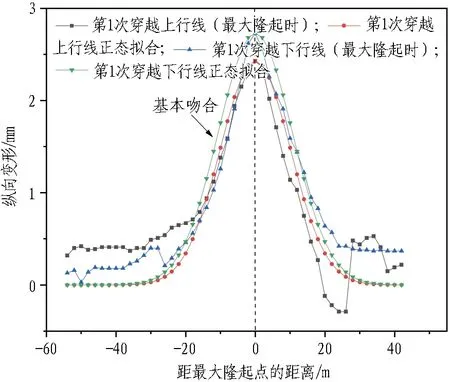
(a) 第1次穿越

3.2 双圆隧道扭转变形规律分析

3.2.1 双圆隧道断面扭转变化分析

选取穿越交叉点位置的横断面分析双圆隧道扭转随盾构穿越工况的变形规律，其中扭转角变化曲线及各阶段双圆隧道扭转变形状态如图10和表4所示。

3.2.1.1 双圆隧道断面扭转变化曲线分析

由图10和表4可以得出如下结论：

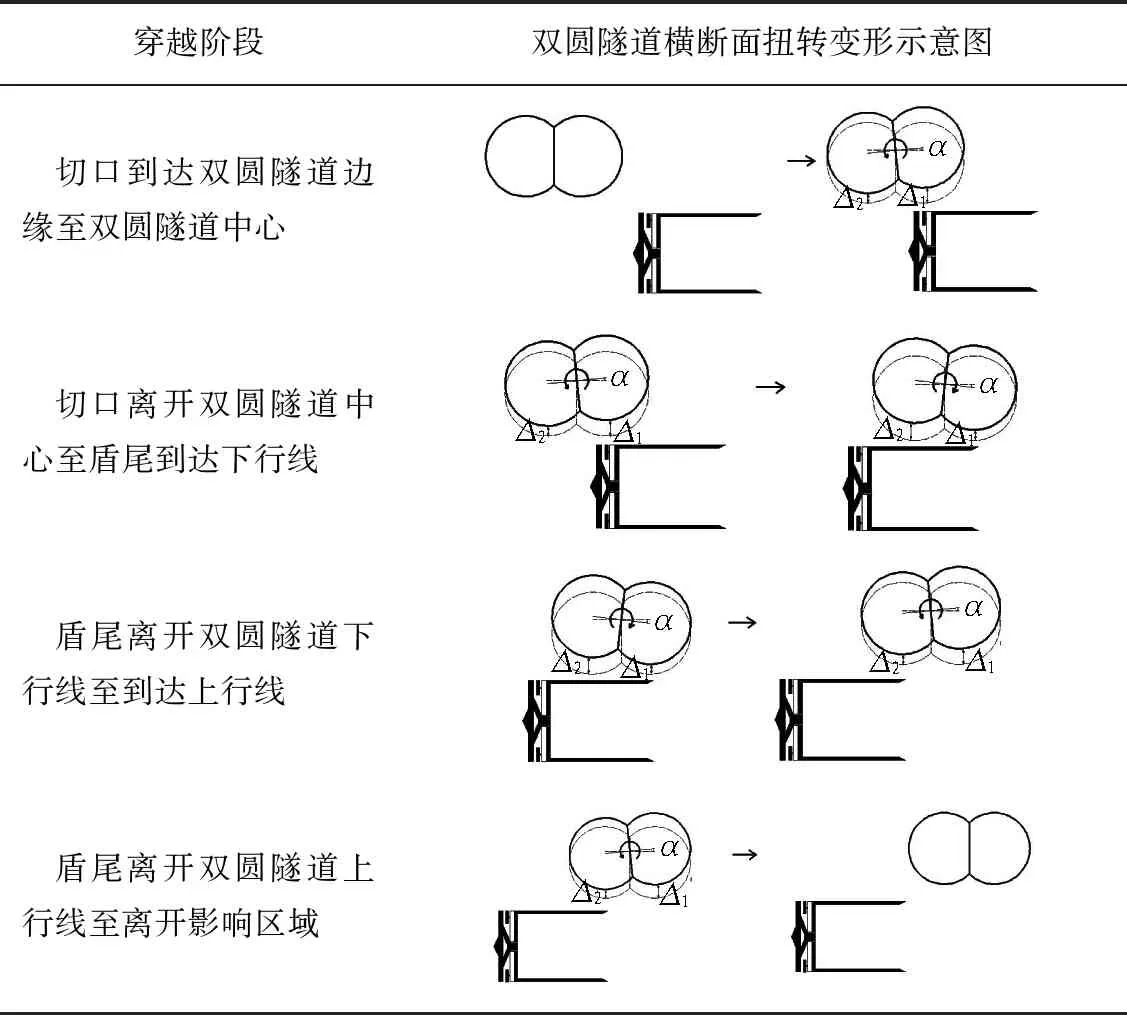
表4 双圆隧道各阶段断面扭转变形状态Table 4 Displacement of DOT tunnel in each stage

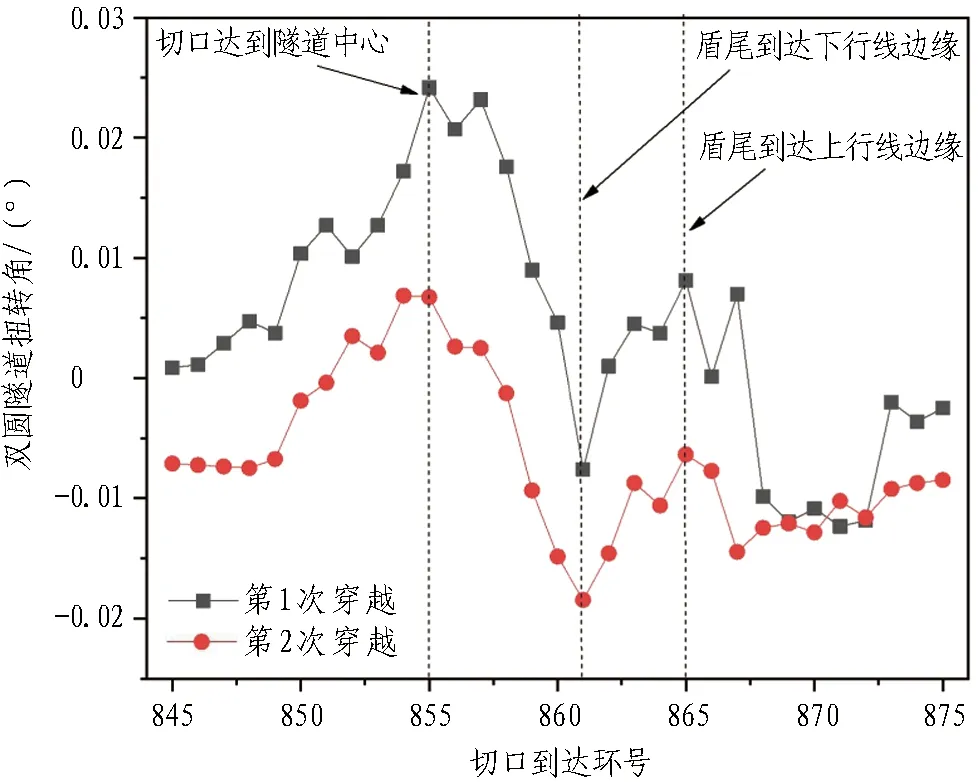
图10 双圆隧道扭转变形随切口位置变化曲线Fig.10 Torsional deformation of DOT tunnel varies with location of incision

1)第1次穿越时，当盾构切口到达隧道边缘时，双圆隧道上、下行线差异变形开始出现，扭转角出现增大的趋势，表明靠近切口的下行线变形大于远端的上行线变形，当切口到达隧道中心时，扭转角达到峰值约0.024°；随后扭转角开始减小，当盾构盾尾到达双圆隧道下行线时，由于受到盾尾注浆的影响，隧道扭转角曲线出现拐弯点，扭转角达到谷值约-0.008°。盾尾离开下行线下方后，开始向0°值波动。之后由于盾尾到达上行线，同样由于受到盾尾注浆的影响，隧道扭转角曲线再次出现拐弯点，而后隧道扭转角再次向0°值靠近。

2)第2次穿越时，双圆隧道扭转角在盾构切口从隧道边缘到隧道中心的范围内逐渐增大，并在切口到达隧道中心时达到最大值约0.007°。随着盾构盾尾靠近双圆隧道下行线，扭转角开始减小，并在盾构盾尾到达下行线时，达到最小值约-0.018°。而后，扭转角向0°值附近波动，期间由于受盾尾到达上行线同步注浆的影响，曲线再次出现拐弯点，扭转角呈波动变化。

3.2.1.2 双圆隧道断面扭转变形状态分析

在2次穿越过程中，隧道扭转角控制为-0.02°～0.03°，第2次穿越扭转角小于第1次穿越扭转角，变形虽小，但轨道横向倾斜(对应双圆隧道扭转)最大将近1/1 900，超过控制标准(1/2 500)，轨道横向倾斜难以达到控制要求。对比3.1章节中最大隆起时切口到达位置，扭转最不利出现时刻不同于双圆隧道最大变形出现时刻。双圆隧道扭转变形随切口位置呈波浪形动态变化，在穿越中出现2个最值：在盾构切口到达隧道中心时达到最大值，在盾构盾尾到达隧道下行线时出现最小值。这表明双圆隧道扭转变形与盾构切口和盾尾位置关系密切，盾尾注浆对双圆隧道扭转影响显著，将导致扭转变形发生变化。

3.2.2 双圆隧道扭转纵向分布分析

盾构2次穿越地铁双圆隧道扭转纵向分布曲线如图11和图12所示。

图11 第1次穿越地铁双圆隧道扭转纵向分布Fig.11 Longitudinal torsional deformation of DOT metro tunnel during first undercrossing

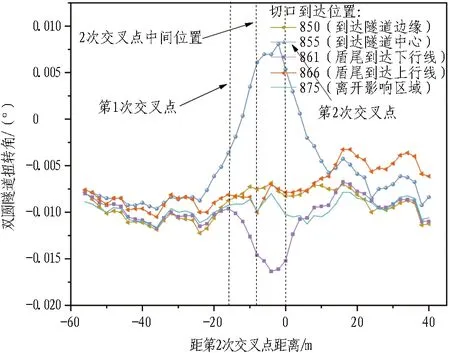
图12 第2次穿越地铁双圆隧道扭转纵向分布Fig.12 Longitudinal torsional deformation of DOT metro tunnel during second undercrossing

由图11和图12可以看出：1)第1次穿越时，最大扭转出现在地铁双圆隧道与盾构轴线交叉处；第2次穿越时出现在第2次交叉点位置附近，对比3.1章节中最大隆起位置，扭转最不利位置与最大隆沉位置发生了错位；扭转分布曲线均呈现中间大、两边小的分布，主要影响范围超过4D。2)2次盾构下穿过程中，双圆隧道均出现明显的纵向不均匀扭转。第1次穿越过程中，纵向不均匀扭转最大可达0.031°，相对扭转最大可达0.002 4°/m；第2次穿越过程中，纵向不均匀扭转最大可达0.025°，相对扭转最大可达0.001 9°/m。第2次穿越后的最大不均匀扭转及纵向相对扭转较第1次穿越分别减小19.4%和20.8%。

3.3 盾构穿越施工参数及工况的影响

3.3.1 盾构穿越施工参数分析

在盾构穿越期间，应尽可能减少盾构对地铁双圆隧道的扰动，选取合适的盾构施工参数，使盾构推进对地铁双圆隧道的影响控制在最小范围内。施工参数主要为土舱压力、推力、转矩、注浆压力等。施工参数随切口位置变化如图13所示。可以看出：1)在第1次穿越过程中，土舱压力控制为0.12～0.15 MPa，注浆压力为0.25～0.35 MPa，刀盘转矩控制为1 600～1 700 kN·m，推力为950～1 050 kN，推进速度为15～25 mm/min；2)第2次穿越时，盾构参数均有所提高，导致第2次穿越过程中隧道隆起累计变形增大，变形时间延长。

3.3.2 盾构穿越工况分析

穿越交叉点竖向位移随盾构切口位置变化曲线如图14所示。可以看出：1)2次穿越中，双圆隧道上(下)行线竖向位移均在盾构切口到达隧道边缘至离开上(下)行线1D的范围内迅速增加，该阶段上抬量占最大隆起量的90%以上，上抬速率约为0.32 mm/环；2)当盾构切口脱离隧道上(下)行线后，因受到盾尾注浆的影响，上(下)行线竖向位移出现2次上抬，注浆后的隧道隆起累计量可达到最大隆起量的70%以上；3)对比切口到达和盾尾注浆这2个阶段的累计隆起量，4个测点的比例为XU28∶SU28∶XU36∶SU36=1.35∶1.21∶1.22∶0.97；4)第2次穿越时，由于注浆压力的增大，出现盾尾注浆后隆起累计量大于切口到达时隆起量，表明盾尾注浆后导致的隧道累计变形可能会大于切口到达的变形，施工过程中应保证适当的注浆；5)当盾构离开隧道约1D距离时，测点普遍出现下沉，沉降速率约为0.1 mm/环。

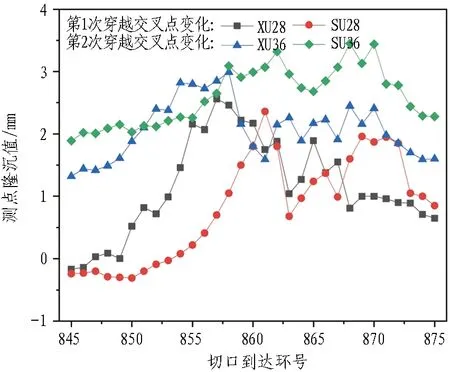
图14 穿越交叉点竖向位移随盾构切口位置变化曲线Fig.14 Vertical displacement of feature points varies with location of shield incision

4 结论与建议

1)盾构下穿双圆隧道引起的竖向变形主要为隆起变形，主要发生在盾构切口到达双圆隧道边缘至盾尾离开隧道1D的穿越时段。第2次穿越累计变形明显大于第1次穿越累计变形，且变形时间更长。

(a) 土舱压力变化

2)2次穿越引起的最大变形位置有所不同，第1次穿越在双圆隧道地铁线与盾构掘进轴线交叉处，隆起范围约为4D，第2次穿越在沿双圆隧道纵向两交叉点中间位置，隆起范围约为6D；穿越后，交叉点附近变形呈现"驼峰状"分布，对称中心位于2条隧道交叉处，影响范围约为2D。这种"驼峰状"隆起分布曲线是近年来软土地层中盾构下穿运营隧道中特有的现象，值得关注和研究。

3)双圆隧道扭转变形随切口位置呈波浪形动态变化，主要影响范围超过4D，对隧道环缝受力与变形十分不利，扭转变形引起的轨道变形也难于控制，因此在盾构穿越双圆隧道期间，应重点关注扭转变形的情况。双圆隧道断面最不利扭转出现时刻不同于隧道最大变形出现时刻，且扭转最不利位置与最大隆沉发生位置产生了错位。曲线拐弯点出现与切口位置、盾尾注浆位置密切相关，第2次穿越的隧道纵向最大不均匀扭转变形及纵向相对扭转较第1次穿越时分别减小19.4%和20.8%。

4)盾尾注浆对控制隧道竖向位移效果明显，但注浆后的隧道变形累计隆起量可能大于切口到达的隆起量，这将加剧双圆隧道的不均匀变形和扭转。建议采用适当注浆的方法，以避免出现过量注浆导致隧道隆起过大的情况。

盾构近距离施工对已运营双圆隧道的影响显著。考虑到双圆隧道变形与盾构切口和盾尾注浆位置密切相关，为保证运营隧道的安全，在穿越施工过程中应采取信息化检测、严格控制注浆等有效措施以保证工程顺利进行。本文通过实例分析，对双圆隧道穿越过程中的变形特征与变化规律进行总结，这对类似穿越工程以及双圆隧道结构的保护具有一定的借鉴意义。