考虑桩土相互作用的单管塔整体分析

史国富 屠海明 陈晨

(同济大学建筑设计研究院集团(有限)公司 上海200092)

引言

单管塔广泛应用于通信基站、输电塔、灯杆等高耸构筑物，其传统基础形式可分为独立基础、群桩承台基础两大类型。在软土地区，群桩承台基础得到了广泛的应用，其桩型常为钻孔灌注桩，采用四桩承台或三桩承台的形式。

近年来，随着征地难度的加大，对单管塔的基础占地面积提出了更高的要求，单桩基础单管塔逐渐兴起。按桩型种类可分为混凝土灌注桩、单管钢桩两种类型。单管钢桩的桩及塔体均可工厂预制，钢桩因具备无需养护、施工期短、造价低等优点得到了更为广泛的应用。

1 单管塔及桩基础设计现状

传统分析方法将上部结构和基础分别考虑、分开计算，不考虑上部结构、基础、土体的相互作用和影响。对于群桩承台基础，基础顶面单管塔底部传递的弯矩、剪力通过承台转换为单桩的抗压和抗拔，桩体受力模式为桩竖向承载力，其刚度大，基础顶部可作为单管塔的嵌固端，这种上部结构和基础分开计算的方法是符合工程设计精度的。

然而，单桩基础由于其水平刚度、抗弯刚度的限制，仅靠周围土体和桩身刚度并不能对单管塔底部形成嵌固，单桩基础的位移、转角均会对单管塔的结构特性、整体性能带来一定的影响，需考虑将上部结构及单桩基础整体分析。

2 单管塔单桩基础分析方法

单管塔单桩基础主要承受水平力和弯矩，与一般承受水平力的单桩不同，其顶部弯矩往往较大。单桩水平承载力不仅取决于桩侧土质的横向抗力，还取决于桩的弯曲刚度、强度、桩顶约束条件等因素。目前单桩水平承载力计算方法主要有理论计算和数值计算方法。理论计算方法主要有极限地基反力法、线性弹性地基反力法、非线性弹性地基反力法以及弹塑性地基反力法。线性弹性地基反力法假定桩基础周围土为Winkler离散线性弹簧，不考虑基础与土之间的粘着力和摩阻力。根据地基的基床系数假定不同，又分为张有龄法、C法、K法、m法等[1，2]。《建筑桩基技术规范》(JGJ94—2008)[3]中采用基于线性弹性地基反力的m法计算单桩水平承载力，基床系数随深度线性增加。

本文水平向桩土之间相互作用采用m法，整体分析计算采用有限单元法。将水平向土体对桩身之间的作用离散为线性弹簧，弹簧刚度采用m值进行计算，整体分析时作为弹簧支座约束于桩体。弹簧刚度计算公式[1]如下:

式中:Ki为土体集中弹簧刚度，kN/m；m为桩侧土水平抗力系数的比例系数，kN/m4；b0为桩身计算宽度，m；zi为自地面至第i个集中弹簧的距离，m；l为桩单元划分长度，m。

3 工程实例

3.1 工程概况

单管通信塔上部结构为插接外爬单管塔，塔高40m，截面为正十八边形，塔体为锥形渐变结构，自下而上外接圆直径为1.12m～0.45m，筒体壁厚10mm～6mm；基础采用等直径钢管单桩基础，钢桩直径1.25m，壁厚12mm，桩长10m。结构设计基本风压0.45kN/m2，地貌类别B类，共设置4层天线，每层设置3副天线支架，每幅天线挡风面积不超过0.6m2，RRU挡风面积不超过0.2m2。单管塔及基础立面如图1所示。

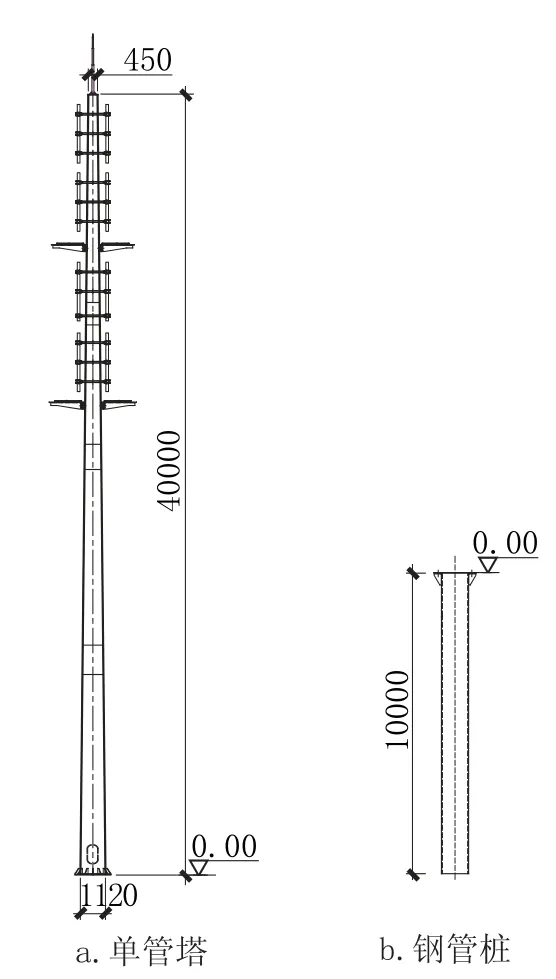
图1 单管塔及桩基础立面Fig.1 Elevation view of monopole

拟建场地地形较平缓，地貌单元为冲海积平原。地基岩土分为2个工程地质层，4个亚层，主要土层参数见表1。

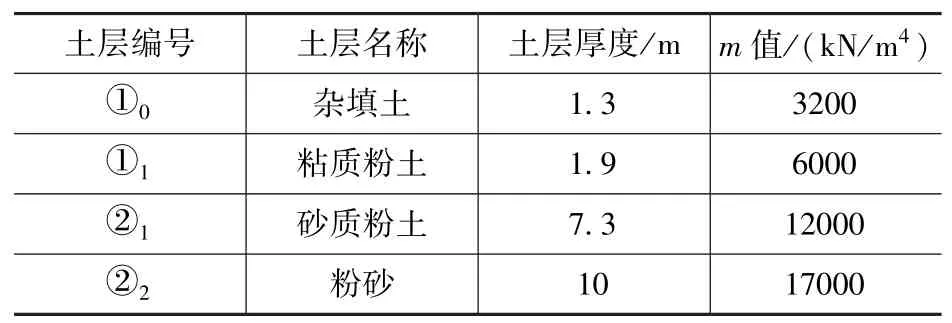
表1 土层参数Tab.1 Soil layer parameters

3.2 整体分析法和独立分析法计算比较

整体分析时采用结构分析软件SAP2000，塔体采用变截面锥形梁单元，桩土相互作用采用弹簧支座模拟，弹簧刚度计算采用公式(1)。单管塔静力分析考虑P-△效应进行非线性分析。

独立模型桩基采用《建筑桩基技术规范》[3]附录C的计算规定，采用单桩基础的计算公式，计算步骤详见规范表C.0.3-1，系数查表C.0.3-4。

两种计算方法主要计算结果见表2。

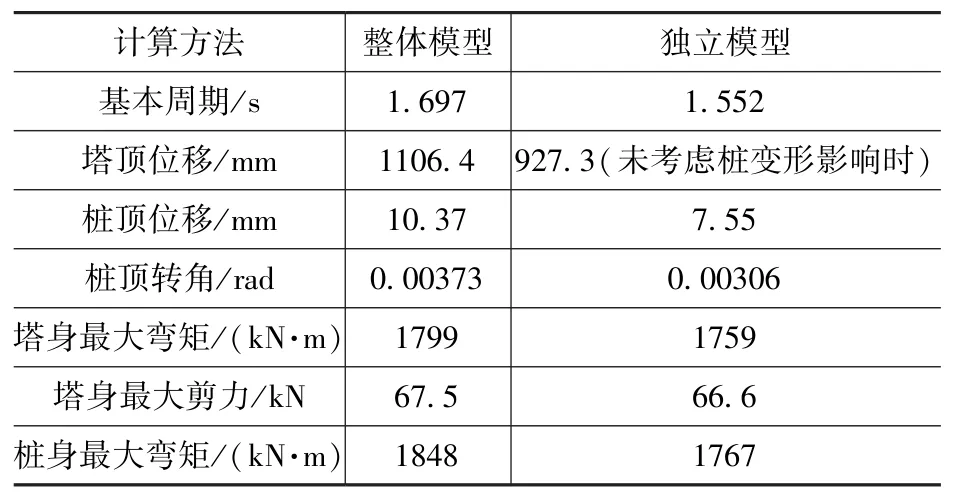
表2 两种计算方法的主要计算结果Tab.2 The main results of the two calculation methods

二者塔顶位移相差较大的主要原因在于独立分析法是基于基础对上部结构的嵌固的假定，不考虑桩顶位移和转角对上部结构的影响。对于单管塔而言，桩顶的转角会造成塔顶较大的水平位移，二者关系可用近似公式表达为:

式中:Δ为桩顶转角引起的塔顶位移，mm；θ为桩顶转角，rad；H为塔高，mm。

故当采用独立分析方法时，考虑桩顶变形的单管塔塔顶位移近似计算公式应为:

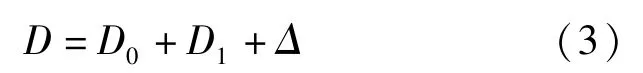
式中:D0为独立分析时塔顶位移；D1为桩顶位移。

因此考虑桩顶变形时单管塔塔顶位移为D=927.3+7.55+0.00306×40000=1057.2mm。

由表2可知，整体分析模型较独立分析模型结构基本周期增大9.34%，塔顶位移增大4.65%，桩顶位移增大37.3%，桩顶转角增大21.9%；整体指标均有较大的增加，其影响不可忽视，桩顶变形差异较大的原因主要是规范计算方法与软件有限元数值计算方法的差异所致，规范方法计算结果偏小。整体模型较独立模型塔身弯矩增大2.27%，桩身最大弯矩增大4.58%，对结构内力相对而言影响较小。

在实际设计过程中，采用独立分析法进行上部结构设计时，应考虑不同的基础形式对上部结构的影响，尤其是对同一种塔型必须充分考虑桩顶变形对整体结构顶部位移的影响，对同一种塔型的应用要结合基础形式综合考虑其顶部位移指标。

4 增大钢管单桩基础刚度措施探讨

当塔顶位移不满足规范要求时可通过增大上部或下部结构刚度来实现，本文仅讨论增大下部结构刚度。上述分析表明，单管钢桩基础顶部的转角对结构的顶部位移影响较大。这主要是单桩基础抗弯刚度较弱及桩顶弯矩较大所致，应采取措施增大桩身抗弯刚度以减小桩顶转角，进而减小对单管塔顶部位移的影响。常规方法可通过增大钢桩钢管直径、壁厚等来实现，但这些方法均会较大地增加基础造价，更好的方式应是钢桩用钢量不变的前提下，采用钢桩内部填充混凝土，以此方法增加桩身刚度。本文探讨采用等直径钢-混凝土和变直径钢-混凝土复合截面桩基两种形式。在保持用桩基钢量不变的情况下，变直径锥形钢桩顶部直径采用1.6m，底部直径为0.9m，并对混凝土不同浇筑高度时分别建模整体分析。计算桩身混凝土填充高度(距桩顶)变化时对结构整体性能的影响，主要计算结果如图2所示。

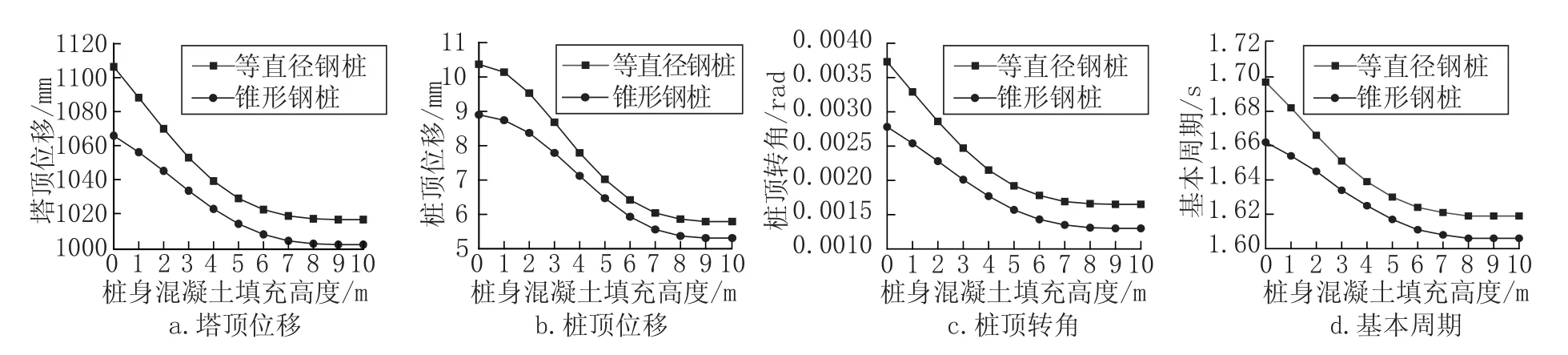
图2 混凝土不同填充高度对结构的影响Fig.2 Effect on structure of different filling height in steel pile

由图2可知，钢-混凝土复合截面桩基可有效减小塔顶位移和桩顶变形，比较而言变直径钢-混凝土复合截面桩基效果更为显著，塔顶位移最大可减少9.5%。从图2a、b、c中位移、转角的变化趋势看，当混凝土填充高度(距桩顶距离)大于主要影响深度hm=2(d+1)[3](d为桩径)时，其位移及转角衰减趋于平缓。因此在实际工程中，可采取钢桩内部混凝土的填充高度为影响深度值以节约造价。

5 结语

1.采用单管钢桩基础时，对于以位移控制为主的单管塔，须考虑桩土共同作用，采用整体模型分析，考虑基础刚度对结构整体性能的影响。

2.当采用传统独立式方法进行分析时，应考虑桩顶变形对结构的影响，可采用近似公式计算塔顶位移。

3.针对单桩基础抗弯刚度较弱的特点，应采用必要的措施以增大桩身刚度，控制桩顶转角变形，分析表明变直径钢-混凝土复合截面是经济有效的方式。

4.由于变直径锥形钢桩其桩身刚度随填充混凝土高度变化，通过数值计算得到填充高度以主要影响深度为佳。