在动态几何实验教学中培养学生的数学直觉
王思敏 周松林 林宇杰
([1]广西师范大学数学与统计学院 广西·桂林 541004;[2]桂林市第一中学 广西·桂林 541004)
数学直觉是对于数学对象事物(结构及其关系)的某种直接领悟或洞察。在传统数学教学中,培养学生的数学直觉常常缺失“显微镜”和“放大镜”等技术的支持。而动态数学技术具有数学化、视觉化、动态化呈现数学对象与思维的功能,应用动态数学技术是数学实验教学中培养学生数学直觉的利器。本文尝试探讨在几何实验教学中利用动态数学技术培养学生数学直觉的一些思考。
1 在平面几何实验教学中,精准绘测,捕捉数学直觉
在传统教学中,学生无法测量数学对象的长度、面积等数值,因此在平面几何学习中易错失许多“特殊”的数量关系,难以捕捉数学直觉。在基于动态数学软件的实验教学中,可以选择“测量”功能,任意测量数学对象的数值,通过变化数值,指引学生捕捉数学直觉,助力学生直观感知数据背后的规律。
案例一:从勾股定理到余弦定理。
勾股定理是最基本的几何定理,在常规教学中,教师通过设计案例来引导学生发现这一定理。但若不通过预先设计好的案例,能否让学生自己发现这一规律呢?从动态数形结合来看,利用动态数学技术测量和拖拽功能,有助于验证勾股定理在任意三角形中都成立。借用这种数学直觉,不妨测量非直角三角形的边长。
通过测量三角形多边长度,如图1,在△ABC中,AD⊥BC,观察可得。为什么会出现这种情况呢?不难发现AB、BD分别是Rt△ABD的斜边和直角边;AC、DC分别是Rt△ADC的斜边和直角边,根据勾股定理有上述等式成立。
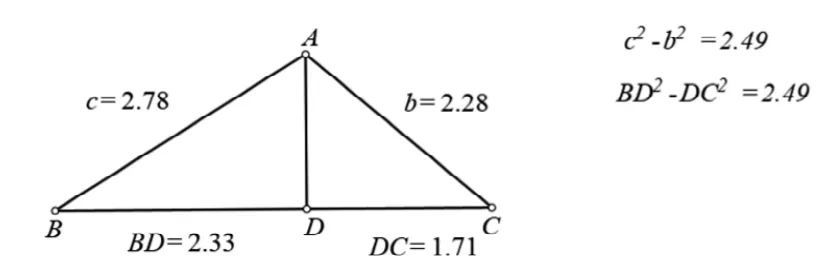
图1
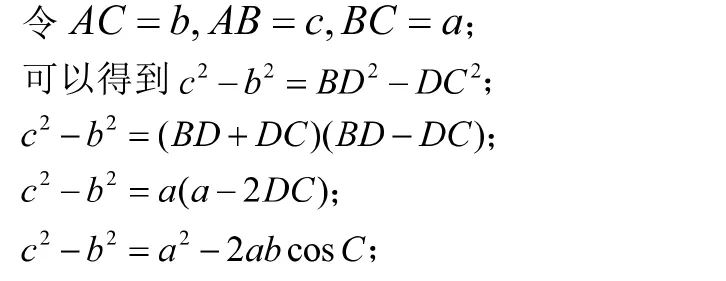
即证余弦定理。相较于传统教学中用向量推导余弦定理的方法,此种推导方式显示出其巧妙性:在实验教学中,学生使用动态数学软件测量功能发现等量关系藉此捕捉数学直觉“类似勾股定理”,将其转化为△ABC三边长的数量关系。再按平方差公式展开并用进行等量代换,最终实现余弦定理的推导。
2 多元表征立体几何,激发数学直觉
教材中立体几何的公理或定理大都直接给出,但很难让人直观感知或想象。在动态数学实验教学中,可以任意切换三维与二维图形,实现多视角观察立体图形的结构与构成要素;通过二维、三维图象、动画演示、颜色闪动、文字解说、语言互动等多元方式表征,一方面降低了空间想象上的负荷,另一方面也激发学生对学习对象的兴趣,有助于实现“授人以鱼的同时,更授人以渔与欲”。
案例二:从祖暅原理到空间几何体的面积。
《九章算术》中提到祖暅在求球体积时,使用的原理是:“幂势既同,则积不容异”。“幂”是截面积,“势”是立体的高。意思是两个同高的几何体,如在等高处的截面积都相等,则它们的体积相等。祖暅原理可用于推导球的体积公式,类似于微元法分割。但这个原理以静态的图像演示相对困难,学生难以发现同一平面切面的圆环与圆的面积相同。
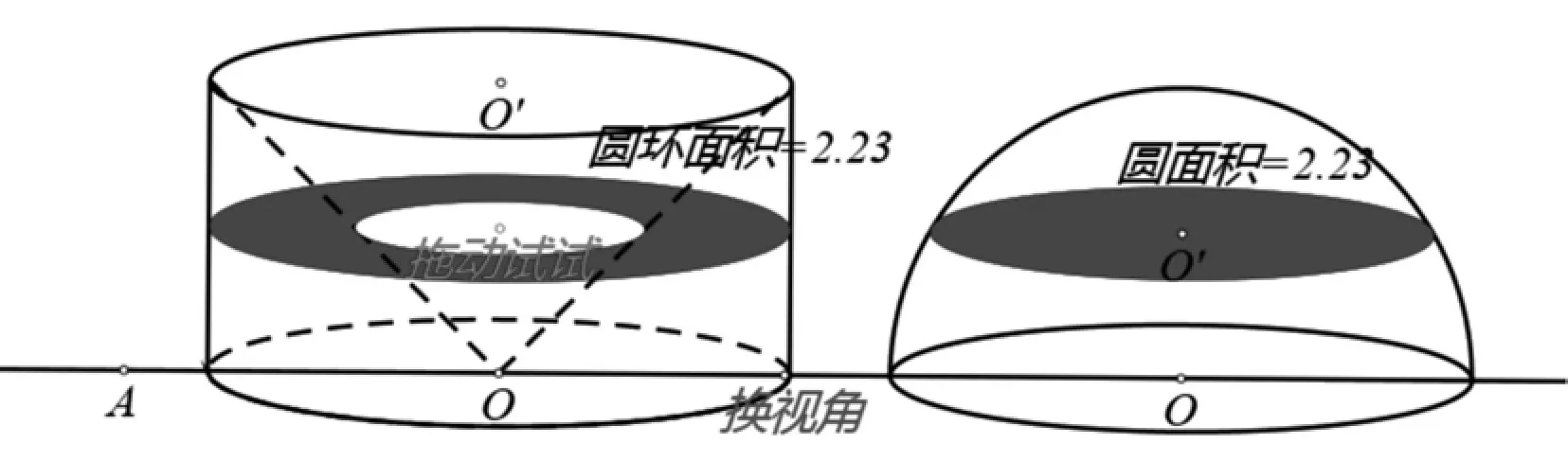
图2
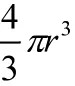
3 动态探究解析几何,训练数学直觉
解析几何中的动态几何问题是教学的重难点,传统教学中的“化动为静”方法将运动的动图裁剪成单帧的静态图片,对学生的直观感知能力要求较高。相比而言,动态数学实验教学重现数学图形运动过程,学生可以随时按下暂停键观察。这样在学生脑海中便不是截断的图片,而是连贯的动图,在动态中解决动态问题,相对符合学生的认知发展规律。
这是一道考查圆与抛物线位置关系的练习题,不难看出圆的圆心是(a,0),半径恒为1。常规做法是将抛物线方程代入到圆的方程中,可以得到
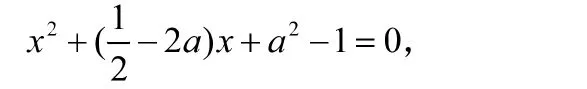
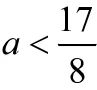

图3
究其出错缘由,学生在日常学习中过多依赖代数,缺乏数形结合的思想。没有经过几何直观,便无法在脑海中形成清晰表象,也就无法解决由于认知偏差所带来的失误。动态数学软件的作图、测量、跟踪等功能可以帮助学生理解图形,建立图形的数量关系,增强直观想象能力。
4 结语
日本数学家小平邦彦说:“数学就是一种感觉”。动态数学技术在探索定理、证明命题、解题教学中的合理使用,能有效培养数学直觉。值得说明的是,即便动态数学实验教学能够测量并发现一些数学事实,但它不能代替逻辑推理的归纳演绎。在一定程度上,动态数学技术有助于发现和探索数学规律,培养数学直觉,但直觉作为一种非理性的思维,具有一定主观性,需要辩证对待。

